自由空间中天线近区场的类消失态超光速现象
2013-03-13黄志洵
黄志洵
(中国传媒大学信息工程学院,北京 100024)
1 前言
2000年笔者曾发表一篇论文,题为“对开放空间中微波异常传播现象的探讨”[1],它被收入于2002年出版的《超光速研究新进展》书中[2]。文章讨论了20世纪90年代国际上报道的几例超光速实验,例如在喇叭天线的辐射近场区观察到“微波波速超过自由空间中电磁波本征速度c”的现象。文章说,这在文献中被称为微波传播中的异常脉冲延时,目前对其机理尚不甚清楚。近年来(2009-2012年),又有关于自由空间中电磁波超光速传播的论文出现,有理论工作也有实验工作。因此有必要重新论述这一课题,以期获得更全面、更清楚的认识。
过去的许多超光速实验论文,或利用反常色散(anomalous dispersion)效应,或利用量子隧穿(quantum tunneling)现象,这都涉及某种特殊制备的媒质或器件。现在讨论的现象则不用这些东西,仅在自由空间观察电磁波传播,超光速(甚至负波速)现象也出现了——这里所说是在天线的近区(near region)所呈现的奇妙特性。我们认为这是由一种可称为类消失态(evanescent-state like)的电磁状态所造成的;与此相联系的是,不应忽略在求解Maxwell方程时与推迟解同时出现的超前解(advanced solution),实验中即使出现负速度也可以解释。
2 时间对称性问题与超前波
众所周知,对时间、空间的看法,在Newton力学(Newton Mechanics,NM)中和相对论力学(SR和GR)中是不相同的。NM的时间观可简洁地概括为:时间连续而均匀地单向流逝,并且无始无终,是一种不依赖于人类的客观存在。我们认为这可以作为讨论一般物理问题的出发点。有一个名词叫时间箭头(time’s arrow),其热力学含意是表示闭合系统中无序度(熵)总是随时间增加而增大;心理学含意是人能记住的只是过去而不是未来,事件总是从过去到现在再到将来;宇宙学含意是宇宙不断膨胀而非不断收缩。不过,自然科学的理论发展告诉我们,科学定律对时间是往前走还是向后退是相同的,例如一些物理学方程具有的特征为:以(-t)代替t后方程不变。因此,不能由科学定律区分时间的方向(前进或后退)。上述情况说明,在做科学研究时不能忽略“时间对称性”的问题。
令人困惑之处在于,在真实的世界和生活中时间保持单向性。例如打碎茶杯或在碗中搅开生鸡蛋都很容易,反之如想使已粉碎的杯子复原或使已搅开的蛋液再成为最初的样子和结构,不仅困难之极甚至是不可能做到的事。但在科学方程中却不是这种情形,“过去到未来”与“未来到过去”是一样的;正如天文学家A.Eddington所形容:“没有路标显示这是一条单行道”。
必须考虑Maxwell方程组与时间的关系。空间中有源(电荷源或电流源)时的Helmholtz方程是非齐次的[3]:


1939年至1941年间,著名物理学家R.Feynman和他的老师J.Wheeler共同提出电动力学吸收者理论[4]。最初他们是研究粒子(例如电子)的相互作用问题,却发现自己陷入了过去、未来的困难中。为使理论体现出对称,必须引入超前场(advanced field)概念;这也称为超前效应(advanced effect)。这种不是由源向外辐射出去、而是向内移动的波,看起来其运动是时间倒转的,总给人以奇怪的印象。Wheeler还考虑了迟滞波与超前波互相结合(相消)问题,以及反作用到源的能量问题。尽管后来他们发表了论文,但在自那以后的几十年中,超前波的观念从未受到科学界的重视。
3 天线场分区理论
所谓小电偶极子(basic electric dipole)是假定其长度远小于波长(l≪λ),线上电流为同相、等幅分布的线天线。把它放在球坐标的中心(图1),则它产生的各场分量为:
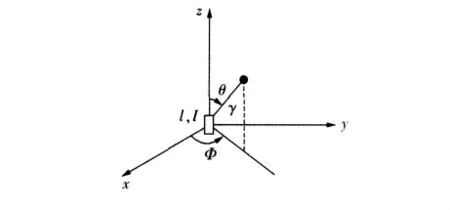
图1 小电偶极子和球坐标

式中k0=ω/c是波数(c是真空中光速);M是偶极矩(dipole moment),等于电流I与长度l的积,故单位为A·m;因此,我们有

第一项是静电场,理论上是由偶极子两端电荷所产生;把它写作Es(下标S代表static),则有

可见,场强随r增大减小很快,这还表示对于近处静电场强度大。上式表明|ES|∝ω-1,故在高频该分量很小。
第二项是感应场,理论上是由偶极子电流所产生;把它写作EI(下标I代表Induction),则有

故场强随r增大的减小也较快,而此项场分量与频率无关。以上两项总称为,表示其对天线(电偶极子)的依附性质。
第三项是辐射场,用表示ER(下标R代表Radiation):

可见,当r增大时辐射场分量的减小甚慢;ER∝ω表示在高频段仍能保有其强度。
我们注意到,当

上述三个分量相等:

这是非常有趣的;这个特定的距离是与频率有关的量,例如当 f=500Hz=100km;f=0.5MHz=100m;等等。这一情况可用图2表示其大概。当r>1km,已可仅仅考虑辐射场分量——假如我们只注意几百千赫的话。

图2 不同类型的场强变化
关于天线场区划分,先讨论小辐射器(电流元、小型线天线)的情况,其尺寸小于波长。在它的周围,场区可划分为(参看图2):
①静电场区(Electrostatic field region),条件是r≪λ/2π;
②感应场区(Induction field region),条件是r处在λ/2π附近;
③辐射场区(Radiation field region),条件是r≫λ/2π;
前两者总称为近场区,后者又称为远场区。
考虑到

式中Z00是真空波阻抗,亦即自由空间本征阻抗(intrinsic impedance of free space)。这个值常取120π(精确值是376.62Ω);为了与老的写法相一致,我们就取这个不精确值,可得

所以前面的公式实际上可写作:

考虑e-jk0r≅1的情况;这表示电磁理论中的推迟势(也叫滞后势)方程,近似为Poisson方程。就是说,如果k0r≪1,靠近天线的场满足Poisson方程。物理概念是:即使电磁场随时间t迅变,靠近场源的场分布仍遵循稳态场规律。取k0r≪1,亦即r≪λ/2π时,可得

可见,在距天线近处,Er与Eθ同相,它们与 Hφ有(-π/2)的相位差,这意味着能量在偶极子与空间场之间往返,但平均值为零(因平均Poynting矢为零)。在天线与周围媒质之间有能量的脉动,这正是感应场的基本特征之一。
总之,感应场的情况不仅与场源性质有关,还取决于环境因素。对于一个任意的场源,感应场结构分布很复杂。它的场阻抗与场源相关,是频率的函数(不能把Z00当作感应场的波阻抗)。

现在考虑远区(r≫λ/2π);这时项e-jk0r不能忽略,而 Er≅0,故有Eθ与Hφ同相,两者乘积为正(Poynting矢方向总向外)。这是辐射场,它近似于球面波。应当说明,虽然在近区辐射场远小于感应场,但它仍比远区的辐射场大得多。
然后讨论大辐射器天线场区域划分。大辐射器(如大型面天线)的尺寸远大于波长λ,感应场一词在这里没有意义,只是把某些与rn(n>1)成反比的项叫做近场项(near-field terms)。文献的许多讨论是针对微波的。广义的天线应包括馈源(feed)和辐射元件(radiating elements)。例如,微波传输线的主要形式——波导,为了保证单模传输,横向尺寸有所限制:对于圆波导,要求内径满足D<λ/1.31;对于矩形波导,要求宽边内尺寸满足a<λ。如果要从传输线过渡到辐射元件,必须使横向尺寸逐步扩大,成为喇叭状、抛物面状,如图3所示。波导壁与天线面都是金属质,它成为“内场”(分为单模区和多模区)和“外场”的边界,天线的最大尺寸为D,在那里的场是口面场。外场区首先是(很近于口面场),是储能性质,范围是r<λ/2π时,近似r<λ/6。

图3 大辐射器的场区示意
一个基本的问题是:在一个等相面(equi-phase surface)上给定电场矢量、磁场矢量的值,如何决定另一特定点处的场矢量?Huygens-Fresnel原理给出

条件r>2D2/λ是远区场的下界(最小距离)。实际上,为了更好地符合平面波条件,可取数十倍D2/λ作为实用距离,即远大于2倍。故远场区是指r=2D2/λ~∞的区域。r<2D2/λ的范围都是近场区,表1中的“远区最小距离”就是“近区最大距离”。

表1 近区与远区的分界(大辐射器)
应当说明“Fresnel区”、“Fraunhofer区”的含意。A.J.Fresnel(1788-1827)是法国物理学家;所谓Fresnel衍射,是指光源在近处、在有限距离内形成的衍射图象。J.von Fraunhofer(1787-1826)是德国物理学家;所谓Fraunhofer衍射,是指光源在无限远处、屏幕在无限远处形成的衍射。如假定天线聚波束于无限远,也可把远场区叫做Fraunhofer区。
至于远区场,E和H之间无相位差,平均Poynting矢不为零。在这里,通常满足平面波条件;E/H比值恒定,测出了一个就知道另一个。令Pd为功率通量密度(power flux density),则有

式中E、H均为有效值;由于E/H=Z00,故有

又有

在 μ0、ε0均取精确值时,Z00=376.62Ω,故有

这些公式只能用于远区场。
4 天线近区场与消失场的比较研究
天线近区场具有复杂的结构,我们依然按照电小偶极子的情况而论述。在近区,场的物理特征使我们想起消失场(evanescent field)——一种广泛存在于各种情况下电磁的现象;故本文尝试对两者作比较研究。先看消失场,其物理特征如下[3]:
①迅速衰减的特性:按照e-αr的规律,场幅沿r方向迅速下降;衰减常数α越大下降越快。
②时间相位关系:电磁波的纯行波状态,电场与磁场的时间相位相同,即E→和H→的时间相位关系没有相差(夹角为零)。但在消失波(场)条件下,电场和磁场的时间相位相差π/2,即1/4周期。在TM模式时,磁场矢量超前;在TE模式时,电场矢量超前。Poynting矢瞬时值)或,在纯行波时为纯实数,在消失波(场)条件下为纯虚数。平均 Poynting 矢,即或在行波时不为零,代表实功率流;但在消失波(场)条件下为零。
③电抗性(储能性),以及电场、磁场的可分离性:以波导为例,当作传输线使用的传输波导,高频平均电能与高频平均磁能基本相同,即We≅Wm。但在截止波导中(消失态),TM模情况We>Wm;如f≪fc(fc是波导截止频率),则We≫Wm,波导中主要是电场,波阻抗Z0E≅jX0E,有点像电容器。反之,TE模情况 Wm> We;如 f≪fc,则 Wm≫We,波导中主要是磁场,Z0H≅jX0H,有点像电感。总之波阻抗都是电抗性,体现电能的储存或磁能的贮存。
④准恒定性或类稳性:准恒定场(quasi-steady field)即类稳场(quasi-static field),是变化缓慢(故电场与磁场相互作用较弱)的时变场。场的推迟势方程在时间导数项为零时得到Poisson方程,无源时进一步得到Laplace方程。正因为如此,对于消失态问题,例如对截止波导和截止衰减器的分析,可以用等效电路法(集总元件L、C组成的电路)去分析处理。
⑤大驻波特性:笔者早就指出,虽然传统上对消失场(器件如截止波导)可以按照电压波理论(即行波理论)描述,但也可按照另一理论体系即功率波理论(power-wave theory)描述[3]。如果硬要用前者,则会出现大的(或超大的)电压驻波比。从本质上讲,消失场(evanescent field)不是波,文献上常见的词消失波(evanescent wave)并不确切,因为它没有波动的进行。如一定要说它是波,那么也只是驻波(standing wave),即在原地振动的电磁现象。
独立撰写、主编或参编30余本专著或教材,已出版的主要著作有《证券史与证券税制研究》《德国财政税收制度研究》《财政与会计关系史比较研究》《中国财政通史——五代两宋》《财政源流关系研究》《中国财政通史(第十卷)中华人民共和国财政史》(下册)《代表谈财政》《代表谈审计》《中国公车改革之路》《社群运营》等,在《经济日报》(理论版)《人民日报》《财贸经济》《财政研究》《税务研究》等杂志发表论文70余篇。承担财政部、教育部、国家统计局等单位课题十余个。有十余篇文章或课题获奖或被人大复印资料全文转载。
⑥色散性:消失态的波阻抗(wave impedance)为电抗性,其值强烈地与频率相关,亦代表其色散特性。
⑦超光速性:场的消失性常造成超光速波传播;在理想情况下,消失波(场)没有交变振荡的行波成分,没有相移,时延近于零;这就是在用截止波导的研究中常常发现相速、群速为超光速的原因。1991年笔者在《截止波导理论导论》[3]一书中率先指出在截止波导中消失场条件下不仅相速、群速可能超光速(vp>c,vg>c),甚至可能出现负相速和负群速(vp<0,vg<0);这些理论判断多数已被实验证
明[6-8]。
除此之外,还有其他性质显示这种独特的电磁状态。为了比较,这里再列出对应的天线近场的物理特征:
①按照r-3或r-2的规律,场幅沿r方向迅速下降。

⑤E/H不是常数,故在场强测量技术中必须分别测出E、H。比值E/H具有阻抗的量纲,它与频率有关。
⑥自20世纪90年代以来,不断有实验报告和理论分析指出:在天线近区电磁波可能以超光速传播[9-15]。
在过去的天线理论中,对近区场总是语焉不详。这是因为天线的实用价值总是在远区辐射场体现,因而很少有人对距离天线很近处的情况感兴趣。这与波导的历史相似——开始时人们只关注在截频以上(f>fc)的波导应用(作微波传输线),后来才发现原来在截止区(f<fc)大有文章,不仅应用广泛而且蕴含消失态理论的精髓。例如一般天线书说[5]:“在近区电场与磁场相位相差90°”,了解消失场的人却知道这是不精确的说法。在截止波导理论中[3],只有在完全无耗的理想情况下电场与磁场相位差才是90°,而在有损耗(实际上均有耗)情况,这个相位差比90°略小;故平均Poynting矢不为零,有微量功率传输。又如一般天线书说[5],对于感应场“电磁能量在场源和场之间来回振荡,在一个周期内场源供给场的能量等于从场返回场源的能量,故无能量向外辐射”;然而截止波导理论告诉我们,虽然纯粹的消失场不携带有功功率,但却通过交互作用产生一个不大的有功功率流,对此早就有解析式的证明[3]。参考Feynman的吸收体理论[5],我们就可以对推迟解和超前解的联合与可能的相互作用有更深刻的理解,并将这些概念引入到天线近区场的分析和研究中。
5 早期的自由空间超光速现象研究
1991年的Giakos-Ishii实验[9]似为微波异常传播的最早实验;我们简称其为GI实验,它曾引起科学界的争论。图4是实验时天线的位置,(a)表示接收天线既可面对发射天线(d=0)又可平移到一侧(d≠0);(b)表示接收天线可以在平移之后旋转一个角度,但仍朝向发射天线口面。实验设备及安排如下:用X波段的速调管产生微波载波,并由HP715A脉冲发生器作外调制,该发生器由时域反射计HP1415A的输出口触发器触发,供给HP715A电源也用于驱动速调管。速调管通过铁氧体隔离器送出信号,该信号是受调制的微波脉冲,上升时间为22ns,持续时间为50ns,重复频率147kHz,通过喇叭(口面9.5cm×7.1cm)发射出去。接收喇叭口面距发射喇叭口面距离为l。当二者的口面相对时,从发射脉冲与接收脉冲之间的时间延迟(时延τ)可算出自由空间的本征速度,约为3×108m/s。

图4 美国小组实验时的天线布置
GI实验所用微波频率f=8.245GHz,相应波长λ =3.64cm;如喇叭口面直径 D=9.5cm;则 2D2/λ≈50cm;实际上两喇叭间距为42.7cm及71.5cm,在。图5是实验结果,小圆圈是按图4(a)布置取得,小三角是按图4(b)布置取得。可见,超光速现象在l小时(42.7cm)更突出,证明异常传播不是发生在远区(far-field region)。另外,图4(b)的布置,超光速现象比图4(a)明显;至于为何如此,则尚不清楚。

图5 GI实验结果
再看1993年、1996年意大利电磁波研究院的研究。1993年文章[10],实验所用的微波源是速调管(f=9.5GHz,λ =3.16cm),由 PIN 调制器按阶跃信号调制,下降时间小于10ns,适于测量小于1ns的时延。测量仪器采用Tek2440示波器,测时延精度达到0.1ns。文献[10]的中心内容可概括如下:用发送、接收喇叭测量了微波在空气中近距(小于1m)传播时的脉冲延迟。它们相对时,观察到对应于光速c的时延。如果接收喇叭相对于发送喇叭移动或倾斜,时延减少,表现出超光速。微波异常传播是通过波速v>c而表现出来的,而波速的测量是间接的(实际上是作脉冲时延测量)。而上述异常现象,在喇叭间距加大时即自动消失,即异常现象是出现在发射天线的

图6 意大利小组实验时的天线布置
图6是实验室采用的天线布置,左为发射天线,右为接收天线。天线间口面间距为l,最大距离为L;d表示天线轴线间的距离(d=0表示口面相对,d≠0表示接收天线平移开适当距离)。表2是实验时的参数。故发射天线口面有两种情况,即9cm×8cm(最大直径 D=9cm)和 13.5cm ×10.5cm(最大直径 D=13.5cm)。前者2D2/λ≈51cm,对(a)而言属,对(b)、(d)而言属后者 2D2/λ≈115cm,对(c)、(e)属近.区.,但(e)的 L >2D2/λ,故(e)在近远区之间,从实验结果看,近区、远区都有异常传播的情况。

表2 意大利小组的实验条件和/计算值
综合实验情况,当发射天线不动而接收天线从口面互相对准位置向一侧平移时,间距小时测得时延明显减小,间距中等时仍有此现象,间距大时现象消失(两种发射天线均此规律)。故只在近区有超光速(FTL)现象。在厘米波波长条件下,这个近区大约在0.5m以内。
1996年文章[11],实验设备、微波频率均与1993年相同。仍然是用脉冲对微波进行调制,通过发射天线(角锥喇叭)发射出去,接收天线(角锥喇叭)收到后用检波器检出包络曲线,测出相时延(phase time delay)后确定波速。文章给出以下实验结果:①天线互相面对,间距 l=0.53m;测出时延 τ=3.2ns,对应的传播速度v=c。②接收天线横向移动d=16cm,测出时延τ=2.4ns,对应的传播速度v=1.25c;修正后,确定在空气中传播速度 v=2c。因此,意大利小组的研究结果在1996年文章中表达得更加明确了。在近区以及在近区、远区分界处,均可能出现异常传播(FTL)现象。
A.Ranfagni等的解释是,这里有消失波的一个特殊类型存在,这种类型的波叫漏波(leaky wave)。根本问题在于,仅在有消失波出现时,人们才能把开放空间(open space)的情况与量子隧道过程作比较。上述特殊的衰减波又称复合波(complex waves),其波阵面(波前)垂直于这样一个平面,大致与发射喇叭的垂直平面重合(见图7)。

图7 复合波的示意
根据意大利小组的实验安排,由于l/λ=53/3.16=16.8,显然属于辐射性近场区。目前的研究已涉及天线理论的艰难部分,即发送天线的近场区的场结构和性质。意大利小组测出的传播情况,应是电抗性近场与远场两种情况之间的物理状态。
现在谈谈笔者的看法。我们认为A.Ranfagni等仍用消失波原理来解释微波异常传播的FTL现象是正确的。当接收喇叭平移距离d,异常现象便呈现出来。这说明消失波在两侧的存在,在那里形成了与截止波导内的电抗性场相似的条件。因此,引用和对照消失态理论就有必要。在截止波导里,突出的特点便是有电抗性消失场,在一定条件下甚至成为准静态场(电容性的电场或电感性的磁场,视模式而定)。
参考前述的“电抗性近场”的情况,我们可以假设在意大利小组实验中出现的是TM极化的消失波型。

图8 在微波实现的超光速实验装置
2000年5月,D.Mugnai等[12]发表了题为“波传播超光速行为的观察”的论文。文章说,用局域化微波(localized microwaves)在波长数十倍的距离上以实验演示了超光速波传播,这类波优于消失模隧穿,因后者常常只在几厘米距离上表现出来(消失模特性决定了距离很短),现在的演示可达1m以上。图8是测量微波传播速度的发送与接收天线系统,D是圆形辐射缝隙的平均直径,实验时取D=7cm以及10cm。信号形式为微波脉冲,载频 f=8.6GHz(波长 λ 约 3.5cm),调制为矩形脉冲(升降时间均在纳秒级)。用Tektronix公司的双路数字示波器TDS680B检测时延,实验方法为,改变发送天线与接收天线的间距(L=0.3m-1.3m),作时延测量。图9为时延τ与距离L的关系,实际测量值用黑色圆点表示,它们联成一条直线,其斜率比光速线略小,由此可知实际的波速比光速略大

即比光速c大了5.3%;这个v值是平均的电磁波速度。

图9 时延与距离关系的测量结果
6 近年来的自由空间超光速现象研究
1999 年 W.D.Walker[13]著文讨论“偶极子在近场区的超光速电磁场”,虽是无实验的理论分析文章,却有独到之处—对天线近场区的研究是分别计算相速和群速。例如对简谐变化的场:

过去的讨论只取k=k(ω),即k仅与频率有关;但在天线近场区的研究中应取k=k(ω,r),即k与径向坐标 r有关。这样一来,对等相面取 ωt-kr=Const.,即,也就是:

由此得

过去一般认为k与r无关,分母第2项为零,故vp=ω/k;显然这不严格。取相角θ=-kr,从而有

故得

然而 k=ω/c,故有

类似地,在波群(wave group)由不同频率的波组成时,可以定义群速:

Walker还导出(根据近场时的Er):

他的结论是:由振荡的电偶极子产生的近场区电磁波和波群,由于靠近源,电磁波以的速度传播;但在r=λ时降为光速。他认为群速(group speed)是已调波信息速度和波的能量密度传播速度。
2009 年 N.V.Budko[14]发表论文“自由空间中电磁场的局域负速度观测”,把相关研究推进到新的高度。文章指出,1983年国际上作出了用真空中光速c确定长度的决定,由于给出了c的精确值,测量光的实在速度的工作终结了。然而存在一个简单问题:究竟是什么精确地以299792458m/s的速度行进?一种说法是“真空中电磁脉冲的波前(wave front)”,通常又假定跟随其后的波形也是该速度。这假定对雷达测距等是必要的。然而,某些实际上有用的波形并非以光速前进。理论与实验表明,矢量电磁场的近场、中场动力学比简单的向外传播要复杂许多。存在一个靠近源的区域,在那里波前以光速向外行进,亦即可能有波形行进(travel back in time)。该文章的图3是negative waveform velocity的实验观测。总之,Budko文章认为发现了而且在(3.5-8)mm的头5个近场波形,显示内峰
2012年樊京等[15]提出论文“电磁感应在自由空间以超光速传播”。摘要说:“报道了设计了测试数据表明,自由空间条件下,电磁感应速度在10倍光速以上。基于磁偶极子的解析解和基于有限元分析的数值解支持我们的结论。本工作可能改变人们对变压器工作原理的认识,同时也为提供了一种可能的新方法。”以上引文中的着重号(圆点)为笔者所加,其实验系统见图10。的传播方向,近场群速度低于光速,相速度高于光速的情况;在电磁感应的方向,相速度和群速度均超光速。②为什么近场会出现特殊光速?本质上,Maxwell方程在静态和动态是不协调的。Poynting能量在推广到静态时会产生悖论。这就引出了19世纪曾经激烈辩论过的一个问题:‘场’和‘源’的作用是否相同?赵凯华认为“位移电流与传导电流不以同样规律激发磁场”,其

图10 磁偶极子(环天线)测量系统
在与冯正和教授讨论时,樊京深入谈及他的想法:“①关于近场的群速和相速问题首先要区分电磁波矢量k的传播方向和电磁感应的传播方向,这两个方向是正交的,不能混淆。根据相速度和群速度的定义,我们可以解析计算出电偶极子和磁偶极子的速度。对此请看W.D.Walker的计算和黄志洵老师对波速问题的讨论。结论是这样的:在电磁波实就是区分开了场和源。在近场,源的作用占优势;在远场,场的作用占优势。但有一个例外,在我的实验中,Z轴方向没有Poynting矢量的传播。Maxwell方程的本质是波动方程,按照我的理解,波动方程总会有横波解和纵波解,横波解的速度往往比纵波快,例如地震波。Maxwell当年假设以太是不可压缩流体,按照动力学的观点,这个纵波速度就应该是无穷大。为什么我们从来没有看到Maxwell方程的纵波解?”因此,樊京等不仅做成功了磁偶极子天线近场超光速实验,还提出了一些值得思考的理论问题。
7 讨论
过去常有人说,SR理论对“超光速不可能性”的判断是针对真空条件(自由空间条件)下的c值,如让光(或其他电磁波)通过某种媒质就与上述条件不符,因而失去意义。然而,近年来,多项理论与实验研究已证明即使在自由空间情况下,超光速也是存在的;这就证明了超光速现象的普遍性。至于如何理解“近场超光速”,理论上还应进行工作。
2012年秋梁昌洪[16]的书《电磁理论前沿探索札记》出版,由于其内容生动、丰富、深刻而引起关注。该书第一篇(“静电场的自作用能”)的论述恰好与笔者近期的思考一致,其中讲到1940年秋Feynman遇到电磁理论上的问题——由于把电子看作点粒子,电子自作用能成为无限大。Feynman于是假定“电子不能对自己产生作用”;又提出“辐射阻尼可看成为由吸收体电荷以的形式对源的一种反作用”。梁昌洪认为,这种理论的最大特色在于“既不出现电磁场,也不存在电荷对自身的作用”。我们觉得这些理论思考对认识电小天线(是电流源而非电荷源)的近区场特性,以及这种特性导致的超光速乃至负速度现象,是有启发的。
本文的中心思想是:存在着一种可称为evanescent-state like(类消失态)或 quasi evanescent-state(准消失态)的电磁场状态,天线近区场就是这种状态。由此而解释实验中发现的“近区场超光速”,就比较容易了。科学家和实验员的工作都重要,但后者只是就事论事地提供事实;虽然这也不容易,但更难的是前者,即必须对实验现象作出数学和物理学的解释。
2010年笔者写作“虚光子初探”一文,它未在杂志上发表而直接收入到2011年出版的书《现代物理学研究新进展》[17]之中。文章说:“负波速现象确实对因果律形成冲击,有的物理学家感到不可理解,但它是由实验反复证明了的客观存在”。又说:“负相速比负群速更为奇怪和不可思议——电磁波行进一段距离后产生滞后相角,而在消失态情况下却可能产生超前相角,代表负相位常数和负相速的物理意义”。现在重读这些话产生了新的想法:首先,负波速概念也受Causality(译为因果性较好)的阻击,一如前述的超前解;这就暗示两者的联系和一致性。其次,电磁波超前解现象并非只在天线条件下存在,在传输线(波导)中也存在——例如截止波导中(消失态)所可能呈现的负相位常数(β<0)和负相速(vp<0)现象[3]。最后,这些情况验证了本文主旨的正确性和意义,即天线近区场的超光速现象(含负速度现象)本质上是一种类消失态物理条件产生的现象,故在近区场研究方法上可以充分借鉴消失态研究[18]。
回顾历史,1907年Einstein发表文章“关于相对性原理及由此得出的结论[19],其中的§5(“速度的加法定理”)内容既与信号速度有关,又与负速度有关。文章说,假定沿参照系S的x轴放一长条物体(图11),相对于它可以用速度u传递某种作用(从长条物体来判断),并且不仅在x轴上的点x=0(点A),而且在点x(点B)上都有对S静止的观察者;在A处的人,通过长条物体传给在B处的人,长条物体以速度v(<c)沿(-x)方向运动。那么,根据SR,信号速度为


图11 Einstein讨论信号速度间所用的图形

式中,l为物体长度。如u>v,则选择v(<c),总能使ts<0。这就出现了负的传递时间,以及负的信号速度。Einstein认为,这种传递机制造成“结果比原因先到达”,因此“不可能有这样的信号传递,其速度大于真空中光速”。他又说:“虽然这种结局单从逻辑上考虑可以接受,并不包含矛盾;但它同我们全部经验的特性是那么格格不入,所以u>c假设的不可能性看来是足够充分地证实了的”。
我们在此重提Einstein的1907年论文,不是为了评论他的判断(信号速度不能超光速)的对错,更不在此讨论相对论。而是指出我们注意到:①他的分析里同时出现了超光速、负时间、负速度;②他使用Causality帮助自己作判断;③他认为违反因果性的事可以不违反逻辑,只是由于它违反人类经验,所以才说“信号速度不可能超光速”;④他不做百分之百的肯定;那种不确定的语气,仿佛为今天的超光速研究留下了空间。
2000年WKD实验[7]公布,而这是一个典型的负群速(NGV)实验。两年后,刘辽[20]评论说,该实验是“直接显示了超前场存在”。作为一位资深的相对论学者,他还认为这类实验对旧有理论形成了冲击,甚至是在实验室中实现了所谓时间机器(time machine)的效应。可以看出这位专家的态度是积极而开放的,不像有的理论物理学家断然否认超光速和负群速有实现的可能[21]。刘辽教授还认为,Causality的精髓并非像一般人所理解的那样,主要体现在时序上——“原因”(cause)先于“结果”(effect);最重要的是(文献[20]的原话是“果不可能通过任何方式影响因”)。这就维护了自然规律的客观性(人不能改变历史),又可以解释一些新出现的物理实验。笔者认为这位老专家的观点是正确而又深刻的,他的科学态度值得学习。
本文把天线近区场超光速现象、消失态电磁现象、超前波、负波速联系起来理解讨论,并在此纠正自己过去的一个说法(“负相速比负群速更为奇怪和不可思议”)。其实负相速并不奇怪,它就是超前波。另外,笔者在研究工作中注意到如下的情况:超光速波速(例如vg>c)与负波速(vg<0)这两者常常在同一实验系统中相伴相生——这虽能用Brillouin图解释,但还是引人注目。总之,虽然自然界复杂、奇妙,但它总归是可以认识的。
[1]黄志洵.对开放空间中微波异常传播现象的探讨[J].北京广播学院学报(自然科学版),2000,(3):10-18.
[2]黄志洵.超光速研究新进展[M].北京:国防工业出版社,2002.
[3]黄志洵.截止波导理论导论(第2版)[M].北京:中国计量出版社,1991.
[4]Gleick J.Gennius:the life and science of Richard Feynman[M].New York:Newton Publ Co.1992.
[5]杨思耀,杜加聪.天线[M].北京:电子工业出版社,1987.
[6]Wynne K.Tunneling of single cycle terahertz pulse through waveguides[J].Optics communication,2000,176:429-435.
[7]Wang L J,Kuzmich A,Dogariu A.gain-asisted superluminal light propagation[J].Nature,2000,406:277-279.
[8]黄志洵.论电磁波传播中的负速度[J].中国传媒大学学报(自然科学版)[J].2007,14(1):1-11.
[9]Giakos G C,Ishii T K.Anomalous Microwave propagation in open space[J].Microwave and Opt Tech Lett,1991,4(2):79-81.
[10]Ranfagni A.Anomalous pluse delay in microwave propagation:A plausible connection to the tunneling time[J].Phys Rev E,1993,48(2):1453-1460.
[11]Ranfagni A,Mugnai D.Anomalous pluse delay in microwave propagation:A case of superluminal behavior[J].Phys Rev E,1996,54(5):5692-5695.
[12]Mugnai D.Observation of superluminal behavors in wave propagation[J].Phys Rev Lett,2000,84(21):4830-4833.
[13]Walker W D.Superluminal near-field dipole electromagnetic fields[J].http://www.arXiv.Org,1999.
[14]Budko N V.Observation of locally negative velocity of the electromagnetic field in free space[J].Phys Rev Lett,2009,102:020401 1-4.
[15]樊京,周冶平.电磁感应在自由空间中以超光速传播[J].即将发表的论文,2012.
[16]梁昌洪.电磁理论前沿探索札记[M].北京:电子工业出版社,2012.
[17]黄志洵.虚光子初探.见:现代物理学研究新进展[M].北京:国防工业出版社,2011.
[18]黄志洵.论消失态[J].中国传媒大学学报(自然科学版),2008,15(3):1-9.
[19]Einstein A.The relativity principle and it’s conclusion[J].Jahr.Der Radioaktivität und Elektronik,1907,4:411-462 中译:关于相对性原理和由此得出的结论[A].范岱年,赵中立,许良英译.爱因斯坦文集·第2卷[C].北京:商务印书馆,1983,150-209.
[20]刘辽.试论王力军实验的意义[J].现代物理知识,2002,14(1):27-29.
[21]张元仲.反常色散介质‘超光速’现象研究的新进展[J].物理,2001,30(8):456-460.
