基于谱图的联合时频域主用户信号检测技术

杜利平 李 飞 周贤伟

（北京科技大学计算机与通信工程学院，北京100083）

引 言

随着无线通信技术的迅猛发展，频谱资源紧缺和频谱需求扩大之间的矛盾日益凸显.世界各国现行的频率使用政策除分配极少的工业、科学和医用频段之外［1］，大多采用许可证制度.而获得许可的用户，并非全部都是全天候占用许可频段，一些频带部分时间内并没有用户使用，另有一些偶尔才被占用，即使系统频谱使用率低，仍无法将空间的频谱分配给其他系统使用，即无法实现频谱共享.认知无线电作为解决这一矛盾的主要技术得到了越来越广泛的关注.在认知无线电系统中，认知用户需要对周围的频谱环境进行准确和快速的感知，因此，主用户检测技术在认知无线电网络中非常重要［2］.常用的频谱感知方法主要有：能量检测法、匹配滤波器法、循环谱检测法［3］和合作频谱感知法［4-5］.能量法由于算法简单易行最为常用.但是能量检测需要预知噪声方差，而在实际情况中噪声方差往往是未知的［6-7］.同时，噪声方差的不确定性对能量检测的影响很大.匹配滤波器法能获得较好的感知性能，但是需要主用户信号的先验知识，并且系统实现复杂.循环谱检测法利用信号的谱相关特征进行检测，低信噪比情况下有较好的检测性能，但计算复杂度较大，检测时间长.

随着频谱感知研究的深入和对实现应用的需求，人们发现不同维度的频谱感知以及多维度之间的联合频谱感知对于频谱的分析、决策和动态分配都是非常重要.不完整的频谱资源空间特征不利于更高性能的无线频谱资源分析和分配.近两年来，多维频谱感知研究逐渐成为国内外学者关注的问题.文献［8］对频谱机会的定义中也说明主用户信号应该至少具有频谱空间中时间维、频率维和空间位置维等三维信息.多维频谱感知的研究目前相对较少［9］.而利用距离-多普勒谱图来进行多维频谱感知研究目前还没有发现.

在设计主用户检测算法时，人们考虑的主要因素有两个：一个是在低信噪比条件下仍具有高的检测性能；另一个是感知时间延迟尽量小.参数谱估计根据对过程的先验知识，建立一个近似实际过程的模型，而后利用观测数据或相关函数来估计假设的模型参数，进行识别或谱估计，避免了数据观测区以外的数据假设问题，从而避免功率泄漏，即使是在低信噪比条件下仍具有很高的频谱分辨率［10-11］.针对上述两大因素，我们提出了基于自回归（AR，Auto-regressive）模型的检测统计量，通过谱密度峰值来分析并判断主用户信号的存在，并结合距离-多普勒谱图实现对主用户的时间和频率维的感知方法.本方法不仅提供了多维的感知信息，同时保证了低信噪比下的高检测性能.另外，AR模型预测的数据延拓功能使得AR模型特别适用于处理短数据，从而保证感知延迟很小.MATLAB仿真结果给出了时间和频率维的检测结果，并表明了本方法比能量法（ED，Energy Detection）具有更好的检测特性.

1 基于AR模型的主用户检测算法

1.1 信号模型

假设发射机检测信号的基本模型为

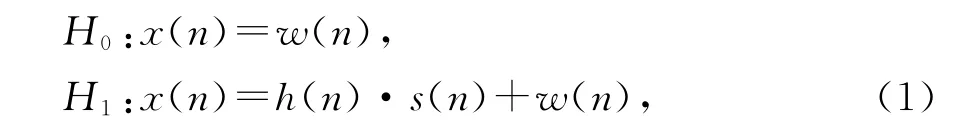
式中：x（n）是接收到的信号；s（n）是主用户发送信号；w（n）是加性白高斯噪声；h（n）是信道的增益；H0表示信道未被占用，表明了目前在这一确定频段上没有主用户；H1表示信道被占用，表明目前存在主用户.本文假设信号是加高斯白噪声信道的情况，信道增益h是确定的.

接收信号可用AR模型表示为

式中ωn为输入方差为σ2的白噪声，α1，α2，…，αp为待估系数.则接收信号AR模型功率谱密度可表示为［12］

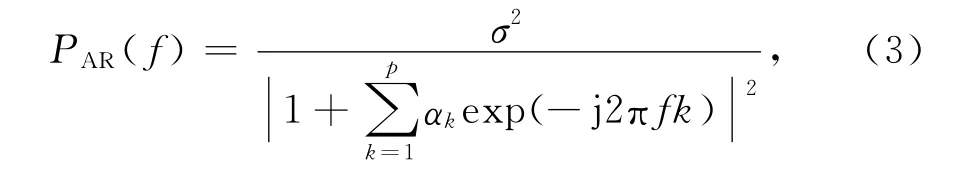
其中PAR（f）是对应的功率谱密度.由上可见AR模型法估计功率谱实质是求解模型系数α1，α2，…，αp和σ2的问题.常用的求参数的算法有：Yule-Walker算法，Burg算法，协方差算法，改进协方差算法和Levinson递推算法等.本文采用Levinson递推算法.

AR模型输出可以看作是将方差为σ2的白噪声激励一个线性移不变系统的输出，其中线性移不变系统的频率响应是

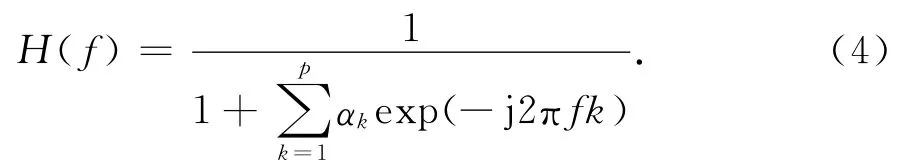
假设输入信号的功率谱密度为Pxx（f），则线性系统输出信号的功率谱密度为

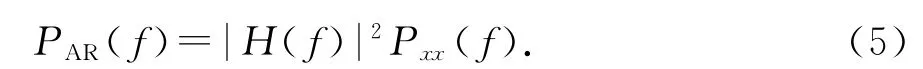
由于宽带随机过程（非高斯）通过窄带线型系统，系统输出可以得到接近于高斯分布的随机过程.因此，AR模型输出是近似高斯分布的随机过程，其功率谱密度PAR（f）符合χ2分布.其均值

式中，μx为白噪声激励信号的均值.当μx＝0时，μAB＝0.假设PAR（f）的方差为σ2AR.

1.2 AR模型阶数选择

AR模型的阶数p一般不是先验已知的，所以我们需要根据信号的特点来选择一个最佳的阶数.过低的阶数将导致高度平滑的谱估计，而过高的阶数导致谱中出现虚假峰值.人们提出了基于修正预测误差方差的关于阶数选择的标准，包括［13］：final prediction error （FPE），Aikaike’s information criterion （AIC），corrected Aikaike’s information criterion （AICc），Minimum Description Length（MDL），与之相同的Bayesian information criterion（BIC），Hannan-Quinn criterion（HQC）.这几个标准的定义如下：

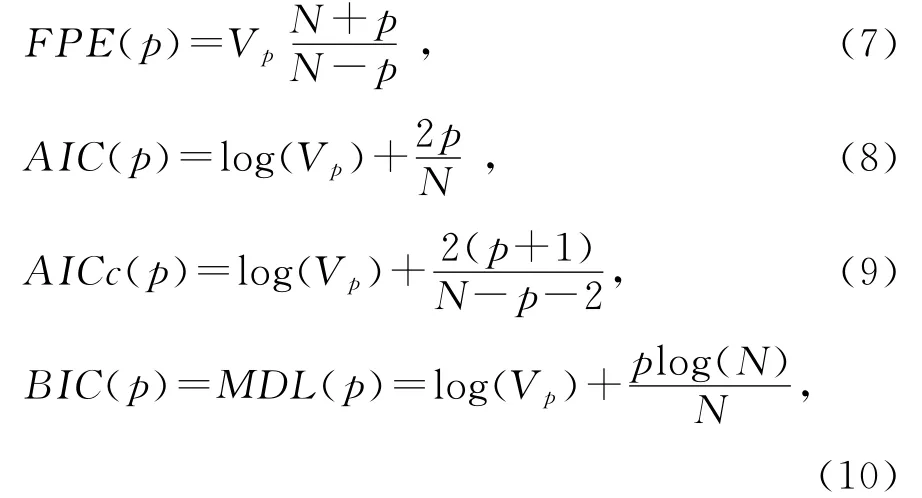
式中：Vp是p阶模型阶数的失真函数（预计误差平方和的归一化），N是序列长度.当标准函数达到最低点时，对应的p值被认为最佳阶数.但是这些方法在实际数据应用时却没有一个能表现得很完美，所以通常需要实际验证［14］.

2 频率-时间维检测

为了缩短感知时间，我们把接收数据分为不重叠的块，每次处理一个数据块.为了简化分析，这里我们假定信号包含在一个块内，则检测模型可以定义为

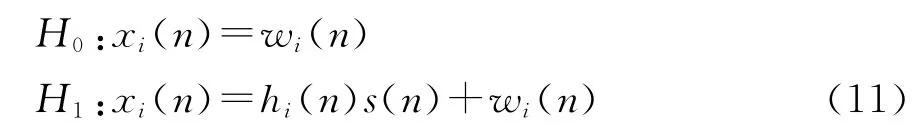
式中：i＝0，1，…，I-1为块序号；n＝0，1，…，N-1为数据块内的采样点序号.xi（n）表示第i个数据块的第n个采样点；wi（n）为加性高斯白噪声；hi（n）为信道增益.则广义似然比检测可以写为

式中：γ为检测量的阈值；PARi为第i个数据块AR谱估计幅度；f为频率.在雷达信号分析中，i又指第i个距离单元，而f是与多普勒频移有关，因此PARi（f）谱图又称为距离-多普勒谱图.

在上节中，我们分析得出，AR模型输出是近似高斯分布的随机过程，其功率谱密度PAR（f）符合χ2分布，即对所有的i和f，都有

由于AR系统输出相互独立，所以虚警概率如下［15］

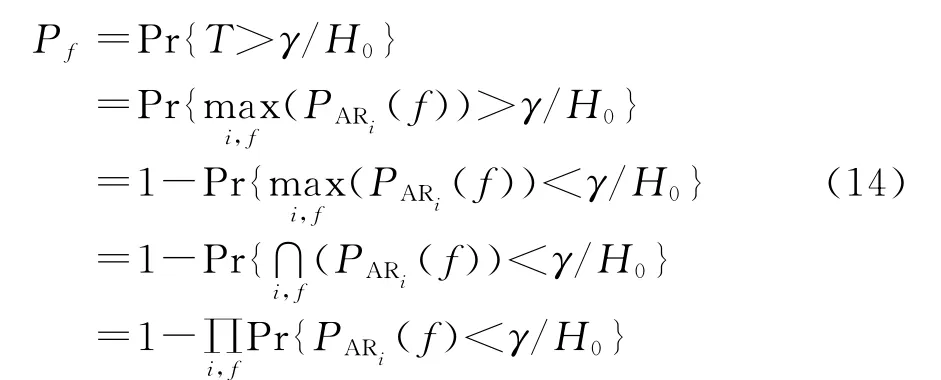
式中，

3 仿真分析

3.1 AR模型阶数选择

在AR模型中，阶数的选择会影响算法的结果，所以必须预先根据信号选择好阶数.在众多阶数选择的标准中，我们选择贝叶斯信息标准（BIC）对阶数进行选择，函数仿真结果如图1所示.

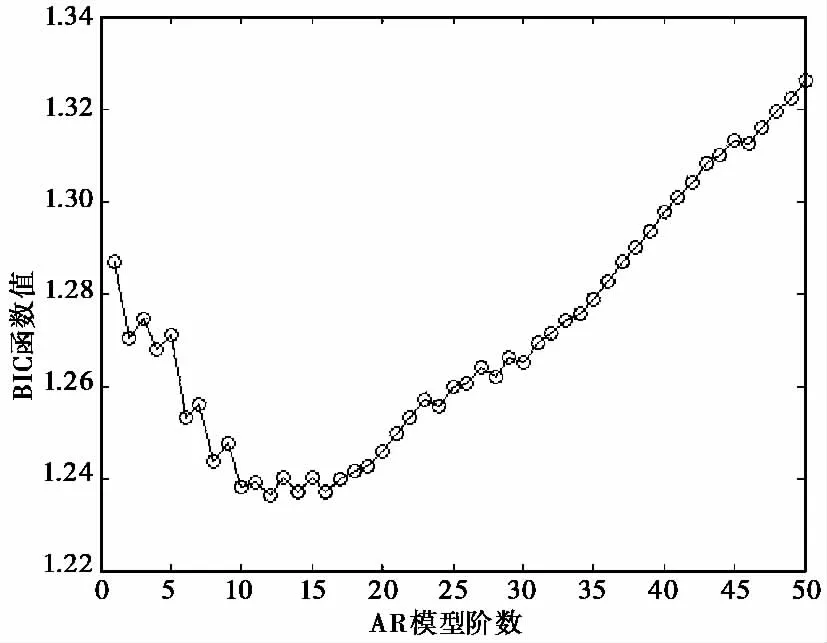
图1 BIC标准函数图

由于阶数选择与输入信号有关，不同随机信号下的阶数选择函数值并不完全相同，但是最低点基本相同，所以为了更适合随机信号，我们可以统计1 000次的BIC函数图的最低点，然后取其平均值，即可得到普遍适用的一个阶数值.根据图1，选取仿真信号的AR模型阶数为15.

3.2 距离-多普勒谱图

假设主用户信号为一随机信号，信号长度为500，以FSK方式进行调制，信道为高斯信道.上述主用户信号在2 000s时出现，信号持续时间为2 000 s.图2为本方法求得的输入信号的距离-多普勒谱图.从图中能看到，在时间为［2 000，4 000］的时候出现了主用户信号，且主用户信号的频率为4Hz.

3.3 接收者操作特征 ROC，Receiver Operating Characteristic）曲线分析

普通信号检测采用的能量法的效果在低信噪比情况下衰减的很强，而AR模型法相对与能量法相比有很大优势，在低信噪比情况下仍然可以得到很好的检测性能.设定SNR＝-12dB，并设定相关阈值，在FSK调制下不同阶数的ROC曲线，并与能量法进行对比，如图3所示.其中ED曲线表示能量法的结果，order2曲线为AR模型阶数为10的结果，order4曲线为AR模型阶数为15的结果.

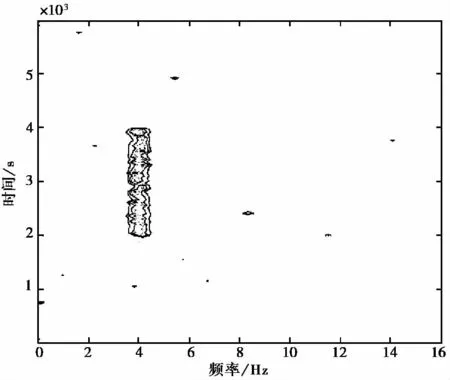
图2 距离-多普勒谱图

从图3中可以明显看出在合适的阶数条件下，AR模型法优于传统的能量法的，检测准确率高.而且当阶数为最佳阶数15时的检测性能要明显好于非最佳阶数10的结果.同时，我们还对其他阶数的结果进行了仿真分析，发现阶数的选择会对感知结果造成影响，随着所选阶数偏离最佳阶数，感知性能会逐渐下降.

3.4 复杂度分析

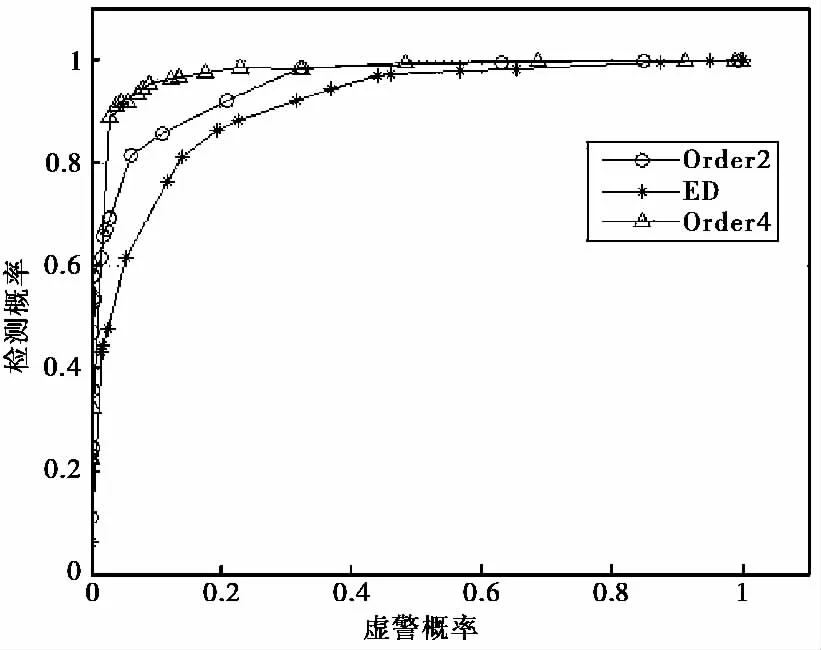
图3 ROC曲线对比图

对于AR模型算法来说，运算复杂度主要在对参数和方差的估计上.由于本文采用Levinson递推求取AR模型系数，从而避免了自相关矩阵估计，算法复杂度较低，为O（N2），而能量法如果采用快速Fourier变换求解，算法复杂度为Nlog2N，其中N为采样点个数.通过二者的比较，我们看出基于AR模型的谱估计方法算法复杂度略高，但检测性能要比能量法好.

4 结 论

利用AR模型得到信号的距离-多普勒谱图，实现了时间和频率上的二维主用户信号检测，并推导得到了虚警概率和门限值的关系式.从MATLAB仿真中可以看出，AR模型应用在主用户检测方面具有比能量算法更好的检测性能，而且随着信噪比的增大，检测性能随之提高.为主用户信号检测提供了一种新的方法.

［1］YEO H Y，JOON H C.An orthogonal cognitive radio for a satellite communication link［C］//IEEE 20th International Symposium on Personal，Indoor and Mobile Radio Communications.Toyko，September.13-16，2009，4，3154-3158.

［2］HAYKIN S，THOMSON D J，REED J H.Spectrum sensing for cognitive radio［J］.Proceedings of the IEEE，2009，97（5）：849-877.

［3］BHARGAVI D，MURTHY C R.Performance comparison of energy，matched-filter and cyclostationaritybased spectrum sensing［C］//2010IEEE Workshop on Signal Processing Advances in Wireless Communications，Marrakech，June 20-23，2010：1-5.

［4］CHAVALI V G，DA S，CLAUDIO R C M.Collaborative spectrum sensing based on a new SNR estimation and energy combining method［J］.IEEE Transactions on Vehicular Technology，2011，60（8）：4024-4029.

［5］赵东峰，周贤伟，程曾伟，等.采用最小最大准则的协作频谱感知融合［J］.电波科学学报，2011，26（5）：923-926.ZHAO Dongfeng，ZHOU Xianwei，CHENG Zengwei，et al.Combination based on the MiniMax rule for cooperative spectrum sensing［J］.Chinese Journal of Radio Science，2011，26（5）：923-926.（in Chinese）

［6］URKOWITZ H.Energy detection of unknown deterministic signals［J］.Proc IEEE，1967，55（4）：523 –531.

［7］SHEN Lei，WANG Haiquan，ZHANG Wei，et al.Blind spectrum sensing for cognitive radio channels with noise uncertainty［J］.IEEE Transactions on Wireless Communications，2011，10（6）：1721-1724.

［8］YUCEK T，ARSLAN H.A survey of spectrum sensing algorithms for cognitive radio applications［J］.IEEE Commun Surveys ＆ Tutorials，2009，11（1）：116-30.

［9］TUAN D，MARK B L.Joint spatial-temporal spectrum sensing for cognitive radio networks［J］.IEEE Transactions on Vehicular Technology，2010，59（7）：3480-3490.

［10］MARPLE S L.Digital Spectral Analysis with Application［M］.NewJersey：Prentice-Hall，1987.

［11］SUN Lisha，WANG Shuwang，SHEN Minfen，et al.A method for parameter estimation of time-dependent AR model using higher-order spectra and wavelet basis［C］//7th International Conference on Signal Processing，Beijing，August，31-September 4，2004，1：288-291.

［12］GENSHIRO K.Introduction to Time Series Modeling［M］.London：Chapman and Hall/CRC，2010.

［13］KHORSHIDI S，KARIMI M，TOWHIDI，et al.Optimal autoregressive（AR）model order selection in the sense of predictive error［C］//18th Iranian Conference on Electrical Engineering，Sfahan，May 11-13，2010：140-144.

［14］ZHOU Hongxia，DU Liping，YAN Hong.Detection of tandem repeats in DNA sequences based on parametric spectral estimation［J］.IEEE Transactions on Information Technology in Biomedicine，2009，13（5）：747-755.

［15］KAY S M.Fundamentals of Statistical Signal Processing［M］.New Jersey：Prentice-Hall，1998.