中国期货市场非交易时段的VaR与ES测度研究

张 舒，仲伟俊，梅姝娥

（东南大学 经济管理学院，江苏 南京210096）

一、引 言

近年来，随着金融市场一体化程度的不断加深、期货交易时间的延长、在开盘之前和收盘之后的信息发布等大量事件的发生，某种程度上已改变了非交易期间可得的财经信息数量及其重要性。目前，我国的商品期货均在白天交易，总交易时间尚不到非交易时段的一半。然而，很多价格敏感的国内外金融信息其实是在相对冗长的非交易期间发布的，如依据前一天收盘后发布的当地或全球性政策公告等。这些信息都可能反映在开盘和收盘时的价格之中，从而加大期货市场风险。并且，非交易时间的长度不同，也使得平均积累的信息总量有所差异。根据时间的长短，我们将非交易时段划分为交易当晚、短期假日、周末假日和中长假日四种［1，2］。并且，Taylor、Tsiakas［1，2］认为，在期货交易及其风险管理中，非交易的金融信息扮演着非常重要的角色，不仅能够为期货市场的价格发现提供预测，还可为风险管理中的风险测度提供必要的信息支持。因此，我们只有对非交易时段的市场风险进行清晰的认识与测度，才能利用有价值的金融信息对期货市场进行有效利用和管理。

二、文献综述

风险价值（Value at Risk，VaR）方法被用来度量和管理损失，其最早来自Baumol［3］在管理科学领域的应用。在20世纪90年代，J P Morgan建立了用来度量资产市场损失的一种经典的风险价值法，其经济学意义是指在给定置信度水平下，某一金融资产或证券组合在未来特定的一段时间内所遭受的最大可能损失。VaR现已发展成为现代风险管理的国际标准和理论基础。VaR之所以迅速在各国金融机构广泛应用，很大程度上是因为它是描述给定组合可能遭受损失大小的一种方法，且具有灵活性，能够满足各种金融机构的需要。但是VaR本身也存在一些局限，对VaR方法的批评主要在于其不满足一致性，尤其是次可加性［4］。另外，VaR只能度量正常情况下的最大损失，对于因为风险因子波动产生的极端情况，并不能有效度量。VaR方法的不足之一来源于概念或是理论上的局限性，不足之二是它需要对金融市场的趋势做理论上的假定，如分布的正态性等问题。为弥补这些不足，Engle和 Manganel［5］于1999年提出了预期损失（Expected Shortfall，ES）的概念。ES值是损失超过VaR的条件均值，反映了超额损失的平均水平。一些学者［6-8］已经证明，计算厚尾数据（非正态分布）时，使用ES模型来测度风险，会得到更好的估计效果。且ES方法可以用作度量超过VaR的损失，满足并符合由Artzner在1997年提出的一致性公理［9］。由此，结合 VaR和ES的双风险门限的监管将对企业和金融机构提供更加合理、有效的风险度量标准，目前这一方法正日益受到各方重视。

在VaR的计算中，最关键的是对资产价格变化的累计分布函数进行假设，计算分布函数的现有方法主要有：风险矩（Riskmetrics）法、GARCH法、分位数法和极值理论（Extreme Value Theory，EVT）［10］。风险矩法是假设资产组合的日连续复利收益服从条件正态分布；GARCH法主要是利用条件异方差模型进行分析，针对模型中误差项分布的不同假设又分为基于高斯分布、学生t分布和广义误差分布的GARCH模型等；分位数法是估计VaR的一种非参数法，它不需要对资产的收益进行假设，目前主要分为两类：经验法和分位数回归法；极值理论主要对极端市场情况下的风险损失进行估计，可以准确地描述分布尾部的分位数。使用极值理论来建立VaR管理机制的背景主要在于一般权益市场（或其它金融机构）大都使用简化的VaR风险管理制度（俗称的σ-based的VaR），这些简化的VaR制度是在正态分布的假设下运行的，当风险事件发生时，概率分布将偏离正态性，从而出现厚尾极值现象［11］。此时，简化的VaR将出现严重偏误，而基于极值理论的VaR则可有效避免这些偏误。由于绝大多数金融时间序列是非对称的，在计算VaR的各种方法中，极值理论方法将比传统方法更适合于对厚尾极端分位点的预测。

近年来，国内学者在期货市场风险价值中的应用方面进行了一系列研究，取得了不少有价值的成果。迟国泰等［12］借助多元 GARCH（1，1）模型所预测的多种期货组合的协方差矩阵，计算了该期货组合的波动值，并结合风险价值建立了基于多元GARCH-VaR的多种期货合约组合市场风险评价模型。韩德宗［13］以郑州商品交易所的硬麦期货和上海期货交易所的铜期货为例，计算了收益的VaR值，对预测结果的有效性进行了检验。刘庆富等［14］利用基于广义误差分布的 VaR-GARCH（1，1）模型对我国期货市场风险进行了测度。虽然如此，当前对期货市场的风险测度主要集中于传统收益的风险测度上，而对我国期货市场非交易风险的测度尚未涉及。为此，本文将试图利用基于极值理论的VaR和ES模型对这一问题进行探索。

三、非交易收益与风险测度模型

为计算期货市场的非交易风险，下文首先给出非交易收益的测度公式，在此基础上，分别给出基于极值理论的风险测度模型。

（一）非交易收益的测度公式

根据前文非交易时段假日的分类，借鉴Tsiakas［2］界定股票市场非交易收益的思想，下文具体给出期货市场非交易收益的数据生成过程。用Pct表示t日收盘价格，表示t日开盘价格。那么，每日收益rt、日间交易收益和非交易收益可分别表示为：

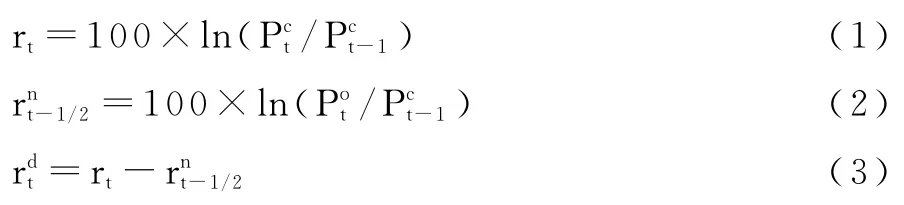
定义每日收益时，时间为整数，而非交易收益定义为整数时间的一半。根据这一标准，我们把非交易期间按照时间长度划分为四类互不重叠的非交易收益：（1）为周一至周四交易当晚的收益，测度的是前一日收盘到当日开盘这一时段的收益；（2）为短期假日的收益，测度的是当日下午收盘到隔日开盘这一时段的收益；（3）为周末假日的收益，测度的是周五收盘至周一开盘这一时段的收益；（4）为中长假日的收益，测度的是假日在周一或周五时，假日前收盘到假日后开盘这一时段的收益。短期假日、周末假日和中长假日分别比交易当晚至少长24小时、48小时和72小时［23］。

（二）基于EVT的风险测度模型

1.VaR与ES模型的建立

极值理论是度量市场风险极端情形的一种方法，它具有超越样本数据的估计能力，并可以准确地描述分布尾部的分位数，利用它来计算的VaR和ES可以实现更高的精确度。极值理论主要包括两类模型，即传统的分块样本极值模型和近年来发展起来的POT（Peaks Over Threshold）模型。分块样本极值模型是对大量同分布样本分块后的极值进行建模，所以需要采用大量的数据，实际中往往不能满足这一条件。POT模型则是对样本数据中超过某一充分大阈值的所有样本数据进行建模，即只是考虑对尾部的近似表达，而不需要对整个分布进行建模，这就克服了其他度量方法在解决厚尾分布上的缺陷，可以对损失分布直接进行数理分析。并且POT模型使VaR和ES值的计算更为简便。其中，广义帕累托分布（General Pareto Distribution，GPD）是广泛应用的一种POT模型。

设随机变量X服从分布函数F，VaR被定义为在给定置信水平q下未来一定时间内期货收益所遭受的最大可能损失，即 VaRq＝F-1（1-q）（F-1为分位数函数）［9，15，16］。若置信水平q给定，我们可得到VaR的测度公式：

以VaR为基础，可以计算超过VaRa的预期损失 ES［15］，其计算公式为：

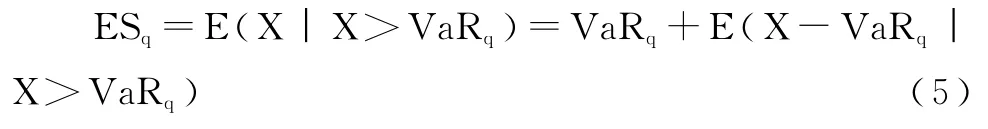
其中，E（X-VaRq︱X＞VaRq）为给定阈值 VaRq时的均值超越函数（Mean Excess Function）。当ξ＜1时，我们有：

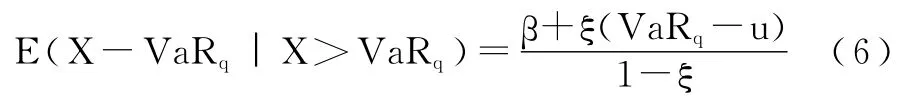
由等式（5）和（6）可以求出ES的表达式：

其中，u为时间序列的阈值，ξ为分布的形状参数，β为与阈值u有关的尺度参数。

2.超越阈值分布的选择

POT方法关注超过某一阈值的分布状况。为此，我们设每日收益变化的随机变量Xi（i＝1，…，n）是独立同分布的，它们的共同分布为F（x）＝Pr（Xi≤x）。选取一个阈值u，使得u小于F支撑集的右端点，即u＜ω（F）＝sup｛x∶F（x）＜1｝。我们记X为任意的Xi（i＝1，…，n）并定义超越阈值u的超额数y的条件概率分布为：

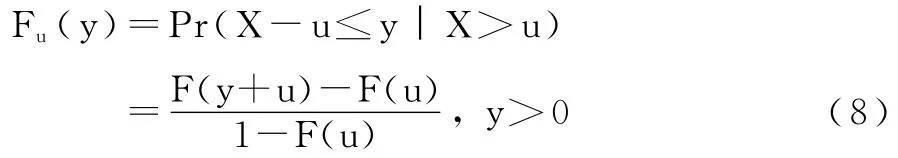
称Fu（y）为超阈值分布。Balkema，Haan和Pickands［17，18］已证明，对充分大的阈值 u，超阈值分布近似为广义帕累托分布：

其中，β（u）为与u有关的正函数，表示尺度参数；ξ（∈R）为分布的形状参数；尺度参数β（u）和形状参数ξ决定着广义帕累托分布的具体形状。当ξ≥0时，y≥0；当ξ＜0时，0≤y≤-β（u）／ξ。当ξ＞0时，F来自Fréchet分布簇，Gξ，β（u）为重新参数化的普通Pareto分布，它具有厚尾特征；当ξ＝0时，F来自Gumbell分布簇，Gξ，β（u）为指数分布，它与指数分布相对应，具有正常的尾部；当ξ＜0时，F来自Weibull分布簇，Gξ，β（u）为paretoⅡ型分布，它具有薄尾特征。而ξ＞-0.5时，μ、β、ξ的最大似然估计符合一致的和渐近的正则分布，渐近的方差可以通过观测信息矩阵的反函数求得；当ξ＜-1时，最大似然估计一般不可能得到。在实际的极值建模中，当ξ＞-0.5时，将很难遇到。当ξ＞0时，广义帕累托分布是厚尾的，这与本文的风险测度是最为相关的。

3.VaR与ES模型的估计

（1）阈值的选择

在正确估计参数β和ξ之前，需要选择合适的阈值。若阈值过高，将导致较少的超越量，估计方差较大；若阈值太小，将无法满足超越量近似服从广义帕累托分布的条件，会使得估计量成为有偏估计。因此，我们须权衡有偏和方差之间的关系，选择适当的阈值。下面介绍几种较常用的确定阈值的方法。

①基于GPD的均值超额函数。均值超越函数e（u）可表示为：

其中，Xi（i＝1，…，n）表示超过阈值的样本观测值，n为超越量个数。对某个阈值u0，如果超越量分布近似服从参数为β（u0）、ξ的广义帕累托分布，则对大于u0的u、e（u）应该为线性近似的。由此，定义点集｛（u，e（u））∶u＜max（Xi）｝，由这些点集构成的图形称为平均剩余寿命图（Mean Residual Life Plot）。选择适当的u0（＞0）作为阈值，可使得u≥u0的e（u）近似为线性。

② 观察参数的稳定性。在阈值取值范围内，利用超越量估计出GPD的参数β和ξ，若初始阈值u0对应的超出量近似为广义帕累托分布，则对大于u0的阈值形状参数ξ的估计值应该保持不变，且尺度参数有如下关系：

令β′＝β（u）-ξu，若β′与u无关，则称式（11）为修正的尺度参数（Modified Scale）。由此，作β′和ξ关于u的图形及与之相对应的置信区间，并可选择使这两个估计量能保持为常数的最小值的u作为阈值。

③ Hill图示法。令X（1）＞X（2）＞…＞X（n）表示独立同分布的有序数列，尾部指数Hill的统计量可定义为：

在实际应用中，我们常综合运用两种或两种以上的方法，以更准确地确定阈值［23，24］。

（2）模型的估计

对参数β（u）和ξ的估计，我们将利用极大似然法得到。假设X1，X2，…，Xn为来自同一未知分布F的样本观测值，对于一给定的阈值u，称满足条件Xi-u＞0的样本Xi为极值，分别用X（1），X（2），…，X（k）表示，并定义超阈值量yi＝X（i）-u（i＝1，2，…，k）。当阈值u足够大时，我们可以认为超阈值量y1，y2，…yk为来自参数β（u）和ξ未知的广义帕累托分布的随机变量。为此，可建立样本对数似然函数：

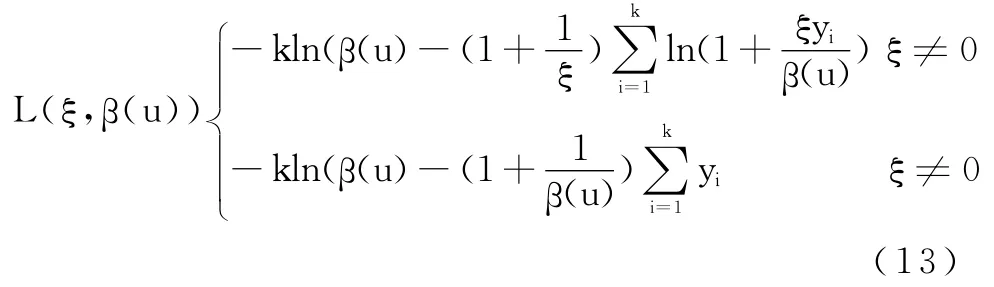
为估计损失分布的尾部，在等式（8）中令X＝y＋u；对足够大的阈值 u，我们有 Fu（y）≈Gξ，β（u）（y），并将其带入（8）式得：

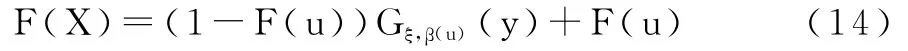
对（14）式的函数F（u），我们可用经验累计分布函数值F（u）＝（n-k）／n来替代（k代表超越阈值u的样本观测值个数），这样，我们可以得到：

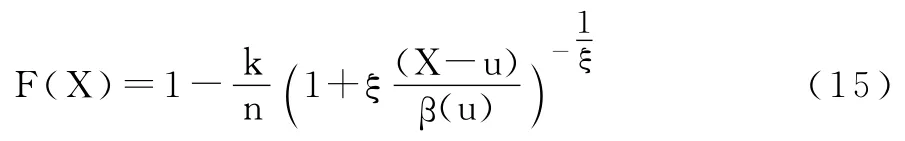
4.后验测试

为检验非交易风险计量模型的有效性，本文将分别对它们进行后验测试。所谓后验测试（Backtesting）就是用统计方法估算的数值结果对实际损失的覆盖程度。事实上，通过比较过去一段时间内期货收益的实际损失金额超过用模型估算的VaR值（或ES值）的次数（穿越次数）是否趋近于违约概率，来验证基于EVT的VaR（或ES）是否符合模型设定的违约概率，以此来检测所建模型的准确性。由此，各期货样本VaR（或ES）的溢出率为：

VaR（或ES）的E值将与设定的显著水平1-q相比较，进而来判断模型的准确性。当置信水平为q时，若E值大于1-q，说明非交易的风险水平较低；反之，若E值小于1-q，说明非交易的风险水平较高。总之，E值越是接近于1-q，说明模型建立得越准确。

四、实证研究

（一）数据选择

目前，我国期货市场上的主力期货品种包括上海期货交易所（SHFE）的铝、铜和橡胶、大连商品交易所（DCE）的大豆、郑州商品交易所（ZCE）的小麦（硬麦）。这些期货合约及其交易比较成熟，可以作为我国期货市场的代表。由于我国期货合约具有非连续的特点，因此，铝和铜选择3月期、橡胶选择2月期、大豆选择4月期、小麦选择2月期每个交易日开盘和收盘价格的连续数据［19］，其时间跨度为1995年6月1日至2009年6月30日，所产生的铝、铜、橡胶、大豆和小麦期货样本数据分别为3368、3432、2712、3263和2695个。期货价格数据来源于相应的期货交易所和国联倚天数据库。

表1 期货非交易收益的基本统计量① 类似于Tsiakas（2008）的贡献度检测和Granger因果检验，在5%的置信水平下，交易当晚、周末假日和中长假日的收益对传统收益和日间交易均具有显著影响；为保持论文的完整性和节省篇幅，对它们的论证则从略。

（二）非交易收益的基本统计特征

表1给出了非交易收益的基本统计量。可以看出，各期货合约不同时段的非交易收益均表现出不同的正、负收益特性，非交易收益的偏度也表现出不同的左偏和右偏特征；并且，各期货合约不同时段的非交易收益的峰度均大于正态分布的峰度3，由此说明各非交易收益均具有尖峰厚尾特征。从标准差来看，各期货合约交易当晚、周末假日和中长假日的标准差呈递增态势，这说明随着非交易时间的累积，非交易收益的风险会逐渐增大；且总体而言，铜、橡胶和小麦市场非交易收益的标准差较大，铝和大豆市场非交易收益的标准差相对较小。

（三）非交易风险的测度

1.阈值选择及分布参数估计

采用POT方法估计VaR与ES的值，先要确定阈值。从精度出发，各序列阈值的选取我们将结合平均剩余寿命图和观察不同阈值下参数的稳定性来共同确定。下图1给出了铝期货交易当晚、周末假日和中长假日收益序列的剩余寿命图及不同阈值下的参数变化图①铜、橡胶、大豆和小麦的图与此类似。。根据图1，我们可分别确定对应序列的阈值，然后再根据极大似然法估计对应序列的尺度参数和形状参数，表2给出了各期货不同非交易收益的阈值及尾部参数估计结果。

表2 各序列阈值及尾部参数估计值

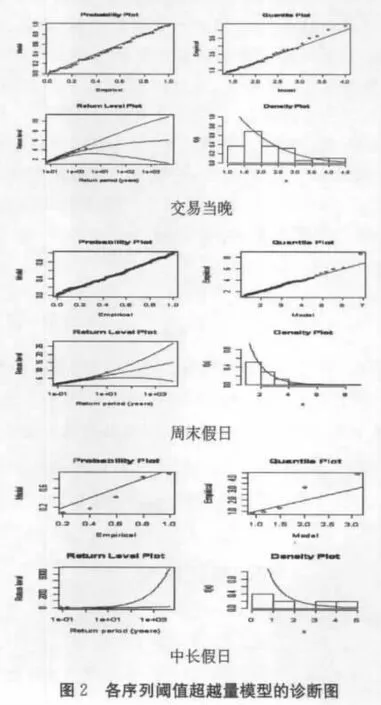
在确定损失的尾部极值分布时，我们常采用P-P图和Q-Q图来检验模型的拟合程度。为此，利用上文估计结果，我们可进一步得到各期货市场不同非交易收益序列GPD拟合的诊断图（如图2所示）。可以发现，所有的点都几乎在一条直线上，密度曲线的估计与直方图也相吻合，由此说明根据前文所提方法的参数估计是恰当的。

2.VaR与ES的估计结果

在满足上述假设的条件下，我们来估计95%和99%置信水平下的VaR与ES估计值。参数u、β、ξ估计出以后，利用（4）式和（7）式，即可计算出各期货市场不同非交易收益的风险价值（VaR）及其预期损失（ES）（以日作为持有期），并对其相应估计结果进行了后验测试（如表3所示）。

表3 各序列的风险价值及其预期损失估计值

表3给出了铝、铜、橡胶、大豆和小麦序列VaR和ES的估计值及其后验测试结果。根据后验测试结果可知，基于极值理论的VaR和ES模型可以比较好地描述期货市场非交易时段的风险价值及其预期损失。从纵向来看，对于每一期货交易品种，交易当晚、周末假日和中长假日的风险价值及其预期损失均呈递增态势。由此说明，我国期货市场非交易时间与非交易风险之间呈正向关系。也就是说，随着时间的累积，非交易时间的信息含量会逐渐增多，非交易风险也会随之增大，这也与前文非交易收益的标准方差具有递增特征相吻合。之所以出现这一状况，主要是于非交易时段所包含的大量私人信息和公共信息以及不同地区期货交易的非同步性有关［20，21］。这样，随着时间的延续，新信息积累到一定程度就会影响投资者的买卖行为，从而造成期货价格的波动［20］。一般而言，两个相邻交易日之间的非交易时间越长，累积的信息会越多，重新开盘时期货价格的波动也就越大，这就不可避免地导致期货市场非交易风险的增大。

从横向来看，在95%的置信水平下，铜和橡胶市场的非交易风险较大，小麦市场次之，大豆和铝市场相对较小；在99%的置信水平下，橡胶和小麦市场的非交易风险较大，铜和大豆次之，铝市场最小。总体而言，铜、橡胶和小麦市场的非交易风险较大，而铝和大豆市场的非交易风险相对较小，这与前文期货市场非交易收益的标准方差大小描述是相一致的。在非交易时段，不同期货市场非交易风险存在上述差异的原因有哪些呢？其缘由主要可归结为各期货市场非交易新信息在市场内部和市场外部的获取方面［22，23］。与前者不同，小麦市场相对狭小，市场也不太活跃；特别是作为标的物的小麦现货，长期受国家农业政策的制约和自然灾害的影响，等等。以上这些因素，会使得铜、橡胶和小麦期货在非交易时段的新信息累积相对较大，这自然加大了市场的非交易风险。然而，与铜、橡胶和小麦相比，铝和大豆期货及其现货的供需基本平衡，市场也较为成熟［23，24］，且相对而言，既存在较少的来自国外重大消息的影响，也较少受到来自国内经济政策等消息的冲击。总的来说，铝和大豆期货市场来自国内外新信息的累积相对较小，这也自然不会导致市场的大幅波动，因而非交易风险也比较小①事实上，不同期货市场的非交易风险存在个体差异的原因是非常多的，限于篇幅，这里只列出了几个较重要原因。。此外，置信水平的选择对风险价值及其预期损失的影响也是非常明显的，当置信水平从95%增加到99%时，风险价值增加了一倍以上，其预期损失增加了近两倍，这说明风险价值和预期损失对置信水平的选择非常敏感，预期损失比风险价值变化得更快，这也与风险价值和预期损失的理论定义相符。

五、结论与启示

本文在分析交易当晚、周末假日与中长假日收益基本统计量的基础上，系统测度了各期货市场不同非交易收益的风险价值及其预期损失。实证结果显示：（1）基于极值理论的VaR和ES模型可以较好地描述期货市场非交易时段的风险价值及其预期损失；（2）从纵向来看，交易当晚、周末假日和中长假日的风险价值及其预期损失均呈逐渐递增态势，这意味着我国期货市场非交易时间与非交易风险之间呈正向关系，即随着时间的累积，非交易时段的信息含量会逐渐增多，非交易风险也会逐渐增大；由此表明，非交易时段所积累的金融信息具有显著的预测能力。（3）从横向来看，在95%的置信水平下，铜和橡胶市场的非交易风险较大，小麦市场次之，大豆和铝市场相对较小；而在99%的置信水平下，橡胶和小麦市场的非交易风险较大，铜和大豆次之，铝市场最小。

以上研究结论有利于充分认识和把握我国各期货市场及不同非交易时段的非交易风险，以及非交易时间与非交易风险之间的正向关系，对我国期货市场投资者和风险管理当局来说均具有一定的实践指导意义。一方面，投资者可以利用非交易时间与非交易风险之间的正向关系来优化投资者的投资决策，可以利用不同期货非交易风险的差异性来规避非交易风险对期货交易的影响，还可以为期货市场的价格发现提供预测。另一方面，这一研究还可以为风险管理当局进行风险测度、风险管理制度的制定以及风险监管策略的设计等提供必要的方法和信息支持，期货市场管理者可根据非交易时段的长短有针对性地制定市场风险防控措施，为防范和化解非交易风险服务，实现期货市场非交易性风险的有效监管。

［1］Taylor N.A Note on the Importance of Overnight Information in Risk Management Models［J］.Journal of Banking and Finance，2007，31：161–180.

［2］Tsiakas I.Overnight Information and Stochastic Volatility：A Study of European and US Stock Exchanges［J］.Journal of Banking ＆Finance，2008，32：251–268.

［3］Baumol W.An Expected Gain-confidence Limit Criterion for Portfolio Selection［J］.Management Science，2008，10：174-182.

［4］Artzner P F，Delbaen J，Eber，Heath D.Coherent Measures of Risk［J］.Mathematical Finance，1999，9：203-228.

［5］Engle R F，Manganelli S.CVaR：Conditional Value at Risk by Quantile Regression［C］.NBER Working Papers 1999，No.7341，National Bureau of Economic Research，Inc.

［6］Manganelli S，Engle R F.Value at Risk Models in Finance［C］.Working Paper Series，No.075，European Central Bank，2001.

［7］Acerbi C，Tashe D.On the Coherence Expected Shortfall［J］.Journal of Banking and Finance，2002，26：1487-1503.

［8］Frey R，McNeil A.VaR and Expected Shortfall in Portfolios of Dependent Credit Risks：Conceptual and Practical Insights［J］.Journal of Banking and Finance，2002，26：1317–1344.

［9］Rockafellar R，Uryasev T S.Optimization of Conditional Value-at-risk［J］.Journal of Risk，2000，3：21-41.

［10］Tsay.Analysis of Financial Time Series［M］.John Wiley ＆Sons，Inc.2002.

［11］Longin F M.Optimal Margin Levels in Futures Markets：Extreme Price Movements［J］.Journal of Futures Markets，1999，19：127-152.

［12］迟国泰，王玉刚，汪红梅.基于多元GARCH-VaR的期货组合保证金模型及其应用研究［J］.预测，2008，27（5）：49-57.

［13］韩德宗.基于VaR的我国商品期货市场风险的预警研究［J］.管理工程学报，2008，22（1）：117-121.

［14］刘庆富，仲伟俊，华仁海，等.EGARCH-GED模型在计量我国期货市场风险价值中的应用［J］.管理工程学报，2007（1）：117-121.

［15］Rockafellar R，Uryasev T S.Conditional Value-at-risk for General Loss Distribution［J］.Journal of Banking ＆Finance，2002，26：1443-1471.

［16］Matthys G，Beirlant J.Estimating the Extreme Value Index and High Quantiles with Exponential Regression Models［J］.Statistica Sinica，2003，13：853-880.

［17］Balkema A，de Haan L.Residual Life Time at Great Age［J］.Annals of Probability，1974（2）：792–804.

［18］Pickands J.Statistical Inference using Extreme Order Statistics［J］.The Annals of Statistics，1975（3）：119–131.

［19］丁秀玲，华仁海.大连商品交易所大豆与豆粕期货价格之间的套利研究［J］.统计研究，2007，24（2）：55-59.

［20］French K，Roll R.Stock Return Variances：The Arrival of Information and the Reaction of Traders［J］.Journal of Financial Economics，1986，17：5–26.

［21］del Corral W，Colwell D，Michayluk D.News Releases when Markets are Closed［C］.Unpublished working paper，University of Technology Sydney，2003.

［22］Frank J F，Christopher K M，James E B.Holiday Trading in Futures Markets［J］.Journal of Finance，1994，49（1）：307-324.

［23］刘庆富.中国期货市场的隔夜信息能否影响日间交易价格——基于贝叶斯 MCMC推断的随机波动模型［C］.第八届中国金融学年会，山东大学，2011.

［24］Liu Q，Huang B，An Y.Risk contributions of trading and non-trading hours：Evidence from commodity futures markets［C］.Working paper，Fudan University and the University of Windsor.2010，12.