基于FPGA的数字下变频器设计

刘云龙，张伟霞

（1.广州海格通信集团股份有限公司，广东 广州510663；2.广州广电运通金融电子股份有限公司，广东 广州510663）

数字下变频技术在移动通信、数字广播、电视等领域具有重要应用价值。在接收机中，信号经混频后，输出到低通滤波器，滤除倍频分量和带外信号。但随着采样速率的提高，一个重要问题就是采样后的数据流速率很高，导致后续的信号处理速度跟不上，特别是对有些同步解调算法，其计算量巨大[1]。数据吞吐率过高很难满足实时性要求，因此有必要对A/D转换后的数据流进行降速处理。

数字下变频的基本功能是从输入的宽带高速数据流信号中提取所需的窄带信号，将其下变频为数字基带信号，并转换成较低的数据流[2]。高速ADC的输出信号送入至数字下变频器内，然后与数字本振正交混频，再经带通滤波器，滤除其他干扰信号，然后再进行信号的解调、解码处理。如果直接对混频后的数据进行带通滤波所耗费的运算量就特别大，例如信号的数字化采样率为30.72 MHz，滤波器为33阶FIR滤波器，则滤波操作需要1 013 M次乘法和980 M次加法，常规DSP难以承受。所以必须对混频后的信号进行降速处理，这就是下变频器主要完成的工作，如图1所示。

图1 数字下变频在接收机内的位置

1 原理实现

1.1 系统原理实现

数字下变频器输出信号的后续处理，主要是完成信号解调、解码、抗干扰、自适应均衡以及信号参数估计等工作[3]。由于正交分解后的I/Q两路基带信号对上述后续处理通常带来很大的方便和良好的性能，因此本设计采用了正交两路处理的典型结构。图2是本设计的结构框图。主要包括：数控振荡器、混频器、改进的级联积分梳状（MCIC）滤波器、半带（HB）滤波器、抽取器、可编程FIR滤波器、控制模块。

图2 数字下变频器结构框图

模拟中频信号由前端的模数转换器采样而得到数字中频信号，数字信号先与数控本振产生的两路正交本振信号进行混频，将数字中频搬移到基带。由于ADC在中频进行采样，采样速率有可能很高，而混频后得到的数据率和采样速率是一致的。如果直接利用FIR滤波器来实现的话，根本无法达到这个处理速率。因此混频后的信号先通过CIC滤波器和HB滤波器，然后进行抽取，降低数据率，再由FIR滤波器进行滤波。由于CIC滤波器的系数都为1，因此实现非常简单，只有加减运算，硬件实现时可达到较高的处理速率，适合作抽取系统中的第一级并进行较大倍数抽取的工作。但CIC滤波器阻带衰减的特性不是很好，通常需要采用五级CIC滤波器级联的方式加大阻带衰减，抽取因子为2～16。由于CIC滤波器的带内平坦度不是很好，因此在其后端加了一个补偿器，把它们合称为改进的CIC（MCIC）滤波器。HB滤波器由于其系数几乎一半为零，滤波时运算量减少一半，因此被作为第二级低通滤波器。HB滤波器处理后的信号的抽取因子固定为2，特别适合采样率降低一半的要求。通过MCIC滤波器和HB滤波器滤波抽取后，基带信号由最初的高数据率被降到较低的速率，适于后级FIR滤波器处理。

1.2 数控振荡器实现原理

数控振荡器是本地频振荡信号的发生机构。其功能主要是产生一个振荡频率为中频的理想正弦和余弦序列[4]。它是决定系统性能的最主要的因素之一。本文的数控振荡器采用直接数字频率合成技术来实现。

直接数字频率合成技术DDS（Direct Digital Frequency Synthesis）是从相位概念出发直接合成所需波形的一种新的频率合成技术。近年来，技术和器件水平不断发展，这使DDS技术也得到了飞速的发展，完成了频率合成技术的一次飞跃，是目前运用最广泛的频率合成技术。DDS的基本组成结构如图3所示。

图3 DDS组成结构

1.3 梳状滤波器实现原理

所谓积分梳状滤波器，是指其冲激响应有如下形式：

式中，D为CIC滤波器的阶数（D同时也是抽取因子）[5]，根据Z变换的定义，CIC滤波器的Z变换为：

它的实现结构如图4所示。可见，CIC滤波器由两部分组成，积分滤波器和梳状滤波器的级联。H1（z）为积分器是容易理解的，而称H2（z）为梳状滤波器，可以从它的幅频特性来说明。

图4 积分梳状滤波器的实现

1.4 半带滤波器实现原理

半带滤波器是系数特殊的FIR滤波器[6]。传统的FIR滤波器大都利用乘加器实现。一个N阶的FIR滤波器是由N个乘加器组成。每个乘加器包括：一个乘法器、一个数据寄存器、一个加法器、一个系数寄存器，还有级连的逻辑控制。在FPGA中，利用上述方法实现FIR滤波器是非常浪费资源和复杂的。本文采用分布式算法来实现FIR滤波器。分布式算法DA（Distributed Arithmetic）是一项重要的FPFA技术，广泛应用于计算乘加和之中。

如果滤波系数c[n]可以通过演绎得到，那么在技术上部分乘积项c[n]x[n]就变成一个常数乘法（也就是缩放）。这是一个重要的差别，也是DA设计的一个先决条件。为了理解DA设计范例，考虑乘积和内积如下：

这一步假设系数c[n]是已知常数，x[n]是变量。无符号DA系统假设变量x[n]的表达式如下：

其中xb[n]表示x[n]的第b位，而x[n]也就是x的第n次采样，而内积y可以表示为：

可以写成更为简洁的如下形式：

函数f（c[n]，xb[n]）的实现方法就是利用一个LUT实现映射。就是说2N字宽、预先设定的LUT接收一个N位输入向量xb[n]，输出为f（c[n]，xb[n]）。各个映射值都由相应的二次幂加权并累加。利用如图5所示的移位加法器就能够有效地实现累加，在N次循环后就完成了内积的运算[3-4]。

图5 移位加法器结构

1.5 可编程FIR整形滤波器实现原理

在数字下变频器的多级高效数字滤波器模块中，最后一级一般要使用可编程的FIR滤波器对整个信道进行滤波。信号经过前级的MCIC滤波器、半带滤波器抽取滤波后，输入到FIR滤波器的采样速率相对来说已经较低了，所以在能实时处理的前提下，可以适当提高滤波器的阶数。更高阶的FIR滤波器，能使滤波器的通带波动、过渡带宽、阻带衰减等指标能够设计得较好[7]。

该FIR滤波器的设计目标是尽可能地让期望信号通过，同时尽可能地抑制无用信号。对滤波器幅频特性而言，就是通带波动尽可能小、通带宽度尽可能与有用信号带宽尽可能一样、过渡带尽可能窄、阻带衰减尽可能大。本文所设计的可编程FIR滤波器是直接调用IP核来实现的，阶数为64阶，仍然采用串并结合的结构来实现。

2 系统的验证

本设计所选择的FPGA芯片为XILINX公司的VirtexII3000。芯片资源利用情况如表1所示。

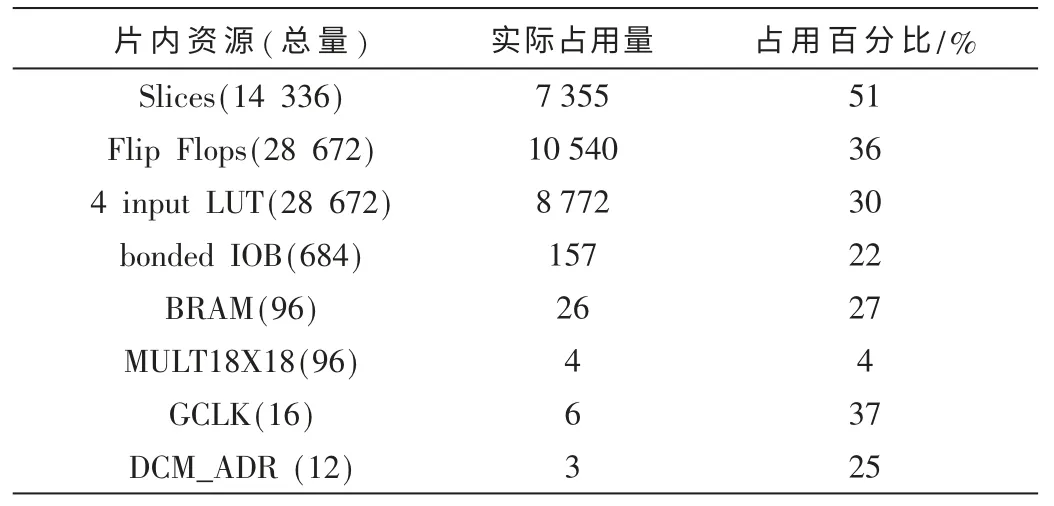
表1 系统总体性能情况表

选取输入信号为x=cos（2π （fc+f1）t+0.003 2cos2π（fc+f0）t），其中f1=0.3 MHz，f0=0.2 MHz，fc=30 MHz，选取的采样频率为fs=80 MHz，抽取系数CW1=4，CW2=4，CW3=1，即第一级CIC滤波器进行5倍抽取，第二级CIC滤波器进行5倍抽取，整个系统对其进行100倍抽取时，双路输出复信号的幅度频谱如图6所示。由频谱图可以看出数字下变频器的动态范围大于50 dB。

图6 正交两路合成信号幅度频谱

本文主要研究的内容是基于FPGA的数字下变频器的设计。首先根据客观要求和可用资源总数论证了数字下变频器整体的设计方案，然后根据设计方案将整个设计模块化，采用自顶向下的模块化设计的思想，完成各个模块的设计。通过配置各抽取引脚，可以实现8～1 024倍的抽取。最后以正弦信号为测试信号，测得系统的最大动态范围大于50 dB。

[1]杨小牛，楼才义，徐建良.软件无线电原理与应用[M].北京：电子工业出版社，2002.

[2]宋虎，陈建军.一种新的高效数字下变频方法及其FPGA实现[J].雷达与对抗，2006（2）：33-36.

[3]贾学琴，李强，王旭，等.数字下变频的FPGA实现[J].仪表技术与传感器，2006（1）：56-58.

[4]徐荣华，胡修林.基于多相滤波结构的宽带接收机数字下变频研究[J].计算机与数字工程，2003（35）：50-54.

[5]扬灵，吴黎晖，张蕴玉.基于高速抽取滤波器的数字下变频设计[J].华中科技大学学报（自然科学版），2006，34（6）：14-17.

[6]Mentor Graphics Corporation.HDL Designer Series Tutorials[M].Mentor Graphics，2002.

[7]徐光辉，汤磊.一种FIR滤波器的FPGA实现[J].电气电子教学学报，2001，23（3）：117-119.