GPS天线相位中心偏差的削弱方法

余龙飞,张姣姣,吴桂栋,陶庭叶

(1.合肥工业大学土木与水利工程学院,安徽合肥 230009； 2.安徽理工大学测绘学院,安徽淮南 232001)

GPS天线相位中心偏差的削弱方法

余龙飞1∗,张姣姣2,吴桂栋1,陶庭叶1

(1.合肥工业大学土木与水利工程学院,安徽合肥 230009； 2.安徽理工大学测绘学院,安徽淮南 232001)

在GPS单点定位中，接收机天线的相位中心的位置偏差会对定位精度产生一定的影响，而多种方法可以削弱此类影响。本文通过对相位中心偏差的直接改正、最小二乘改正以及残差和为零的最小二乘改正三种常用改正方法进行对比研究，结果表明应用残差和为零的最小二乘修正的定位偏移量最小，能更好地削弱天线相位中心偏差对定位精度的影响。

天线相位中心偏差；残差和为零；最小二乘

1　引 言

在进行GPS单点定位时,其测量的观测值是相对于GPS天线相位中心的,而实际的天线的相位中心(天线接收卫星信号的电气中心)和几何中心不完全一致,又对于不同频率的载波L1和L2,它们观测的相位中心位置也是不完全相同的。目前,天线相位中心偏差的削弱的方法主要有:一是检测GPS接收机天线相位中心偏差,一是把天线相位中心偏差作为未知数。前者在进行单点定位解算前需要测定天线相位中心偏差,后者在进行单点定位解算完成后再求解天线相位中心偏差进行平差[1]。

测量平差的模型大都是非线性的,而模型的理论闭合差均为零。在对非线性误差方程求解时均采用在未知参数的近似值按泰勒级数展开,并取至一次项,转化成线性误差方程,然后根据线性最小二乘准则构成线性对称法方程组,进行直接求解计算和分析平差结果。本文在对GPS观测数据单点定位解算后,根据天线相位中心偏差(PCO)求出对点位三维坐标的影响,引进一阶偏导数的非线性参数平差的近似直接解法与迭代解法基础上,提出附加残差和为零的条件,再次进行测量平差。对观测数据进行分析得到残差和为零的最小二乘能有效削弱天线相位中心偏差对定位精度的影响。

2　天线相位中心位置偏差的改正方程

单点定位解算后天线在地心地固系下的坐标为(X,Y,Z),接收机天线的载波L1和L2的相位中心在地心地固系下的坐标为(XL1,YL1,ZL1)和(XL2,YL2, ZL2),载波L1和L2天线相位中心偏差在地心地固系下的改正向量为(△XL1,△YL1,△ZL1)和(△XL2,△YL2,△ZL2),得出:

因此,接收机天线相位中心与卫星天线的相位中心的距离为:

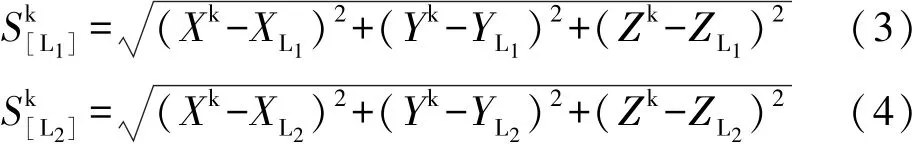
式中Xk、Yk、Zk为第k卫星的天线在地心地固系下的坐标。

为了处理数据的方便,将式(4)表示成天线的L1相位中心坐标的形式[1]:

式中,△XL1,L2、△YL1,L2、△ZL1,L2为天线的L1和L2相位中心之间的差异,即

3　残差和为零的非线性最小二乘回归

利用最小二乘回归,有截距的线性回归的残差和为零,无截距的线性回归和非线性回归的残差和通常不为零；残差和为零的非线性最小二乘回归之参数的精度高于普通非线性最小二乘回归参数的精度；对无截距的线性回归问题,通过附加残差和为零的强制条件后,参数的精度亦会提高[2]。

对于接收机天线相位中心与卫星天线的相位中心距离的非线性回归方程:

将式(7)简写为误差方程形式,111121212

应用高斯—牛顿法迭代求解载波L1和L2天线相位中心偏差改正后在地心地固系下的改正向量为

将式(8)在处展开并取一次项,得到线性化的误差方程:

从左到右依次记式(10)中的矩阵为v(r+1),B(r), δX(r+1),L(r),则可简写为:

v(r+1)=B(r)δX(r+1)-L(r)(11)

令:

利用式(11)构建强制条件附加残差和为零[2]:

将式(11)与(12)联立求解,根据附加限制条件的平差原理可重新求得:

其中NCC=CN-1bbCT。

用重新求得的δX(r+1)对非线性平差后(△XL1,L2,△YL1,L2,△ZL1,L2)(r+1)的进行改正,得消除模型闭合差后的解:

设因变量的观测值的个数为k,在附加强制条件后的标准差＾σ的无偏估计值为:

被估计参数(△XL1,L2,△YL1,L2,△ZL1,L2)的协因数阵Q为:

由于上式等号右边的第一项为非线性最小二乘平差后被估计参数的协因数,第二项大于零,因此附加残差和为零的条件后协因数阵Q变小,参数的估计精度有所提高。

4　数据分析

取多个GPS观测数据,采用精密星历对观测值进行单点定位解算时先不带入PCO值,待解算完成后基于非线性最小二乘和残差和为零的理论、利用精密星历和PCO值再次平差计算。其中观测值的权利用高度角定权[3]。表1、表2对一个观测数据单点定位两种方法求解的协因数和单位权中误差,表3对观测的多个单点定位解算利用三种方法解算的结果值比较。

两种方法求解的协因数 表1

两种方法求解的单位权中误差 表2

与已知坐标值的比较 表3

从解算结果可以看出:采用非线性最小二乘求得的参数协因数略小于残差和为零的非线性回归,协因数反映参数精度是非常有效的,并通过三种方法改正和已知坐标值对比,得到残差和为零的非线性回归的偏离量最小,因而残差和为零的非线性回归的精度高于非线性最小二乘。说明附加模型闭合差为零条件求得的参数精度高于普通最小二乘法计算的精度。

5　总 结

本文线利用附加残差和为零的条件,求得经残差和为零最小二乘改正的被估参数,对GPS单点定位解算后天线在地心地固系下的坐标进行改正,可以明显削弱GPS天线的相位中心偏差,从而提高测站坐标的解算精度,具有很强的实用性。

[1] 王雄，王建华，胡亚轩等.GPS高精度重复测量中的天线相位中心偏差检测及改正[J].内陆地震，2010，24(1)：31～36.

[2] 王仲锋，王琦.残差和为零的非线性回归法及其应用[J].东北林业大学学报，2011，39(2)：125～130.

[3] 高成发，赵毅，万德钧.GPS载波定位中双差观测值权的合理确定[J].测绘科学，2005，30(3)：28～32.

[4] 李征航，黄劲松.GPS测量与数据处理[M].武汉：武汉大学出版社，2005.

[5] M.Ge，G.Gendt，G.Dick，F.P.Zhang，and C.Reigber，Impact of GPS satellite antenna offsets on scale changes in global network solutions[J].GEOPHYSICAL RESEARCH LETTERS，VOL.32，L06310，doi：10.1029/2004 GL022224，2005.

[6] 高伟，晏磊，徐绍铨等.GPS天线相位中心偏差对GPS高程的影响及改正研究[J].仪器仪表学报，2007，28(9)：2052～2057.

[7] 涂锐，黄观文，邹顺.天线相位中心偏差变化及改正模型对精密单点定位精度的影响[J].大地测量与地球动力学，2010，30(3)：113～117.

[8] 易重海.实时精密单点定位理论与应用研究[D].长沙：中南大学，2011.

Weaken the M ethod of GPS Antenna Phase Center O ffset

Yu Longfei1,Zhang Jiaojiao2,Wu Guidong1,Tao Tingye1
(1.School of Civil and Hydraulic Engineering,Hefei University of Technology,Hefei230009,China；2.School of Prospecting and Surveying Anhui University of Science and Technology,Huainan 232001,China)

In GPS single point positioning,phase center offset of the receiver antenna has some influence on the precision of positioning,however,a fewmethods could weaken this influence.In this paper,three commonmethods that could weaken the influence are compared,including themethod of direct correction of the phase center,the least squares criterion correction and the least squares correction based on zero total residual difference.It is shown in the simulation that the positioning error achievesminimum under themethod of least squares correction based on zero total residual difference, therefore the influence on the positioning precision caused by phase center offset is better weakened.

antenna phase center offset；constraint of the sum of residuals is zero；least squares

1672-8262(2013)06-106-03

P228.4，P207

A

2013—03—08

余龙飞(1989—),男,硕士研究生,主要从事GPS精密定位。