基于时序植被指数数据的地表覆盖聚类分析研究

詹勇，马红，程方远

(1.重庆市勘测院，重庆 400020; 2.浙江省宁海县规划局，浙江宁波 315000)

1 引言

聚类分析就是用数学的方法处理给定对象的分类，已经被广泛应用到模式识别，数据挖掘，计算机视觉等领域［1］。随着遥感技术的发展，各种不同类型的传感器提供了大量的遥感数据，如何从海量数据中获取有用信息，聚类分析就是一种有效的方法，在土地覆盖分类、地物识别中起到了重要的作用。

上世纪70年代开始，科学家就开始研究并建立光谱相应与植被覆盖间的近似关系，在众多的植被指数中，归一化植被指数(NDVI)运用最多最广泛［2］。时序植被指数数据连续记录了植物生长变化的过程，通过对时序NDVI数据的分析有利于提高土地覆被分类的精度，因此时序NDVI数据的聚类分析研究具有重要的意义和应用价值［3，4］。

单独利用NDVI进行地表覆盖分类存在着较大的误差，近年来多时相数据在研究低分辨率土地覆盖和土地覆盖变化分析等方面引起许多研究者的兴趣，这些工作都是在强调利用植被指数的同时，或者引入其他的遥感观测数据［5］。Lambin和 Ehrhich提出 Ts/NDVI模型［6］，Ramakrishna Nemani和 Steve Running 利用NOAA/AVHRR多光谱遥感数据［7］;红波段，近红波段和Ts波段对美国进行土地覆盖覆被分类信息提取。随着遥感技术的发展和应用研究的深入，尽管许多新的植被指数考虑了土壤、大气等多种因素并得到发展，但是这些方法大都忽略了地表覆盖的持续动态变化，存在较多不可预测性误差。由于植被与非植被之间、各种不同的植被之间NDVI的变化曲线是不同的，所以可以利用季相性变化的NDVI指数，即时序NDVI来进行区域性地表覆盖分类或者提取土地覆盖的变化信息。本文是利用时序植被指数数据进行聚类分析，实验证明本文方法精度达到89.76%，高于传统聚类方法精度。

2 聚类分析原理与方法

2.1 聚类分析

聚类分析源于许多研究领域，包括数据挖掘、统计学、机器学习、模式识别等。它是数据挖掘中的一个功能，但也能作为一个独立的工具来获得数据分布的情况，概括出每个簇的特点或者几种注意力对特定的某些簇作进一步的分析。

聚类分析的输入可以用一组有序对(X，s)或(X，d)表示，这里X表示一组样本，s和d分别是度量样本间相似度或相异度(距离)的标准。聚类系统的输出时对数据的区分结果，即 C={C1，C2，…，Ck}，其中 Ci(i=1，2，…，k)是X的子集，且满足如下条件:

C中的成员C1，C2，…，Ck称为类或者簇。

2.2 K均值(K－means)聚类分析方法

J.B.MacQueen 在 1967 年提出的 k－means算法是到目前为止用于科学和工业应用的诸多类算法中一种极有影响的技术。它是聚类方法中一个基本的划分方法，本文讨论的是在误差平方和准则基础上的kmeans算法。

k－means算法又称硬 C－means(HCM)算法，能够对超椭球状的数据进行分类。属于动态聚类算法，理论上来讲，对于一个聚类命题，由于样本数目是有限的，可能的划分也是有限的，因而可以用穷举法来求解，但是对于大多数命题来说，穷举法是完全行不通的。设样本数为n，要求分为C类，则使每类不为空的划分大约有Cn/C!种，当n=100，c=5时，就有约1067种划分，因而实际采用迭代最优化的方法来求得最优划分。

已知样本集合 X={x1，x2，…，xn}，xk=(xk1，xk2，…，xks)T∈Rs，n 是样本个数，类别 c事先给定，mi⊂RS(1≤i≤C)是聚类原型模式或聚类中心，选择误差平方和准则函数最小为目标函数，如式(2):

式中n是总的样本数目。其中:

若xj离第i个类别的聚类中心最近，则μij=1，即xj∈Xi;否则 μij=0，xj∉X。

2.3 模糊C均值(FMC，Fuzzy C－Means)聚类分析方法

Dunn根据Ruspini定义的模糊划分的概念，把硬C均值聚类算法推广到模糊聚类情况，为了给隶属度函数一个权重，对隶属度函数进行了改进，把μij变成了，式(4)是模糊 C 均值(FCM，Fuzzy C－Means)算法的数学描述:

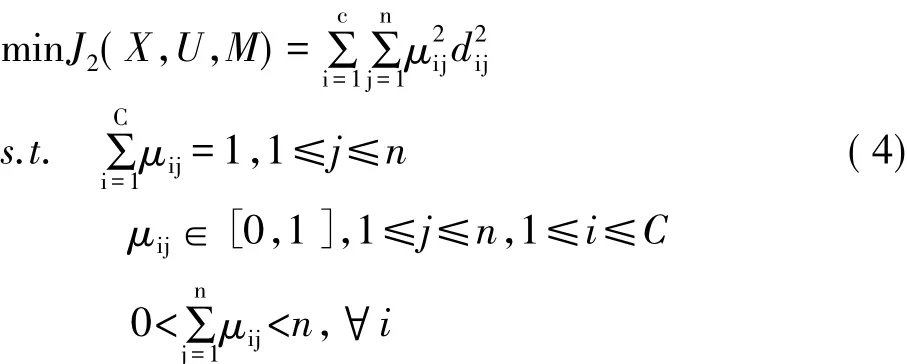
Bezdek把上述表达式推广到一般的情况，式(5)是 FCM 算法的描述［8］:

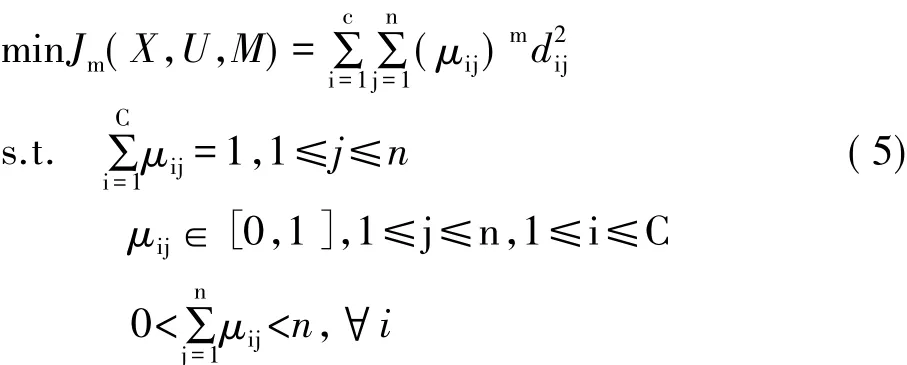
其中，m是模糊加权指数(m≥1)。

3 时序植被指数的聚类分析方法

3.1 时序NDVI信息

归一化差异植被指数(NDVI)产生于上世纪70年代，由Rouse提出，是遥感监测地面植物生长和分布的一种方法。定义如下:

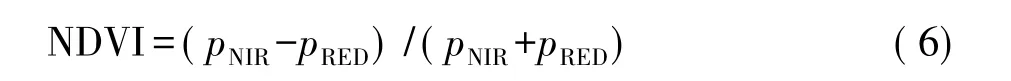
式中，pNIR代表红光波段、pRED为近红外波段。

季节性变化是土地覆盖最本质的特征之一，也是土地覆被状况的光谱特征表现，它是受气候、水文、土壤、高程等自然因子和人为影响而随时间变化的一种自然现象。鉴于植被与非植被之间、各种不同的植被之间NDVI的变化曲线是不同的，可以利用季相性变化的NDVI指数(即时序NDVI)进行区域地表覆盖分类。

3.2 时序NDVI特征提取

对于NDVI数据，用户信息提取的数据量一般很大，噪声影像严重，并且数据冗余;本文采用特征提取和特征选择的方式有效减少噪声、压缩数据。常用的NDVI时间分析方法包括:

(1)代数运算法。通过对NDVI时序数据直接进行代数运算提取特征，如变化幅度、变化均值等。

(2)线性变换法，通过线性变换方法，如主成分变换，缨帽变换等压缩高维信息，提取特征信息。

(3)时域－频率变换法。通过数据信号处理的方法，将NDVI时序数据构成的时序信号通过傅里叶变换到频率域中进行特征提取［9］。

3.3 基于时序NDVI的地表覆盖聚类分析

将原始数据进行实验裁剪和波段叠加等预处理，将数据进行主成分变换分析提取时序NDVI数据。在此基础上，分别采用K均值算法和模糊C均值算法进行聚类分析，对聚类结果进行整合，输出聚类结果，即可得到地表覆盖分类结果。算法实现流程如图1所示。

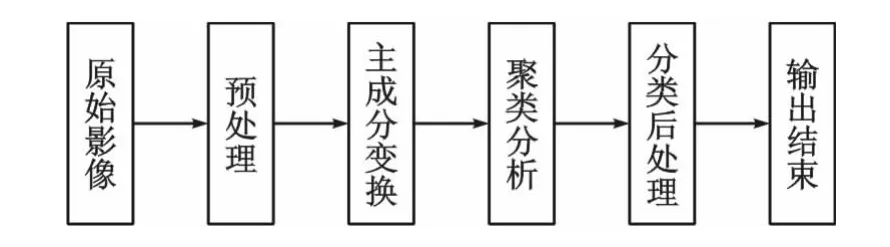
图1 时序NDVI数据聚类分析流程

4 实验分析与精度评定

本文实验数据是源于美国NASA Pathfinder ACHRR的中国卫星遥感植被指数(NDVI)数据集。该数据集包含一年内1月～12月三颗卫星，共12旬数据。图2为原始的帧影像，24位bmp图，其中R=B=G。

裁剪后的影像(共12幅，每月1幅)，用Erdas对其进行波段叠加;再对叠加后的影像进行主成分(PCA)变换，取前三位得到主成分变换图像，其中前三个波段的对数据集的贡献率分别为99.06%，0.4%，0.11%，总计99.67%，因而能代表12个波段数据。

图2 中国植被指数(NDVI)数据(其中一帧)

针对处理后的影像(时序NDVI数据)，分别采用K均值和模糊C均值方法进行聚类分析。聚类结果如图3所示。

图3 时序NDVI数据聚类结果

分别对K均值算法和模糊C均值算法聚类结果进行处理。借鉴IGBP的全球土地覆盖分类系统将初始聚类结果后处理为15类［10］。对比分析时，认为该分类结果中半灌木荒漠、沙漠及建筑用地与8类分类系统的裸地对应，典型草地及荒漠草地与草地对应，本文实验采用的数据集，图中DN值为1的是水体，已经被剔除，图例中给出7类，实际还有1类是水，共8类。处理结果如图4所示。

精度验证通常用外业验证或利用对应土地利用图完成，本文选取全国土地利用图来进行验证。分类对K均值算法和模糊C均值算法的聚类结果进行精度评定;同时将K均值算法和模糊C均值算法对单幅NDVI分类结果进行精度评定。采用随机抽样法分别抽取300个样本，计算他们的总精度和Kappa系数。表1所示的计算结果表明，利用时序NDVI对地表覆盖进行分类精度远高于直接利用单幅影像进行分类的结果，而且同类数据中，利用模糊C均值算法聚类的结果比K均值算法聚类的结果更好。

图4 聚类分析处理后的结果图

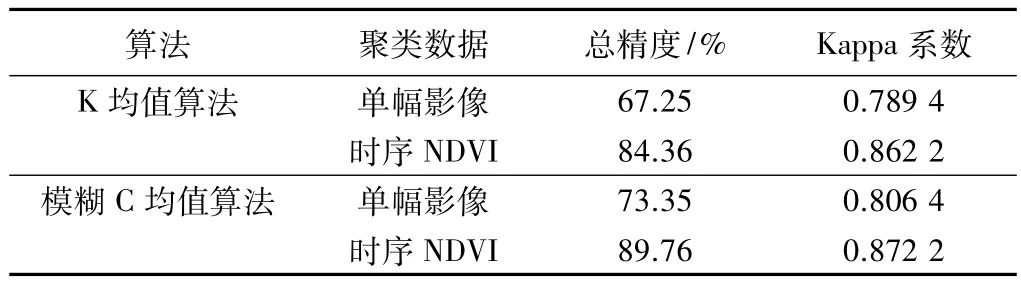
精度评定结果 表1

5 结论

通过本文利用不同的聚类算法对时序NDVI数据进行聚类分析，通过对实验结果进行分析，可得知经典的K均值算法和模糊C均值算法具有良好的特点，在影像聚类分割中具有很高的地位，由文中试验可以看出K均值算法和模糊C均值算法均能够得到较高的分类精度。

此外，本文利用K均值算法和模糊C均值算分别对单幅影像进行聚类分析，并将分类结果与时序NDVI数据聚类结果进行比较。可得知时序NDVI数据比单幅影像数据更能准确反映地表覆盖情况，时序NDVI数据分类结果远高于单幅影像分类结果。

［1］Pedrycz W.基于知识的聚类从数据到信息粒［M］.北京:北京师范大学出版社，2008.

［2］郭铌.植被指数及其研究进展［J］.干旱气象，2003，4(13):71～75.

［3］Viovy N.Automatic Classification of Time Series(ACTS):a new clustering method for remote sensing time series［J］.International Journal of Remote Sensing.200，7(6):1537～1560.

［4］刘庆凤，刘吉平，宋开山.基于MODIS/NDVI时序数据的土地覆盖分［J］.中国科学院研究生院学报，2010，2(27):163～169.

［5］程丽莉.基于时序NDVI的区域土地覆被分类方法探讨［D］.2007.

［6］Krishnapuram R，Keller J M.A possibilistic approach to clustering.［J］.IEEE Transactions on Fuzzy Systems.1993，2(1):98～110.

［7］R K，M A K J.The Possibilistic C－Means Algorithm:Insights and Recommendations［J］.IEEE Transactions on Fuzzy Systems.1996，3(4):385～393.

［8］孙茜，武坤.一种改进的可能性聚类算法及其有效性指标［J］.计算机工程与科学，2009，31(8):49～51.

［9］Lhermitte S.Hierarchical image segmentation based on similarity of NDVI time series［J］.Remote Sensing of Environment.2008，2(11):506～521.

［10］王长耀，骆成凤，齐述华等.NDVI－Ts空间全国土地覆盖分类方法研究［J］.遥感学报，2005，1(9):94～98.