灰色理论在大跨度连续梁桥线形控制中的应用

杨 惠

(中铁工程设计咨询集团有限公司 济南设计院，山东 济南 250022)

大跨度连续梁桥施工过程中重点和难点是线形控制，由于实际施工过程中受到诸多不确定因素的影响，使得施工各阶段理论计算值(如标高与内力)和实测值存在一定的误差，这些误差的存在可能导致桥梁合龙困难，影响桥梁安全性和美观性。通常将这些不确定因素看作为一种灰色量，采用灰色理论进行预测，在大跨度连续梁桥线形控制中具有一定的可行性。本文以京津城际铁路客运专线某大桥为工程背景，运用灰色理论建立模型，对桥梁施工过程中的标高进行预测，并和实测值进行对比分析，阐明了该法的可行性。

1 灰色控制理论

灰色系统理论特点是通过建立GM 模型加工处理原始数列数据，预测系统未来发展变化的一种预测控制方法。

GM(1，1)模型建立原理为:将原始数列X(0)= (X(0)(1)，X(0)(2)，X(0)(3)，…，X(0)(n))累加一次生成数列X(1)= (X(1)(1)，X(1)(2)，X(1)(3)，…，X(1)(n))、X(1)(k)=，其中，k = 1，2，3，…，n 。经过累加后，原始数列规律性增强。令X(1)的均值数列为Z(1)有Z(1)(k)= 0．5［X(1)(k)+X(1)(k -1)］=(Z(1)(2)，Z(1)(3)，Z(1)(4)，…，Z(1)(n))。建立GM(1，1)灰微分方程

式中，a 为发展系数;b 为灰色作用量;X(0)(k)为灰导数;Z(1)(k)为白化背景值。

其对应的白化微分方程为

当X(0)(1)= X(1)(1)时，其解为

利用最小二乘法解出(3)式参数向量

通过(4)式求得出a 与b 的值，代入到白化响应式可得到下阶段X(1)(n +1)，按照这样的方法依次，将得到的数列累减还原生成，求出还原模拟值是

从而求出下一阶段状态预测值。

2 灰色控制理论在工程中的应用

2．1 工程概况

京津城际铁路客运专线某大桥采用60 +100 +60 m 现浇连续箱梁，梁体为单箱单室，采用C50 混凝土。箱梁顶宽为13．4 m 的现浇梁。

京津城际铁路客运专线设计车速为350 km/h，梁体线形对行车的舒适性有较大影响。采用的博格板式轨道系统也对桥面的平整度要求较高，施工悬浇段按六面坡要求设置护面钢筋网片，桥面六面坡一次形成，需要在施工过程中严格控制桥面高程，这就需要在施工过程中对结构和挂篮的变形有准确的预测和细致的施工过程。

本桥线形控制的最终目标是:成桥线形与设计线形误差在+1．5 cm 和-0．5 cm 之间，合龙误差在1．5 cm 以内。在施工过程中采用如下措施控制误差:

(1)挂篮定位标高与预报标高之差控制在0．5 cm 以内。

(2)纵向预应力钢束张拉完后，如果标高误差超过±0．5 cm，则要分析误差原因，制定下阶段施工调整方案。

(3)特殊情况发生时，调整方案做相应的改变。

2．2 计算模型

依据设计文件、施工指导设计文件等资料，按照施工流程图对斜拉桥施工各阶段仿真计算，全桥共建76 个结点，75 个单元。有限元计算模型如图1 所示。

图1 计算模型

模型中66#墩设置固定支座，65#、67#和68#墩设置活动支座。

按照施工阶段划分情况对本桥进行了监控计算，结构自重系数、摩阻系数等参数按照设计所取，成桥运营阶段考虑收缩徐变1 000 d 后的梁体累计位移如图2 所示。

在1/2ZK 活载作用下，梁体竖向位移如图3 所示。

图2 成桥运营阶段累计梁体位移图

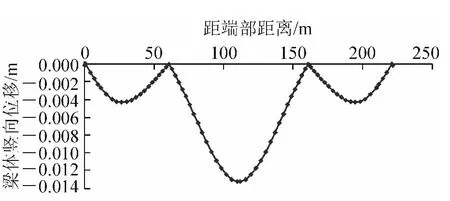
图3 1/2ZK 活载竖向位移图

2．3 立模标高的确定

确定立模标高计算公式为

式中，Hlmi为i 阶段立模标高;Hsji，∑f1i，∑f2i，f3i，f4i，f5i，fgl分别为i 阶段设计标高、本阶段以及后续阶段梁自重挠度总和、张拉本阶段及后续阶段预应力引起的挠度、混凝土收缩徐变引起的挠度、施工临时荷载引起的挠度、使用荷载引起的挠度的50%、挂篮变形值。

依据上述理论，得到各梁段的预拱度，梁体预拱度计算值如图4 所示。未考虑挂篮及支架变形，监控中将根据上一阶段的变形预测本阶段的挂篮和支架变形。

2．4 灰色预测系统在线形误差调整中的应用

通过有限元软件得到第 号梁段施工前已浇段挠度变化值，在第 节段浇筑后，测出前 节段挠度变化实测值。对挠度理论值与实测值建立误差序列作为原始序列，建立GM(1，1)模型。根据灰色原理编制了MATLAB 程序。

下面以节段是66#墩已施工完毕的第11 节段为例来说明灰色理论在预拱度误差调整中的的具体应用。采用新陈代谢模型确定第12 节段标高，以张拉后4 个理论挠度变化值与实测值的差值作为原始数据列建立灰预测模型如表1 所示。运用BSAS 软件进行正装分析得到张拉后理论上挠值数列为L = (L(1)，L(2)，…，L(k))，实测上挠度数列X = (X(1)，X(2)，…，X(k))，二者的差值即为原始数据列对应的误差数列为X = (X(1)，X(2)，…，X(k))。输入所编制的MATLAB 语言程序，计算得到第12 节段的上挠度调整值δs=2．0 mm。

表1 66#墩第11 节段施工完毕后理论、实测、调整数据表

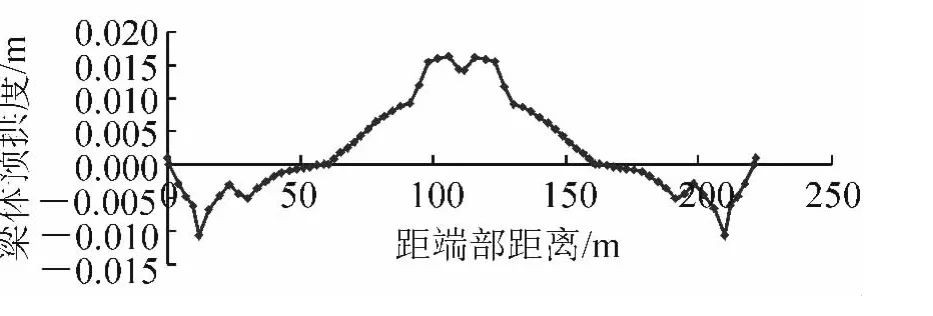
图4 梁体预拱度计算值

2．5 线形控制结果

中跨预应力束张拉后预拱度实测值与理论值对比图如图5 所示。

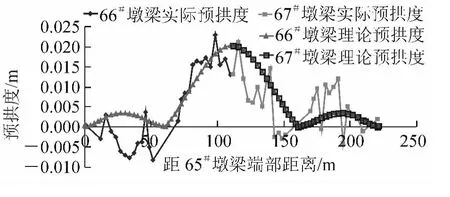
图5 中跨预应力束张拉后预拱度实测值与理论值对比

桥梁合龙后各节点标高实测值与设计值误差均在1．5 cm 以内，各合龙误差在1．2 cm 以内，梁体线形走势与理论线形一致，梁体线形平顺，满足控制目标要求。

3 结论

本文以京津城际铁路客运专线某大桥为工程背景，运用灰色理论建立 模型，在此基础上结合有限元软件对桥梁施工过程中的标高进行预测，并和实测值进行对比分析，通过以上分析可以得到如下结论:预测值和实测值吻合较好，达到了施工控制的目的。

(1)可行性。大跨度连续梁悬臂施工过程是一个非平稳的随机过程，可当作灰色过程，建立新陈代谢模型GM(1，1)，弱化了数据的随机性，凸现了该随机过程的规律性。通过上述工程实例分析表明，GM(1，1)能较好的预测大跨度混凝土连续梁桥混凝土浇筑与张拉前后的变形值。

(2)简便性。与建立有限元模型相比，GM(1，1)模型不必建立繁琐的程序，能很少的建立数据并实现数据的新陈代谢实时的反应施工状态。