星载激光测高仪回波信号仿真分析
2013-03-05朱近孙世君
朱近孙世君
(1南京理工大学 计 算机科学与技术学院,南京 2 10094)(2北京空间机电研究所,北京 1 00076)
1 引言
随着卫星测控技术的进步和成像系统性能的改进,测绘卫星的分辨率和水平测绘精度在不断提高。某些卫星的水平测绘精度可以达到米以下,但高程测量精度误差却很大。2008年发射的WorldView-2卫星其影像分辨率为0.46m,平面和高程精度为5m;2011年中国发射的“资源三号”卫星的正视全色影像地面像元分辨率为2.5m,有控制点情况下定标后高程精度达3m左右,无控制点定标后高程精度约为10m[1]。就当前的技术水平,通过视差图像计算得到高程,在地面控制点支持下精度在5m左右,而无地面控制点支持下的测量误差可达30m[2]。如何提高卫星测绘的高程精度,是一个急需解决而具有挑战性的课题。
激光测高是一种在地球科学和深空探测领域中有着广泛应用前景的新兴技术。相对于其它雷达高度计[2],激光测高仪具有方向性好、测距精度高的特点,在遥感、探测以及精确制导武器的跟踪制导领域体现出了巨大的应用潜力[3]。NASA于2003年发射的ICESat(Ice Cloud and land Elevation Satellite)卫星上搭载的地学激光测高系统[4-5],可用来测量冰盖高及其随时间的变化、云层和气溶胶的外形、陆地高和植被的厚度以及海冰的厚度等,测高分辨率为10cm,但在起伏地形情况下的误差大于10m。
将星载激光测高技术应用于测绘卫星,以提高高程测量精度是一种新颖的设想。定量研究不同的地形、地物对激光回波信号的变化状况和星载激光测高仪的实际测量精度等问题,是决定该项技术能否真正用于测绘卫星的可行性基础。
对激光脉冲的回波信号理论分析是激光测高技术的重要研究基础,文献[6]根据菲涅尔衍射理论对激光测高仪的回波信号表达式进行了推导。为了易于计算对模型目标做了简化,仅设置了3种(斜平面、阶梯和圆柱)地物模型,并忽略了表面微观粗糙度和噪声的影响。这种简化结果与具有随机起伏的自然地物的回波信号有较大的差异,不能直接用于实际地物目标的回波信号分析。试验研究是获取真实目标回波特征的有效方法,但要进行测量距离为数百千米的激光测高仪试验,不仅费用高昂、且试验环境难以设置。
用仿真技术模拟各种地物目标的激光回波波形,是全波形处理、目标回波特征提取等研究的重要手段[7],弥补了理论研究和实验研究的诸多不足。近年来,激光探测回波仿真技术已被应用于激光雷达系统设计[3]和激光雷达图像数值模拟[8];森林植被激光遥感数据反演研究等领域。
本文将采用计算机仿真技术对激光回波信号做定量研究。首先建立激光足迹区域的高精度立体地物数字模型、激光脉冲数学模型和噪声信号模型,并设计了针对光栅网格地形数据的网格节点激光回波近似算法,避免了经典算法中的三角面片划分、面片间遮挡测试和消隐处理,简化了模拟计算过程。对理想平面目标的激光回波仿真结果与理论结果一致。仿真程序在Matlab环境下开发和运行,可模拟多种参数条件下的激光回波信号,对星载激光测高仪在不同地物目标区域的回波信号进行了定量的研究与分析。
2 参数与模型
星载激光测高仪以脉冲方式工作,以测绘卫星为运行平台;其轨道运行高度与测绘卫星相同为500km,激光足印直径在30~50m。典型工作过程为:激光测高仪对待测区域发射一个激光脉冲,经过大气传输后一小部分激光被目标反射回测高仪。光电探测器件将探测到的激光回波转变为电信号,经采样得到激光脉冲回波的数字信号。通过测量光脉冲飞行时间可计算出精确的距离值,再结合测高仪平台轨道高度可得到目标地域的高度。
计算机仿真是一种通过建立与实际系统相符合的数学模型,再运用计算机进行仿真运行,以达到研究系统的目的。因此建立合理的数学模型与设计仿真程序是仿真研究的关键。
仿真系统由平台参数设置、地物参数设置、发射脉冲参数设置、接收机参数设置、激光回波信号仿真和系统主控6个功能模块组成。仿真程序的总体结构见图1。

图1 仿真程序总体结构Fig.1 Overall block diagram
2.1 平台参数设置
系统采用笛卡儿坐标系,见图2。激光测高仪位于卫星平台上,激光光束中心始终对准激光足迹区域中心。平台参数包括:位置(xp,yp,Hp) 和X方 向夹角 ;缺省值(与测绘星一致)为H=500km, =5?。(xp,yp,Hp)坐标可直接设置,或由(Hp,)根据激光足迹区域尺寸计算得到。

图2 坐标系统示意Fig.2 Coordinate system diagram
2.2 地物数字模型
地物模型由高程数据、漫射和反射参数组成;高程数据采用栅格结构。假设星载激光测高仪的激光足迹区域的缺省参数为30m×30m;与测绘星的像元分辨率一致,栅格尺寸ds=0.5m;栅格数目ms=60。
地物模型的数据由3个ms×ms的 矩阵构成:高程矩阵H={hi,j|i,j=1,2,3,…,ms},漫射系数矩阵A={ai,j|i,j=1,2,3,…,ms}和反射系数矩阵B={bi,j|i,j=1,2,3,…,ms} 。A、B的缺省值设为0.4和0.6。
地物高程模型采用笛卡儿坐标系描述,原点位于激光足迹区域的左下角,区域的高度差为hs(hs[-100m, 100m])。本文设计了3种地物模型:平面型、阶梯型和高斯(起伏)型。为了能更好的近似实际地物,所有地物模型上可加 [ 0,h]均匀分布的随机起伏。
(1)平面型
地物表面为理想平面,可沿X方 向、Y方 向或XY方 向倾斜,由预设高度差hs控制倾角。生成的模型见图3(a)。
(2)阶梯型
地物表面由np(np[1,4])个阶梯平面构成。各平面的面积相等,阶梯平面高程hi由 预设高度差hs均分得到:

生成的模型见图3(b)。
(3)高斯(起伏)型
地物表面也由np(np[1,4])个高斯曲面组成。高斯曲面的数学描述为:
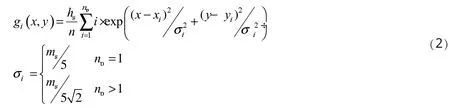
式中用 于控制高斯曲面形状,可以根据要求调整;(xi ,yi)是 曲面中心,根据不同的np在区域内均匀取值。生成的模型见图3(c)。
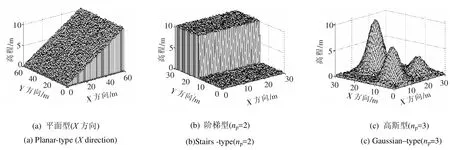
图3 地物模型(hs = 10m,∆h =0.5m)示意Fig.3 Terrain modelsdiagram(h s =10m,∆h=0.5m)
2.3 激光发射脉冲与接收机模型
激光发射脉冲信号能量是时间的函数,时间能量分布模型为[9]:= T

时间离散化为{ti=i×t|i=0,1,2,3,…,nt} ,其中nt是离散数量,t =2T1/2/nt是时间间隔。能量归一化后的离散激光脉冲如图4所示,图中tp为时间离散峰值点。

图4 激光脉冲时间离散示意Fig.4 Laser pulse time discrete diagram
激光束的空间能量在其横截面上的分布是非均匀的,能量分布取决于激光器的种类和光面形状。一般的发射激光束为基模光束。与常规雷达不同,基模光束的空域光强分布为高斯线形,按光束发散角度可表示为[7]:

式中I0为 中心处的光强;r为 目标距光斑中心的距离;R(z) 为 距离激光发射器z处的光斑半径,见图5。为简化计算将激光足迹定义为方形,区域中的激光能量分布如式(4)。

图5 激光能量分布示意Fig 5.Laser energy geometric distribution diagram
在数字仿真中涉及激光测高仪接收机的主要技术参数包括:
1)回波信号采样频率(fs) 。fs决定了激光测高仪的理论分辨率;在理想条件下,采样频率与距离测量分辨率d成反比:d =(C/fs)/2,C为光速。但在实际情况下,由于真实回波信号的复杂性和噪声的影响,单独提高采样频率并不能改进测量精度,且受到技术条件的限制,也不可能无限提高采样频率。设置采样频率的缺省值为fs=800MHz,d=0.187 5m。
2)测量范围与回波信号存储。测量范围指平台参数确定后,激光足迹区内可测量的高程的动态范围。当高程动态范围在[hmin,hmax]区间时,所需要保存的最小采样信号数目Imax为:

设立具有Imax个元素的Echo_data数组来保存模拟回波信号,初值设置为0。其回波时间与数组下标i(i∈[1,Imax])的换算关系为:

式中ti为时间离散后的第i个子脉冲时间;表示向下取整。数组下标i与高程hi的换算:

由于显示结果时所关心的是有效回波信号,因此需要自动确定回波信号大于零的下标区间进行显示;而不需要显示整个Echo_data数组的数据。
3 回波信号仿真计算
常规的激光回波信号仿真计算步骤为[8]:
1)搜集目标的三维结构资料,建立目标模型的三维几何模型;
2)对目标模型进行几何校正,并对面元进行细分,得到以三角面元形式的数据;
3)分析目标各面元之间的位置关系,以判断其是否被入射激光束照射,目标各部分之间是否存在遮挡。
4)对激光脉冲做空间和时间离散,分解成激光子光束组;
5)假定光斑内目标为漫反射目标,服从朗伯余弦定律,分别计算各激光子光束在目标对应小面元上的回波功率密度;
6)对所有激光子光束的回波信号进行积分,模拟得到对整个目标的回波信号。
其中步骤2)、3)是常规方法处理回波仿真计算的关键和难点,涉及到目标的结构、激光的入射方向和目标的姿态等。需要利用计算机图形学的消隐算法实现遮挡消隐判断,算法复杂,计算量大。
3.1 激光脉冲回波信号近似算法
针对特定目标的高程栅格数据,设计了激光脉冲回波信号近似算法,直接利用高程栅格数据按距离加权近似计算激光子光束与目标的交点与交角;避免了目标表面三角分割、表面遮挡等复杂计算,得到了良好的结果。具体的步骤如下:
1)根据相邻高程栅格数据(H)计 算描各网格点的单位法向矢量(n ij):

式中i,j=1,2,3,…,m。
2)离散化激光光束。在空间上将激光束分解为m2条 独立的子光束 {Lk| k=1,2,3,…,m2},它们分别照射在激光脚印的不同采样区内,即坐标点{(i×ds,j×ds, 0) |i,j =1,2,3,…,m}。在 空间上将激光脉冲离散为nt个独立的理想脉冲(如图6)。
3) 为描述简单,将2维数组下标(i,j) 转 换为1维下标p=(i-1)×m+j表 示;计算每条Lk与高程栅格点{hp|p=1,2,3,…,m2} 的 距离kp, 保 存kp≤ds/2且 高程值最大的1~3个相邻高程栅格点集合:Hg={(hq,q)|q=1,q=2,q=3} 作 为与Lk近似相交的地物区间。
4)用Hg中 网格点的单位法矢{n q}, 加 权平均计算与Lk近 似交点的单位法矢n p:

式中 为一小正数,避免分母为0时不能计算kq。

图6 激光束离散化示意Fig.6 The laser beam discretization diagram
5)计算Lk光 束在时间离散脉冲为l(l∈ [0,nt-1])的回波信号。假定光斑内目标为漫反射目标,服从朗伯余弦定律,信号衰减是常数因子,则子光束的回波信号的相对强度Eecho和 时间techo可表示为:

其中,子光束的相对空间能量Is(k) 按 式(4)计算;p(tl) 是 第l个 时间离散脉冲的相对能量;Rk是子光束与高程栅格点集合(Hg) 的 平均距离;a k′,bk′分别表示转换为1维下标后的漫射与反射射分量系数;φk为子光束入射方向与目标散射面法向n p的 夹角。将计算结果中的techo用 式(6)转换为下标i,Eecho累 加到数组Echo_data(i)中。
6)对空间离散后的m2条 子光束 {Lk| k=1,2,3,…,m2}分别进行3)、4)步骤计算;再令l=1,2,3,…,nt重复步骤5)计算总体回波信号。
最后结果保存在Echo_data数组中。用式(7)将回波时间转换为高程。
3.2 噪声模拟
由于一般星载的激光测高仪所测距离比较远,发射功率不是很大,加之远距离传输过程中信号干扰现象严重,导致回波信号很微弱,而且淹没在很大的背景噪声之中[10]。影响激光测高仪的噪声来源很复杂,主要有:太阳、大地以及其它辐射源的辐射进入接收视场引起的背景噪声,光电探测器固有的散粒噪声 (Shot Noise)、热噪声(Thermal Noise)、产生复合噪声(Generation Recombination Noise)及电流噪声等构成探测器噪声[11]。接收机输出的有效信号不仅受噪声的影响,还与发射脉冲能量、激光波长、光斑区域地物的漫射/反射特性、接收望远镜面积、测量距离、大气衰减、接收机灵敏度等参数相关。为简化仿真计算,采用接收机信噪比(SNR)参数来统一处理。
经探测器后的输出信噪比定义为信号的峰值功率与噪声功率之比的均方根值。信号峰值功率通过对理想的零高差平面(h=0m,hs=0m)地物模型仿真计算回波信号得到。
4 激光回波信号仿真实验与分析
为定量研究不同地形条件下激光测高仪的回波信号,及不同噪声水平对回波信号的影响,用上述的算法进行仿真实验。基准实验条件和参数包括:
1)平台参数。同2.1节说明。激光中心光束中心对准激光足迹区域中心;Hp=500Km,=5?。
2)地物参数。假设激光足迹为矩形,区域面积30m×30m;栅格尺寸ds=0.5m; 栅 格数目ms=60。平均高程由激光脚印区地物数字高程数据直接计算得到,可以作为实验真值。
3)激光发射脉冲信号。T1/2=4ns,(时间)离散数量nt=9。
4)接收机参数。回波信号采样频率fs=800MHz,高程动态范围±100m。
5)回波信号。为了显示直观,横坐标回波信号的时间按式(6)和式(7)转换为高程测量结果。结果参数:
最大值——接收机获取的回波信号最大(峰值)点的相对能量值;
峰值高程——回波信号峰值点对应的高程值;
中值高程——回波信号宽度1/2位置点对应的高程值。
4.1 地形变化对激光回波信号仿真实验
对平面型、阶梯型和高斯(起伏)型3种典型地物模型,分别进行高程差、随机起伏、阶梯平面/高斯曲面数量的参数变化实验。实验参数和数值结果见表1-3。
(1)平面型地形变化对激光回波信号影响的仿真实验
平面型地形仿真实验的参数和数值结果见表1,模拟回波信号如图7。

表1 平面型地形变化影响激光测高误差仿真实验Tab.1 Simulation of effects of plane terrain change on laser altimetry error
表1中平面地物的高程差按XY方向变化。峰值高程误差=峰值高程-平均高程,中值高程误差=中值高程-平均高程。

图7 平面型地形变化影响激光回波信号仿真Fig.7 Simulation of effectsplane terrain change on laser echo signals
(2)阶梯型地形变化对激光回波信号影响的仿真实验
阶梯型地形仿真实验的参数和数值结果见表2,模拟回波信号如图8。

表2 阶梯型地形变化影响激光测高误差仿真实验Tab.2 Simulation of laser altimetry errors affected by stairs terrain change
表2中阶梯高程为地物设置的阶梯平面高程,由式(1)计算得到。阶梯高程误差=峰值高程-阶梯高程。

图8 阶梯型地形变化影响激光回波信号仿真Fig.8 Simulation of laser echo signals vary with the stairs terrain change
(3)高斯(起伏)型地形变化对激光回波信号影响的仿真实验高斯(起伏)型地形仿真实验的参数和数值结果见表3。
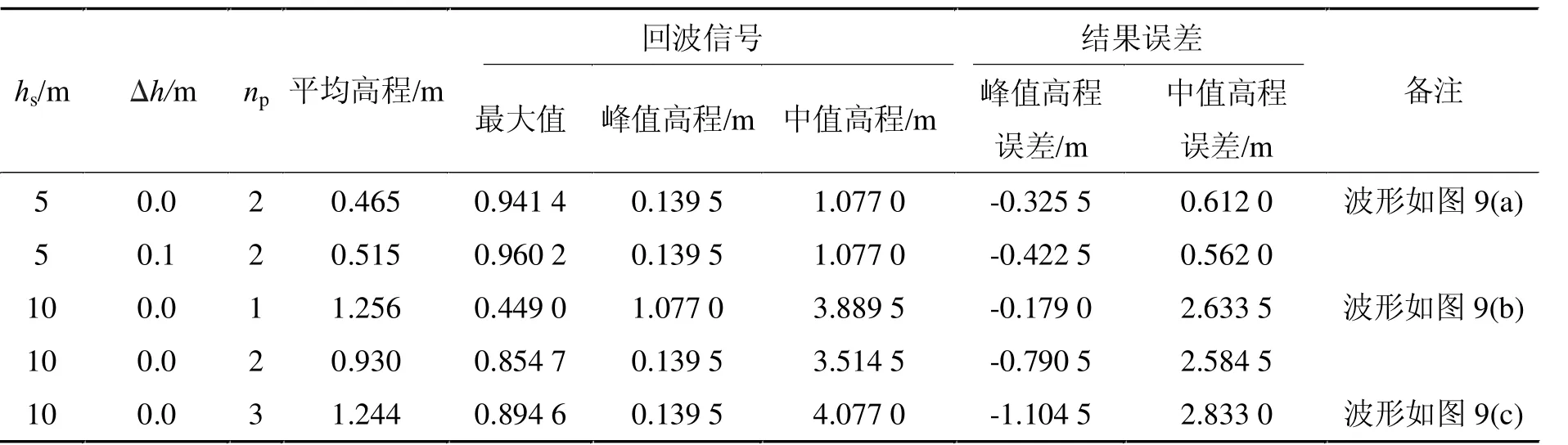
表3 高斯(起伏)型地形变化影响激光测高误差仿真实验Tab.3 Simulation of laser altimetry errors affected by gaussian wave terrain change
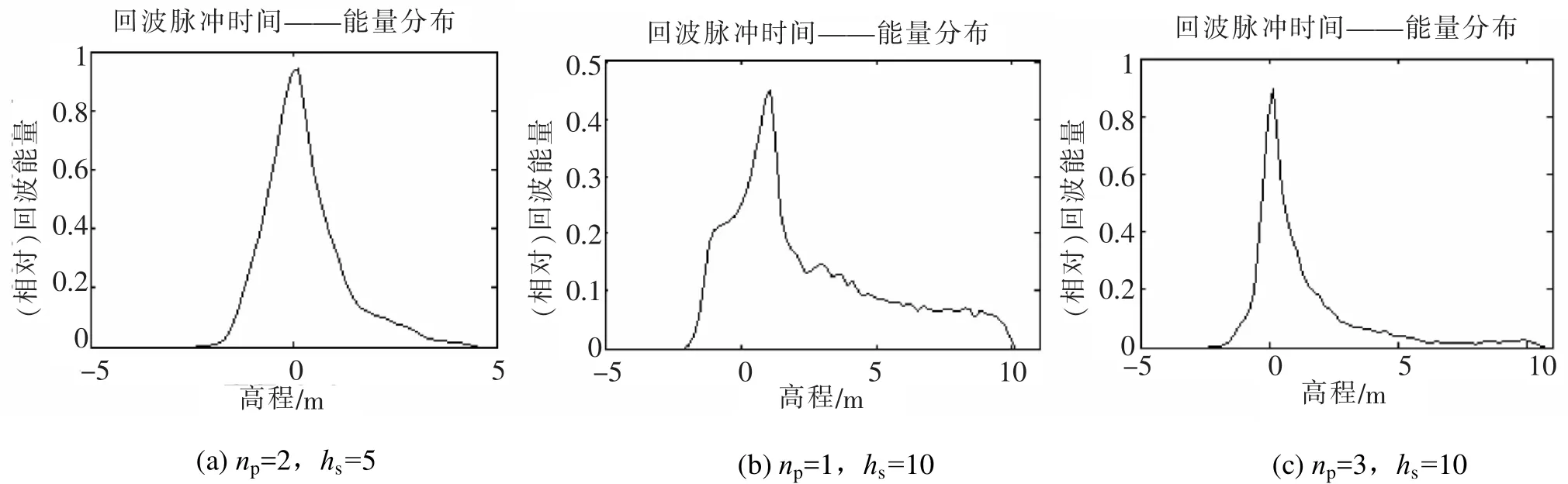
图9 高斯(起伏)型地形变化影响激光回波信号仿真Fig.9 Simulation of laser echo signalsaffected by gaussian wave terrainschange
4.2 信噪比对激光回波信号影响仿真实验
阶梯型地物(np=3,h=0.5m,hs=10m)理想回波信号如图10(a),加上信噪比SNR=5dB和2dB的模拟高斯白噪声后的效果见图10(b)和(c)。使用阶数order=20、相对频率fNy=0.2的FIR(Finite Impulse Response)低通滤波器,对有噪声信号(图10(b)、图10(c))处理后的结果如图10(d)和(e)。
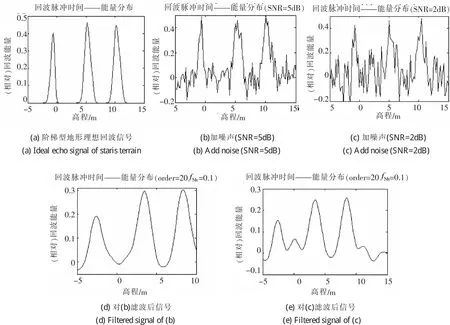
图10 信噪比变化对激光回波信号影响仿真实验Fig.10 Simulation of laser echo signalsaffected by SNRchange
4.3 结果分析
通过上述仿真实验分析,可以从如下方面得出相应结论:
1)理想平面型地形回波信号特点。回波信号呈单峰、对称形状(见图7)。随高程差hs的增加,即激光束与地面法向交角的增加,回波信号的峰值能量减小,信号宽度增加;与激光回波理论模型[5]计算的结果一致。地面上的随机起伏对回波信号的影响不大;当 时,峰值高程与测量光斑区域平均高程的误差小于0.5m;在hs时,中值高程与测量光斑区域平均高程的误差也小于0.5m。
2)理想阶梯型地形回波信号特点。回波信号呈多峰、对称形状;波峰数量与光斑区地物的阶梯数对应(见图8)。伴随阶梯高程差与波峰间的距离成正比,回波信号的峰值能量与各阶梯的有效面积相关。与激光回波理论模型[5]计算的结果一致。地面的小随机起伏(h<0.1m ) 对 回波信号的影响不大。在hs≤20m时,可用回波峰值所对应的阶梯高程来测量光斑区域的各阶梯平面高程,其最大误差在0.6m左右。
3)理想高斯(起伏)型地形回波信号特点。回波信号呈单峰、非对称形状(见图9)。回波信号形状与光斑区域的高程分布相关,但信号峰值与hs的相关性很小。地面上h<0.1m的随机起伏对回波信号的影响不大;当hs>5m时,峰值高程、中值高程与平均高程的误差可达到数米,因此不能直接用峰值高程、中值高程结果来修正光斑区域的平均高程。
4)信噪比对激光回波信号影响。当信噪比=2dB时,噪声对回波信号的影响比较大(见图10(c)),通过低通滤波器处理可得到较好恢复。滤波后的信号仍有失真(出现多个小干扰峰值),但3个有效回波峰值的相对能量远高于干扰值(见图10(e))。
在信噪比≥5dB条件下,噪声对回波信号的影响比较小(见图10(b)),用目视方法仍可以分辨回波峰值信号。使用低通滤波器处理可恢复得到很好的回波信号(见图10(d)),但处理后的信号会产生时间延迟,需要对高程测量结果进行修正。
5 结束语
本文通过建立地物数字模型、激光脉冲数学模型、接收机数学模型、噪声信号模型,设计了针对网格地形数据的激光回波近似算法,简化了仿真模拟计算过程。就3种典型地物模型,用数字仿真方法对星载激光测高仪进行模拟实验的结果表明:对理想平面和阶梯类型地物目标的测量精度可达到0.6m,可以用来校正立体测绘结果;而对高斯起伏类型地物目标不能直接使用其高程测量结果。
在回波信号中消除噪声信号技术,以及在高斯起伏类型地物目标回波信号中将有效信息用于校正立体测绘结果的方法,是后续进一步研究的目标。
(References)
[1] 李德仁,王密.资源三号卫星在轨几何定标及精度评估[J].航天返回与遥感,2012,33(3):1-6.LI Deren,WANG Mi.On-orbit Geometric Calibration and Accuracy Assessment of ZY-3[J].Spacecraft Recovery&Remote Sensing,2012,33(3):1-6.(in Chinese)
[2] 赵利平,刘凤德,李健,等.印度测图卫星IRS-P5定位精度初步研究[J].遥感信息,2007(2):28-32.ZHAO Liping,LIU Fengde,LIJian,et al.Preliminary Research on Position Accuracy of IRS-P5[J].Remote Sensing Information,2007(2):28-32.(in Chinese)
[3] 胡以华,舒嵘.机载与星载激光探测技术及其应用[J].红外与激光工程,2008,37(S):8-13.HUYihua,SHURong.Airborneand Spaceborne Laser Sounding Technology and Application[J].Infrared and Laser Engineering,2008,37(S):8-13.(in Chinese)
[4] 范春波,李建成,王丹,等.激光高度计卫星ICESAT在地学研究中的应用[J].大地测量与地球动力学,2005,25(2):94-97.FAN Chunbo,LIJiancheng,WANG Dan,et al.Applications of Icesat to Geoscience Research[J].Journal of Geodesy and Geody Namics,2005,25(2):94-97.(in Chinese)
[5] Zwally H J.ICESat’s Laser Measurements of Polar Ice,Atmosphere,Ocean,and Land[J].Journal of Geomatics,2002,34:405-445.
[6] 李松,周辉,石岩,等.激光测高仪的回波信号理论模型[J].光学精密工程,2007,15(1):33-39.LISong,ZHOU Hui,SHIYan,et al.Theoretical Model for Return Signal of Laser Altimeter[J].Optics and Precision Engineering,2007,15(1):33-39.(in Chinese)
[7] Steinvall O,Chevalier T,Larsson H.Data Collection and Simulation of High Range Resolution Laser Radar for Surface Mine Detection[J].Proceedingsof SPIE(S0277-786X),2006,6214:85-102.
[8] 李磊,胡以华,王恩宏,等.激光探测目标回波仿真技术研究[J].红外与激光工程,2010,39(Supplement):115-119.LILei,HU Yihua,WANGEnhong,et al.Study on Laser Return Waveform Simulation[J].Infrared and Laser Engineering,2010,39(Supplement):115-119.(in Chinese)
[9] 闫小伟,邓甲昊,孙志慧.脉冲激光成像探测系统回波信号仿真[J].光电工程,2009,36(12):42-46.YAN Xiaowei,DENG Jiahao,SUN Zhihui.Simulation of Echo Signal in Laser Imaging Detection System[J].Opto-Electronic Engineering 2009,36(12):42-46.(in Chinese)
[10] 荣雅君,王健,赵杰,等.星载激光测距仪回波弱信号检测技术研究[J].计算机与信息技术,2009(5):12-14.RONG Yajun,WANG Jianm,ZHAO Jie,et al.Research of Echo Weak Signal Detection Technology in Spaceborne Laser Rangefinder[J].Computer&Information Technology,2009(5):12-14.(in Chinese)
[11] 陈金令,谢德林,陈洪斌,等.激光雷达系统建模与仿真设计[J].计算机测量与控制,2007,15(12):1748-1749,1755.CHENJinling,XIEDelin,CHEN Hongbin,et al.Design of Simulation Software for Lidar System[J].Computer Measurement&Control,2007,15(12):1748-1749,1755.(in Chinese)
