基于噪声源估计的电机故障诊断研究

2013-03-04梁国荣谷爱昱沈训欢

防爆电机 2013年4期

梁国荣，谷爱昱，沈训欢

(广东工业大学自动化学院，广东广州510006)

0 引言

电机是当前应用最广的供电设备和驱动装置，其应用广泛、使用环境各异、负载性质不尽相同，这使得电机故障时有发生，在一些运行环境恶劣、负载冲击性很大的场合中运行的电机故障率更高［1］。电机常见的故障特征值最明显地表现在振动信号频率上，振动信号能很好地反映电机的运行状态，但振动信号采集条件偏高，不适宜一般性监测。

由于吸声率低，电机运行时机壳几乎毫无保留地对外辐射振动噪声，其噪声数据中必然携带着电机自身的结构信息和运行的状态信息。

本文基于声音阵列信号作为电机运行时发出的声音监测，为电机故障提供一种非接触式的诊断方法，而且采集到的噪声信号并不需要太长，一个有限时间内的记录就可以满足分析要求。将采集到的声音阵列信号放大并在Matlab 软件上进行数字滤波，通过盖氏圆算法确定噪声源数目并进行高分辨率谱估计算法(MUSIC 算法)分析，最后对电机进行故障诊断。

1 声音接收阵列信号模型

1.1 麦克风阵列信号采集处理特点

与传统的阵列信号相比，麦克风采集的声音阵列信号应注意［2］:(1)声音信号是宽带的，传统的阵列信号只适用于窄带上;(2)声音信号是短时平稳的，声音信号分析处理时要建立在短时基础上;(3)环境高混响及复杂噪声，在封闭环境中大量反射声波将造成高混响，背景噪声和噪声源也会降低声音信号质量。

针对以上特点，本文在测量数据时确保在大空间环境内减少混响与环境差异造成的背景噪声，免得造成声源质量的下降，同时对声音数据进行数字滤波，使得声信号在满足的窄带范围内进行数据处理分析。

1.2 麦克风传感器阵列

本文采用均匀线阵，设有m 个声探测器，有k 个声源信号，则阵列输出信号的向量可以表示为

式中，X(t)—阵列的M×1 维快拍数据矢量;N(t)—阵列的M×1 维噪声数据矢量;S(t)—空间信号的N×1 维矢量;A—空间阵列的M×N 维流型矩阵。

对于宽带信号，如果将观察时间T 分为K 个字段，每段时间为Td，然后对观察数据进行J 点的离散傅立叶变换(DFT)，只要子段Td相比信号和噪声相关时间较长，就可以得到如下的宽带模型［3］式中，Xk(fj)，Sk(fj)，Nk(fj)—为对应某频率的接收数据、信号及噪声的DFT 变换，其中k=1，2，…，K，j=1，2，…，J。

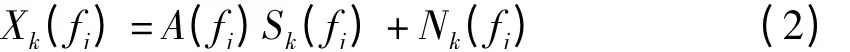
2 声音信号处理分析

电机发生故障时，例如旋转过程中的转子不对中，轴承外圈有磨损等都会产生周期性的冲击，此时冲击反应将对外辐射噪声，这些噪声带有的频率即为故障特征频率。由于冲击力带有宽带性质，特征频率从故障发生时到传感器接收信号已经产生衰减，因此对声音信号进行包络谱分析十分重要［4］。

2.1 Hilbert 变换

变换具体实现步骤如下:(1)对x(t)对作正傅立叶变换得X(f);(2)X(f)的正频率部分乘以-j，负频率部分乘以+j，经过这样的移相之后得到X^(f);(3)对X^(f)做逆傅立叶变换得x^(t)。

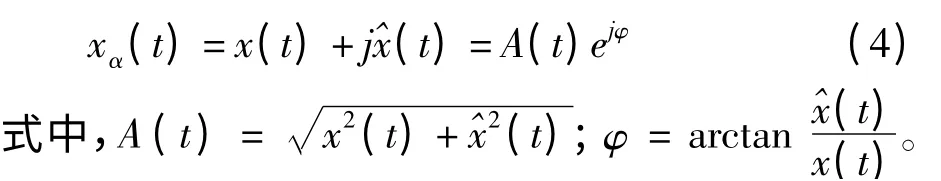
2.2 盖氏圆源数估计算法

盖氏圆定理就是将接收到的阵列协方差数据矩阵进行一定的变换，矩阵变换后信号圆半径和噪声圆半径就会分开，这时就可进行信号源数目估计［5］。

设有一N×N 维矩阵R，其第i 行第j 列的元素为rij，令第i 行元素(除第i 列元素)绝对值之和为

定义第i 个圆盘Oi上的点在复平面上的集合如式(6)表示

这个圆盘Oi称之为盖氏圆盘。盖氏圆盘定理已经被证明矩阵R 的特征值包含在圆盘Oi的并区内。这个圆盘的中心位于rii处，半径为ri(称之为盖氏圆半径)。

将噪声圆盘和信号圆盘分开可采用酉变换矩阵的方法，将取样协方差矩阵R 分解为方块阵，即

式中，RN-1—R 中除末行末列的子矩阵。再对RN-1进行特征值分解得式中，UN-1—RN-1的特征矢量构成的酉矩阵。利用UN-1构成一个酉变换矩阵T

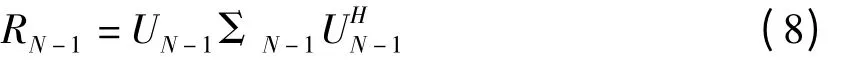
式中，N—各次快拍得到的信号协方差矩阵作平均来逼近RT的快拍数;D(N)∈［0，1］—N 的递减函数，需要根据具体情况设定。如果当k=k0时，GDE(K0)为第一个比0 小的值，则信源数的估计值取k0-1。

2.3 MUSIC 算法

只有正确地估计信号源数才能有效地获取信号源方向，由盖氏圆算法确定信号的振源数目后便可进行高分辨率多重信号分类(MUSIC)算法［6］。设阵列数据的协方差为

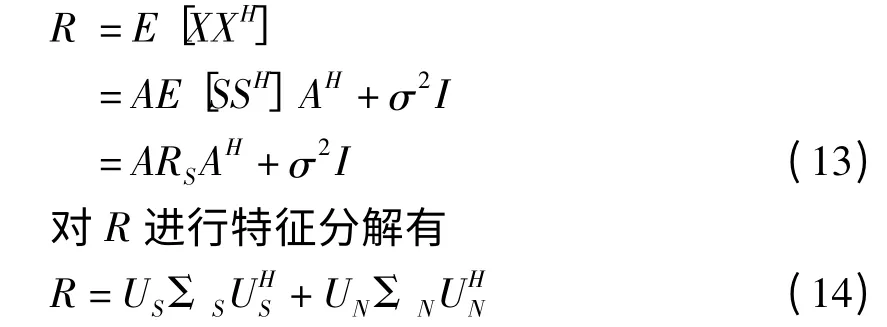
实际接收的数据矩阵是有限长的，其协方差矩阵的最大拟然估计为

式中，L—快拍数。对R^进行特征分解可以计算得到噪声子空间特征矢量矩阵U^N，此时MUSIC 算法的谱估计公式为

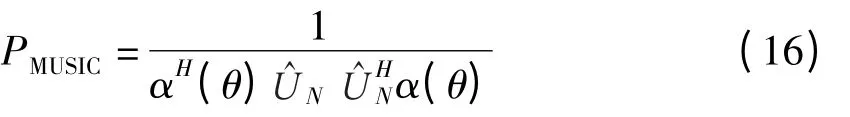
电机故障诊断流程框图如图1 所示

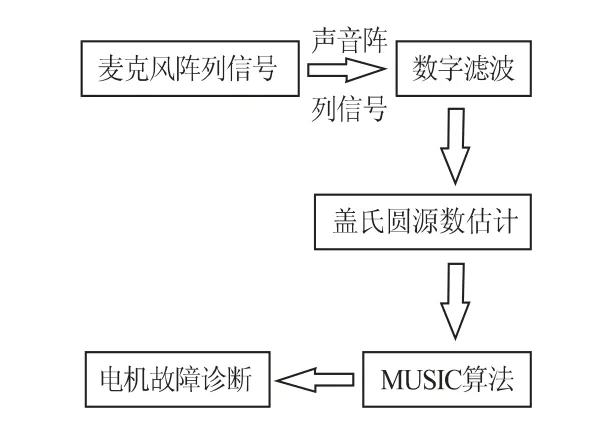
图1 电机故障诊断流程框图

3 实验分析

3.1 故障现象

现有一台YD 型65kW 故障电机，额定转速988r/min，防护等级IP44。其负载为一大型液压油泵。电机起动时，瞬间起动电流达198A，但很快进入空载稳定状态。此时电机噪声较小，一旦加上负载，噪声马上增大，用声压计测得其增幅达到110dB(A)，已经超出电机噪声A 计权声功率级LW限值(98dB(A))。

明显地，电机故障噪声随负载增加而增大，负载与电流密切相关，而电流直接影响电机磁场，故初步估计该噪声为电磁噪声。

3.2 数据分析

在电机运行现场，与电机转子水平方向外1m处以间隔L 为0.16m 放置8 个麦克风(如图2 所示)，形成与转子平衡的直线传感器阵列。

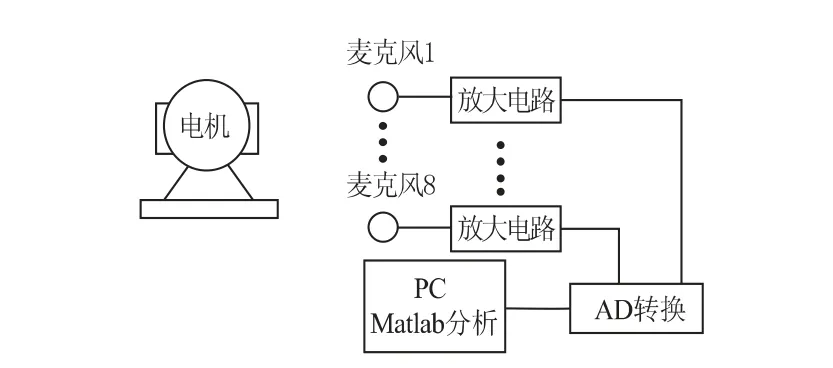
图2 麦克风传感器阵列

整个观测时间为5s，主要采集电机由轻载到重载过程中的声音数据，采样频率为44kHz。图3为其中一个采集电机噪声的麦克风所截取的一部分数据。从图中可以看出负载运行开始至加重负载其噪声值明显增大，这表明电机带载运行时，其内部异常冲击振动明显增强。

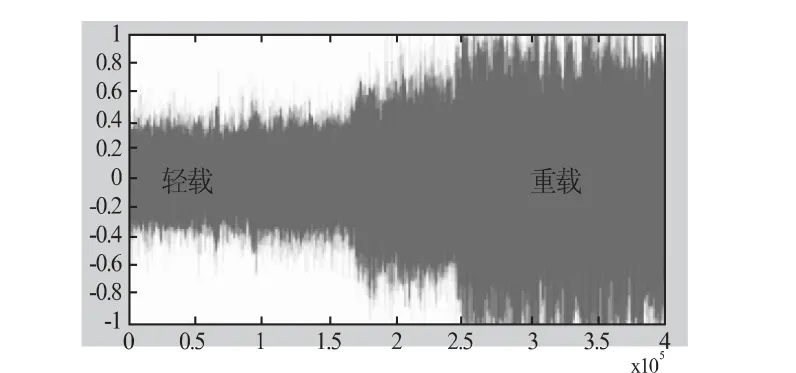
图3 电机噪声数据采集

图4 为电机运行过程中三维瀑布图。从图中可以看出随着负载的增大，电机的故障频率愈加明显，其中出现一个典型的故障频率f=230Hz，该频率还存在二阶、三阶等高阶特征频率分量，其幅值呈下降趋势，而且无调制边带。

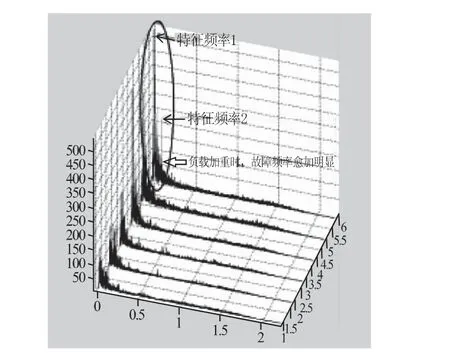
图4 电机运行三维瀑布图

如上所述，盖氏圆算法及MUSIC 算法不适合用在宽带频域上。又从图4 中可以看出，电机的故障频率主要集中在1.5kHz 频率范围内，故可将采集的噪声经数字滤波后进行电机的故障诊断。其巴特沃斯滤波器设计参数为fp=2100，fs=2500，Rp=3dB，Rs=25dB。经滤波后的数据进行盖氏圆算法分析，其源数估计如图5 所示，即有三个主要声源，其MUSIC 谱如图6 所示，即入射方向分别是34.59°、42.02°和67.21°。对应传感器与电机的摆放位置，其指向的位置分别是轴承方向(34.96°，误差1.07%)、电机定子外壳(41.38°，误差1.54%)和电机风扇位置(68.69°，误差2.20%)。

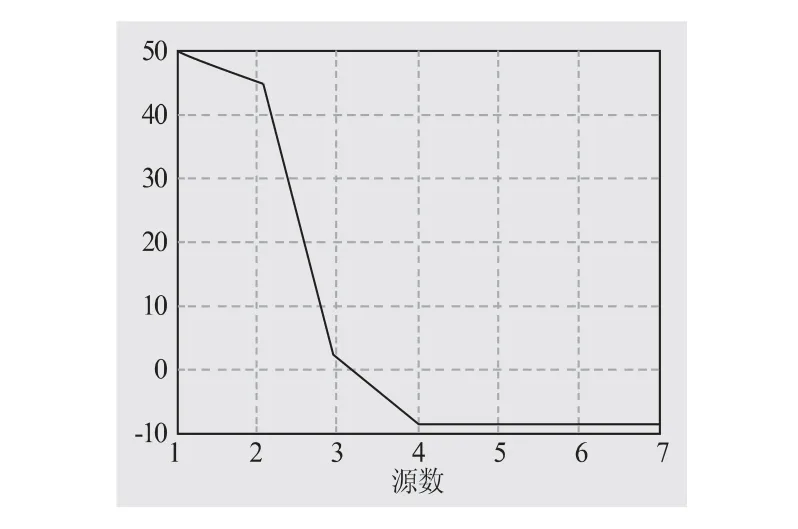
图5 源数估计

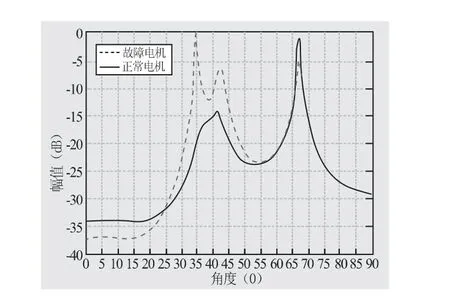
图6 MUSIC 入射谱

3.3 故障诊断

从图6 故障电机与正常电机的MUSIC 谱图中可以看出，其中故障信号的入射源明显。正常电机在运行时，由于没有受到异常冲击碰撞，其整体运动辐射的噪声在电机附近空间范围内声场均匀，而空气动力噪声为此系列电机固有的正常噪声，故结合故障电机所发出的噪声源、方向及故障频率，判断电机的噪声源主要来自以下三个原因。

(1)转子动偏心。从电机运行三维瀑布图中可以看到故障频率f 及其所带无调制边带，其频率为两倍转差频率。正是由于转子不平衡所引发的拍频振动特征，其特征频率是以边带谱反映出来的［7］，这种低频噪声在人耳听起来是一种时高时低的“嗡嗡”声。返修电机的反馈数据，其电机轴垂直气隙相差0.15mm，水平气隙相差0.04mm。

(2)轴承故障。由于转子不平衡使得轴承的保持架和滚动体之间产生摩擦，如果轴承的负载过大会加剧电机发生振动和噪声。

(3)空气动力学噪声。大部分异步电机总会存在一定的风扇噪声，这是由于电机内部空气在固定障碍物上擦过而产生。

综上，经过合理分析后决定重新装配电机转子，同时更换已损坏的轴承，改用某一进口轴承。用声压计重新测试电机从起动、轻载至重载过程，发现电机能正常、平稳工作，经多次检测其噪声值保持在77 ～83dB 左右，其噪声值大大降低，已经符合电机噪声A 计权声功率级LW限值。从结果可以得出利用声音阵列信号及对电机故障信源的估计能正确、有效的解决电机故障问题。