双足机器人NAO爬楼步态规划

赵宸 陈殿生

（北京航空航天大学机械工程及自动化学院, 北京， 100191）

双足机器人NAO爬楼步态规划

赵宸 陈殿生

（北京航空航天大学机械工程及自动化学院, 北京， 100191）

双足机器人的爬楼梯性能是衡量其在复杂环境下行走能力的一项重要指标。本文针对双足机器人NAO爬楼梯步态规划问题，提出一种离线步态规划方法：基于几何法建立机器人爬楼梯逆运动学模型；将运动解耦为前向运动和侧向运动，对于起步、中步和止步三个阶段，采用加速度空间法和几何约束规划法，计算各关节运动轨迹，并基于其逆运动学模型，得到各关节角序列；分别基于NAOSim和NAO进行虚拟样机仿真实验和实物样机验证。实验结果表明，步态规划方法合理有效。

机器人，NAO，楼梯，步态规划

0 引言

双足机器人的研制开始于上世纪60年代末，在五十多年中，双足机器人的研究工作取得了举世瞩目的成绩，也正在深入人类日常生活的各个方面。双足机器人的步态规划不仅需要考虑系统稳定性，有时还需要建立复杂的运动学或动力学模型，给步态规划带来了挑战。

J. Gutmann[1]等基于参考轨迹法和动力学模型法，在高58cm的QRIO上实现了攀爬高3cm台阶的实验。日本Honda公司的K. Hirai[2]等基于动力学模型法和ZMP控制技术，在高130cm的ASIMO上实现了攀爬高10cm楼梯的实验。S. Kim[3]等采用基于HMCD系统的步行数据法进行步态设计，在高150cm的HRP上实现了攀爬高8cm楼梯仿真实验。

机器人的身高与攀爬楼梯的最大高度之比β是衡量机器人爬楼梯性能的一个关键指标。β表示机器人攀爬楼梯的能力，β值越小，机器人爬楼梯性能越好。ASIMO的β值为13，QRIO的β值为19.3，HRP的β值为18.75。目前，双足机器人爬楼梯的β都较大，爬楼梯性能有待提高。

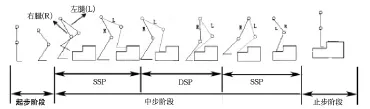
图 1 爬楼梯步态周期的阶段

本文以双足机器人NAO为研究对象，采用加速度空间法和几何约束规划法，求解其关节轨迹，并基于逆运动学模型，求得其全身关节角序列，实现β=11.6的高性能爬楼梯运动。

1 双足机器人爬楼梯的运动学机理分析与建模

1.1 双足机器人爬楼梯的运动学机理分析

一般来说，每个步态周期可分为2个相期（单脚摆动相SSP和双脚支撑相DSP）、3个阶段（起步阶段、中步阶段、止步阶段），如图 1所示。在一个步行周期运动中，双足机器人双腿作为支撑腿运动的时期，称为双脚支撑相(DSP: Double support phase)；双足机器人某只腿作为摆动腿运动的时期，称为单脚摆动相(SSP: Single support phase)。根据对人类爬楼梯行为的观测[4]，双脚支撑相比一般大于等于10%。

1.2 双足机器人的逆运动学建模

由于逆运动学存在解的存在性和唯一性问题，本文选择踝关节和机器人质心作为已知的关节坐标，利用几何法进行逆运动学求解。下面分别对于双足机器人的摆动腿和支撑腿，建立几何模型，如图 2和图 3所示。图中，L1为机器人小腿长度，L2为机器人大腿长度，L3为支撑腿的踝关节中心点A1到同侧的髋关节中心点C1的距离，L4为摆动腿的踝关节中心点A2到同侧的髋关节中心点C2的距离，ZCH是机器人质心PCOM和两髋连线中点D沿Z轴的距离，XCOM和ZCOM是机器人质心在矢状面XOZ中的坐标，XANKLE和ZANKLE是机器人摆动腿的踝关节中心点A2在矢状面XOZ中的坐标。

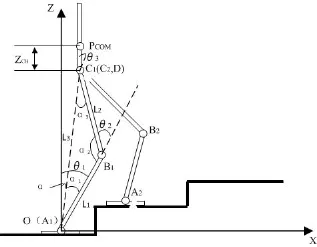
图 2 几何法逆运动学求解(支撑腿)

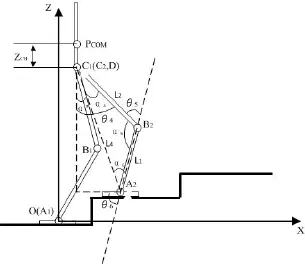
图 3 几何法逆运动学求解(摆动腿)

1.2.1 支撑腿的逆运动学求解

根据图 2中的几何关系，可知支撑腿的踝关节中心点A1到同侧的髋关节中心点C1的距离L3和A1C1与Z轴的夹角α为

由式(1)和式(2)可知，支撑腿的关节角序列为

1.2.2 摆动腿的逆运动学求解

根据图 3中几何关系可知，

由式(4)和式(5)可知，摆动腿的关节角序列为

2 人形机器人爬楼梯的步态规划

2.1 双足机器人爬楼梯的起步和止步步态设计

2.1.1 起步和止步运动轨迹规划

由于在起步阶段的运动处于准静平衡态，导致起步阶段无法直接应用倒立摆模型，因此采用加速度空间规划方法[5]。为了降低机器人从静止加速到步行速度的能耗，同时便于由起步阶段更快地过渡到单脚支撑相，采用降低机器人重心的方法，将机器人的势能转换为动能，有：

由式(7)以及NAO的技术说明书[6]，计算可得完成起步步态后，点PCOM与地面高度差为195mm，如图 4所示。为保证运动的平滑性，采用正弦函数作为起步运动轨迹函数，XCOM(t)和ZCOM(t)表示质心沿X轴和Z轴的运动轨迹，本文设定起步运动时间t=2s，则有

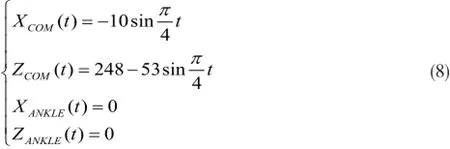
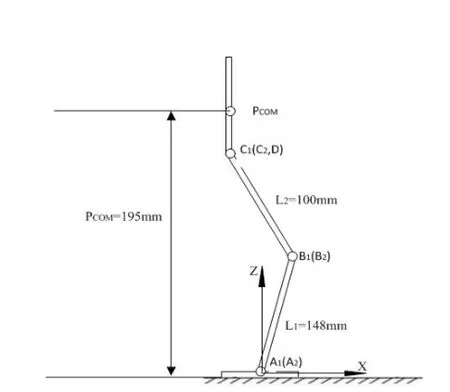
图 4 起步阶段的最终姿态

止步步态规划是起步步态规划的逆过程，同样采用加速度空间规划法，初始姿态即为起步步态规划的最终姿态最终姿态即为机器人双脚并齐的零位移、零速度的初始站立状态。因此，采用正弦函数作为止步运动轨迹函数，即

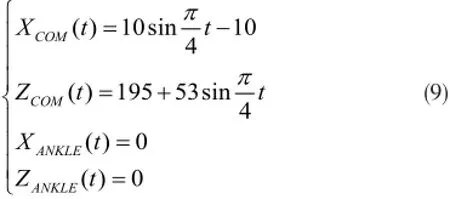
2.1.2 起步和止步运动关节角序列求解

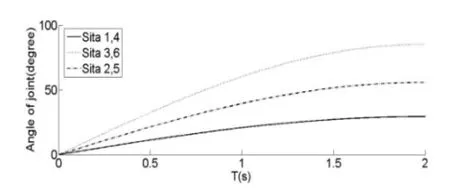
图 5 起步阶段关节角序列

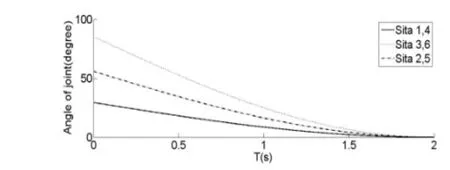
图 6 止步阶段关节角序列

2.2 双足机器人爬楼梯的中步步态规划

2.2.1 前向运动轨迹规划

中步运动轨迹规划是机器人爬楼梯动态步态规划的核心问题。在一个步行周期内，分别对其质心和摆动腿踝关节进行运动轨迹规划。

1) 质心运动轨迹规划

由于机器人爬楼梯时质心随着楼梯高度不断变化，因此采用一阶变杆长倒立摆模型对质心运动轨迹进行规划。以机器人质心PCOM到摆动腿踝关节中心点距离l(t )为摆长，机器人摆动腿踝关节中心点为摆点，假设支撑腿和摆动腿与台阶的接触点处于台阶中心位置，且中步阶段初始和终止时刻机器人质心PCOM在台阶竖直边界的延长线上，建立的模型如图 7所示。

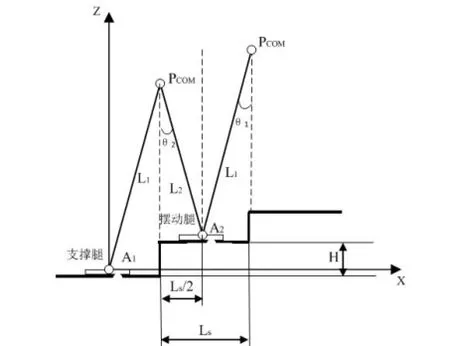
图 7 机器人前向变长倒立摆模型

在图 7中，Ls为机器人单步步长或楼梯深度，H为楼梯高度，L1是中步阶段初始时刻机器人质心PCOM到支撑腿踝关节中心点距离，L2是中步阶段最终时刻机器人质心PCOM到摆动腿踝关节中心点距离。

根据图 7中的几何关系，L1和L2的关系为

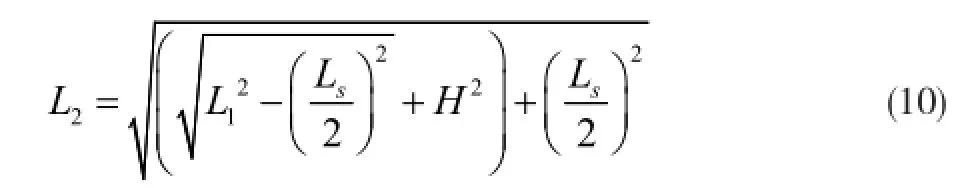
设θ()t 为质心与摆动腿踝关节中心点连线与Z轴的夹角，即变长倒立摆的摆角，则根据一阶倒立摆运动方程，有

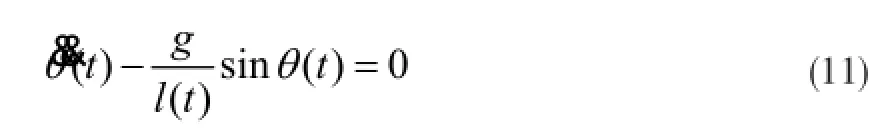
为简化计算，令l(tl=l1，则此二阶微分方程的通解为

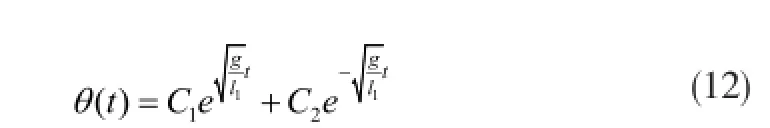
下面推导此微分方程的两个边界条件。

在初始时刻t=0时，有

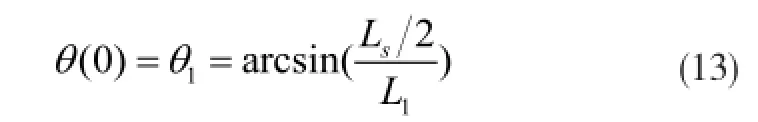
在终止时刻t=T时，有

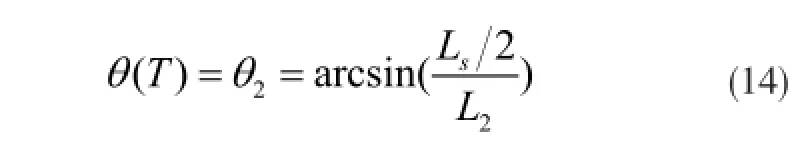
由式(12)、式(13)和式(14)可知，变长一阶倒立摆的摆角θ()t 为

假设倒立摆的杆长变化率为常数，则变长一阶倒立摆的摆长() lt 为

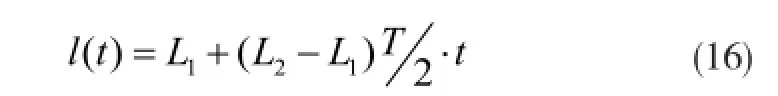
由式(15) 和式(16) 可知，机器人前向质心轨迹为

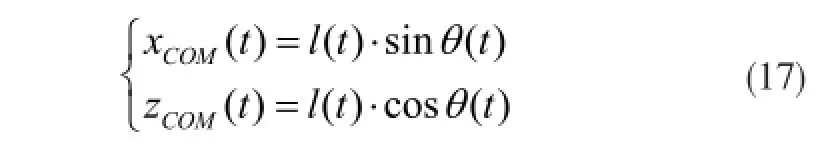
2) 摆动腿的踝关节运动规划为避免爬楼梯过程中机器人与外部环境发生碰撞，本文采用几何约束法对摆动腿踝关节沿X轴和Z 轴的运动轨迹进行规划，其几何约束如图 8所示。

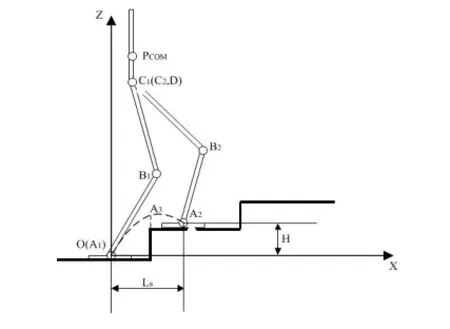
图 8 双足机器人爬楼梯的踝关节几何约束

根据图 8所示的几何关系，在一个步行周期内，沿X轴摆动腿由0移动到LS。同时，为保证运动的稳定性和平滑性，假设在起始时刻t=0和终止时刻t=T沿X方向位移的一阶导数为0，双足机器人的初始位置保证其在爬楼梯过程中不会与外部环境在X轴方向发生碰撞。本文采用三次样条插值函数对摆动腿踝关节沿X轴的运动轨迹() ANKLE Xt 进行规划，其数据表如表 1所示。

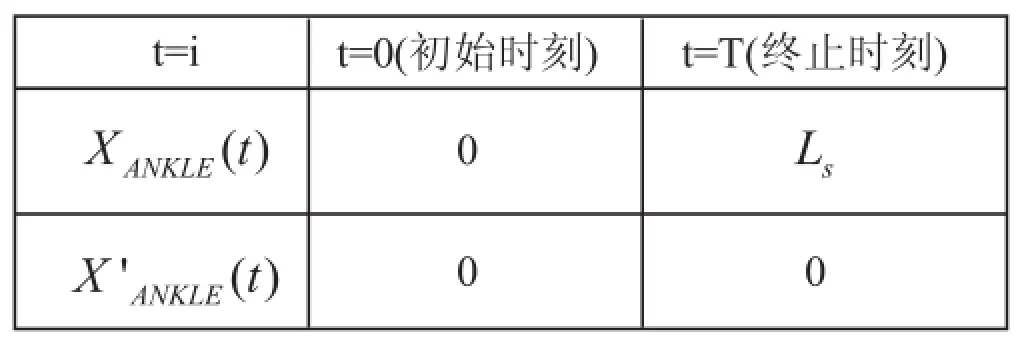
表 1：()ANKLEXt 插值函数数据表

可求得三次样条插值函数为：

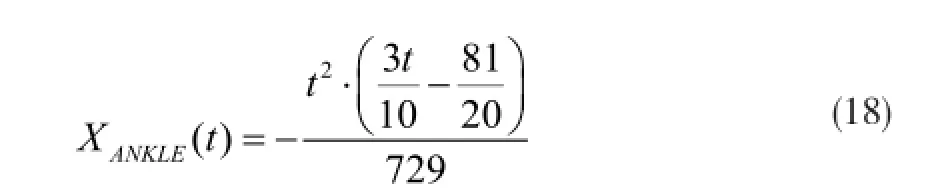
为了避免摆动腿与外部环境的碰撞，机器人的摆动腿在A3处(t=t3)沿Z轴的坐标应大于H，这里假设其沿Z轴坐标为H+0.1，并假设摆动腿在中间时刻()达到最高点Hmax，采用三次样条插值函数规划摆动腿踝关节的运动轨迹，其数据如表 2所示。

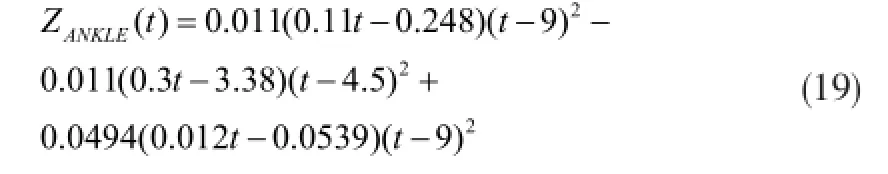
可求得三次样条插值函数为：表 2：() ANKLE Zt 插值函数数据表

2.2.2 侧向运动轨迹规划

机器人在爬楼梯过程中，于起步和止步阶段，其质心和踝关节在冠状面上无运动轨迹，因此，这里只需要对中步阶段质心进行侧向运动轨迹规划，采用定长一阶倒立摆模型对其进行运动轨迹规划。

以机器人支撑腿踝关节中心点A1为摆点，机器人质心PCOM到支撑腿踝关节中心点A1的距离L5为摆长，摆角为θ'(t)，建立如图 9所示的一阶倒立摆模型。

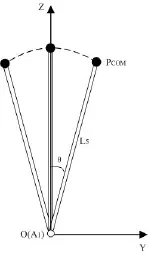
图 9 侧向质心轨迹规划的一阶倒立摆模型

根据一阶倒立摆方程(11)可知

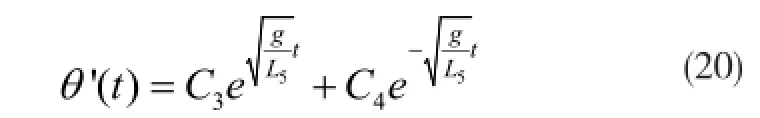
微分方程(11)的边界条件为

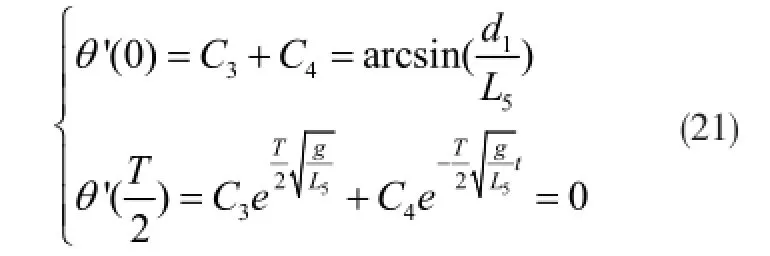
由式(20)和式(21)可知，

因此，质心侧向运动轨迹沿Y轴和Z轴的位移为

机器人正向的七杆模型如图 10所示，图中，θ7～θ12为腿部关节角序列。由于将侧向运动视为定长的倒立摆模型，因此有θ7=θ8=…=θ12。

下面推导摆角 与θ9之间的关系。

由图 10的几何关系可知，

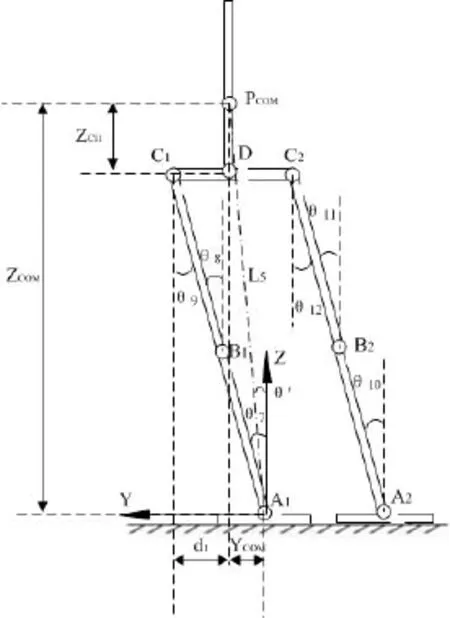
图 10 机器人七杆模型(正视图)

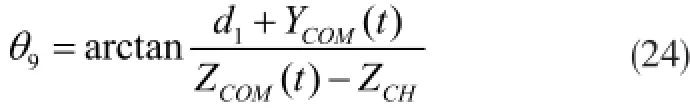
2.3 中步阶段关节角序列求解

根据逆运动学模型，可得中步阶段前向关节角序列{θi}(i=1,2,…,6)如图 11所示，侧向关节角序列{θi} (i=7,8,…,12)如图 12所示。

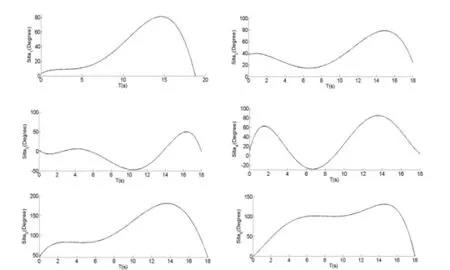
图 11 前向关节角序列

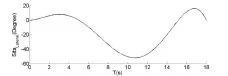
图 12 侧向关节角序列

3 基于NAOSim的仿真试验

NAOSim是用于在三维虚拟现实环境中测试NAO的行为和算法。在NAOSim中导入机器人全身关节角序列，仿真结果如图13和表 3所示。

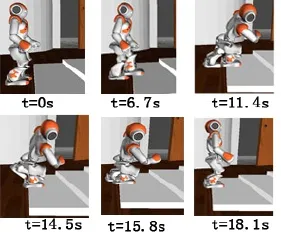
图13 基于NAOSim的机器人爬楼梯仿真试验

表 3：仿真试验的技术指标

4 基于NAO的物理样机试验

Choregraphe是一款专用于NAO的用户友好的行为编辑器，可通过不同方式为机器人编程。在Choregraphe中导入机器人全身关节角序列，实验结果如图14和表4所示，实验结果表明，NAO能够攀爬5.2cm的台阶。

图14 NAO爬楼梯的物理样机试验

表 4：物理样机试验的技术指标

5 结论

本文根据双足机器人爬楼梯的运动机理，基于几何法推导了双足机器人爬楼梯的逆运动学模型。同时，将爬楼梯的过程分为起步、中步、止步三个阶段，在起、止步阶段和中步阶段分别采用加速度空间规划法和几何约束法进行运动轨迹规划，并基于逆运动学模型，求解机器人爬楼梯过程中全身关节角序列。在仿真环境NAOSim与物理样机NAO上，分别进行了攀爬高度为5cm的楼梯试验，试验结果表明，本文所采用的离线步态规划方法合理、可行。

[1] Gutmann J,Fukuchi M, et al. Stair Climbing for Humanoid Robots Using Stereo Vision[C]. Intelligent Robots and Systems IEEE/RSJ International Conference,2004(2)： 1407-1413

[2] Hirai K,Hirose M, Haikawa Y , Takenaka T. The development of Honda humanoid robot. IEEE Int. Conf. Robotics and Automation. Leuven. Belgium, 1998： 1321-1326.

[3] Kim S, Sankai Y. Stair Climbing Task of Humanoid Robot by Phase Composition and Phase Sequence[C]. IEEE International Workshop on Robots and Human Interactive Communication, 2005：531-536

[4] Chen C T. Linear system theory and design [M]. 3rd edition.New York： Oxford Press, 1999： 25

[5] 柯显信. 仿双足机器人双足动态步行研究[D]. 上海：上海大学. 2005 ：63-65

[6] Aldebaran Robotics. NAO Software documentation[EB/OL]. http：//www.aldebaran-robotics.com/documentation/family/nao_h25/links_h25.html.