基于离散元的多分辨率信号去噪新方法
2013-03-03张江源林福泳
张江源,林福泳
(华侨大学 机电及自动化学院,福建 厦门361021)
实际工况中得到的信号大都是含噪信号,受噪声影响,直接对采集信号进行分析处理是不精确的,为了对信号进行较准确分析,需要将有效信号从含噪信号中提取出来,从而达到信号去噪的目的[1].多分辨率分析是小波分析的重要内容,是目前小波分析的重要应用之一.它之所以重要在于它可以多层次地分解描述信号,并能由细到粗地分析信号,便于提取信号的细微特征,从而检测出突变信号[2-3].多分辨率分析能够有效地提取信号的稳态及瞬态信息和波形特征,有效地区分信号中的突变部分和噪声部分,因此适用于信号处理[4].小波信号去噪方法大体上可分为3种:1)Mallat等[5]提出的基于小波变换的模极大值去噪方法;2)Donoho[6]提出的基于小波阈值滤波的去噪方法;3)对含噪信号进行小波变换后,计算相邻尺度间小波系数的相关性,并根据相关性分析不同的小波系数,从而进行取舍,然后直接重构信号[7-8].本文提出一种基于离散基的多分辨率信号去噪新方法,对噪声信号进行去噪处理.
1 离散基的定义

2 基于多分辨率分析的信号去噪
2.1 多分辨率分析
设信号数据为a0,a1,…,an-1,将信号扩为2n-2的周期信号,即有

应用离散基将f(x)分解为基本信号f1(x)和误差信号e1(x),得
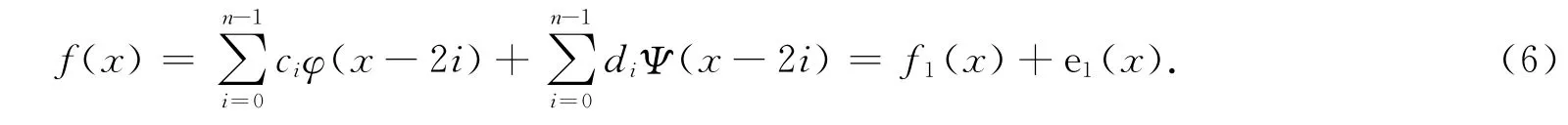
将式(6)的两边乘以Ψ(x-2i)并对各点求和,结合式(3),可得

用循环矩阵求逆矩阵的方法[9],可以得到递推公式,进而求得di,最后得到误差为

将信号f(x)减去误差信号,即得到基本信号:a′0,a′1,…,a′2n-2.

多分辨率重构算法是其分解算法的逆过程,其数据重构过程为

2.2 阀值法去噪
若要从含噪信号中去除噪声信号,可分为3个步骤.
1)信号分解.设噪声信号为f(t),s(t)是纯净信号,n(t)为高斯白噪声,则有

将噪声信号f(t)进行多分辨率分解至确定层数,得到相应的误差系数ej,k.


3)信号重构.将经过阈值处理过的误差系数进行信号重构,得到恢复的原始信号的估计值,即去噪后的信号[10].
3 实验与分析
3.1 不同滤波方法的比较
应用多分辨率信号去噪方法,取适当的离散基系数,对加噪信号进行5层分解,并与Matlab小波工具箱采用最佳系数及分解层数组合的小波基[11]进行比较.其中,SNR为信噪比;MSE为均方误差.haar做3层分解;db做3层分解,消失矩取1;sym做3层分解,消失矩取2.分别对Bumps和Doppler加噪信号(SNR=15 d B)进行去噪处理,并用软阈值法去噪,实验结果如表1所示.
从表1可以看出:用本文方法可以更好地去除噪声,细节损失较少,波形光顺性较好,更逼近原始信号.从表1还可知:本文方法在去噪处理中,可以获得更高的信噪比和更小的均方误差,信噪比和均方误差等性能指标较传统滤波方法均有明显提高.
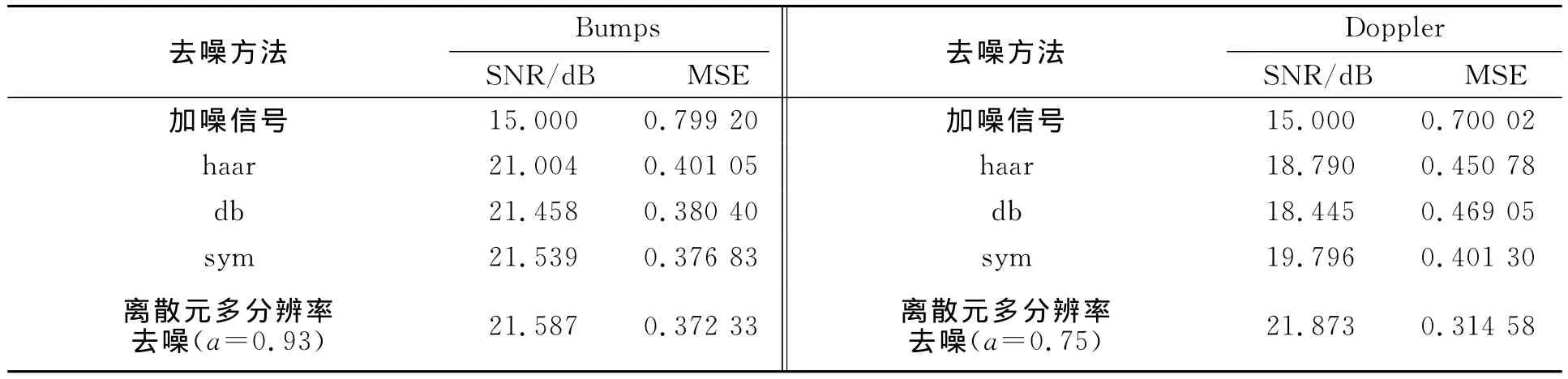
表1 对Bumps和Doppler加噪信号滤波后的数据Tab.1 Filtered data of the Bumps and Doppler noise signal
3.2 不同离散基系数的比较
应用离散元多分辨率信号去噪方法,取离散基系数(a)为0.55,0.65,0.75,0.85,0.95,1.05,1.15,分别对Bumps,Doppler加噪信号(SNR=15 dB)进行5层小波分解,并分别用软阈值法、硬阈值法去噪,实验结果如表2所示.
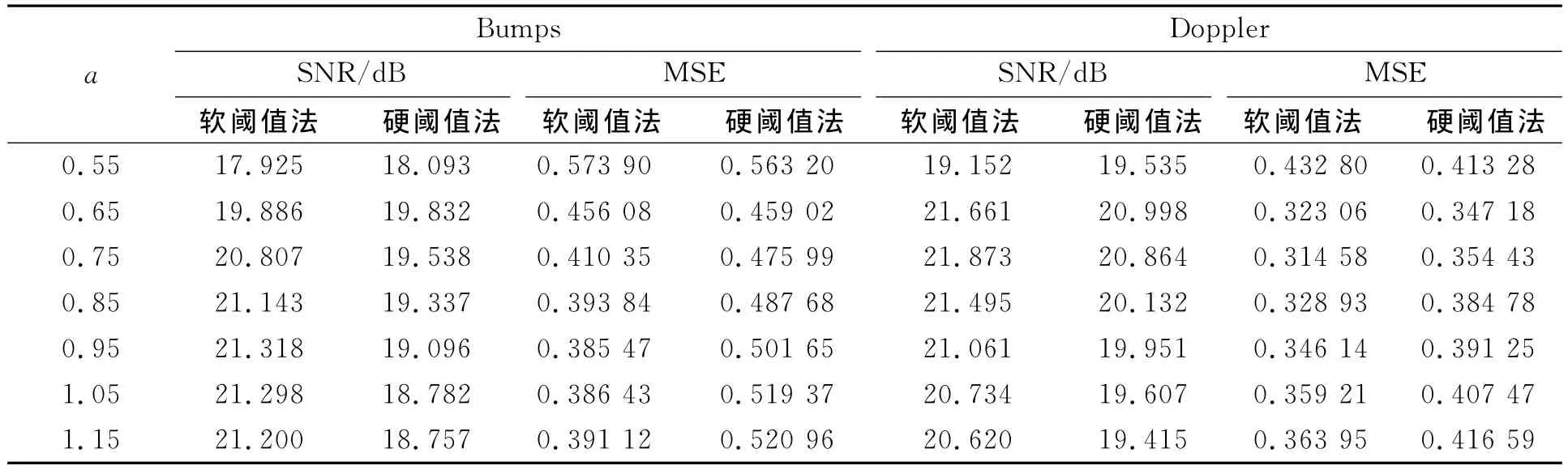
表2 取各离散基系数对Bumps和Doppler加噪信号滤波后的数据Tab.2 Filtered data of the Bumps and Doppler noise signal by each discrete base coefficient
从表2中的数据发现:采用硬阈值法去噪后,信噪比及均方误差较平均,但最佳值不如软阀值法;采用软阈值法去噪后,信噪比及均方误差波动较大,但最佳值优于硬阈值法.比较各离散基系数的去噪结果可知,文中方法的离散基系数在0.75附近达到较好的信噪比及均方误差等性能指标.
4 结论
本文提出一种信号去噪方法,其基本原理基于最小二乘法.所提出的离散基具有显式表示,可以按照实际需要,改变离散基,因此方便于应用.通过对加噪信号进行去噪处理,实验表明:该方法可以有效地保留信号中更多的有效成分,信噪比和均方误差等性能指标较传统滤波方法均有明显提高,是一种有效的信号去噪新方法.
[1] 张明,李开成,胡益胜.基于小波邻域阈值分类的电能质量信号去噪算法[J].电力系统自动化,2010,34(10):84-89.
[2] 林福泳,王太勇.一种信号多辨分析的新方法[J].西南交通大学学报,2003,38(5):574-577.
[3] 林福泳.正交样条的多分辨分析方法[J].华侨大学学报:自然科学版,2005,26(2):180-183.
[4] 王睿,山拜·达拉拜.一种新阈值函数的小波信号去噪研究[J].通信技术,2011,44(1):50-52.
[5] MALLAT S,HWANG W L.Singularity detection and processing with wavelets[J].IEEE Transactions on Information Theory,1992,38(2):617-643.
[6] DONOHO D L.De-noising by soft thresholding[J].IEEE Transactions on Information Theory,1995,41(3):613-627.
[7] DAUBECHIES I.The wavelet transform,time frequency localization and signal analysis[J].IEEE Transactions on Information Theory,1990,36(5):961-1005.
[8] DONOHO D L,JOHNSTONE I M.Ideal spatial adtation via wavelet shrinkage[J].Biometrika,1994,81(1):425-455.
[9] LIN Fu-yong.The inverse of circulant matrix[J].Applied Mathematics and Computation,2011,217(21):8495-8503.
[10] BRUCE A G,GAO Hong-ye.Understanding wave shrink:Variance and bias estimation[J].Biaretrika,1996,83(4):727-745.
[11] 张恒,李安宗,屈景辉.无线随钻测量系统信号处理的小波基选取[J].测井技术,2007,31(3):285-288.
