基于区间模糊数的模糊线性回归模型及其应用

付云鹏，郭云峰，马树才

(1辽宁大学信息学院，辽宁沈阳，110036;2沈阳大学经济学院;3辽宁大学经济学院)

线性回归模型是统计推理中一类应用较为广泛的模型，在工程技术、社会经济等各个领域都有着广泛的应用。但是经典的线性回归模型只能讨论精确数据，当数据稀少、无统计意义、数据的信息具有不确定性时，经典的线性回归模型无法解决这类问题。模糊集理论的提出为解决这类问题奠定了理论基础。1982年，H.Tanaka等［1］首次提出了模糊线性回归模型;胡良剑等［2］研究了对称三角模糊数据的线性回归模型;王丽军等［3］采用梯形模糊数讨论了一元模糊线性回归模型;谷振涛等［4］运用模糊线性规划模型对井群系统开采量总和进行了测算。宋业新等［5］讨论了具有模糊不等式约束和模糊等式约束的模糊系数线性规划问题的求解方法，将转化为区间数规划问题求解。赵海坤等［6］提出目标函数和约束条件中均含有模糊数的模糊线性规划问题，利用模糊数的排序关系将其转化为经典线性规划的方法求解。高淑萍等［7］利用一种新的模糊数排序关系解决了含有三角模糊数的模糊线性规划问题，并将其应用于具有模糊等式约束的运输问题。笔者将以区间模糊数为研究对象建立模糊线性回归模型，并给出最小二乘意义下的参数估计方法，最后结合沈阳市的温度变化情况给出该模型的实际应用。

1 预备知识

定义1［8］实数域R到区间［0，1］的映射称为R上的模糊数，如果满足:

(1){x|(x)≥α}为闭区间，(α∈(0，1));(2)存在x0∈R使(x0)=1。

定理1［9］(区间模糊数的运算规则)设［a，b］，［c，d］是区间模糊数，则由扩展原理可得以下结论:

(1)加法 ［a，b］+［c，d］=［a+c，b+d］

(2)减法 ［a，b］－［c，d］=［a－d，b－c］

(3)乘法 ［a，b］×［c，d］=［min{ac，bc，ad，bd}，max{ac，bc，ad，bd}］，特别地，当a＞0，c＞0 时，有［a，b］×［c，d］=［ac，bd］

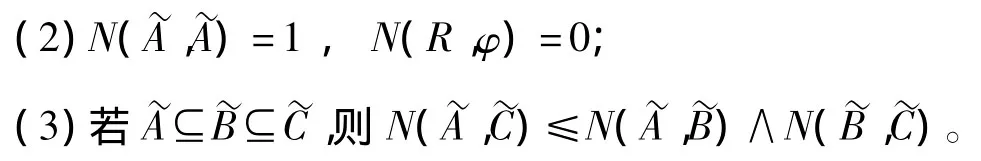
则称N(，)为模糊集与的贴近度，称N为F(R)上的贴近度函数。

贴近度是对两个模糊集之间接近程度的一种度量，是一个原则性的概念。其具体规则可视实际需要而定，在此只介绍一种测度贴近度［8］。

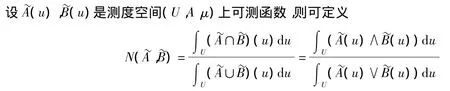
上述积分为勒贝格积分，若U为实数域R，被积函数为黎曼可积，且广义积分收敛，则上述积分化为

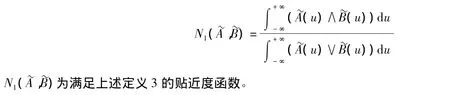
设［a，b］，［c，d］是区间模糊数，则两个模糊数［a，b］，［c，d］之间的贴近度为N(［a，b］，［c，d］)为

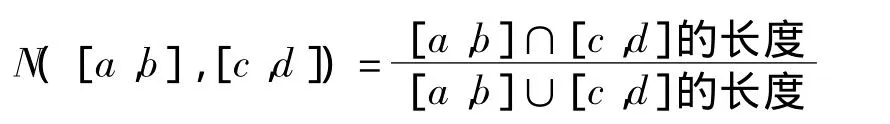
贴近度刻画了［a，b］，［c，d］之间的接近程度，贴近度越大，则两个模糊数越接近，这等价与计算d2(［a，b］，［c，d］)=(c－a)2+(d－b)2，d2越小，则两个区间模糊数之间的贴近度越大，两个模糊区间数越接近，于是给出如下定义:

定义4 设［a，b］，［c，d］是区间模糊数，则为区间模糊数［a，b］，［c，d］之间的距离。

事实上，定义4中的距离定义满足距离的3条公理。

设［a，b］，［c，d］，［e，f］为3 个任意的区间模糊数，则

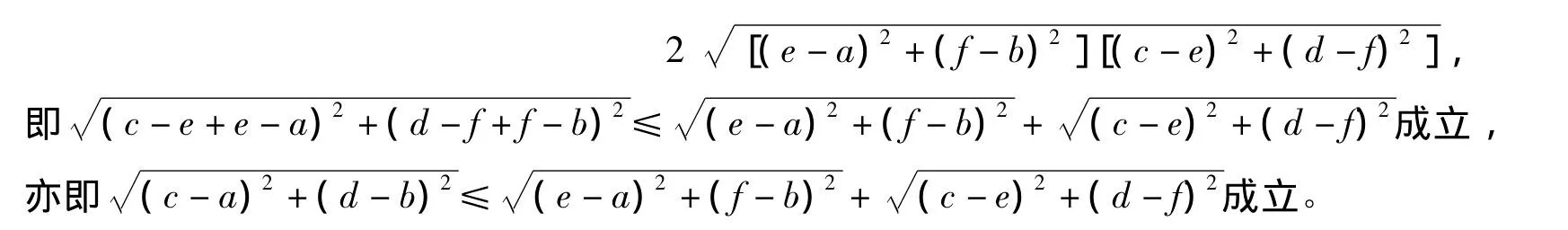
综上所述，定义4中的距离满足3条公理，因此是一种合理的距离定义。

2 多元模糊线性回归模型

2.1 自变量为实数，因变量和参数为区间模糊数的模糊线性回归模型

2.2 自变量和因变量均为区间模糊数，回归系数为实数的模糊线性回归模型

2.3 自变量、因变量和回归系数均为区间模糊数的模糊线性回归模型

3 模型的应用

沈阳市1995～2011年的全年最低气温和最高气温数据如表1所示，数据具有区间模糊数的特点。为研究该城市的温度随时间的变化情况，可建立含有区间模糊数的模糊线性回归模型。其中自变量xi为实数，因变量为区间模糊数立如下模型

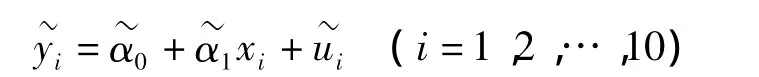
将样本数据代入到模型中，按照模型(2)的估计方法求出各参数的估计值为

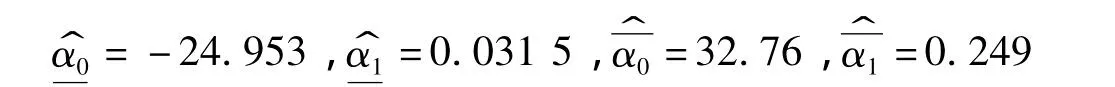
于是可得模糊线性回归的估计模型为

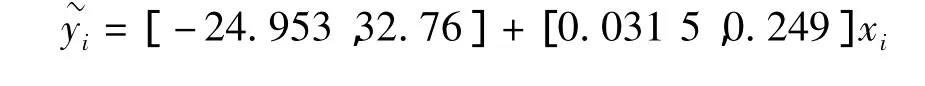
当xi=11时，求得=［－24.606 7，35.500 0］，即为2011年沈阳市气温的预测值，其真实值为［－23.8，32.3］，真实值与预测值之间的贴近度为0.933 34，说明应用该模型进行预测的预测效果较好。

表1 沈阳市2001～2011年的全年最低气温和最高气温数据

4 结 论

笔者提出含有区间模糊数的线性规划问题，并就不同的系数类型分别讨论了模型的求解方法，给出不同模型的参数估计方法，最后结合沈阳市温度预测问题给出模型的实际应用。实证结果表明:该模型的预测精度较高，对2011年沈阳市的最高温度和最低温度作为区间模糊数进行预测时，预测值与实际值的贴近度达到了0.933 34，说明该模型有一定的实际应用价值。

［1］ TANAKA H，UEJIMA S，ASAI K.Linear Regression Analysis with Fuzzy Model［J］.IEEE Trans System Man Cybernet，1982，12:213-222.

［2］ 胡良剑，宗云南.模糊数据的线性回归模型［J］.模糊系统与数学，2002，16(1):87-95.

［3］ 王丽军，冯玉瑚.模糊线性回归模型的参数估计［J］.东华大学学报:自然科学版，2006，32(6):38-42.

［4］ 谷振涛，潘俊.用模糊线性规划计算井群开采量［J］.沈阳大学学报:自然科学版，1996(2):16-23.

［5］ 宋业新，姜礼平，陈绵云.一类模糊线性规划模型的模糊最优区间值［J］.模糊系统与数学，2002，16(2):86-91.

［6］ 赵海坤，郭嗣琮.一类全系数模糊线性规划的求解方法［J］.模糊系统与数学，2009，23(3):139-144.

［7］ 高淑萍，刘三阳.一类模糊线性规划的求解方法及应用［J］.系统工程与电子技术，2005，27(8):1 412-1 415.

［8］ 胡宝清.模糊理论基础［M］.武汉:武汉大学出版社，2006.

［9］ 杨纶标，高英仪.模糊数学原理及应用［M］.广州:华南理工大学出版社，2002.

(责任编辑:朱宝昌)