3.0T磁共振相控阵线圈信噪比计算方法的定量对比研究

【作 者】王龙辰，金玮，李逸明，李斌

上海交通大学附属第六人民医院 医学装备处，上海市，200233

3.0T磁共振相控阵线圈信噪比计算方法的定量对比研究

【作 者】王龙辰，金玮，李逸明，李斌

上海交通大学附属第六人民医院 医学装备处，上海市，200233

采用对ACR单幅图像法和NEMA两幅图像法两种相控阵线圈进行信噪比测量，计算得到两种方法的相关性方程，并对两种方法进行相互可替代性分析。结果表明两者在评价线圈性能上具有可替代性，但由于消除了系统的结构噪声，使NEMA两幅图像法的测量结果高于ACR单幅图像法。

信噪比； 相控阵； 射频线圈

0 引言

近年来，磁共振射频线圈技术的发展非常迅速，线圈的形状、种类呈现多样化，而其中相控阵线圈是目前应用最广泛的一种射频线圈[1-2]。射频线圈是磁共振设备的重要组成部分，其性能很大程度上决定了成像效果，并最终影响临床诊断，因而对它进行性能评价显得尤为重要[3]。

信噪比是评价磁共振射频线圈性能的重要指标之一，但线圈信噪比的计算方法却多种多样，得到的计算结果也不尽相同[4-6]。线圈结构、系统磁场、结构噪声等都对信噪比有直接影响。相控阵线圈是通过将一系列小的表面线圈单元进行合理组合，使在获得高信噪比的同时又能保证较大的灵敏度范围。但目前并没有对该类线圈不同信噪比计算方法进行过定量研究，因而对相控阵线圈信噪比计算方法进行定量计算研究具有很大的应用价值和实际意义。本文分别采用ACR单幅图像法和NEMA两幅图像法对相控阵线圈进行定量对比研究，得到两种计算方法的相关性方程，并对两者进行可替代性分析。

1 设备和材料

磁共振设备为3.0T Intera Achiva（Philips Medical System，Best，Netherlands），线圈一为8通道相控阵头线圈，线圈二为16通道头颈联合线圈，体模采用的Philips标配的3 000 ml矿物油模。线圈一扫描采用T1W-SE序列，重复时间TR=450 ms，回波时间TE=10 ms，成像视野为FOV=230 mm×183 mm，层厚=4 mm，层数=24，成像矩阵=512×512，采集次数NSA=1。线圈二扫描采用T1W-SE序列，重复时间TR=590 ms，回波时间TE=10 ms，成像视野为FOV=230 mm×183 mm，层厚=4 mm，层数=24，成像矩阵=512×512，采集次数NSA=1。

2 信噪比计算方法

2.1 ACR单幅图像法

ACR（American College of Radiology）单幅图像法是由美国放射协会提出[7]，测量感兴趣区域的平均信号强度作为信号，取背景信号区域的信号标准差作为噪声。信噪比计算公式为：

上式中，S 是ROI区域中的平均信号强度，SDair为视野边角上的空气部分的信号标准差。ROI一般选为圆型，半径为体模面积的90%左右；空气区域则一般较小，位置在FOV的四个角上，占体模半径的10%左右[8]。同时，在空气区域中要避免有明显的伪影和滤波伪影，因为这会导致信噪比计算的明显偏差[9]。

图1 ACR单幅图像法测量信噪比Fig.1 SNR measurement using ACR single image method

2.2 NEMA两幅图像法

NEMA（National Electrical Manufactures Association）两幅图像测量法是利用同样的扫描序列对同一部分连续成两次像，第一次扫描结束到第二次扫描开始的时间间隔不大于5 min[10]，然后将两幅图像相减得到相减后的图像。在相减后的图像的感兴趣区域计算图像的信号标准差作为噪声值，在相减之前的任一幅图像的感兴趣区域中计算图像的信号平均值作为信号值。信噪比计算公式为：

其中，公式中的S表示两幅图像中任一幅图像ROI区域的平均信号强度，SD1-2表示两幅图像相减得到的图像在ROI区域中的信号标准差。由于理想图像的噪声为高斯分布，相减后图像的噪声为原始图像√2倍，因此上式用√2作为信噪比补偿。ROI的选取与单幅图像测量法相同。

图2 NEMA两幅图像法测量信噪比Fig.2 SNR measurement using NEMA dual-image method

2.3 不同方法的对比研究

采用上述两种线圈和序列分别进行了10次成像实验，其中每次实验需运用同一序列参数连续进行两次扫描，用两幅图像法进行图像相减计算线圈信噪比。单幅图像法计算信噪比采用的图像为第一次扫描时产生的图像。用两幅图像法计算信噪比时，采用的图像保证其在两次采集中的层数一致。

关于采用两幅图像计算信噪比，本研究采用MATLAB实现图像的相减运算。为了保证图像信息的完整性，本研究对DICOM图像进行了直接读取并计算，部分程序代码如下所示：

info1=dicominfo(‘IM10-3’. dcm)；

X=dicomread(info1)；f

i gure, imshow(X)；

imcontrast；

imview(X)；

imcontrast；

为了比较两种方法的差异性，我们采用了Bland和Altman提出的统计学方法，对两种不同方法的相关性及可替代性进行了统计分析[11]。该方法是绘制上述两种不同方法得到结果的差值与平均值的坐标图，若数据点在d-2SD和d+2SD（d 表示信噪比差值均值，SD为方差）之间的数目占所有数据的95%以上，则可认为两种方法在评价该指标上是具有可替代性的。

3 结果分析

3.1 测试结果对比

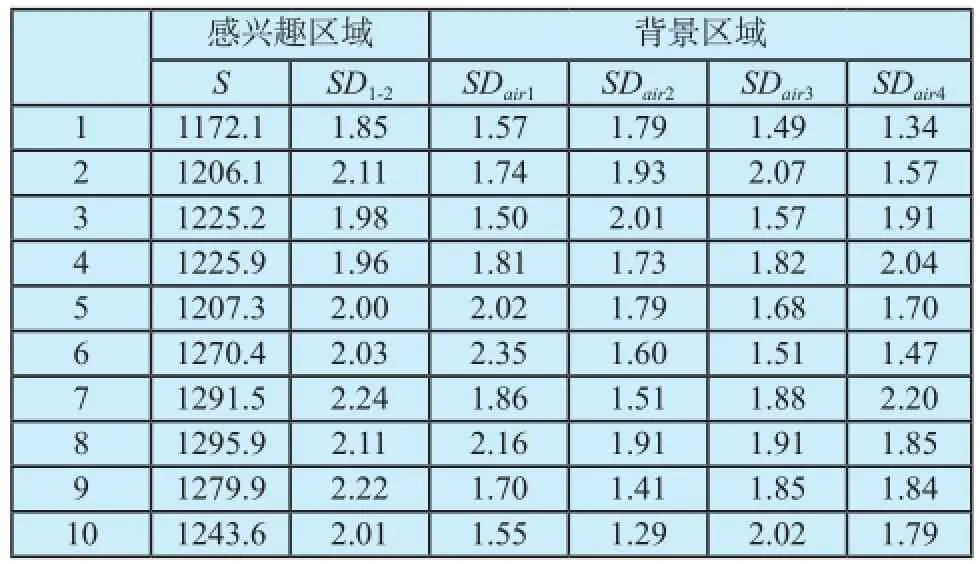
表1 线圈一信噪比测试数据Tab.1 SNR measurement using coil 1

表2 线圈二信噪比测试数据Tab.2 SNR measurement using coil 2

采用8通道相控阵头线圈得到的两种方法测试信噪比的数据如表1所示，采用16通道头颈联合线圈得到得两种方法测试信噪比的数据如表2所示。其中，S为感兴趣区域的平均信号强度，SD1-2为相减后的图像在感兴趣区域的信号标准差，SDair为单幅图像法中air区域的信号标准差。

按照上述两种方法分别计算得到的两种线圈信噪比如表3所示。根据计算结果可以看出，两幅图像法测得的信噪比值都明显高于ACR单幅图像法测得的信噪比值。对于线圈一，ACR单幅图像法10次测得的信噪比的平均值为461.29，两幅图像法10次测得的信噪比的平均值为857.12，两幅图像法测得的信噪比值是ACR单幅图像法测得的信噪比值的1.86倍。对于线圈二，ACR单幅图像法10次测得的信噪比的平均值为637.37，两幅图像法10次测得的信噪比的平均值为1085.30，两幅图像法测得的信噪比值是ACR单幅图像法测得的信噪比值的1.70倍。

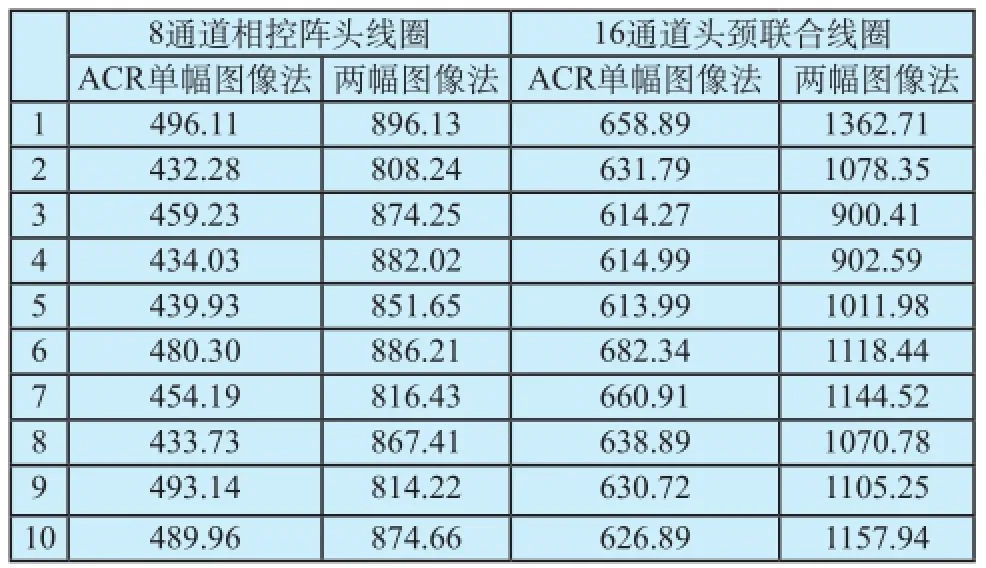
表3 两种线圈不同信噪比计算方法结果Tab.3 SNR measurement results using two coils

3.2 相关性检验分析

采用8通道相控阵头线圈时，运用ACR单幅图像法测得的10次信噪比的平均值为461.29，方差为26.38，两幅图像法测得的10次信噪比的平均值为857.12，方差为32.68。假设采用两种方法测量信噪比时的不确定因素是随机的，即不相关的，则两种方法测量信噪比差值的方差应为

为了比较两种方法的差异性，运用上述统计方法，分别绘制了两种方法计算得到的信噪比差值，关于两种方法的信噪比平均值的坐标图，如图3所示。图中直线为信噪比差值的平均值，两条虚线分别为平均线上移2SD（SD即为上述计算得到的方差）和下移2SD个单位。从图中可以看出，所有的数据点都位于两条虚线之间，即两种方法得到的信噪比差值都介于

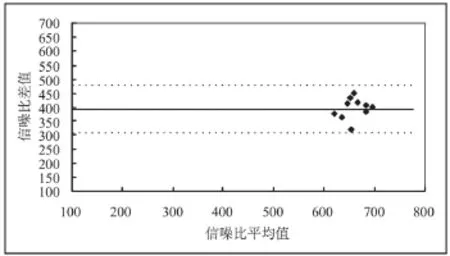
图3 8通道线圈两种方法得到的信噪比差值与均值Fig.3 SNR difference against their mean value between two methods using 8-channel coil

采用16通道头颈联合线圈时，运用ACR单幅图像法测得的10次信噪比的平均值为637.37，方差为23.11，两幅图像法测得的10次信噪比的平均值为108.30，方差为133.52。假设采用两种方法测量信噪比时的不确定因素是随机的，即不相关的，则两种方法测量信噪比差值的方差应为图4为运用16通道头颈联合线圈时两种方法计算得到的信噪比差值关于两种方法的信噪比平均值的坐标图。图中直线为信噪比差值的平均值，两条虚线分别为平均线上移2SD（SD即为上述计算得到的方差）和下移2SD个单位。可以看出，所有的数据点都位于两条虚线之间。

图4 16通道两种方法得到的信噪比差值与均值Fig.4 SNR difference against their mean value between two methods using 16-channel coil

通过上述分析可以看出，采用两种方法计算线圈信噪比时，信噪比差值都位于d-2SD和d+2SD之间。根据统计学原理，当95%的数据点位于(d-1.96SD，d+1.96SD)时，可认为这些数据点为正态分布。因而此处得到的信噪比的差值是服从正态分布的，可以认为两种计算信噪比的方法是可以替代的。

为了更好的描述两种方法的关系，本文对信噪比差值与平均值做了线性回归，如图5所示。图中回归线的斜率为0.5 092，截距为34.776。经过计算得到两种方法信噪比的关系为：

其中SNRsingle为单幅图像法得到的信噪比，SNRdual为两幅图像法得到的信噪比。可以看出，当图像信噪比值较大时，两幅图像法计算得到的信噪比约为单幅图像信噪比的1.68倍。

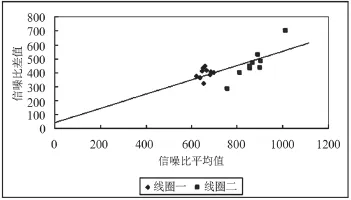
图5 信噪比差值与均值线性回归Fig.5 The regression line of the SNR difference and mean value

4 结论与讨论

通过对单幅图像法与两幅图像法进行细致的比较分析和实验测试对比发现，它们之间存在很好的线性一致关系，两幅图像法得到的信噪比值是单幅图像法测得的信噪比值的1.68倍。通过运用统计方法分析，两种方法计算得到的信噪比差值符合正态分布，表明两种方法得到的信噪比差距是可以接受的，单幅图像法可以替代两幅图像法计算信噪比。当然，若采用不同的磁共振系统及线圈进行分析时，得到的两种方法的关系方程可能会略有差异，这是由于不同的系统的结构噪声会有不同，并且系统磁场的强度会对信噪比有很大的影响，也会将两种方法的差别进行放大和缩小[12]。

经过计算可以看出，两幅图像法的信噪比值高于单幅图像法的信噪比值。这是由于两幅图像法在进行图像相减时消除了系统的结构噪声，使得噪声减小，信噪比增大；而单幅图像法在计算信噪比时，在背景区域的选取上，不可避免的会将非均匀性、伪影等结构噪声选择上，从而造成噪声增加，使得信噪比减小。另外，在磁共振线圈进行临床应用时，磁共振系统的结构噪声是无法消除的，所以采用两幅图像法进行测试线圈信噪比会造成对噪声的低估，而采用单幅图像法更符合实际性。

运用两幅图像法和单幅图像法分别计算信噪比，可以用来对系统质量状况进行评估[13]。例如当两种方法得到的信噪比值差别较小时，可以认为系统稳定性较好；反之，当两种方法得到的信噪比差别较大时，说明系统结构性噪声较大，需要对系统进行调节。

总的来说，两幅图像法更为精确。但单幅图像法操作更简便，不需要辅助软件，而两幅图像还必须要保证两次测试期间系统的稳定性。因此，从实用的角度来说，无论是临床磁共振质量控制或者是对线圈信噪比的测试，采用单幅图像法更便捷。

[1] 张宏杰. 磁共振医学成像射频线圈技术研究[D]. 北京大学，2005

[2] 王龙辰, 朱高杰, 李斌. 磁共振并行成像射频线圈的优化设计进展[J]. 中国医疗器械杂志, 2010, 34(6), 434-435.

[3] J.Rock Hadley. Design of optimal radio frequency coils for improved signal-to-noise ratio in magnetic resonance angiography[D]. The University of Utah, 2006

[4] Olaf Dietrich, Jose G. Raya, Scott B. Reeder, et al. Measurement of signal-to-noise ratios in mr images: influence of multichannel coils, parallel imaging and reconstruction fi lters[J]. J Magn Reson Imaging, 2007,26: 375-385.

[5] Price RR, Axel L, Morgan T, et al. Quality assurance methods and phantoms for magnetic resonance imaging：report of AAPM nuclear magnetic resonance task group no 1[J]. Med Phys，1990, 17: 287-295.

[6] Och JO, Clarke GD, Sobol WT, et a1. Acceptance testing of magnetic resonance imaging systems: report of AAPM Nuclear Magnetic Resonance Task Group No. 6[J]. Med Phys, 1992, 19(1): 217-229.

[7] Kaufman L, Kramer DM, Crooks LE, et al. Measuring signal-tonoise ratios in MR imaging[J]. Radiology, 1989, 173: 265-267.

[8] 朱高杰, 李斌, 魏小二. 基于定量对比方法的磁共振射频线圈的MatLAB图形化性能研究[J]. 中国医疗器械杂志, 2010, 34(3): 180-182.

[9] Firbank MJ, Coulthard A, Harrison RM, et al. A comparison of two methods for measuring the signal to noise ratio on MR images[J]. Phys Med Biol, 1999, 44(12): N261-264.

[10] National Electrical Manufacturers Association (NEMA). Determination of signal-to-noise ratio (SNR) in diagnostic magnetic resonance imaging[R]. NEMA Standards Publication MS 1-2001. Rosslyn: National Electrical Manufacturers Association; 2001. 15p.

[11] J. Martin Bland, Douglas G. Altman. Statistical methods for assessing agreement between two methods of clinical measurement[J]. The Lancet, 1986, 327(8476): 307-310.

[12] Bernd Bittersohl, Tomas Huang, Schneider E, et al. Highresolution mri of the triangular fi bro cartilage complex(TFCC) at 3T: Comparison of surface coil and volume coil[J]. J Magn Reson Imaging, 2007, 26: 701-707

[13] A.M. Di Nallo, O. Ortenzia, M. D Arienzo, et al. MRI quality control tools for procedures and analyses[J]. J Exp Clin Cancer Res, 2006, 25(1): 121-127.

Quantitative Comparison Study on the SNR Method of Phased-array Coil in 3.0 T MRI

【 Writers 】Wang Longchen, Jin Wei , Li Yiming, Li Bin
Dept of Medical Equipment, the Sixth People’s Hospital Af fi liated to Shanghai Jiao Tong University, Shanghai, 200233

SNR, phased-array, radiofrequency coil

R445.2

A

10.3969/j.issn.1671-7104.2013.01.003

1671-7104(2013)01-0010-04

2012-08-21

上海市科委研究基金项目（11441901602）

王龙辰，Email: wanglch666@126.com

李斌，教授级高级工程师，Email: libin2001@hotmail.com

【 Abstract 】In this paper, ACR single image method and NEMA dual-image method were measured SNR using two types of phased-array coils. The correlation equation of the two methods was obtained and substitutability of two methods was analyzed. The results showed that the two methods are replaceable in the evaluation of coils, but the later method gets higher SNR than the fi rst method because structure noise is eliminated..