基于PCA降维和优化核参数SVM的电能质量扰动分类

刘 刚，李凡光

(上海电力学院自动化工程学院，上海 200090)

随着新型电网技术的发展、分布式电源的并网以及用户对电能质量要求的提高，电能质量问题受到越来越多的关注.电力系统规模的日益庞大以及各种电力电子设备、冲击性与非线性负荷的大量投入，导致了电压骤升、电压骤降、电压中断、谐波、暂态脉冲、暂态振荡与电压闪变等一系列电能质量问题[1，2].对电能质量进行监测和分析是发现电能质量问题并进行治理和改善的前提条件，而如何从海量的电能质量扰动信号中自动提取特征并进行正确分类则是电能质量监测分析首先要解决的问题.

文献[3]和文献[4]介绍了人工神经网络应用于电能质量扰动的分类，具有结构简单、求解能力强等优点，但该算法存在局部最优、收敛性差、训练时间长等问题.文献[5]和文献[6]介绍了模糊逻辑在暂态电能质量扰动分类中的应用，通过建立简单明了的“IF-THEN”知识规则进行分类识别，但并不是所有的信号(如暂态振荡、电压波动以及谐波)都具有这种简单的知识规则，这也就限制了模糊逻辑的应用.文献[7]至文献[9]介绍了支持向量机在电能质量扰动分类中的应用，建立在统计学习VC维理论和结构风险最小原理基础上的识别方法，有效地解决了小样本、高维数、非线性等学习问题，并克服了人工神经网络学习的合理结构难以确定和存在局部最优等缺点，提高了学习方法的泛化能力.

本文提出了一种基于主成分分析(Principal Component Analysis，PCA)降维与自适应优化核参数的支持向量机(Support Vector Machine，SVM)相结合的方法，用于电能质量扰动的分类.首先根据电能质量扰动的数学模型获取波形和数据，然后利用多分辨率小波对数据进行分解和重构，提取小波的能量差系数并进行PCA处理，作为特征向量，最后将特征向量输入到支持向量机分类器中，对电能质量扰动进行识别分类.

1 电能质量特征提取

1.1 电能质量扰动信号数学模型的建立

根据IEEE对各类电能质量扰动的定义，本文通过Matlab程序建立正常电压和电压骤升、电压骤降、电压中断、瞬时脉冲、谐波、暂态振荡、电压闪变等电能质量扰动的数学模型，如表1所示.其中T为工频周期，采样频率为6 400 Hz，t1=0.071 s，t2=0.142 s.

表1 电能质量扰动模型

在实际电力系统中的电压信号总是受到不同程度噪音的影响，因此在以上8种电能质量扰动信号模型中叠加信噪比RSN=25 dB的高斯随机白噪音，用以验证支持向量机算法的鲁棒性.含噪的电能质量扰动波形如图1所示.对含噪的电能质量扰动信号采样，共得到200×8组样本数据.

1.2 利用小波能量差提取特征向量

多分辨率分析[10](Multi-Resolution Analy-sis，MRA)是将信号通过高、低通滤波器分别得到信号的高、低频逼近分量，再对低频逼近分量进行分解，得到次高频逼近分量和低频逼近分量，并依此分解下去，最后得到不同尺度下的高频分量系数与最低尺度下的低频分量系数.

根据MRA，采样波形按照不同的分辨率标准来分解，这样每种分解标准下的精确信息的能量计算式为:

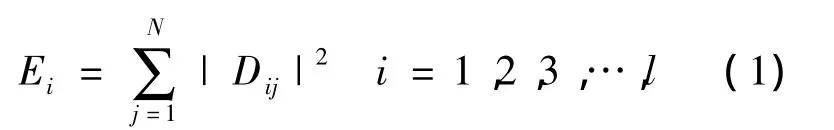
式中:Dij——从基准1到基准l的小波分解的小波系数，Dij=bij，i=1，2，3，…，l;

N——每种标准下系数的总个数;

Ei——分解标准i对应的精确能量.

为了识别不同种类的电能质量干扰，要计算每个分解标准下的能量差，这个差值就是Ei与同种标准下相应的波形的能量Eref(i)之间的差，即

图1 电能质量扰动波形

考虑到电压骤升、暂态脉冲和电压闪变3种扰动信号，本文选择滤波器长度系数为4的db4小波对电压质量扰动信号进行10层分解.根据电能质量信号的小波变换，可以提取扰动信号的能量差系数作为特征向量.

电能质量扰动使信号在各频段上的能量产生了变化，如图2所示.波形都是在5～8层之间发生变化，在7层变化最大，其中暂态脉冲和电压闪变的能量差波形是向上凸起的，其他的是向下凹陷的.

不同类型的电能质量扰动信号能量差分布也是各不相同，可以据此提取信号的小波能量差作为特征向量对电能质量扰动进行识别分类.

图2 电能质量扰动的能量差系数波形

2 用PCA对特征向量进行降维

2.1 主成分分析

主成分分析(PCA)是一种掌握事物主要矛盾的统计分析方法，它可以从多元事物中解析出主要影响因素，以揭示事物的本质，简化复杂的问题.计算主成分的目的是将高维数据投影到较低维空间.PCA主要用于数据降维，目的是找出那些变化大的元素，即方差大的那些维，而去除那些变化不大的维，从而使留下的都是“精品”，同时减小了计算量，提高了计算速度.通过求取样本矩阵的协方差矩阵，求出协方差矩阵的特征向量，而这些特征向量就可以构成这个投影矩阵.

特征向量的选择取决于协方差矩阵的特征值的大小.特征值必须按照从大到小循序排列，并根据特征值大小求出主成分矩阵中的主要元素对原信息的贡献率，根据累计贡献率确定投影矩阵的维数.累计贡献率的大小反应了这种取代的可靠性，累计贡献率越大，可靠性越大，维数也就越高;反之也一样.根据需要，可选择合适的累计贡献率界限，一般要求累计贡献率达到70%以上.

2.2 主成分分析的降维步骤

假设Xm×n是一个m×n(m＞n)矩阵，用PCA对矩阵Xm×n进行降维分析，其步骤如下.

(1)计算矩阵Xm×n的样本的协方差矩阵Sn×n;

(2)计算协方差矩阵Sn×n的特征向量e1，e2，…，eN和对应的特征值x1，x2，…，xN，特征值按从大到小排序.

(3)根据特征值大小计算协方差矩阵的贡献率以及累计贡献率，计算公式为:式中:θi——协方差矩阵Sn×n第i列向量的贡献率;

Θr——协方差矩阵前r列矩阵的累计贡献率.

(4)根据累计贡献率Θr的大小(Θr≥70%)确定投影矩阵(或者称为PCA矩阵)的维数r，其中r≤n.

(5)取协方差矩阵的前r维作为投影矩阵Sn×r，将需要降维的矩阵Ys×n与投影矩阵Sn×r相乘，得到降维后的矩阵Ts×r.

2.3 PCA对小波能量差的降维处理

对电能质量扰动信号采样，共得到200×8组样本数据.小波变换以后，每种扰动的前100组能量差数据组成一个800×10的矩阵X800×10用于训练，后100组能量差数据组成一个800×10的矩阵Y800×10用于分类测试.按照上述步骤对X800×10做 PCA 处理，得到X800×10的协方差矩阵S10×10，特征向量xi，以及特征向量对应的贡献率θi和累积贡献率Θr，如表2所示.

从表2中可以得出累计贡献率Θ3=70.98%＞70%，根据PCA降维的要求，可以取协方差矩阵的前3维作为投影矩阵S10×3.由式(5)可知，可求出降维后的训练样本集H800×3=X800×10S10×3，测试样本集为T800×3=Y800×10S10×3.

表2 协方差矩阵以及累计贡献率%

3 用SVM对电能质量扰动进行分类

3.1 支持向量机的原理

VAPNIK等人在统计学习理论的基础上发展了一种新的模式识别方法——支持向量机(SVM)，在解决小样本、非线性及高维模式识别问题中表现出很大优势.SVM是建立在结构风险最小化原则基础上的机器学习算法，其核心思想是同时控制经验风险和分类器的容量这两个参数，使分类器的分类间隔达到最大，从而使真实风险最小.

在利用SVM对样本进行分类时，可将其分为线性和非线性两种情况，主要工作是寻找问题的分类超平面和最优超平面的判别函数.

在SVM理论中，常用的核函数有线性核函数、多项式核函数、高斯径向基核函数和Sigmoid核函数.

线性核函数表达式为:

多项式核函数表达式为:

高斯径向基核函数表达式为:

Sigmoid核函数表达式为:

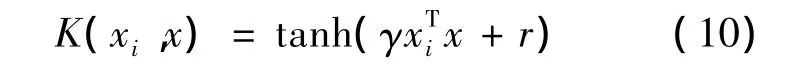
式中:γ＞0;

r，d，σ——核参数.

选择不同形式的核函数就表示采用不同的非线性映射φ(·)，将样本从原空间Rn映射到高维特征空间.

其中，线性核函数适用于数据线性可分的情况，后3种核函数在数据线性不可分的情况下，分类效果较好.在数据线性不可分时，高斯径向基核函数用得较为普遍，分类效果也较好，本文将其选作核函数.

3.2 参数的优化选取和测试集分类

容错惩罚系数c和核参数的选取对分类结果有较大影响，因此要对其进行优化.在使用libsvm对电能质量扰动进行分类时，参数为g=1/(2σ2)，因此对参数c和σ2的选取就转变为对参数c和g的优化选取.本文采用交叉验证[14](K-fold Cross Validation，K-CV)来选择最佳参数c和g.

每种扰动的前100组数据用于libsvm训练和寻找最优参数，后100组数据用于测试分类的准确率.由上文的降维处理可知，PCA降维前，用X800×10训练，用Y800×10测试扰动的分类;PCA 降维后，用H800×3训练，用T800×3测试扰动的分类.因此，参数的优化步骤如下:

(1)粗略地选取c和g的变化范围:2^(-10)，2^(-9)，…，2^(9)，2^(10);

(2)用网格搜索法得到参数对(ci，gj)，i=1，2，…，m;j=1，2，…，n;

(3)对不同参数对进行SVM训练、测试，得到最高分类准确率对应的参数对(cbest，gbest);

(4)根据粗略的选择结果图再进行精细选择c和g的变化范围，寻找最佳的参数对(cbest，gbest).

首先，将PCA降维前的小波能量差系数Y800×10作为特征向量进行参数的优化与扰动的分类，其结果如图3和表3所示.分类所用的时间为13.408 2 s.

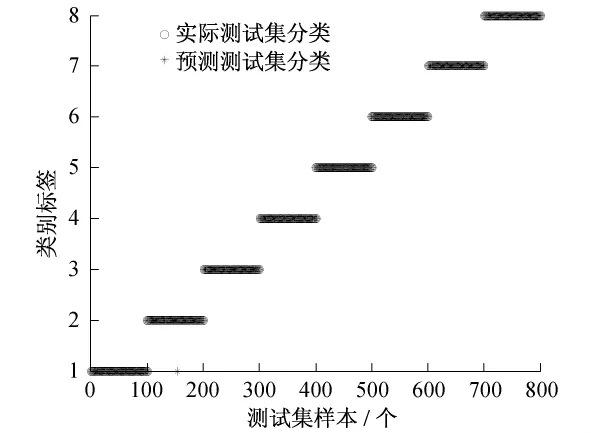
图3 PCA降维前测试集的实际分类和预测分类

表3 PCA降维前电能质量扰动分类结果

将小波能量差系数矩阵用PCA降维处理后形成新的3维矩阵T800×3，将其作为特征向量用于参数的优化选择和扰动的分类，其结果如图4和表4所示.分类所用的时间为5.463 2 s.PCA处理前后分类结果的比较见表5.

从上面的实验结果可知，在PCA降维前，将所有的小波能量差系数数据作为特征向量，用SVM对电能质量扰动进行分类的准确率为99.875%，时间为13.408 2 s;在PCA处理后用3维数据作为特征向量进行分类，分类准确率为96.250%，时间为5.463 2 s.这说明在PCA降维处理后的准确率满足要求的同时，分类速度也得到了提高，3维的小波能量差系数足以代替所有的数据对特征向量进行分类.

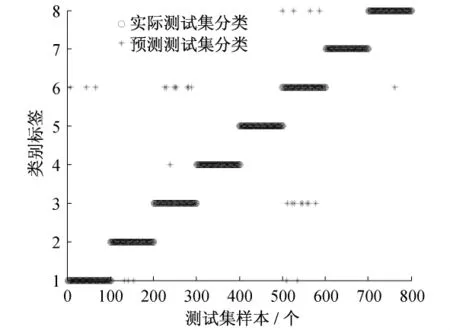
图4 PCA降维后测试集的实际分类和预测分类

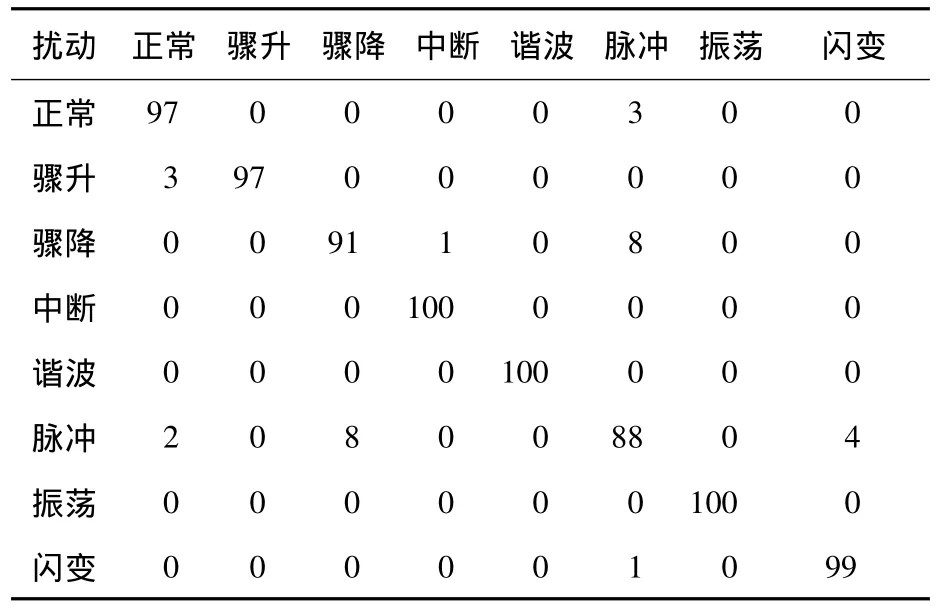
表4 PCA降维后电能质量扰动分类的结果

表5 PCA处理前后分类结果的比较

4 结语

对电能质量扰动分类是在不降低分类准确率的前提下对样本数据进行处理，以提高分类速度.本文使用db4小波对含噪的电能质量扰动信号进行10层分解，提取小波的能量差系数并用PCA进行降维处理，用3维数据作为特征向量，提取了信息的主要成分，除去了冗余信息量.通过对PCA降维前后的特征向量进行分类，得知降维前后的分类准确率都满足要求，而降维后的分类所用的时间远小于降维前的分类时间，这说明用PCA处理后的再分类，能提高分类速度.

[1]程浩忠，艾芊，张志刚.电能质量[M].北京:清华大学出版社，2006:5-12.

[2]ROGER C D，MARK F M，SURYA S，et al.Electrical power systems quality[M].New York:Mc Graw Hill，2002:1-52.

[3]秦英林，田立军.基于小波变换能量分布和神经网络的电能质量扰动分类[J].电力自动化设备，2009，29(7):64-67.

[4]KANITPANYACHAROEAR W， PRERUAEEPREECHACHARN S.Power quality problem classification using wavelet transformation and artificial neural networks[J].IEEE Power Systems Conference and Exposition，2004(3):1 496-1 501.

[5]刘慧芳，陈勇胜，王群，等.基于小波变换和模糊逻辑的暂态电能质量扰动分类[J].电网技术，2008，32(3):84-87.

[6]HUANG Jiansheng，Thong N D.A neural fuzzy classifier for recognition of power quality disturbances[J].IEEE Trans.on Power Delivery，2002，17(2):609-616.

[7]宋晓芳，陈劲操.基于支持向量机的动态电能质量扰动分类方法[J].电力自动化设备，2006，26(4):39-41.

[8]占勇，程浩忠，丁屹峰，等.基于S变换的电能质量扰动支持向量机分类识别[J].中国电机工程学报，2005，25(4):51-56.

[9]LIN W M，WU C H，LIN C H，etal.Detectionand classification omultiple power-quality disturbances with wavelet multiclass SVM [J].IEEE Transactions on Power Delivery，2008，23(4):2 575-2 582.

[10]张凯，关根志，龙望成，等.基于多分辨率标准差及自组织映射网络的电能质量扰动分类识别[J].电力自动化设备，2008，28(8):41-45.

[11]史峰，李洋，王小川，等.MATLAB神经网络30个案例分析[M].北京:北京航空航天大学出版社，2010:112-132.