平底Ⅰ型马蹄形断面临界水深的直接求解
2013-02-26文辉李风玲
文辉,李风玲
(惠州学院建筑与土木工程系,广东惠州 516007)
平底Ⅰ型马蹄形断面临界水深的直接求解
文辉,李风玲
(惠州学院建筑与土木工程系,广东惠州 516007)
平底Ⅰ型马蹄形断面由于其形状及其尺寸容易控制,是水利水电工程中较常采用的断面形式之一,但其临界水深是超越方程,无解析解。为此,通过对平底Ⅰ型马蹄形断面临界流方程进行数学变换,对无量纲临界水深和无量纲参数之间的关系进行研究分析,应用拟合原理得到了平底Ⅰ型马蹄形断面临界水深的近似计算公式。该公式克服了传统的试算法或查表法存在的计算繁琐、依赖图表、误差较大等缺陷。在工程的常用范围内(即临界水深与拱顶半径之比:0<h/r≤1.447 1),该公式表达形式最为简洁,最大误差小于0.4%,将为工程设计及水工设计手册的编制提供参考。
平底Ⅰ型马蹄形断面;临界水深;直接算法
在输水隧洞设计及水力计算中,临界水深是一个控制水流形态变化的关键要素,因此,研究临界流非常重要。主要的断面形式:有压隧洞输水以圆形断面为主,无压输水以梯形、城门洞形和马蹄形过水断面为主。目前国内外学者对梯形[1]、圆形[2-3]、城门洞形[4-6]和马蹄形断面[7-9]的水力计算问题进行了深入的研究,也得到了不少简捷计算公式,解决了不少工程实际问题。平底Ⅰ型马蹄形断面作为标准Ⅰ型马蹄形断面的简化型,将底拱改为了平底。它适合于基底压力不大的地质情况,具有施工尺寸容易控制和受力条件好等优点,是广泛采用的断面形式之一。但对于这一断面形式的水力计算研究尚未见报道。为此,本文通过对平底Ⅰ型马蹄形断面临界水深基本方程进行数学变换,引入无量纲参数,并对无量纲临界水深和无量纲参数之间的关系进行研究分析;依据给水排水工程规范及水利工程规范等要求,考虑工程实际中的常用范围,确定公式的应用范围,应用拟合原理得到了平底Ⅰ型马蹄形断面临界水深的近似计算公式。
1 平底Ⅰ型马蹄形断面的水力要素和临界水深基本方程
1.1 平底Ⅰ型马蹄形断面形式
平底Ⅰ型马蹄形断面是由平底、圆弧侧拱和圆弧顶拱而构成,见图1。
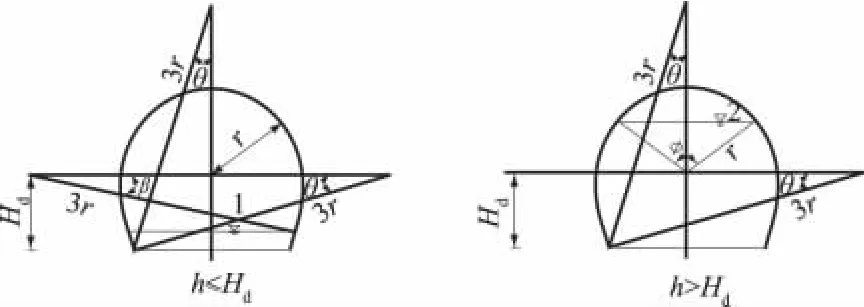
图1 平底Ⅰ型马蹄形断面Fig.1Ⅰ-Type horseshoe cross-section with flat-bottom
1.2 临界水深的基本方程

式中:Q为过水流量(m3/s);α为流速分布不均匀系数(本文取1.0);g为重力加速度(9.81 m/s2);AK为相应于临界水深时的过水断面面积(m2);BK为相应于临界水深时的水面宽度(m)。
1.3 平底Ⅰ型马蹄形断面不同水深的水力要素
由于平底Ⅰ型马蹄形断面的几何特点,临界水深处于2种不同范围时其水力要素计算公式是不同的,具体见表1。
2 平底Ⅰ型马蹄形断面临界水深的计算公式
2.1 分界流量的确定
只有首先确定了分界流量,才能根据流量判别临界水深将位于的范围,从而选定相应的计算公式,得出正确的结果。计算特征点水深h=Hd时,对应的流量即为分界流量QD。

表1 水力要素计算公式Table 1Calculation equations for hydraulic elements
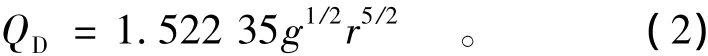
2.2 平底Ⅰ型马蹄形断面临界水深的近似计算公式
为了方便研究,令

式中:K为参数;X为无量纲临界水深。
2.2.1 K参数的上限值KU
根据SL279—2002水工隧洞设计规范,为了保证无压隧洞能在水位变化情况下仍能保持无压流状态,要求通过最大流量时洞内水面以上的空间面积不小于隧洞横断面面积的15%。即为平底Ⅰ型马蹄形断面面积。也即

该方程为三角超越方程,试算解得ø=1.913 3,KU=12.756 58。
1.3.1 对照组 采取硝苯地平(四川德峰药业有限公司,国药准字:H21023054)治疗:予以硝苯地平10 mg/次,3次/d,口服。
2.2.2 K参数的分界值KD
临界水深对应于特征点水深h=Hd时,KD= 2.317 56,通过进行大量试算,并采用编程逐步优化拟合的方法,得出无量纲临界水深的近似计算公式:
当Q≤QD时,水深位于断面下半部,即0<hK≤ Hd,

当QD>Q时,水深位于断面上半部,即Hd<hK≤HU,


3 公式评价
将公式(4)和公式(5)的计算误差列于表2。
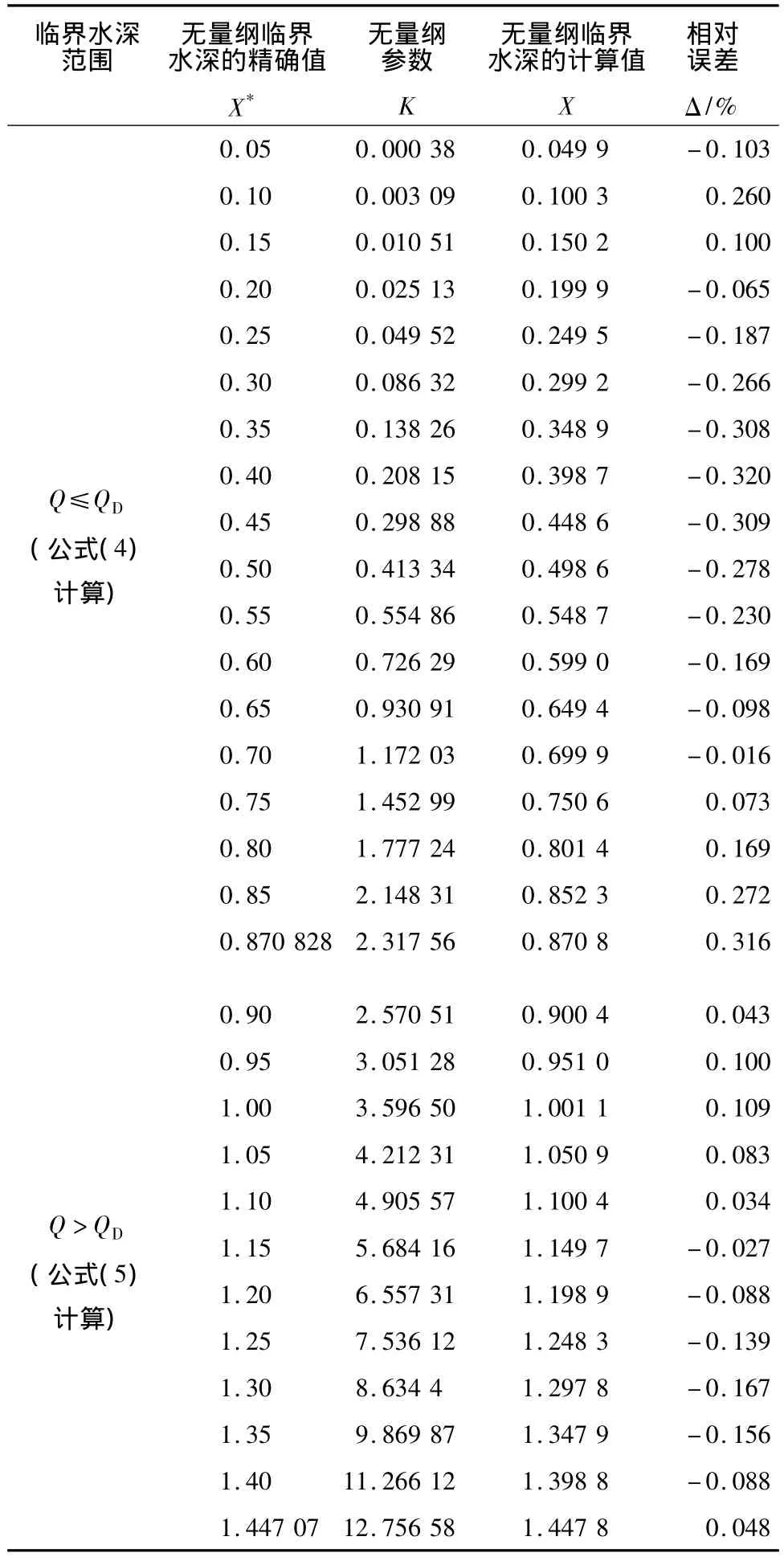
表2 公式(4)和公式(5)误差分析Table 2Distribution of relative errors by using formula(4)and formula(5)
公式(4)和公式(5)为形式简单的幂函数型,最大相对误差为0.4%,完全满足工程设计需要。
4 计算步骤及应用举例
4.1 计算临界水深步骤
①由式(2)求分界流量QD;②由式(3)求参数K;③判别应用公式由式(4)或式(5)求得无量纲临界水深X;④由式(3)求得临界水深hK。
4.2 算例
先求界限流量:
由式(2)求分界流量QD=1.522 35g1/2r5/2= 47.12 m3/s。
当Q=60 m3/s时,Q>QD,

由式(3)得hK=X·r=2.537 m,(精确值: 2.534 m),则相对误差为0.105%。
当Q=35 m3/s时,Q≤QD,
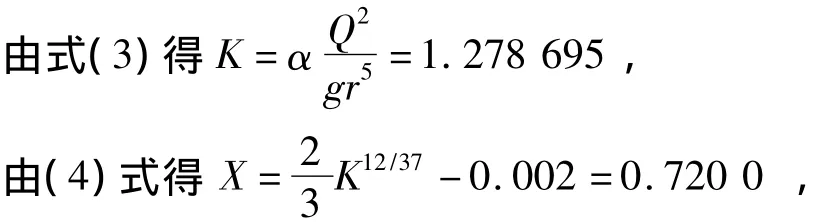
由(3)式得hK=X·r=1.800 0 m,(精确值: 1.799 7 m),相对误差为0.018%。
5 结语
(1)本文提出的近似公式具有形式简捷、实用方便的特点,且在工程适用范围内公式最大相对误差的绝对值为0.4%,满足工程实际的需要。综上所述,本文公式是值得推荐的。
(2)在实际工程中由于地质地形、工程施工等边界条件的不同,对于各种类型马蹄形断面隧洞,还要继续研究适用范围更广、更好的新算法。
[1]赵延风,祝晗英,宋松柏,等.论梯形明渠临界水深的精确计算公式[J].长江科学院院报,2009,26(4): 18-21.(ZHAO Yan-feng,ZHU Han-ying,SONG Songbai,et al.Discussion on Accurate Calculation Formula of Critical Depth of Open Trapezoidal Channel[J].Journal of Yangtze River Scientific Research Institute,2009,26 (4):18-21.(in Chinese))
[2]文辉,李风玲,彭波,等.圆管明渠临界水深的直接近似计算公式[J].人民黄河,2007,29(4):67-68. (WEN Hui,LI Feng-ling,PENG Bo,et al.Direct Approximate Formula for Critical Depth of Pipe-channel[J]. Yellow River,2007,29(4):67-68.(in Chinese))
[3]李风玲,文辉,彭波.圆形过水断面临界流的近似水力计算[J].人民长江,2008,39(11):77-78.(LI Feng-ling,WEN Hui,PENG Bo.Approximate Hydraulic Calculation for Critical Flow in Circular Cross-section[J].Yangtze River,2008,39(11):77-78.(in Chinese))
[4]张宽地,王光谦,吕宏兴,等.明流条件下城门洞形隧洞临界水深的直接计算法[J].四川大学学报(工程科学版),2010,42(3):101-106.(ZHANG Kuan-di,WANG Guang-qian,LV Hong-xing,et al.A Direct Method for Calculating the Critical Depth of a Arched Section Tunnel[J].Journal of Sichuan University(Engineering Science Edition),2010,42(3):101-106.(in Chinese))
[5]赵延风,宋松柏,孟秦倩.普通城门洞形断面临界水深的近似计算方法[J].长江科学院院报,2008,25(4): 14-15.(ZHAO Yan-feng,SONG Song-bai,MENG Qinqian.Approximate Method Calculating Critical Water Depth in Common City-opening Shaped Cross-section[J].Journal of Yangtze River Scientific Research Institute,2008,25(4):14-15.(in Chinese))
[6]文辉,李风玲.再论城门洞形断面隧洞临界水深的近似计算[J].人民长江,2009,40(11):78-79. (WEN Hui,LI Feng-ling.Further Discussion on the Approximate Calculation of Critical Depth of an Arched Tunnel Section[J].Yangtze River,2009,40(11):78-79. (in Chinese))
[7]文辉,李风玲,李霞.标准Ⅰ型马蹄形断面正常水深的近似算法[J].人民黄河,2008,30(7):89-90. (WEN Hui,LI Feng-ling,LI Xia.Approximate Solution on Normal Depth of Standard I Type Horseshoe Section Tunnel[J].Yellow River,2008,30(7):89-90.(in Chinese))
[8]王正中,陈涛,卢琴,等.马蹄形断面隧洞临界水深的直接计算[J].水力发电学报,2005,24(5):95-98.(WANG Zheng-zhong,CHEN Tao,LU Qin,et al. The Direct Solution on Critical Depth of Horseshoe Section Tunnel[J].Journal of Hydroelectric Engineering,2005,24(5):95-98.(in Chinese))
[9]张宽地,吕宏兴,陈俊英.马蹄形过水断面临界水深的直接计算法[J].长江科学院院报,2008,25(4):15-18.(ZHANG Kuan-di,LV Hong-xing,CHEN Jun-ying. Direct Calculation of Critical Depth of Horseshoe Section Tunnel[J].Journal of Yangtze River Scientific Research Institute,2008,25(4):15-18.(in Chinese))
(编辑:刘运飞)
Direct Solution to the Critical Depth of I-Type Horseshoe Cross-Section with Flat Bottom
WEN Hui,LI Feng-ling
(Department of Architecture and Civil Engineering,Huizhou University,Huizhou516007,China)
I-type horseshoe cross-section with flat-bottom is simplified from standard I-type horseshoe cross-section. It is composed of a flat-bottom and three arc sections.Since the shape and size are easy to control,it is commonly applied in hydroelectric engineering.But the critical water depth computation formula is a transcendental equation and has no analytic solution.Mathematics transformation for the critical flow equation was performed,and the relationship between the dimensionless critical water depth and the relative dimensionless parameters was analyzed. Furthermore,an approximate formula for the calculation of critical water depth for I-type horseshoe cross-section with flat-bottom tunnel was obtained according to the fitting principle.This method overcomes the defects of other iterative trial calculating methods,such as calculation step,dependence on special charts and curves,and serious error.The formula is simple and the maximum error is less than 0.4%under the general engineering design condition(0<h/r≤1.447 1,h/r is the ratio of critical depth to the radius of arch roof).It can be used for engineering design practice and for the compilation of hydraulic structure design handbooks.
I-type horseshoe cross-section with flat-bottom;critical water depth;direct calculation formula
TV131.4
A
1001-5485(2013)04-0040-04
10.3969/j.issn.1001-5485.2013.04.009 2013,30(04):40-43
2012-01-31;
2012-04-05
惠州学院引进教授、博士科研启动基金项目(C510.0211)
文辉(1963-),男,四川射洪人,教授,主要从事水力学教学和研究,(电话)13928325682(电子信箱)wenhui-hzu@163.com。
