δ/θ型相关解扩抑制多址干扰的能力分析❋
2013-02-25龙德浩陈志清
龙德浩,陈志清
(1.四川大学,成都 610064;2.成都大学,成都 610106)
δ/θ型相关解扩抑制多址干扰的能力分析❋
龙德浩1,❋❋,陈志清2
(1.四川大学,成都 610064;2.成都大学,成都 610106)
龙德浩、陈志清提出的δ/θ型基带相关检测/解扩方案(《电讯技术》2012年第9期1438-1442页),相对于经典相关解扩,其计算量减少了99.61%,且抗干扰能力较强,但定量分析不足。鉴于此,基于大数定理,分别对VIVS准混沌、m和Walsh等3种扩频码阵列进行了仿真相关解扩。结果表明:在给定AWGN条件下,当多址干扰分别为400条、350条和924条时,δ/θ相关解扩较经典相关解扩的BER减小了2~3个数量级。
CDMA系统;多址干扰抑制;多用户干扰抑制;δ/θ相关解扩
1 问题的提出
基于龙德浩、陈志清提出的“相关解扩三要素”所导出的δ/θ相关解扩方案[1],其特点是:①计算量较小,当扩频系数L=256时,较经典相关解扩,其计算量减小了(L-1)/L=99.61%;②抗干扰能力较强,当经典基带相关解扩有效时,本方案同样有效;当经典失效时,在一定干扰条件下本方案仍然有效。显然,这里“抗干扰能力较强”一词尚属定性结论。为了工程应用,必须定量分析。由图1~3知,依照适用δ/θ-相关解扩的扩频码检验方法[2],VIVS准混沌、m和Walsh等3种扩频码阵列所产生的3组零时延互相关函数值的概率密度函数,统计平均值m与统计标准差v是不相同的,因而,抑制干扰的能力是不可能相同的。那么,孰优孰劣呢?本文将在给定加性正态白噪声干扰AWGN(例如AWGN=6×randn(1,n))条件下,借助计算机仿真技术,分别对此3个扩频码阵列定量地探讨δ/θ相关解扩方案抑制“AWGN+多址干扰”的能力,并与经典相关解扩的结果进行比较。

图1 VIVS零时延互相关函数值的概率密度:c6002-512(600×4096)Fig.1 VIVS zero-delay cross-correlation value
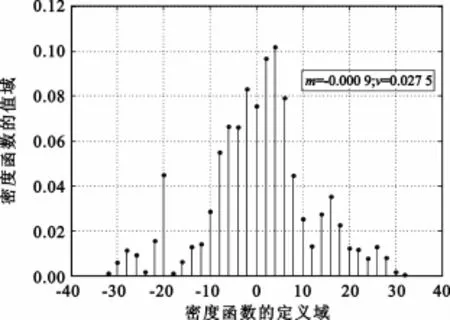
图2 m阵列零时延互相关函数值的概率密度:s(600×1024)Fig.2 m zero-delay cross-correlation value of the density function:c6002-512(600×4096)of the density function:s(600×1024)

图3 Walsh零时延互相关函数值的概率密度:walsh(600×1024)Fig.3 Walsh zero-delay cross-correlation value of the density function:Walsh(600×1024)
2 δ/θ型相关解扩抑制“AWGN+MAI”的能力
说明:当输入干扰较弱时,经典相关函数是满足“相关解扩三要素”的[1],故δ/θ相关解扩与经典相关解扩都工作良好,不存在抗干扰问题。鉴于此,为了减小仿真的计算量,本文探讨干扰较强时“δ/θ相关解扩”与“经典相关解扩”的抗干扰能力,即平均比特误码率(BER)的大小。
设置门限电平的目的:旨在使“最佳扩频码阵列”的相关检测/解扩的BER最小。
确定相关解扩门限电平的基本原则:被采用的“扩频码检验方法”与其“相关解扩的相关函数”,必须同时满足如下两个必要条件:一是“扩频码检验方法”与其“相关解扩的相关函数”的结构特征及其统计特征必须一一对应、相互匹配,我们称之为原则Ⅰ;二是门限电平Vm必须与决定扩频码阵列检验成败的关键参数(例如,δ=max(δa,δc),δ0,等)密切相关[2-3],我们称之为原则Ⅱ。
被检对象:θ基带相关解扩方案[1]。显然,这是δ/θ相关解扩方案的特例。
(2)θ相关函数的结构特征是:满足“相关解扩三要素”,即有峰值、无旁瓣、不存在旁瓣干扰[1]。
(3)θ相关解扩的门限电平。
定理1:δ/θ相关解扩的通用门限电平Vm=δ0。
定理2:最佳扩频码阵列的δ/θ相关解扩的最佳门限电平Vm=0。
证明:由文献[2]推论1和定理4得知,因为最佳扩频码阵列的δ0=0,故“最佳扩频码阵列”(例如Walsh正交扩频码阵列)的δ/θ相关解扩的最佳门限电平Vm=δ0=0。至此,本定理得证明。
定理3:非最佳扩频码阵列的δ/θ相关解扩的次最佳门限电平Vm是自适应的。

定理4:δ/θ相关自适应门限解扩与δ/θ相关最佳门限解扩的关系。
证明:显然,δ/θ相关自适应门限解扩,较经典固定门限Vm=δ0≠0相关解扩,平均比特误码率BER更小,但前者每解扩±1比特都必须自动更新一次门限电平Vm或Vm-,因此,更新“自适应门限电平Vm”的计算量较大。如何减小其计算量?就“乘法”扩频而言,因为δ/θ相关解扩属于极性判决,故可以用“零”门限电平的δ/θ相关解扩替代自适应门限电平的δ/θ相关解扩。但必须说明,这种替代方法只能减少形成自适应门限电平所需的计算量及其存储单元,并不能提高非最佳扩频码阵列的δ/θ相关解扩的抗干扰能力。
参考对象:经典相关解扩方法。
(1)经典相关函数r(τ)的形成方法:[r(τ),lags]=xcorr(ai,si,biased),
τ∈lags=2×n-1;si=mp*ai*(±1)+n1,其中,n1=Jnor+JMA;注意参数biased。
(2)经典相关函数r(τ)的结构特征是:不满足“相关解扩三要素”,即有峰值、有旁瓣、存在旁瓣干扰[1]。
(3)经典相关解扩的门限电平
定理5:经典相关解扩的自适应门限电平。
证明:当干扰较强时,因为经典相关函数r(τ)的结构特征:不满足“相关解扩三要素”,即有峰值、有旁瓣、始终存在着旁瓣干扰。故经典相关解扩方法与经典扩频码检验方法[3]的结构特征及其统计特征是一一对应、相互匹配的,即满足设置相关解扩门限电平Vm的基本原则Ⅰ。又,经典相关解扩方法与经典扩频码检验方法的4个参数:被检‘±1’随机矩阵的结构特征行数M和列数L,及其统计特征行自相关函数旁瓣的绝对最大值δa和行互相关函数的绝对最大值δc的定义是完全相同的,故当M和L给定时,δ是决定经典扩频码检验成败的关键参数。参见δa、δc和δ=max(δa,δc)的定义,与关键参数δ密切相关的正好是max(r(τ≠0))或min(r(τ≠0)),故依照设置“门限电平”的基本原则Ⅱ,经典相关解扩的自适应门限电平是:解扩‘+1’时,Vm=max(r(τ≠0)),如文献[1]的图1(b)所示;解扩‘-1’时,Vm-=min(r(τ≠0)),如文献[1]的图2(b)所示。这里,经典相关自适应门限解扩的含义是:每解扩一个‘+1’或‘-1’都自动更新一次r(τ≠0)及其门限电平Vm或Vm-。
很遗憾,迄今为止,尚未找到适用于经典相关解扩的最佳经典扩频码检验方法及其阵列,因此,在目前情况下,尚不可能导出最佳经典相关解扩方案。
参考噪声:n1=Jnor+JMA=sn*randn(1,n)+多址干扰码mul。
信/噪比:
(1)Psn(j)=10*lg10(cov(a1*(+1))/cov(n1)),解扩‘+1’的输入平均功率信噪比;
(2)Psn-(j)=10*lg10(cov(a1*(-1))/cov(n1)),解扩‘-1’的输入平均功率信噪比。
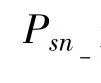
统计依据:大数定理。
函数说明:P-despreaded3mult(c,m,n,m1,sn,du,mul,mp)
目的:比较“经典相关解扩与θ相关解扩”的平均比特误码率BER。
参数:
c:待检‘±1’扩频码矩阵,例如VIVS变初值变结构准混沌矩阵c6002-512(6002×4096),m矩阵s1024(1024×1024),Walsh(Pale型)矩阵walsh1024m(1024×1024);
m:c的行数;
n:c的列数;
m1:被检测的行数,即被检用户地址码数,m1<m,本文m1=100;
sn:控制相关解扩输入信噪比Psn和Psn-的常数,sn*randn(1,n),本文sn=6;
du:扩频-解扩的信息序列,本文采用的是u1,长度1 024的‘±’序列;
mul:多址干扰数;
mp:控制相关器输入有用信号的幅度,旨在模拟“吸收”或“衰落”,常态mp=1。
注意:为了loglog比特误码率的图形清晰可视,按照对数的定义,误码概率pc=1-p必须大于零。因此,当解扩概率p=1.000 0时,程序中已更改为p=0.999 9。故本文比特误码率图形中10-4的含义是正确解扩的真实概率可能是1.000 0,亦可能是0.999 9。
2.1 关于VIVS阵列的δ/θ型相关解扩抑制“AWGN+MAI”的能力
调用函数:P-despreaded3nmamp(c6002-512,6002,4096,100,6,u1,400,1)。
相关参数详见函数说明。
c是VIVS变初值变结构准混沌‘±1’矩阵c6002-512(6002×4096)。表1是VIVS的经典相关解扩与θ相关解扩的统计结果。
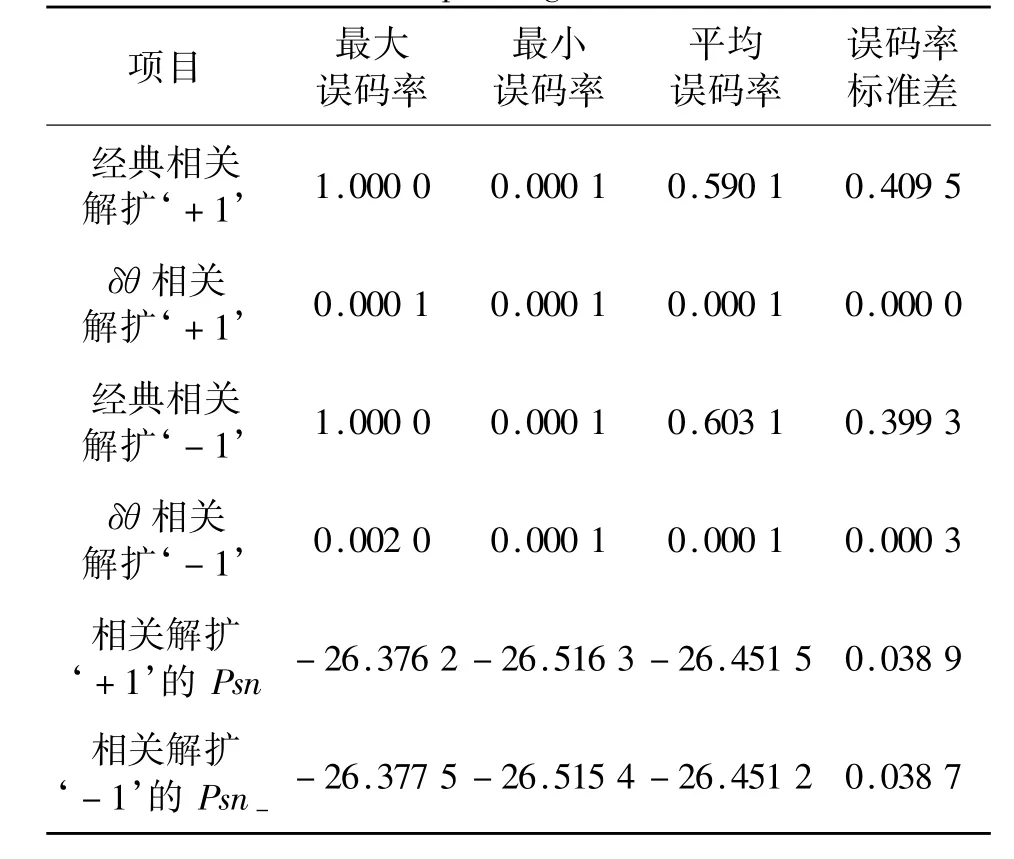
表1 VIVS的经典相关解扩与θ相关解扩的统计结果Table 1 VIVS classic correlation despreading andθ correlation despreading statistical results
由表1得知,因为干扰较强,SNR≈-26.451 5 dB,即干扰(AWGN:6*randn(1,4096)+VIVS多址干扰:400条)较本地码ai的功率大了441.72倍。在这种情况下,即使作用于接收机所有信号的功率都完全相等,经典相关函数如文献[1]的表1和图1(b)与图2(b)所示也依然是不满足“相关解扩三要素”,即有峰值、有旁瓣,且“零时延”的有用峰值信号完全被严重的旁瓣干扰所淹没,故对VIVS阵列c6002-512来说,经典相关解扩已深深陷入失效状态,其仿真结果是:平均比特误码率BER太大,分别是0.590 1和0.603 1;而θ相关函数如文献[1]的表1和图1(f)与图2(f)所示,却满足“相关解扩三要素”,即有峰值、无旁瓣,尽管有用峰值信号幅度不高,但不存在旁瓣干扰,故对VIVS阵列c6002-512来说,θ相关解扩工作正常,其仿真结果是平均比特误码率BER较小,分别为0.000 1和0.000 1。相对于经典相关解扩,其BER降低较显著。
小结1:在给定干扰(AWGN:6*randn(1,4096)+VIVS多址干扰:400条)条件下,对于VIVS阵列依次处理了m1=100对CDMA多址用户,每对用户收发了1 024比特信息,共计处理了m1×length(u1)=100×1024=102 400个数据。因为此数据量较大,故在大数定理意义下,对VIVS阵列c6002-512仿真解扩的结果如表1和图4所示是可信的;由此导出的4个实用参数如表2所示也是可信的。

图4 VIVS经典相关解扩与δ/θ相关解扩的误码率:正态6+多址400Fig.4 VIVS classiccorrelation dispreading andδ/correlation despreading BER:Normal 6+Multiple-Access 400

表2 θ相关解扩较经典相关解扩的BER的降低状况(VIVS)Table 2θcorrelation despreading relative to classic correlation despreading BER reduction conditions(VIVS)
2.2 关于m阵列的δ/θ型相关解扩抑制“AWGN+MAI”的能力
调用函数:P-despreaded3nmamp(s1024,1024,1024,100,6,u1,350,1)。
相关参数:详见函数说明。
c是m线性反馈移位寄存器‘±1’矩阵s1024(1024×1024)。表3是s1024的经典相关解扩与θ相关解扩的统计结果。

表3 s1024的经典相关解扩与θ相关解扩的统计结果Table 3 S1024 classic correlation despreading and θcorrelation despreading statistical results
由表3得知,因为干扰较强,SNR≈-24 dB,即干扰(AWGN:6*randn(1,1024)+m多址干扰:350条)较本地码ai的功率大了277倍。在这种情况下,即使作用于接收机所有信号的功率都完全相等,经典相关函数如文献[1]的表1和图1(b)与图2(b)所示也仍然是不满足“相关解扩三要素”,即有峰值、有旁瓣,且“零时延”的有用峰值信号完全被严重的旁瓣干扰所淹没,故对m阵列s1024来说,经典相关解扩已深深陷入失效状态,其仿真结果是平均误码率太大,分别是0.964 0和0.800 0;而θ相关函数如文献[1]的表1和图1(f)与图2(f)所示,却满足“相关解扩三要素”,即有峰值、无旁瓣,尽管有用峰值信号幅度不高,但不存在旁瓣干扰,故对m阵列s1024来说,θ型相关解扩工作正常,其仿真结果是平均误码率较小,分别为0.000 3和0.000 1。相对于经典相关解扩,其BER降低较显著。
小结2:在此干扰(AWGN:6*randn(1,1024)+m多址干扰:350条)条件下,对m阵列依次处理了m1=100对CDMA多址用户,每对用户收发了1 024比特信息,共计处理了m1×length(u1)=100×1024=102 400个数据。因为此数据量较大,故在大数定理意义下,对m阵列s1024仿真解扩的结果如表3和图5所示是可信的;由此导出的4个实用参数如表4所示也是可信的。

图5 s1024经典相关解扩与δ/θ相关解扩的误码率:正态6+多址350Fig.5 S1024 classic correlation despreading andδ/θcorrelation despreading BER:Normal 6+Multiple-Access 350

表4 θ相关解扩较经典相关解扩的BER的降低状况(s1024)Table 4θcorrelation despreading relative to classic correlation despreading BER reduction conditions(s1024)
2.3 关于Walsh正交阵列的δ/θ型相关解扩抑制“AWGN+MAI”的能力
调用函数:P-despreaded3nmamp(walsh1024m,1024,1024,100,6,u1,924,1)。
相关参数:详见函数说明。
c是Walsh(Pale型)‘±1’正交矩阵walsh1024m(1024×1024)。表5是walsh1024m的经典相关解扩与θ相关解扩的统计参数。
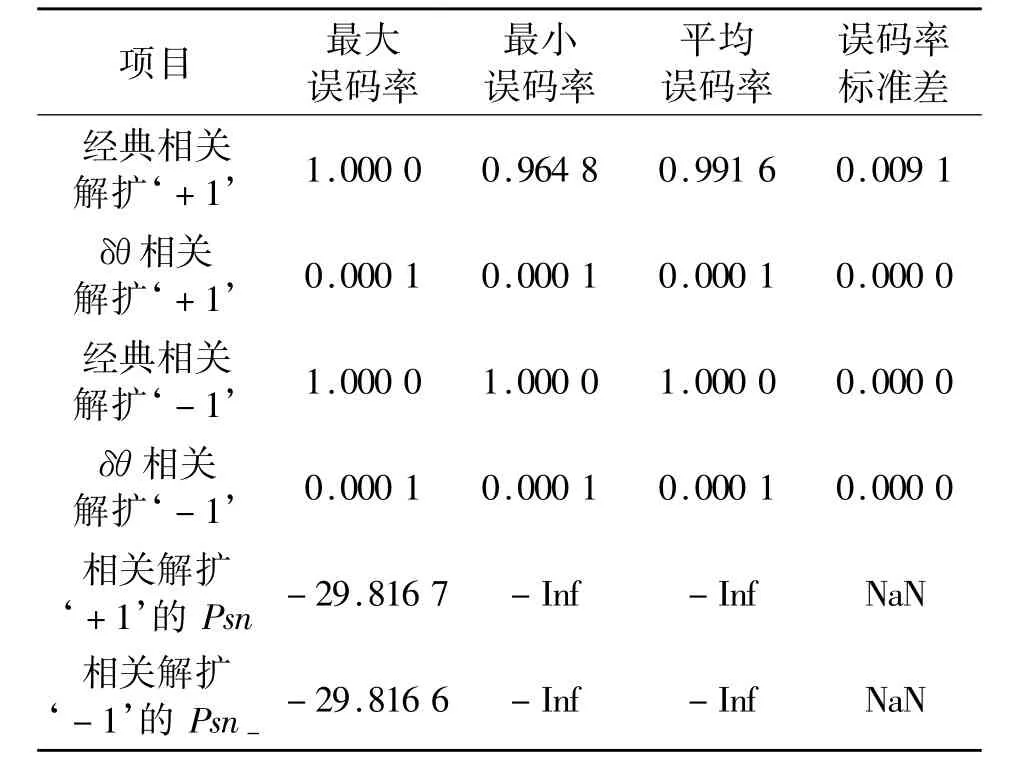
表5 walsh1024m的经典相关解扩与θ相关解扩的统计参数Table 5 Walsh1024m classic correlation despreading and θcorrelation despreading statistical results
由表5得知,因为干扰较强,SNR≈-29.816 7 dB,即干扰(AWGN:6*randn(1,1024)+Walsh多址干扰码:924条)较本地码ai的功率大了958倍。在这种情况下,即使作用于接收机所有信号的功率都完全相等,经典相关函数如文献[1]的表1和图1(b)与图2(b)所示也依然是不满足“相关解扩三要素”,即有峰值、有旁瓣,且“零时延”的有用峰值信号完全被严重的旁瓣干扰所淹没,故对Walsh阵列walsh1024m来说,经典相关解扩已深深陷入失效状态,其仿真结果是平均误码率太大,分别为0.991 6和1.000 0;而θ相关函数如文献[1]的表1和图1(f)与图2(f)所示,却满足“相关解扩三要素”,即有峰值、无旁瓣,尽管有用峰值信号幅度不高,但不存在旁瓣干扰,故对于Walsh阵列walsh1024m来说,θ型相关解扩运行正常,其仿真结果是平均误码率较小,分别为0.000 1和0.000 1。相对于经典相关解扩,其BER降低较显著。
小结3:在此干扰(AWGN:6*randn(1,1024)+Walsh多址干扰码:924条)条件下,对walsh1024m阵列依次处理了m1=100对CDMA多址用户,每对用户收发了1 024比特信息,共计处理了m1× length(u1)=100×1024=102 400个数据。因为此数据量较大,故在大数定理意义下,对于Walsh阵列walsh1024m来说,仿真解扩的结果如表5和图6所示是可信的;由此导出的4个适用参数如表6所示也是可信的。

图6 Walsh经典相关解扩与δ/θ相关解扩的误码率:正态6+多址924Fig.6 Walsh1024m classic correlation despreading andδ/θ correlation despreading BER:Normal 6+Multiple-Access 924
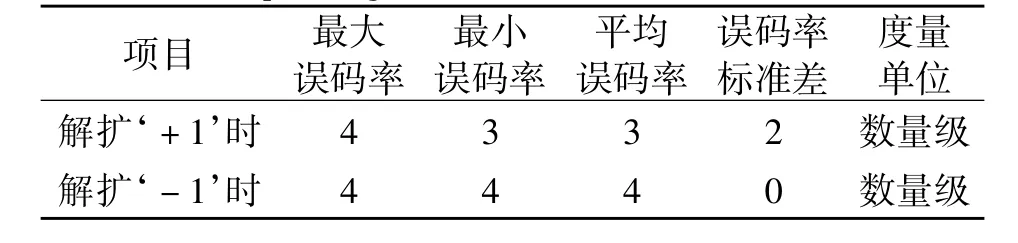
表6 θ相关解扩较经典相关解扩的BER的降低状况(walsh1024m)Table 6 θcorrelation despreading relative to classic correlation despreading BER reduction conditions(walsh1024m)
3 结束语
综上所述,可以得出以下结论。
(1)相关解扩抗多址干扰的能力与相关函数的结构特征和统计特征密切相关。特别地,基于“相关解扩三要素”所导出的δ/θ相关解扩,较经典相关解扩抗多址干扰的能力更强:在相同输入SNR条件下,其BER降低了2~3个数量级(详见表2、表4和表6)。
(2)在δ/θ相关解扩意义下,Walsh扩频码阵列抗多址的能力最强,达到了理论极限(详见表3和表5)。此结果与文献[2]的定理4及图2~3的物理涵义完全一致;换言之,龙德浩、陈志清所提出的上述“确定相关解扩门限电平的基本原则”是合理的,由此“基本原则”所导出的CDMA系统相关解扩门限电平Vm达到了本文的初衷——“最佳扩频码阵列”的最佳门限电平Vm=δ0=0的δ/θ相关解扩的BER是最小的。
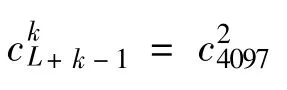
(4)δ/θ型相关检测/解扩的适用对象为一切经典相关检测/解扩的场合,例如扩频移动通信、扩频局域网、扩频无人机及扩频雷达,等。适用条件为比特同步,与经典相关解扩的相同。适用结果较经典相关检测/解扩有3个特点:一是抗干扰能力提高了2~3个数量级(详见表4和表6);二是检测/解扩的计算量减少了或检测/解扩的速率提高了2个数量级,因而,对于某些抢“先”即“生存”的火控雷达、反隐身雷达、机场空中管理雷达、生命探测雷达等可能赢得一线生存的机会;三是可靠性更高,耗电量更少,成本更低(详见文献[1])。
参考文献:
[1]龙德浩,陈志清.δ/θ型基带相关检测/解扩方案[J].电讯技术,2012,52(9):1438-1442. LONG De-hao,CHEN Zhi-qing.δ/θBase Band Correlation Detection/Despreading Scheme[J].Telecommunication Engineering,2012,52(9):1438-1442.(in Chinese)
[2]龙德浩,陈志清.用于δ/θ型相关解扩的扩频码检验方法[J].电讯技术,2012,52(10):1630-1634. LONG De-hao,CHEN Zhi-qing.Spreading Code Test forδ/θ Correlation Despreading[J].Telecommunication Engineering,2012,52(10):1630-1634.(in Chinese)
[3]PENG Dai-yuan,FAN Ping-zhi.New theoretical bounds on the aperiodic correlation functions of binary sequences[J]. Science in China Ser.F Information Sciences,2005,48(1):28-45.

龙德浩(1938—),男,四川乐至人,1961年于四川大学无线电系获学士学位,现为四川大学退休教授,主要研究方向为信息基础理论;
LONG De-hao was born in Lezhi,Sichuan Province,in 1938.He received the B.S.degree from Sichuan University in 1961.He is now a retired professor.His research direction is information basic theory.
Emial:longdehao9@gmail.com
陈志清(1943—),女,四川犍为人,1965年于四川大学数学系获学士学位,现为成都大学退休教授,主要研究方向为应用数学。
CHEN Zhi-qing was born in Qianwei,Sichuan Province,in 1943.She received the B.S.degree from Sichuan University in 1965.She is now a retired professor.Her research direction is applied mathematics.
Analysis ofδ/θCorrelation Despreading′s Ability to Suppress M ultiple-access Interference
LONG De-hao1,CHEN Zhi-qing2
(1.Sichuan University,Chengdu 610064,China;2.Chengdu University,Chengdu 610106,China)
The computation burden ofδ/θbase band correlation detection/despreading scheme proposed by LONG De-hao and CHEN Zhi-qing in Telecommunication Engineering(No.9,2012,Page 1438-1442),is reduced by 99.61%relative to the classical correlation detection/despreading,and its anti-interference ability is stronger,but quantitative analysis is insufficient in that paper.In view of this,based on the law of large numbers,three spreading code arrays(VIVS quasi-chaotic,m and Walsh)are performedδ/θcorrelation despreading respectively through simulation,and the results show that the BER of theδ/θdespreading is reduced 2 to 3 orders of magnitude relative to the classical correlation despreading in the conditions of given AWGN while the number of multiple-access interference is 400,350 and 924,respectively.
CDMA system;multiple-access interference suppression;multi-user interference suppression;δ/θ correlation despreading
longdehao9@gmail.com
TN914.4;TN914.5
A
1001-893X(2013)05-0553-07
10.3969/j.issn.1001-893x.2013.05.005
2012-11-15;
2013-05-10 Received date:2012-11-15;Revised date:2013-05-10
❋❋
longdehao9@gmail.com
