电各向异性色散介质电磁散射时域有限差分分析的半解析递推卷积方法*

王飞 魏兵

(西安电子科技大学物理系,西安 710071)

(2012年7月8日收到;2012年9月26日收到修改稿)

1 引言

近年来,等离子体与电磁波的相互作用受到了人们的广泛关注.鉴于等离子体介质的色散特性以及实际问题的复杂性,其与电磁波的相互作用常常采用数值的方法进行分析.时域有限差分( finite difference time domain,FDTD)方法长于处理复杂介质的电磁问题,因此常采用FDTD方法仿真等离子体与电磁波的相互作用.文献中处理各向同性色散介质电磁问题的FDTD方法有：递归卷积(recursive convolution,RC)法[1]、分段线性递归卷积(piecewise linear recursive convolution,PLRC)法[2]、电流密度卷积(current density convolution,JEC)法[3]、分段线性电流密度递归卷积(piecewise linear current density recursive convolution,PLJERC)法[4,5]、辅助方程(auxiliary differential equation,ADE)法[6,7]、Z变换 (Z-transform)法[8-10]、移位算子(shift operator,SO)法[11]和半解析递推卷积(semi-analytical recursive convolution,SARC)法[12]等.

外加磁场时等离子体介质具有电各向异性色散特性,因此对磁化等离子体问题,需要将上述算法推广到各向异性色散介质情况.1992年Hunsberger等[13]将RC法推广用于一维磁化等离子体情形.1994年Young[14]将直接积分(direct integration,DI)法推广到磁化等离子体情形.2004年刘少斌等[15-17]先后将JEC法、PLJERC法、ADE法推广到磁化等离子体情形并计算了磁化等离子体层的反透射.2007年杨利霞等[18]将RC法推广用于一维磁化等离子体情形.

SARC算法是一种在数字信号处理(digital signal process,DSP)技术中被广泛应用、建立在对输入信号的线性插值理论基础上的快速递归卷积算法,具有低复杂性、绝对稳定和良好的精度等优点,不仅适用于稳定系统,而且还适用于渐进稳定系统和非均匀网格情况的卷积递归计算[19,20].2009年张玉强和葛德彪[12]将SARC算法应用于处理各向同性色散介质.本文根据磁化等离子体介质电磁特性,将SARC算法推广应用于磁化等离子体的FDTD分析.首先利用坐标系转换矩阵给出实验室系中磁化等离子体介质的频域极化率张量,再采用部分分式展开方法通过傅里叶逆变换得到极化率张量的时域指数函数形式,最后在对电场强度采用线性插值近似基础上应用SARC算法,给出适用于处理任意外磁场方向情形下磁化等离子体目标电磁散射的SARC-FDTD计算方法,并计算了非磁化和磁化等离子体球的后向RCS,与SO法和RC方法的结果符合得很好.数值结果表明,该方法是正确有效的.文中时谐因子取exp(jωt).

2 实验室系中磁化等离子体的频域极化率张量

磁化等离子体属于电各向异性色散介质,其频域电本构关系为

其中εr(ω)是磁化等离子体相对介电系数张量的频域形式：

各向异性介质的本构参数与所选取的坐标系有关.磁化等离子体的极化率张量在外磁场坐标系(设为x′y′z′系)中有简单的表达式,而电磁测量往往在实验室坐标系(设为xyz系)下进行.下面根据外磁场系和实验室系的转换矩阵以及外磁场系中磁化等离子体相对介电系数张量,得到实验室系中极化率张量的表达式.

建立外磁场直角坐标系：x′y′z′系,并令外磁场B0方向为z′轴正向,即轴正向单位矢,B0是B0的大小.设外磁场B0在实验室直角坐标系(xyz系)中的方向角为θt,φt,如图1所示.

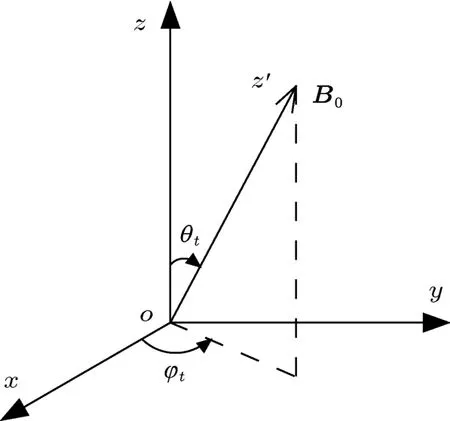
图 1 x′y′z′系和 xyz系

3 实验室系中极化率张量的时域指数函数形式

由上可知,χ(ω)各个元素χαβ(ω)可写成 jω的有理分式的真分式,可采用部分分式展开法展开为部分分式进行傅里叶逆变换.令

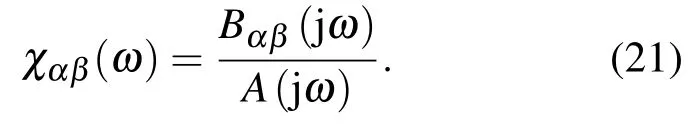
由 (14),(19)式可知χαβ(ω)的分母A(jω)有 4个单根,即A(jω)可写为

4 磁化等离子体SARC-FDTD方法

最后可以将磁化等离子体的SARC-FDTD步进计算步骤总结如下：

1)由E→H,用(49)式计算;2)由E→ψ,用(45)式计算;3)由ψ,H→E,用(51)式计算;4)回到步骤1).

5 算例验证及数值结果

图2 等离子体球的后向RCS

当外加磁场平行于z轴时,设等离子体电子回旋频率为ωce=3.0×1011rad/s.计算得到该磁化等离子体球的同极化以及交叉极化后向RCS,分别在图3(a),(b)中用实线表示,作为比较图3中同时给出RC-FDTD方法的结果[18](如图3中圆圈所示),两者符合得非常好.由于本文方法适用于处理任意磁化方向的等离子体目标,因此同时计算了外磁场沿x轴正向时该等离子体球的后向RCS(如图3中五角星所示).

图3 磁化等离子体球的后向RCS (a)同极化;(b)交叉极化

6 结论

将DSP技术中被广泛应用的SARC方法应用于磁化等离子体介质的FDTD分析,首先利用坐标系转换矩阵给出实验室系中磁化等离子体介质的频域极化率张量,再采用部分分式展开方法通过傅里叶逆变换得到极化率张量的时域指数函数形式,最后在对电场强度采用线性插值近似基础上应用SARC算法,给出适用于处理任意外磁场方向情形下磁化等离子体目标电磁散射的SARC-FDTD计算方法,并采用该方法计算了非磁化和磁化等离子体球的后向RCS,与SO法和RC方法的结果符合得很好.数值结果表明,该方法是正确有效的.

[1]Luebbers R J,Hunsberger F,Kunz K S 1991IEEE Trans.Antennas Propagat.39 29

[2]Kelley D F,Lubbers R J 1996IEEE Trans.Antennas Propagat.44 792

[3]Chen Q,Katsurai M,Aoyagi P H 1998IEEE Trans.Antennas Propagat.46 1739

[4]Liu S B,Mo J J,Yuan N C 2004Acta Phys.Sin.53 778(in Chinese)[刘少斌,莫锦军,袁乃昌2004物理学报53 778]

[5]Xu L J,Yuan N C 2005IEEE Microw.Wireless Compon.Lett.15 277

[6]Nickisch L J,Franke P M 1992IEEE Antennas Propagat.Mag.34 33

[7]Takayama Y,Klaus W 1994IEEE Microw.Wireless Compon.Lett.12 102

[8]Sullivan D M 1992IEEE Trans.Antennas Propagat.40 1223

[9]Sullivan D M 1995IEEE Trans.Antennas Propagat.43 676

[10]Sullivan D M 1996IEEE Trans.Antennas Propagat.44 28

[11]Ge D B,Wu Y L,Zhu X Q 2003Chin.J.Radio Sci.18 359(in Chinese)[葛德彪,吴跃丽,朱湘琴2003电波科学学报18 359]

[12]Zhang Y Q,Ge D B 2009Acta Phys.Sin.58 4573(in Chinese)[张玉强,葛德彪2009物理学报58 4573]

[13]Hunsberger F,Lubbers R J,Kunz K S 1992IEEE Trans.Antennas Propagat.40 1489

[14]Young L J 1994Radio Sci.29 1513

[15]Liu S B,Mo J J,Yuan N C 2004Acta Phys.Sin.53 783(in Chinese)[刘少斌,莫锦军,袁乃昌2004物理学报53 783]

[16]Liu S B,Mo J J,Yuan N C 2004IEEE Microw.Wireless Compon.Lett.14 222

[17]Liu S B,Mo J J,Yuan N C 2004Acta Phys.Sin.53 2233(in Chinese)[刘少斌,莫锦军,袁乃昌2004物理学报53 2233]

[18]Yang L X,Ge D B,Wei B 2007Acta Phys.Sin.56 4509(in Chinese)[杨利霞,葛德彪,魏兵2007物理学报56 4509]

[19]Janke W,Blakiewicz G 1995IEE Proc.Circuits Dev.Syst.142 125

[20]Pietrenko W,Janke W,Kazimierczuk M K 2001IEEE Trans.Circuits Syst.48 1246

[21]Ge D B,Yan Y B 2011Finite-Difference Time-Domain Method for Electromagnetic Waves(3th Ed.)(Xi’an：Xidian University Press)p259(in Chinese)[葛德彪,闫玉波2005电磁波时域有限差分法(第三版)(西安：西安电子科技大学出版社)第259页]

[22]BiDX1985Electromagnetic Field Theory(Beijing：Publishing House of Electronics Industry)p434(in Chinese)[毕德显1985电磁场理论(北京：电子工业出版社)第434页]

[23]Kong J A 2002Electromagnetic Wave Theory(Beijing：Higher Education Press)p333