成灌快铁高架桥梁区段噪声测试
2013-02-24李小珍尹航吴金峰张迅李亚东
李小珍,尹航,吴金峰,张迅,李亚东
(西南交通大学土木工程学院桥梁系,成都 610031)
轨道交通在解决城市的交通问题,带来快捷、方便交通的同时,也产生了噪声等问题。轨道交通的噪声由集电系统噪声、空气动力噪声、轮轨噪声、桥梁结构噪声组成(图1)。
当列车通过高架结构时,振动能量由轨道结构传到桥面和其余构件,激发其共同振动,形成结构噪声的声源。振动较大时,振动能量通过桥梁墩台传递给周围建筑,引起“二次辐射”[1]。目前,对于桥梁结构噪声的理论分析以统计能量法与边界元法为主[2―5],对高速/快速铁路高架桥梁的噪声试验研究较少[6]。
成灌快铁正线全长67 km,桥隧比高达87%,高架桥段的噪声问题比较突出。结合成灌快铁高架桥梁噪声试验,对实测结果进行分析,并运用声学原理建立简化噪声预测模型,较准确地预测了高架桥梁附近的声场分布情况。本文的研究对快速铁路高架桥梁的噪声传播规律及噪声控制具有一定的参考意义。

图1.高速铁路噪声组成示意图Fig.1 High-speed railway noise sources
1 现场试验概况
1.1 测试仪器
本试验采用丹麦B&K公司的PULSE Labshop测量系统平台,麦克风为MPA 231自由场型传声器,传声器在测量前采用标准的声级校准器进行校准,所有测试用传感器满足IEC 651(1979)以及IEC60804(1985)的要求。
1.2 现场情况
根据背景噪声、声学环境、测试安全的三方面要求选择测试工点。低背景噪声是有效测试的基本要求,而声学环境是尽量使问题简化的必要条件,所有的一切都应建立在安全的基础上。
选定的工点为郫县高架特大桥都江堰端台尾附近。工点远离公路、居民生活区、厂房等,周围环境不存在各种无规律的交通噪声、居民生活噪声或机器设备噪声等,不会对测试数据的有效性造成干扰。同时,测试工点周围视野开阔,远离屏障或反射区,气压、温度和风力变化影响小(如图2)。

图2 测试现场Fig.2 Test in-site
1.3 测点分布
工点处为32 m双线混凝土简支箱梁,梁高2.354 m,宽11.4 m,横坡2.00%,腹板为圆弧形。设计速度200 km/h,左右两线相距4.4 m。经现场实测,双线简支箱梁跨中底板底面至地面的平均距离为3.7 m。
图3给出了双线箱梁跨中横截面的测点布置详图,从垂直于左线中心线开始,间隔7.5 m、16.25 m、25 m、50 m分别布置了4列高9 m的测点阵。B1测点位于箱梁底板附近(距底板约30 cm),B2测点位于桥梁遮板上边缘(遮板距梁面的高度约1.65 m)。
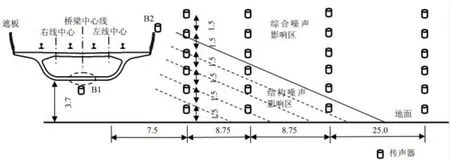
图3.麦克风布置示意图Fig.3 Arrangement of microphones
2 试验结果分析
B 2测点实测噪声受到多种噪声的综合影响,最能够反映高架结构辐射的综合噪声。图4―图5给出了列车以时速198 km/h在右线运行时(工况DC198),各典型时刻的声压级频谱曲线。图4采用线性计权声压级Lp,图5采用A计权声压级LA。工况编号中,“DC”指列车在右线运行(远轨),“CD”指列车在左线运行(近轨),数字“198”指车速为198 km/h。典型时刻是指列车通过测试断面的时间内(以车速198 km/h为例,时长约3.7 s),取其中声级最大且较平稳时间段内,间隔为0.5 s的测量时刻。
对比图4与图5可以发现:当分别采用线性计权和A计权时,B 2测点的噪声级相差将近10 dB左右,这说明该点的噪声存在较强的低频成分。由于此处的噪声成分较为复杂,包含了前述各噪声源,因此暂不能确定此低频成分是否为桥梁结构噪声引起。
图6给出了箱梁底板附近测点B 1在各典型时刻的线性声级频谱曲线,列车运行工况同前。
由于B 1测点位于箱梁底板附近,受到箱梁结构本身的遮挡作用,所测噪声主要为桥梁结构噪声。从图5可以看出,高架桥梁结构噪声含有较强的低频成分,且主要集中在200 Hz以下频段,这一规律不随列车在桥梁上的运行轨道(左线或右线)、车速、位置变化而改变(由于篇幅限制,本文未给出其它工况下的频谱曲线)。由此,可以推测图3中综合噪声的较强低频成分主要由桥梁结构噪声引起。

图4 B 2点在各典型时刻的线性声级频谱曲线Fig.4Lpof microphone B 2 at different time

图5 B 2点在各典型时刻的A声级频谱曲线Fig.5LAof microphone B2 at different time
进一步分析图4可知:B 2测点实测噪声存在两个明显的噪声峰值频段,一个处于较低的频段,在100 Hz以下;另一个处在较高的频段,在中心频率为800 Hz附近,二者的峰值差在5 dB左右,说明二者对合成声压级均有较大的贡献。由此可知,对于高架结构的噪声分析宜采用线性计权的方式,这样能够较完整地考虑包括桥梁结构这种以低频为主的噪声的影响。
图7给出了各测试工况下,B 2测点的实测最大噪声级。
分析图7可知:列车在近轨运行时,B 2测点处的噪声级要比远轨大;车速越高,噪声级越大,但也有例外,如DC 154的噪声大于DC 158,分析桥梁在两个工况下的振动加速度可知,DC 154工况下桥梁的振动更大,导致噪声也更大。需要指出的是:由于实测均为过路车,虽然均为CRH 2动车组,但每列车的运行状态可能是不一致的。

图6 B 1点在各典型时刻的线性声级频谱曲线Fig.6Lpof microphone B 1 at different time

图7 各工况下B 2点的最大声级Fig.7 The maximum sound pressure level of B 2 point in various working conditions
根据测点阵的测试数据做出的声场等效连续声级Leq分布云图如图8所示(工况DC 198),声场的范围为桥梁中心线一侧的7.5 m到50 m,距离地面高度为9 m。
图8(a)采用线性计权方式,桥梁斜上方和斜下方分别存在一个噪声“热点”区域。斜上方的噪声热点区域主要由轮轨噪声等产生,斜下方的噪声热点区域主要由桥梁结构噪声产生。
图8(b)采用A计权处理,桥梁斜下方的噪声热点区域将不再出现,而仅有桥梁斜上方的噪声“热点”区域,这是由于桥梁结构噪声的低频特性。
从图8还可以看出,距地面高度为9.0 m测点的等效声级沿横桥向的衰减速率要快,而距地面高度为1.5 m测点的等效声级沿横桥向的衰减速率要慢,说明低频噪声的衰减比较缓慢,与低频噪声的传播性质相吻合。
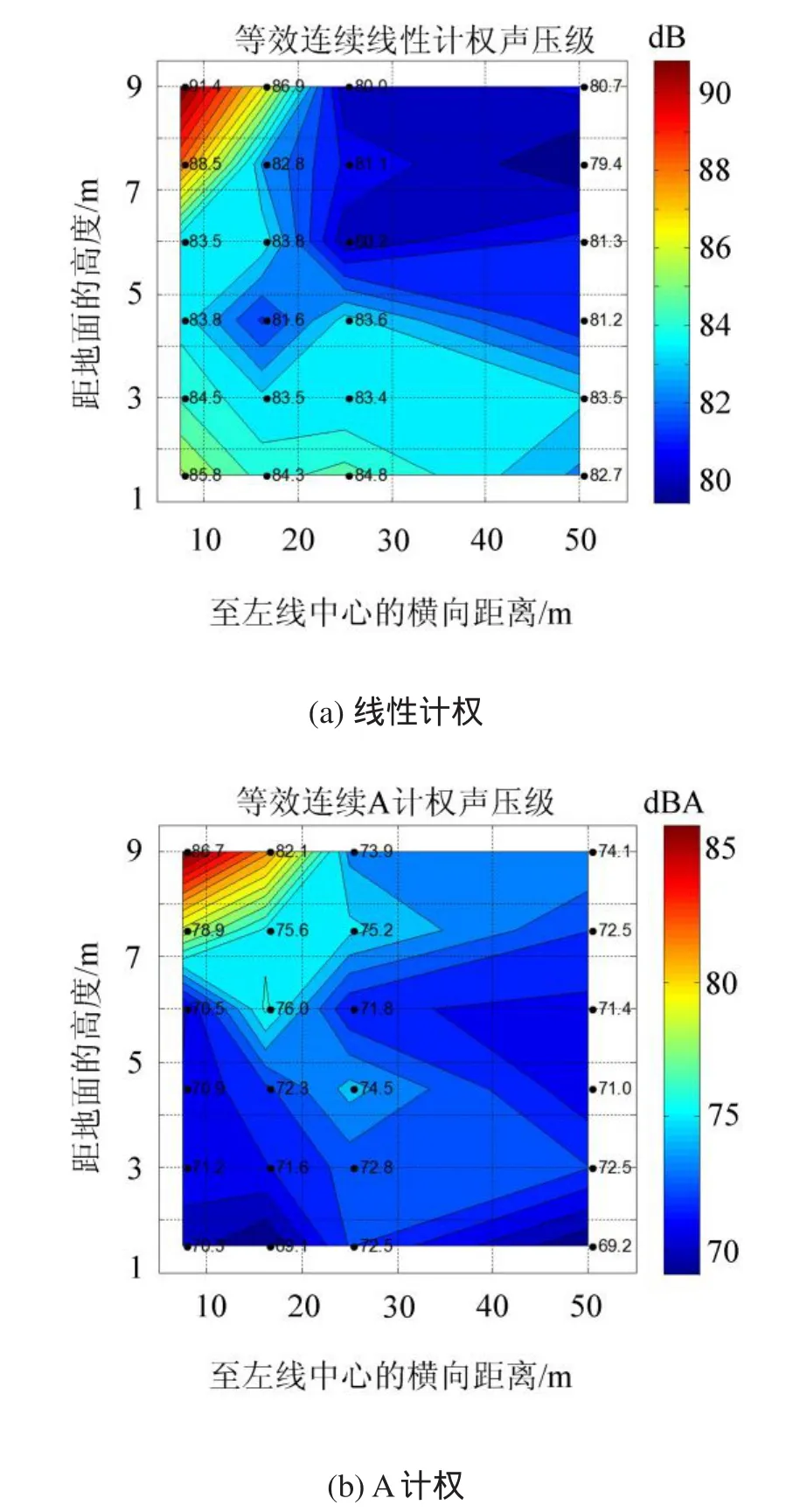
图8 梁侧综合噪声的等效连续声级分布云图Fig.8Leqdistribution around the bridge
图9给出了不同高度处,等效连续线性声压级Leq与至桥梁中心不同距离的变化规律。
从图9中可见,不同高度的声压级基本都随着水平距离的增大而减小,符合客观规律。在同一水平距离不同高度的噪声级大小则没有固定的变化趋势,这是由于不同高度处受到前述各种噪声成分的影响不同。离梁底越近的测点,越容易受桥梁结构噪声的影响;而越高离轮轨越近的测点,越容易受轮轨噪声绕射过遮板的影响。
3 噪声预测模型
本文建立的噪声预测模型的思路是:取一个噪声参考点,根据声波的叠加、发散、衰减等规律,预测不同位置处的噪声情况。
文献[6,7]给出了若干噪声源组合的简化公式
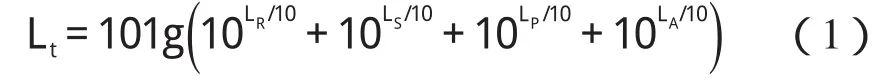
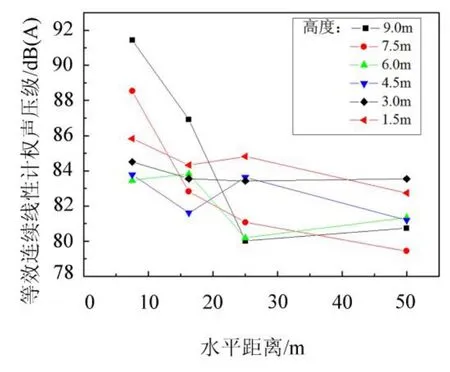
图9 不同高度处等效连续线性声压级随距离变化图Fig.9Leqat different horizontal distance and heights
式中LR、LS、LP、LA为轮轨噪声、桥梁结构噪声、集电系统噪声、空气动力噪声。
根据前面对实测结果的分析,假设各噪声源的影响分布如图2所示,即阴影内只受到桥梁结构噪声影响,阴影外还收到其它三种噪声(记为LRAP)的影响。故式(1)可改写为

声波的衰减主要是分为几何发散和空气吸收,当天气条件、温度等变化时,也会不同程度地影响声波的衰减,在该声场研究范围内,空气吸收的影响很小,可忽略不计。
此外,声波遇到障碍物的时候会发生发射,如地面、各种建筑物也会使声波的辐射发生变化。本预测模型中,运用虚声源法来模拟地面对声波的反射作用[5]。
动车组以高速(120 km/h以上)经过高架结构时,可将其看成是沿线路方向的线声源。在《环境影响评价技术导则―声环境》(HJ/T 2.4-1995)中列出了有限长线声波几何发散衰减的基本公式。设线声源长度为l0,垂直于声源的中心线上

本次试验中,线声源长度为32 m(高架桥一跨长度)。B1测点位于箱梁底板附近,受到箱梁结构本身的遮挡作用,所测噪声视为桥梁结构噪声。B2测点位于桥梁遮板上边缘,所测噪声视为其它三种噪声的组合。
以B1、B2测点为参考点,所测线性声压级为参考声压级。考虑结构噪声以及其它三种噪声的几何衰减,再进行组合来建立预测模型。以工况CD162为例,根据公式预测出的估算值与实测值的比较结果见表1。

表1 预测模型估算值与实测值对比Tab.1 The comparison of the prediction model results and measured values
为了更好地比较预测值和实测值的差异性,运用非参数检验的方法分析预测值与实测值两个独立样本的差异性。非参数检验是指在总体分布情况不明时,用来检验数据是否来自同一个总体假设的一类检验方法。表2给出了预测值与实测值的绝对值误差结果,表3给出了预测值与实测值的样本分布一致性检验结果。

表2 预测值的绝对值误差Tab.2 Descriptive data of the absolute set error
从表2可以看出,绝对值误差均值为1.54,说明预测值与实测值能够较好地符合。

表3 预测值与实测值的样本分布一致性检验Tab.3 The consistency test for the predicted and the measured values
从表3可以看出,Z
根据上述分析,图10给出了预测值与实测值的线性回归分析结果。回归方程为y=1.002x,R2=0.999 7,进一步验证了预测值与实测值两个样本的一致性,说明用了预测模型与实测数据具有相当高的拟合程度,可用于轨道交通高架桥梁的噪声预测。
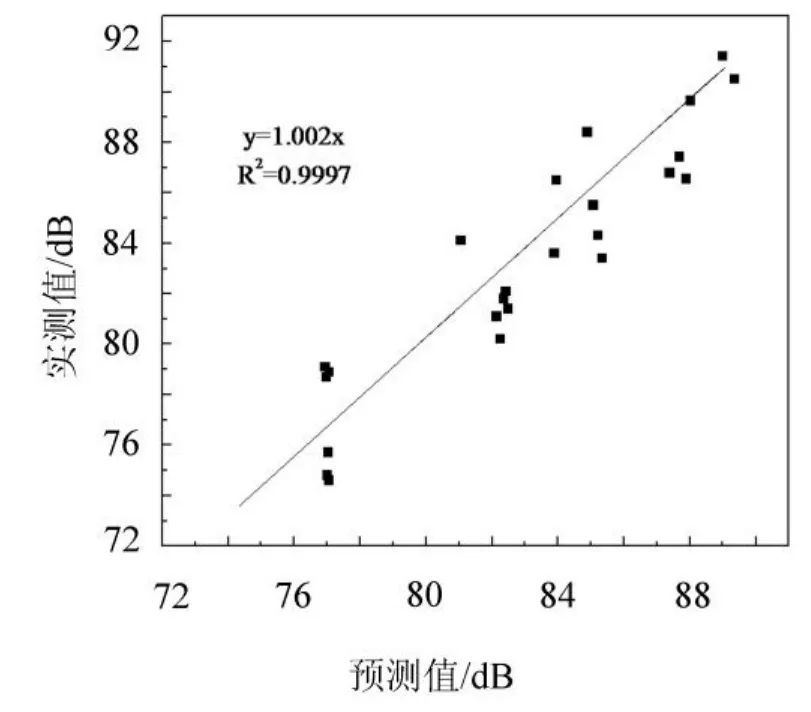
图10 预测值与实测值的线性回归分析Fig.10 Linear regression analysis for the predicted and the measured values
4 结语
1)高架桥梁辐射噪声以低频为主,对于这种噪声宜采用线性计权的方式处理。
2)高架桥梁附近的噪声具有两个明显的噪声峰值频段,一个处于较低的频段,在100 Hz以下;另一个处在较高的频段,其中心频率为800 Hz附近;
3)桥梁结构噪声主要集中在桥梁斜下方一定区域,随横向距离增加,其幅值的衰减较慢;
4)由二维声场简化预测模型得出的计算值与实测值的误差较小,非参数检验以及线性回归方法证明了该简化预测模型具有一定的精度,可用于轨道交通高架桥梁的噪声预测。
[1]Thompson D J.Railway noise and vibration-mechanisms,modeling and means of control[M].Elsevier Ltd.,2009:359.
[2]Ngai K W,Ng C F.Structure-borne noise and vibration of concrete box structure and rail viaduct[J].Journal of Sound and Vibration,2002,255(2):281-297.
[3]Bewes O G,Thompson D J,Jones C J C,et al.Calculation of noise from railway bridges and viaducts:experimental validation of a rapid calculation model[J].Journal of Sound and Vibration,2006,293(3-5):933-943.
[4]谢旭,张鹤,山下幹夫,等.桥梁振动辐射低频噪声评估方法研究[J].土木工程学报,2008(10):53-59.
[5]李小珍,张迅,李亚东.高速铁路桥梁结构噪声研究的边界元法[J].土木工程学报,2011,44(S1):95-101;185.
[6]高飞,夏禾,安宁.北京地铁5号线高架结构的辐射噪声分析与实验研究[J].中国铁道科学,2010,31(5):134-139.
[7]焦大化.日本高速铁路噪声预测方法[J].铁道劳动安全卫生与环保,2007,34(1):35-38.
