一种EMD阈值寻优降噪方法

黄建招，谢建，李良，许建国

（第二炮兵工程大学兵器发射理论与技术国家重点学科实验室，西安 710025）

经验模态分解方法（Empiricalmode decompositi on,EMD）是Huang等[1]提出的一种用于非线性和非平稳数据分析的新方法，它能使任何复杂数据集合按照从高频到低频的顺序，分解为有限的本征模态函数（Intrinsic Mode Function,IMF）。经验模态分解方法是一种数据自驱动处理方法，克服了小波分解需选取小波基的不足，在地震波分析、气候数据分析和机械信号处理方面得到了广泛的应用，并取得了良好效果。Flandrin等[2]通过对EMD的滤波特性进行研究，得出EMD具有和小波相类似的二进滤波器特性。因此，利用EMD对混杂有随机噪声的信号进行分解，经EMD分解后的高频IMF分量通常情况下为噪声，将高频噪声剔除，保留剩余IMF并求和，从而获得降噪信号。这就是EMD滤波的基本原理[2,3]。基于上述原理，EMD降噪方法大致可分为：（1）直接提取法。文献[4]在EMD分解的基础上，提出一种以相邻均方根误差最小为标准选取IMF进行信号降噪的方法，并与平均、中值和小波滤波三种方法进行了对比。文献[5]和[6]在Wu等对白噪声EMD分解特性研究[7]的基础上，提出以能量密度和平均周期乘积的“跳变点”作为降噪IMF选取的分界点，但并未给出“跳变点”的定量指标。（2）阈值处理法。文献[8]针对语音信号降噪，提出一种对EMD分解得到的所有IMF分量进行硬阈值降噪（提出新阈值）处理的新方法，并将该方法与小波同时应用到语音信号的降噪对比试验，取得了优于小波的降噪效果。文献[9]论述了一种EMD软阈值降噪方法，方法将EMD分解和小波阈值去噪相结合，对所有IMF分量进行软阈值处理，从而实现信号的降噪；文献[10]提出将两个相邻过零点间包含一个波峰或波谷的信号称为模态单元，以模态振幅决定该整个模态单元的取舍。由于这种方法以一个振荡单元代替单个数据点，所以极易由于局部强噪声造成模态振幅超过阈值，对应的整个模态单元被滤除，从而造成模态单元中的有用信号大量丢失。针对直接提取法存在的不足和阈值降噪的优点，本文提出一种EMD阈值寻优降噪方法，方法首先按照基于能量角度设计的算法确定“跳变点”位置，从而实现IMF选取，然后通过比较选取IMF和被剔除IMF分量的能量，对符合算法要求的部分已选取IMF进行阈值处理，最后将选取的IMF求和得到降噪信号。与其它方法进行降噪对比试验，证明本方法能够在不同噪声强度下自适应寻找最佳IMF分量进行合成和降噪。

1 相关理论概述

1.1 经验模态分解方法

经验模态分解方法依据信号自身特点通过“筛选”过程将信号分解为一系列本征模态函数IMF。根据Huang的定义，每个IMF需要满足两个条件：（1）在整个数据段内，极值点的个数和零交叉点的个数必须相等或相差最多不能超过一个；（2）在任何一点，由局部极大点形成的包络线和由局部极小值点形成的包络线的均值为零。

经验模态分解方法的筛选过程如下

（1）首先求取信号x(t)的极大值点和极小值点，用三次样条曲线插值分别求取所有极大值点和极小值点形成的上包络线和下包络线。记信号x(t)上下包络线的均值为m1(t)，信号x(t)与均值m1(t)的差记为h1(t)，则h1(t)=x(t)-m1(t)；

（2）考察h1(t)是否满足IMF的约束条件，如果满足则到下一步，否则将h1(t)作为新的x(t)重复上一步，直到h1k(t)满足IMF的约束条件，从而求得从原始信号中筛选出的第一个IMF：c1(t)=h1k(t)；

（3）将c1(t)从x(t)中分离出来，得到差值信号r1(t)=x(t)-c1(t)，把r1(t)作为新信号重复上述筛选步骤，直到第n阶的残余分量rn(t)为单调信号或者只存在一个极值点（总体停止条件）为止；

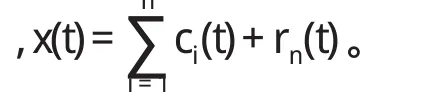
1.2 IMF的选取

文献[7]通过研究白噪声的统计特性总结出如下结论：所有的IMF均服从正态分布；各个IMF的傅立叶谱是一致的，在半对数尺度坐标下覆盖同一区域；同时还得出IMF的能量密度和其对应的平均周期的乘积是一个常数。参考文献[5]和[6]，定义能量密度En和平均周期如式（1）、（2）所示。

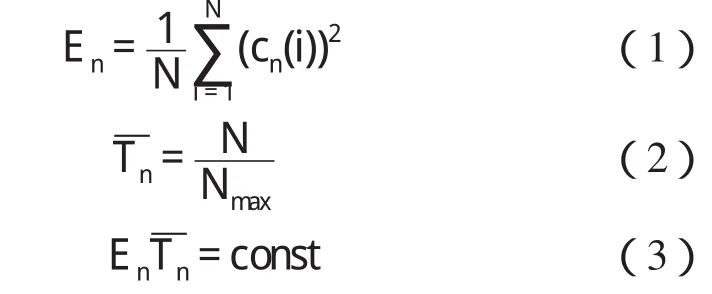
式（1）En表示第n个IMF分量cn的能量密度，N为数据长度；式（2）表示第n个IMF分量cn的平均周期，Nmax表示cn中极大值的数目。式（3）表示能量密度和其对应的平均周期的乘积是一个常数。对于正态分布的白噪声序列可假设（3）式中的常数为1。

原始信号经EMD分解得到各个IMF，按照式（1）―（3）求出En，和Enn。由于经EMD分解后的高频IMF分量通常情况下为噪声，且白噪声的En的为一常量，所以En曲线的第一个“跳变点”处的分解级数即为有用信号的IMF分量，剔除“跳变点”以前的IMF分量，将剩余的IMF组合即得降噪后的信号。

2 EMD阈值寻优降噪方法

2.1 问题的提出

为了研究基于能量的IMF直接选取法的特性，利用模拟信号x(t)进行研究分析，模拟信号x(t)由周期为1 200 s、600 s和50 s的三种正弦信号叠加组成，采样间隔为1 s，采样点数取为4 000点。为模拟信号x(t)添加不同强度的高斯白噪声。噪声均方差从0.5开始，以0.5等差递增到4。运用1.2节论述的IMF选取方法，计算不同噪声强度条件下分解所得IMF的En。仿真试验结果表明，不同噪声强度下EMD分解获得的IMF数量不同，噪声强度越大，IMF数量越多。同时，由于Matlab产生白噪声的随机性，所以每次运行得到的结果会存在差异，但这种随机性并不影响白噪声的统计特性。表1给出了100次试验中前8个IMF分量En-Tn的平均值。

2.2 阈值寻优降噪方法

在基于能量进行IMF分量选取降噪和大量实验分析的基础上，针对2.1节论述的问题，提出一种EMD阈值寻优降噪方法。方法的具体步骤如下：

（1）对待降噪信号进行EMD分解，获得IMF分量；

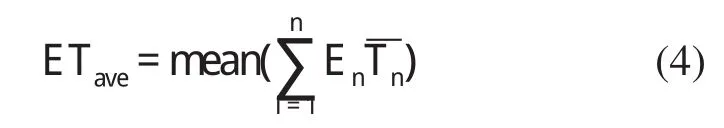
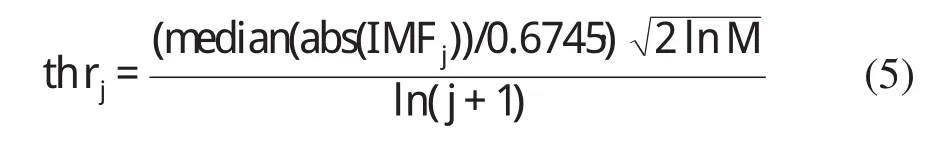
式中M代表信号的数据长度，j代表IMF分量的序数，即第j个IMF分量。

（6）经过步骤（1）―（5）后，对第n+1个IMF分量以后的所有IMF分量及趋势项求和，得到降噪信号。

3 降噪试验

为了验证本文提出的EMD阈值降噪方法的可行性和有效性，对两种仿真信号进行降噪试验，并与文献[4]、文献[6]和文献[8]三种降噪方法进行了对比。鉴于文献[6]中未提供“跳变点”的具体选取方法，在编程实现时采用本文2.2节论述的方法确定“跳变点”。降噪效果以信噪比SNR、均方根误差

RMSE和相关系数R作为评价指标。

3.1 试验一

模拟信号x(t)由周期为1 200 s和600 s，振幅为1的两种正弦信号叠加组成，数据采样间隔为1 s，采样点数取为4 000点。对模拟信号添加不同噪声方差的高斯白噪声，强度从0.5开始，以等差0.5递增至4。因篇幅有限，在此只给出噪声强度分别为1.5和3时运用4种不同方法得到的降噪信号，如图1和图2所示。表2给出了4种不同方法对应的不同噪声强度下降噪的信噪比SNR、均方根误差RMSE和相关系数R。

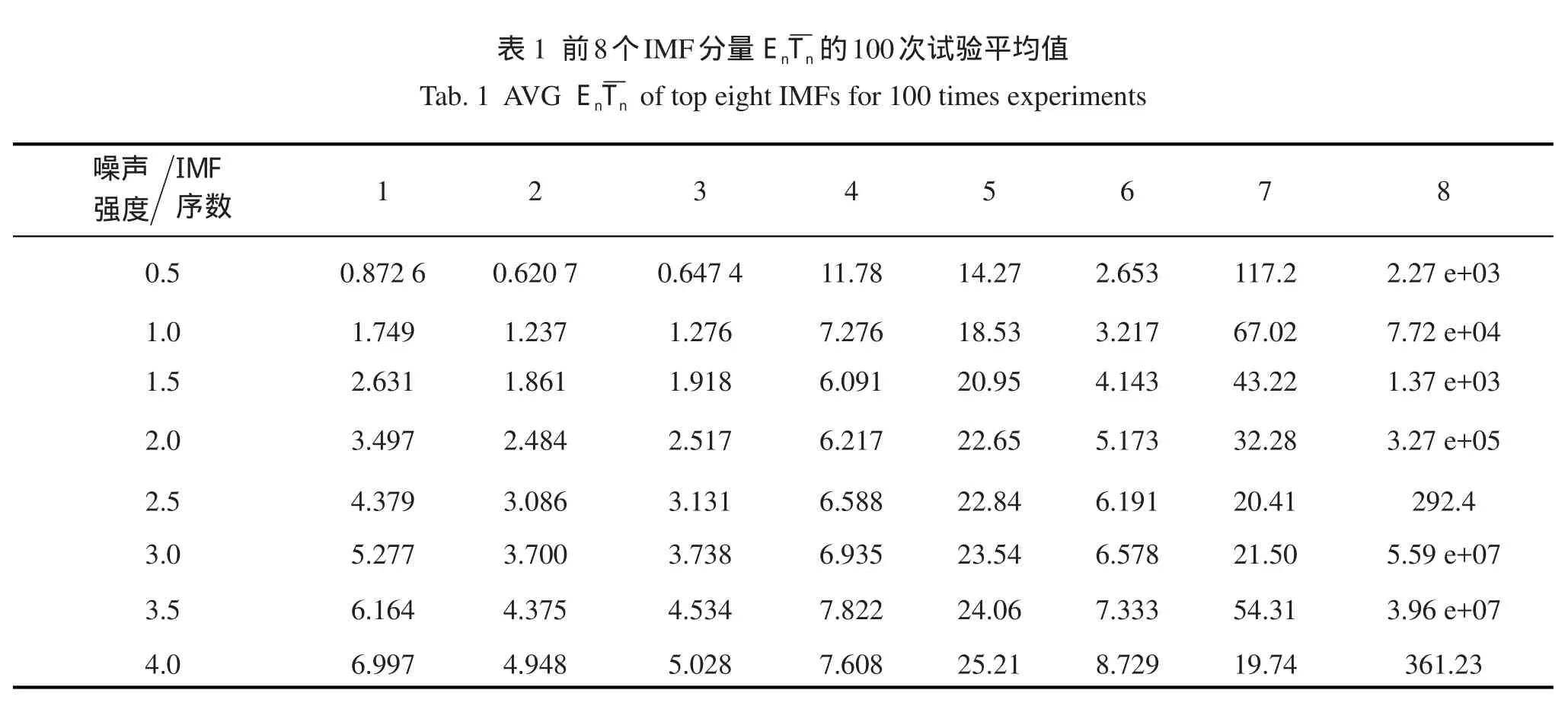
表1前8个IMF分量的100次试验平均值Tab.1 AVGof top eight IMFs for 100 times experiments噪声强度IM F序数0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 1 0.872 6 1.749 2.631 3.497 4.379 5.277 6.164 6.997 2 0.620 7 1.237 1.861 2.484 3.086 3.700 4.375 4.948 3 0.647 4 1.276 1.918 2.517 3.131 3.738 4.534 5.028 4 11.78 7.276 6.091 6.217 6.588 6.935 7.822 7.608 5 14.27 18.53 20.95 22.65 22.84 23.54 24.06 25.21 6 2.653 3.217 4.143 5.173 6.191 6.578 7.333 8.729 7 117.2 67.02 43.22 32.28 20.41 21.50 54.31 19.74 8 2.27 e+03 7.72 e+04 1.37 e+03 3.27 e+05 292.4 5.59 e+07 3.96 e+07 361.23

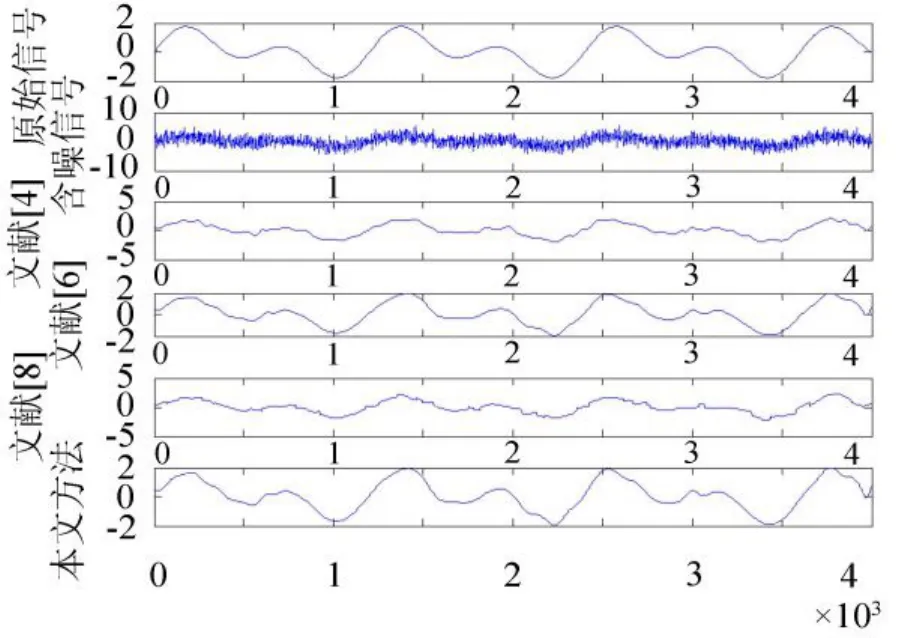
图1 噪声强度为1.5时四种方法降噪效果Fig.1 Four methods de-noising effectunder noise density 1.5

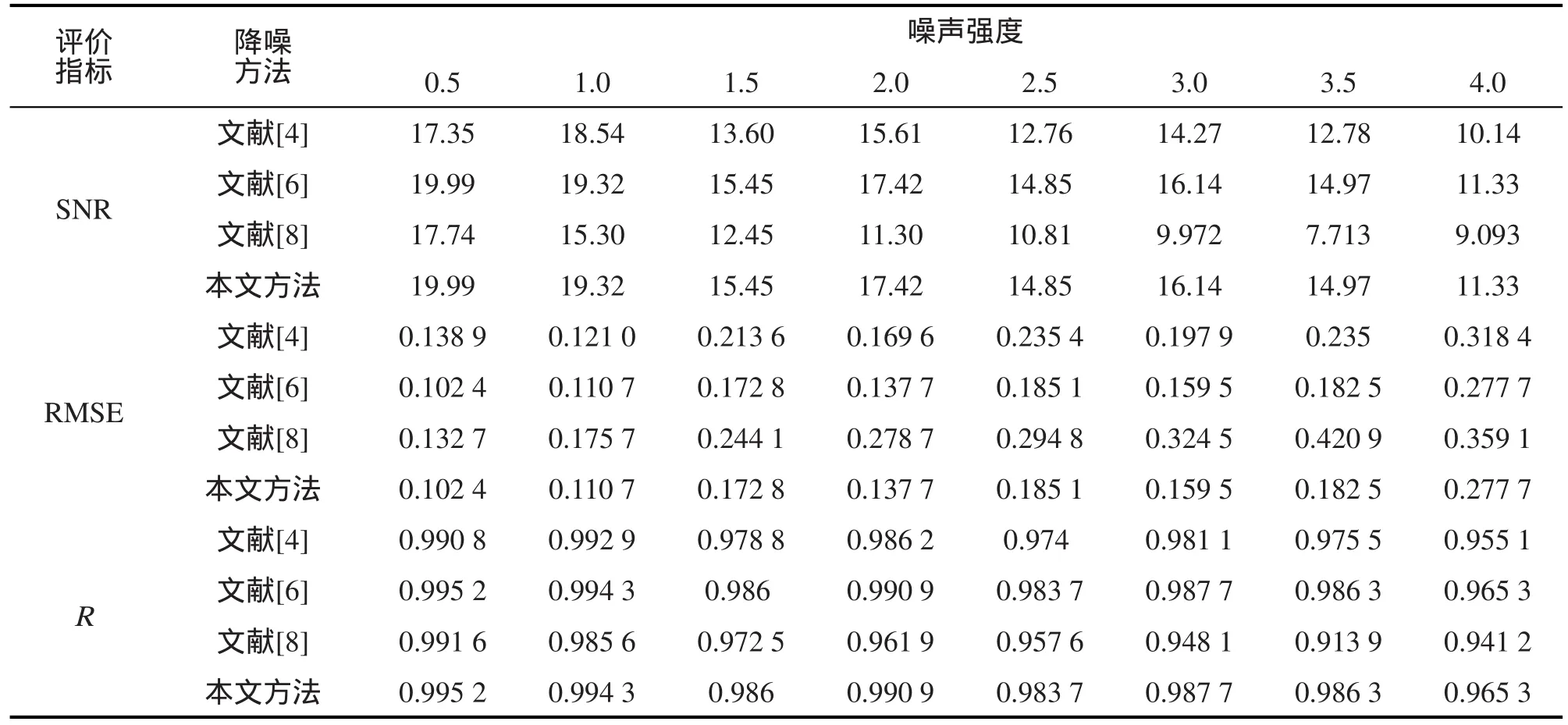
表2 四种降噪方法在不同噪声强度下的评价指标Tab.2 Evaluation indexes of four methods under different noise density

3.2 试验二

模拟信号x(t)采用2.1节论述的信号，与试验一的模拟信号相比，增加了高频分量。噪声强度依然从0.5开始，以等差0.5递增至4。图3和图4给出了噪声强度分别为1.5和3时运用4种不同方法得到的降噪信号。表3给出了4种不同方法对应的不同噪声强度下降噪的信噪比SNR、均方根误差RMSE和相关系数R。

从表3可以看出，本文提出的方法在不同噪声强度下的三种评价指标优于其他三种方法。与试验一相比，试验二中本文方法要比文献[6]的方法降噪效果明显，说明2.2节中的“奇异”IMF判定标准和软阈值降噪发挥了作用，验证了方法的有效性。

4 结语

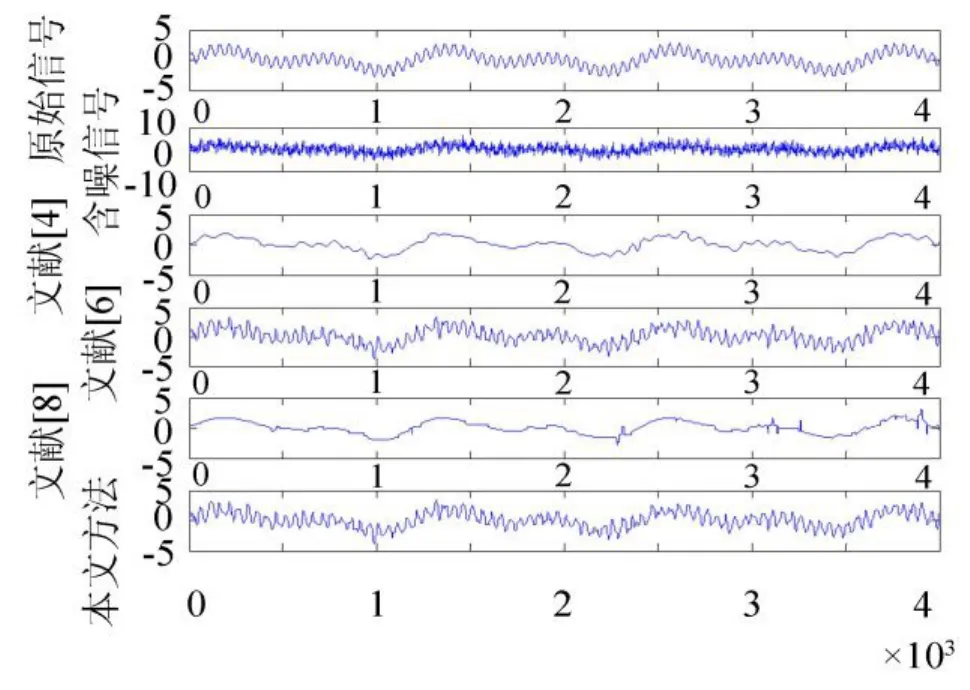
图3 噪声强度为1.5时四种方法降噪效果Fig.3 Four methods de-noising effect under noise density 1.5

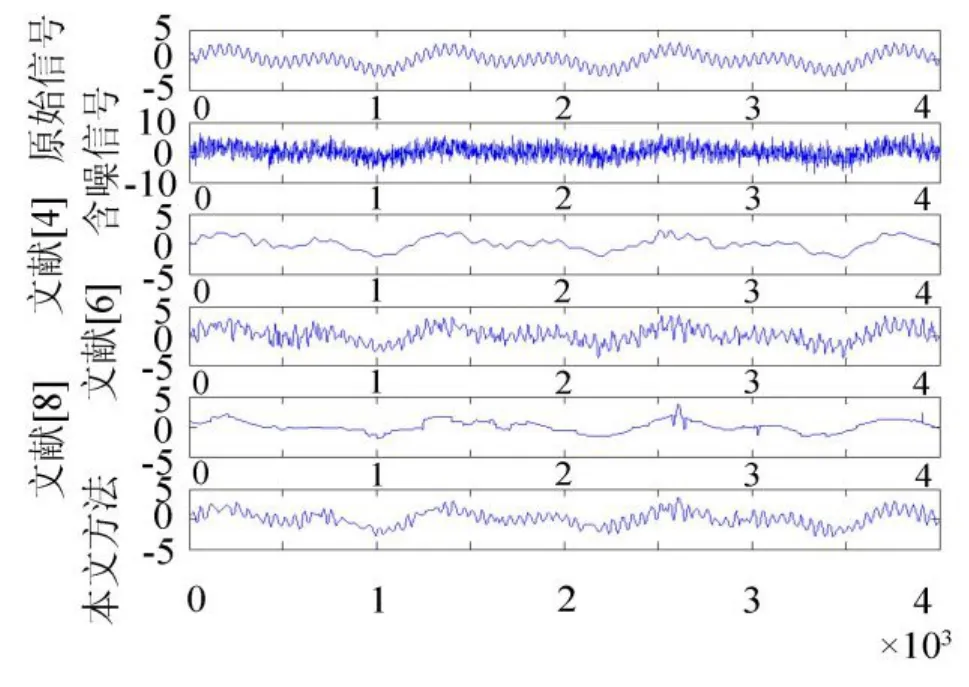
图4 噪声强度为3.0时四种方法降噪效果Fig.4 Four methods de-noising effectunder noise density 3.0

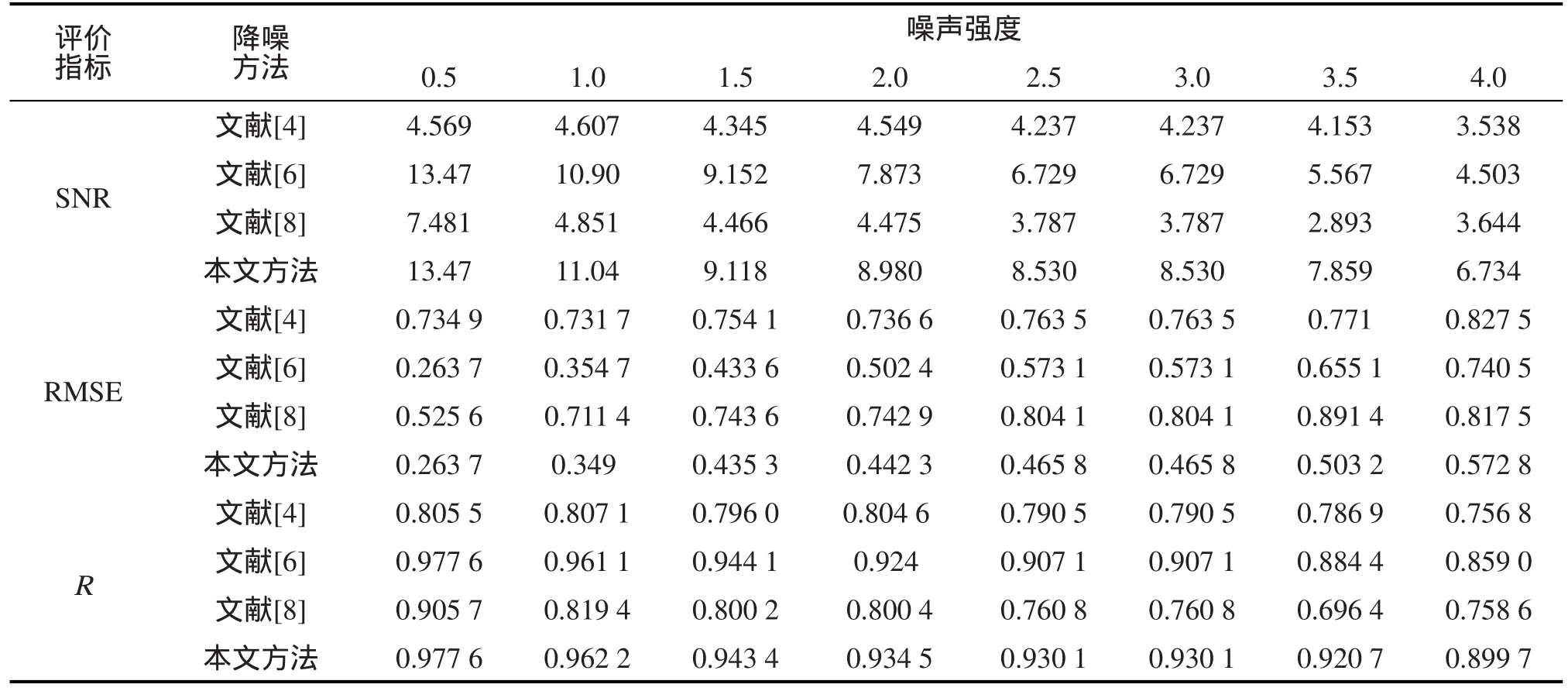
表3 四种降噪方法在不同噪声强度下的评价指标Tab.3 Evaluation indexes of four methods under different noise density

[1]Huang N.E.,Shen Z.,Long S.R.,et a1.The empirical mode decomposition and the Hilbertspectrum for nonlinear and non-stationary time series analysis[J].Proc.R.Soc.Lond.A,1998，454:903-995.

[2]Flandrin P.,Rilling G.,Goncalves P.Empirical mode decomposition as a filter bank[J].IEEE Sig.Proc.Lett.，2004，11(2)：112-114.

[3]陈凯.基于经验模式分解的去噪方法[J].石油地球物理勘探，2009，44(5)：603-608.

[4]Boudraa A.O.,Cexus J.C.EMD-based signal filtering[J].IEEE Trans.Instru.Meas.，2007，56(6)：2196-2202.

[5]王翔，刘晓锋，朱正林.基于EMD的汽轮机碰摩信号消噪技术研究[J].汽轮机技术，2011，53(1)：71-73.

[6]李志全，曹平，王亚男，等.基于经验模态分解消噪的光纤光栅解调系统[J].光子学报2010，39(8)：1367-1370.

[7]Wu Z.H.,Huang N.E.A study of the characteristics of white noise using the empirical mode decomposition method[J].Proc.R.Soc.Lond.A，2004,460:1597-1611.

[8]khaldi K.Boudraa A.O.,Bouchikhi,A et al.Speech signal noisereductionbyEMD[C].ISCCSP,Malta,2008,1155-1158.

[9]Boudraa A.O.,Cexus J.C.Denoising via empirical mode decomposition[C].in Proc.IEEE ISCCSP,Marrakech,Morocco,2006,4-8.

[10]曲从善，路延镇，谭营.一种改进型经验模态分解及其在信号消噪中的应用[J].自动化学报，2010，36(1)：67-73.

[11]Donoho D L.De-noising by soft-thresholding[J].IEEE Transactions on Information Theory,1995,41(3):613-627.