抗噪声源时滞引起的尖峰噪声分析及抑制
2013-02-24姚加飞罗梦莹
姚加飞,罗梦莹
(重庆大学输配电装备及系统安全与新技术国家重点实验室,重庆 400044)
有源噪声控制(ANC,Active noise control)的原理是应用电子技术和电声器件,引入一个与初级噪声幅值大小相等而相位相反的抗噪声源,使其在一定区域内相互抵消,从而达到降低噪声的目的[1]。与无源噪声控制对低频噪声效果较差相比,有源噪声控制技术擅长于低频噪声的控制,能够很好地与无源噪声控制形成互补[2]。采用有源噪声控制技术降噪的前提是能够产生实时的抗噪声源,即与初级噪声相位完全相反的抗噪声源,在实际应用中,由于线路延时,控制动作延时、声音空间传播延时等因素存在,抗噪声源会不可避免的滞后于初级噪声。当抗噪声源出现时滞,与初级噪声不同步时,某些时候可能会产生比初级噪声更大的噪声,达不到降噪效果。为解决时滞引起的尖峰噪声问题,文献[3]利用模糊控制的方法对尖峰噪声进行了抑制,有一定的降噪效果,但其缺乏深入的理论分析。本文利用傅里叶变换理论分析出初始噪声和降噪后噪声幅值和相位的关系表达式,通过对抗噪声源时滞引起的尖峰噪声进行频谱分析进行验证,并根据幅值和相位关系式对降噪后噪声进行直接控制,达到较好的降噪效果。
1 抗噪声源时滞
噪声是随机的,其能量、出现时间、地点都是不确定的,为简化研究模型,本文只针对时间延迟引起的尖峰噪声进行研究。初级噪声通过控制线路和控制器处理后,输出的抗噪声源存在一定的延时,与初级噪声并不是完全的相位相反,初级噪声与抗噪声源叠加后,某些情况下可能不仅达不到降噪的效果,还可能会出现比初级噪声更大的尖峰噪声。如图1所示,理想正弦信号延时半个周期,原信号与反向延时信号重合,两者叠加后的信号幅值最大,是原信号幅值的两倍,实际噪声一般不是单一频率的,但可看做是单频率噪声的叠加,所以可以用图1表明抗噪声源时滞能引起的糟糕的反效果。有源噪声控制系统实际应用中,出现如图1所示控制后噪声比原噪声还大的情况是不被允许的,需对其进行进一步分析,找出有效的方法来解决尖峰噪声的问题。
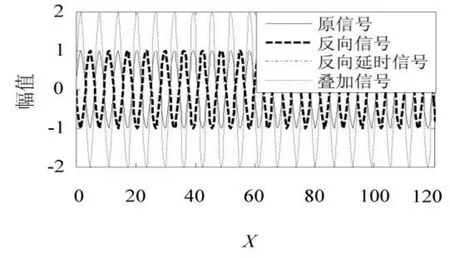
图1 模拟抗噪声源时滞效果图Fig.1 Simulation of time delay of the anti-noise source
2 尖峰噪声的理论分析
延时叠加信号可表示为
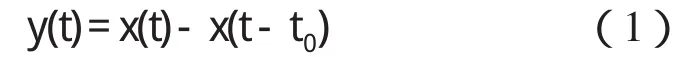
其中y(t)为延时叠加信号;x(t)为原信号;x(t-t0)为延时信号,延时时间为t0;
对式(1)进行傅里叶变换可得出[4]

通过傅里叶变换可直接得出叠加后信号幅值与相位的变化情况,式(3)表示幅值变化情况,式(4)为相位变化情况。通过仿真分析验证变化公式是否适用于实际有源噪声控制过程。
3 尖峰噪声的仿真分析
采集实际噪声,模拟有源噪声控制过程对实际噪声进行反向延时叠加,对不同延时下叠加噪声信号进行进一步分析比较,研究延时对降噪效果的影响。
实验仿真以采集到的48 s的音频信号(如图2所示)做为原信号,输入到Matlab中。将音频信号输入到电脑中所采用的是采样频率fs为44.1 kHz的声卡,因此仿真分析中采用的采样频率fs也为44.1 kHz。将其直接反向得到的信号作为理想的抗噪声源,在反向信号中加入一段时间的延时作为有时滞的抗噪声源,将原信号与有延时反向信号的叠加模拟实际有源噪声控制的效果。
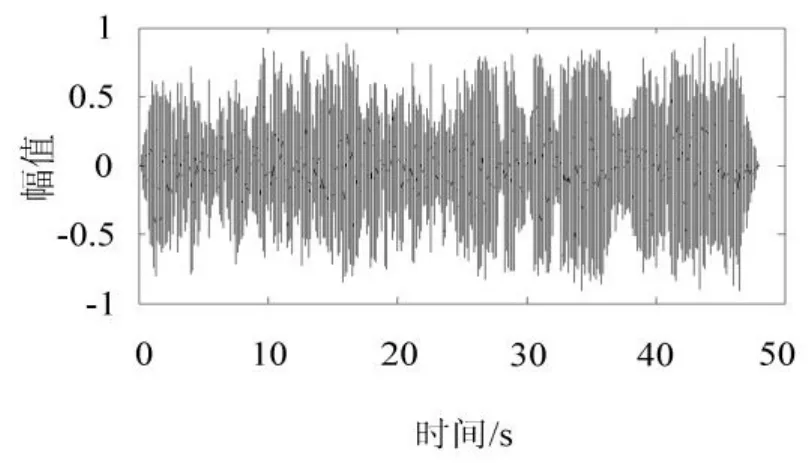
图2 原始信号波形Fig.2 Waveform of primary signal
3.1 频谱分析
频谱分析能获得信号中的能量与频率的关系。频谱分析的概念是将周期波分解为一系列谱波,进行频谱分析可以了解周期信号中的频谱结构,以频谱为横坐标,以声压级或声功率级为纵坐标绘制噪声测试结果,可以清楚的反映出噪声的频率成分和性质[5]。由噪声频谱,能清晰地表示出一定频率范围内,信号幅值和声压级的分布情况。
对采集到的原信号进行频谱分析,得出频谱图(如图3(a)所示),频谱分析时采样频率为44.1 kHz,完整频谱图应为以22.05 kHz为中心的对图形,图3只截取了其中10 kHz以下部分。从频谱图中可看出,原信号的频谱大多集中在2 000 Hz以下,低频成份较大,高频部分基本可以忽略不记。有源噪声控制是一种有效的低频消声方法,因此选择该信号来进行仿真分析是可行的。
为模拟实际有源噪声控制系统的应用,输出的与初始噪声幅值大小相等、相位相反的抗噪声源与初始噪声相比,有一定的滞后,本文将原信号波形反向,并延时不同时间,与原信号进行叠加,观察叠加后信号与原信号的变化情况,分析其降噪效果。以延时时间0.001 s为例,来分析叠加后信号与原信号的变化,叠加后信号频谱图如3(b)所示。
比较图3(a)、(b)会发现,当延时时间为0.001 s时,低频中某些频率下的叠加信号很明显比原信号
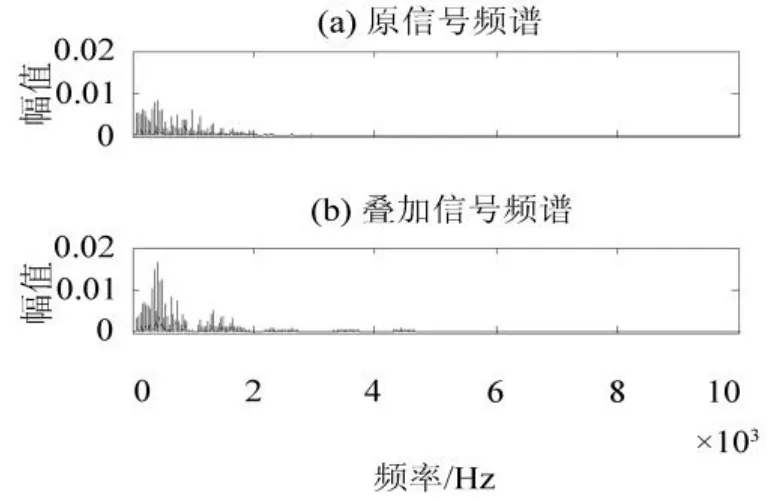
图3 原信号和叠加信号频谱图Fig.3 Spectrum of primary signal and superposed signal
大,不仅达不到有源噪声控制系统降噪的效果,还产生了更大的噪声,这就是由于时滞而引起的尖峰噪声。
3.2 幅值变化分析
为了分析原信号与叠加信号频谱的变化情况,两者进行相除比较,得出叠加后信号与原信号在不同频率下幅值的变化情况,当延时时间为0.001 s时,绘制图形如图4所示。从中可看出,叠加信号与原信号的比值大致遵循周期正弦分布的规律。图4波形周期为1 000 Hz,最大幅值为2,虽然在大于10 kHz的高频部分出现一定的干扰,但有源噪声控制研究的主要是低频噪声信号,对于高频出现的问题可以忽略不记。
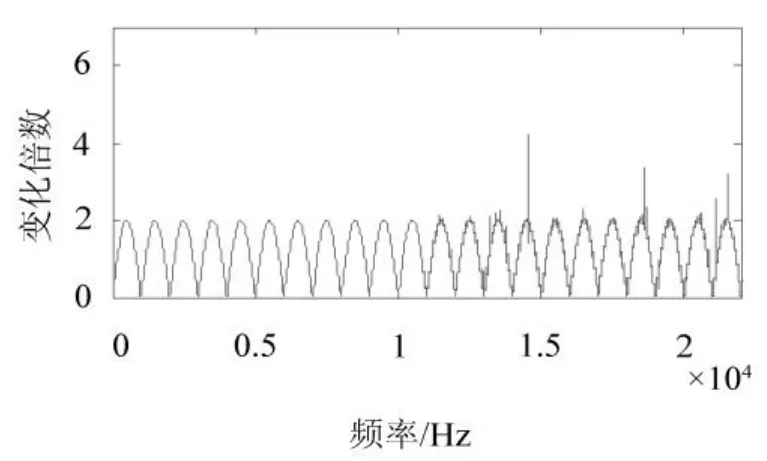
图4 延时0.001 s时叠加信号与原信号频谱的比值Fig.4 Specific value of superposed signal and primary signal when delay time is 0.001 s
当延时时间为0.002 s时,绘制叠加信号与原信号比值图如图5所示。与延时0.001 s时波形图比较可以看出,延时为0.002 s时,在低频部分同样遵循周期正弦分布的规律,最大幅值也为2,且周期为500 Hz,说明叠加信号变化倍数的周期是延时时间的倒数,即周期=1/延时时间。通过比较,其规律与式(3)相同,用式(3)可表示图4、5的波形,说明仿真实验控制结果与理论分析相同,适用于实际有源噪声控制过程。同理,式(4)所示相位变化规律也应符合实际,在此不再进行仿真说明。
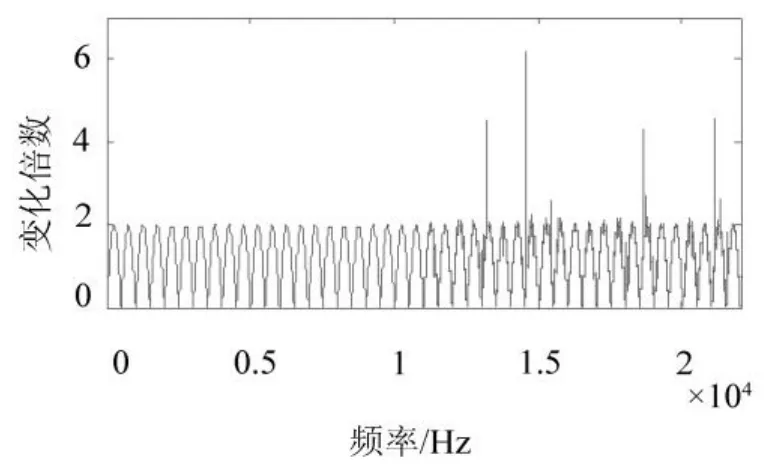
图5 延时0.002 s时叠加信号与原信号频谱的比值Fig.5 Specific value of superposed signal and primary signal when delay time is 0.002 s
4 尖峰噪声的抑制
通过对采集信号进行频谱分析发现叠加后信号的幅值与原始信号幅值变化规律与式(3)所示规律相同,验证了理论分析适用于实际。根据式(3)对叠加后信号进行控制时,可确定控制后信号的幅值。式(4)表示延时叠加后信号的相位情况,对叠加后信号进行控制时,可确定控制后信号的相位。两者共同确定叠加后波形与原波形之间的关系,得出叠加后的真实波形,为进一步优化有源噪声控制降噪效果提供了便利。
4.1 尖峰噪声的抑制方法
通过既定公式进行控制的方法较其它方法更加简便,不需要依赖对象精确的数学模型,也不需要依赖专家知识和操作人员的经验规则,只需确定可能的延时时间,通过一系列的运算就可以在抗噪声源端将噪声抑制。控制过程如图6所示,频谱分析是对初始传感器采集到的初始噪声进行的,得出初始噪声各频率下的幅值和相位;控制表达式是傅里叶变换直接得到的关于幅值和相位变化的两个表达式,即式(3)、(4);构建波形是根据延时叠加后信号各频率下幅值和相位,构建出延时叠加信号的真实波形,发出与之相反的声信号进行噪声的抑制。根据延时叠加信号的幅值和相位,可用以下公式来表示延时叠加信号
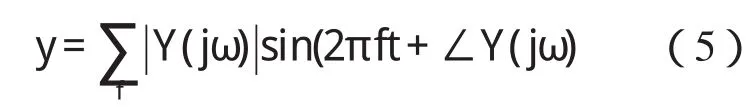
抑制尖峰噪声的步骤如下
(1)对原始声信号进行频谱分析,得出相应的幅值和相位;
(2)通过幅值相位变化表达式式(3)、(4),得出延时叠加后信号不同频谱的幅值和相位;
(3)通过式(5)构建延时叠加信号的真实波形,将其反向,并与ANC发出的有时滞的抗噪声信号进行叠加,形成最终的抗噪声信号;
(4)误差信号反馈给ANC进行下一周期的控制。
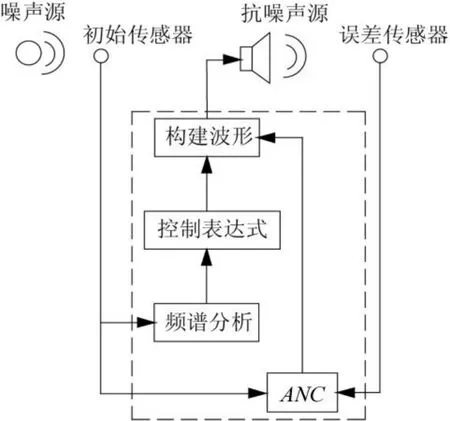
图6 抑制尖峰噪声示意图Fig.6 Schematic diagram of controlling peak noise
4.2 仿真验证噪声抑制的效果
仿真验证利用公式计算直接进行控制的降噪效果。取采集到的信号进行仿真,验证噪声抑制的效果。
根据叠加信号与原信号关系式,对采集信号进行处理,与直接通过函数FFT进行傅里叶变换得到的波形进行比较。通过Matlab编程仿真得到图7的结果,其中图7(a)是通过表达式(3)计算得出的,而图7(b)直接通过函数FFT进行傅里叶变换得到。将两图比较,发现两图相似,存在较小误差,说明通过式(3)可近似模拟延时叠加信号频谱特征,可得出延时叠加信号的真实波形。
图8(b)是直接通过仿真得出的延时叠加信号波形,图8(c)是通过前文得出的表达式,计算得出的延时叠加信号波形,比较发现两图相差无几,说明用公式计算是可以真实构建延时叠加信号波形的。图8(d)是抑制尖峰噪声处理后得到的信号,是利用公式计算直接进行控制的降噪效果图,从图中可看出信号幅值远小于原信号和延时叠加信号的幅值,降噪效果明显。
5 结语
本文针对抗噪声源时滞引起的尖峰噪声进行展开分析,理论分析出延时叠加信号幅值和相位的表达式,通过对随机噪声延时叠加后信号进行频谱分析,验证表达式适应于实际有源噪声控制系统。给出了一种通过公式计算直接进行控制的减小尖峰噪声的方法,仿真验证这种方法可以有效抑制尖峰噪声。
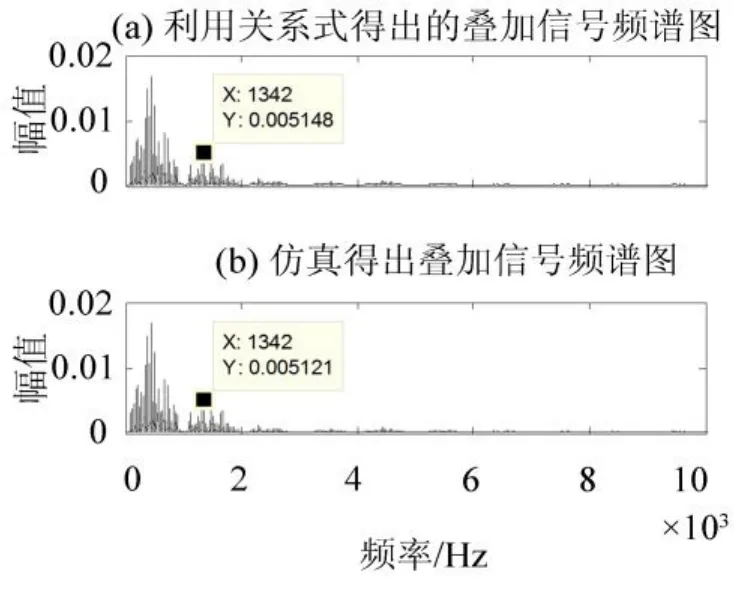
图7 分别利用关系式和仿真得出叠加信号频谱图Fig.7 Spectrums of superposed signal using expressions and using matlab directly
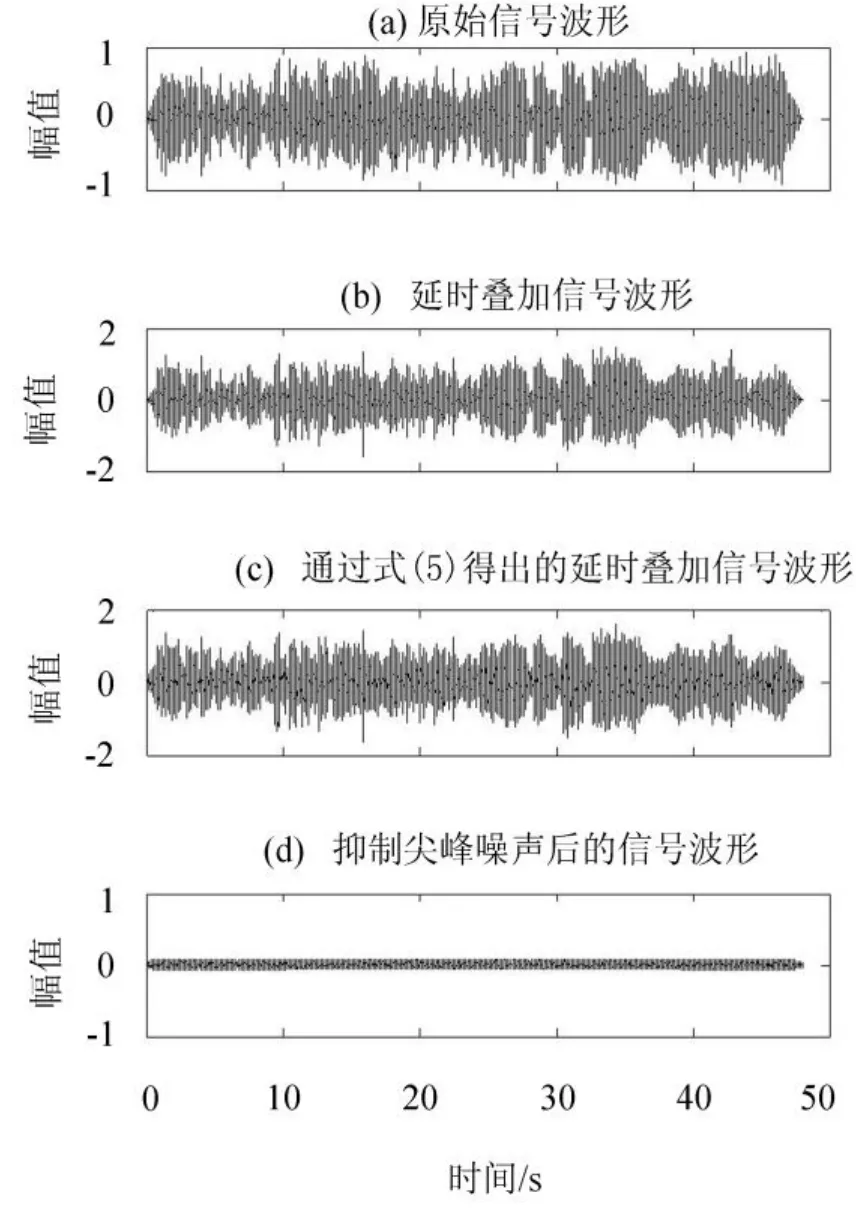
图8 抑制尖峰噪声仿真波形Fig.8 Waveform of controlling peak noise
[1]王进军,陈克安.有源噪声控制的现状及展望[C].第十八届全国振动与噪声高技术及应用会议,2005.4-6.
[2]刘日山.封闭空间噪声有源控制的研究[D].福建农林大学.2009.7-8.
[3]姚加飞,卢萍.抗噪声源时滞引起的尖峰噪声的抑制[J].噪声与振动控制,2012,14-17.
[4]Alan V.Oppenheim,Alan S.Willsky,S.Hamid Nawab.Signals&Systems[M].西安:西安交通大学出版社.2001.156-159
[5]陈克安,曾向阳,李海英.声学测量[M].北京科学出版社,2007.140-14.
