基于EMD和STFT柴油机缸盖振动信号时频分析

刘建敏，李晓磊，乔新勇，李华莹

（装甲兵工程学院机械工程系，北京 100072）

柴油机是一种结构复杂的往复机械，其表面振动是内部各种激振力共同作用的综合反映。一般来讲，缸盖振动的激振力可简单分为由燃烧引起的直接激振力和由机械工作时发生的间接激振力。直接激振力包括气缸内的气体压力、曲柄连杆机构的重力及惯性力；间接激振力通常有活塞侧向敲击、进排气门开启和落座以及喷油泵、喷油器等对缸盖的激振作用。

柴油机各激励源作用具有固定的时序且频率响应段有所不同，使振动信号呈现出很强的时频特性。各激励源的冲击特性，使柴油机缸盖振动信号类似于机械故障或损伤引发的声发射信号，即AE信号。该类信号由高频突发脉冲信号和长周期准平稳噪声信号组成，适宜用短时傅里叶变换描述其时频特征[1]。但一般的STFT算法由于窗函数的适应性不强，导致频率分辨率较低。文献[2]提出了一种窗长自适应的STFT算法，通过计算信号点的局部能量，优选窗宽，经验证该算法对于单分量信号，能够实现窗宽的自适应选择，提高了STFT的分辨率；但对于复杂的多分量信号，由于无法有针对性地选择窗函数类型，分辨率有所下降。文献[3]利用小波分解将潮汐形变信号分解为高频和低频两部分，并对高频部分进行STFT，得到了较为清晰的时频分布。但受小波基函数的限制，该方法分解过程的自适应性较弱，得到的小波包也并非单分量信号，对窗函数选择不能形成有效地指导。

利用振动信号评价柴油机燃烧状况及部件运行情况，首先要获得准确而清晰的时频分布。柴油机缸盖振动信号是典型的多分量信号，具有非平稳、非线性等特点。为了解决多分量信号窗函数及窗宽的选择问题，提高缸盖振动信号STFT的时频分辨率，本文尝试将经验模式分解（EMD）与STFT相结合，利用EMD筛选出缸盖振动的单分量信号，有针对性的选择窗函数进行STFT，并通过线性叠加得到原始信号的STFT时频分布。

1 EMD分解的基本原理及特点

1.1 基本原理

EMD分解的思想就是将信号分解成为若干个相对平稳的、互不相关的本征模态函数（IMF）。

一个本征模态函数应满足下面2个条件[4]

1）整个数据序列中，极值点的数量与过零点的数量应相等，或最多相差一个。

2）在任一时间点上，信号的局部极大值和局部极小值定义的局部均值应该为零。

EMD方法首先要找出信号x(t)的局部极通过插值方式求出上下包络线；计算上下包络线的均值，记作m1；通过式（1）计算

重复上述步骤，直到得到的h1k满足本征模态数的条件，即认为h1k为第1个本征模态函数。记：c1=h1k如此计算下去，最终获得信号的所有本征态函数cn和残余分量rn，原始信号即可表示为

1.2 EMD分解的特点

(1)自适应的滤波特性

经验模式分解的分解过程依赖于信号本身，是自适应的。它从特征时间尺度出发，首先把信号中特征时间尺度最小的模态分离出来，然后分离特征时间尺度较大的模态，最后分离特征时间尺度最大的模态，因此可以把EMD方法看成是一个自适应的高通滤波器。

(2)完备性和正交性

所谓信号分解方法的完备性，就是把分解后的各个分量相加能获得原信号的性质。式（2）表示了信号分解和重构之间的关系，该式表明EMD分解方法具有足够的完备性。而正交性是指分解得到的各个分量之间相互正交的性质[5]。

2 STFT的基本原理及缺陷

2.1 STFT的基本原理

短时傅里叶变换（STFT）是一种固定时间窗的时频分析方法，其基本思想是：用窗函数来截取信号，假定信号在窗内是平稳的，采用傅立叶变换来分析窗内信号，确定该时间存在的频率，然后沿着信号时间移动窗函数，得到信号频率随时间的变化关系，就得到时频分布，信号h(t)的STFT定义为

其中g(t)是窗函数。

STFT是典型的线性时频表示，满足叠加原理[6]。以两个分量的信号为例，当

z(t)=c1z1(t)+c2z2(t)时，可得到

2.2 STFT存在的问题

STFT（频谱图）概念直接，算法简单，己经成为研究非平稳信号十分有力的工具，在许多领域得到广泛应用，如：信号瞬时频率估计等，并且成为其它时频方法的基础。但STFT有两个主要困难是无法克服的：一是窗函数的选择问题。对于特定的信号，选择特定的窗函数可能会得到更好的效果。然而如果要分析包含两个分量以上的信号，在选取窗函数时就会感到困难，很难使一个窗同时满足几种不同的要求；二是对于窗函数长度的选择问题。窗函数的长度与频谱图的频率分辨率有直接的联系。要得到好的频域效果，就要求有较长的信号观测时间（窗宽长），那么对于变化很快的信号，将失去时间信息，不能正确反映频率与时间变化的关系；反之，若取得窗函数很短，虽然可以得到好的时域效果，但根据Heisenberg测不准原理，这必将在频率上付出代价，所得到信号的频带将展宽，频域的分辨率下降。因此需要根据信号的实际情况选择适当的窗函数和折中的窗宽以得到最佳的时频分布[7]。

3 基于EMD和STFT的时频分析方法

为了解决STFT窗函数及窗宽的选择问题，本文提出将EMD分解与STFT相结合，该方法的理论基础为EMD的分解的完备性和STFT的线性叠加原理。以EMD分解为三个分量为例，方法流程如图1所示。

3.1 窗函数的选择

对随机过程的测量，一般选用汉宁窗、海明窗或布拉克曼窗，因为它们可以在不太加宽主瓣的情况下，较大地压低旁瓣的高度，从而有效地抑制了功率(能量)的泄漏。对于周期信号或准周期信号分析时选用凯塞窗、布拉克曼窗。对于冲击过程和瞬态过程的分析一般选用矩形窗而不宜采用汉宁窗或海明窗，因为这些窗起始端很小的权会使瞬态信号加权后失去其基本特性[8]。

高斯窗函数用于STFT可以取得良好的特性。首先，高斯窗函数可以满足Heisenberg不等式且达到下界，能取得最好的时频带宽乘积。其次，高斯窗函数可以同时满足变换的正交性和完备性。正交性保证了变换不是冗余的，完备性保证了信号能够从变换的分量中完全恢复[9]。另外，高斯窗函数是指数窗的一种，其频率窗函数的主瓣比指数窗的主瓣窄，分辨率较指数窗有所提高；无负的旁瓣，也没有旁瓣波动，不会引起计算谱中假的极大值和极小值，是用来截取类似AE类信号的最佳选择。

IMF均为单分量信号，实际应用时，可以针对各分量的特点，选择相应的的窗函数类型，以提高窗函数的适应性。

图1 EMD和STFT结合流程图Fig.1 Flowsheet of EMD and STFT;

3.2 窗宽的选择

由于EMD分解的滤波特性，各IMF分量大体按照频率由高到低的顺序排列，这就给窗宽的选择提供了有力的参考。对于高频分量，可以适当选择较窄的窗宽；而对于低频分量可选择较大窗宽以提高频率分辨率。本文在实际操作中，将针对各IMF设定不同的窗宽区间(an,bn)，并以时频聚集性指数为目标函数，进行窗宽寻优，得到能使各IMF分量的达到最佳时频分布的窗宽Hbest。所谓时频聚集性是指时频分布具有很好的时频局域性，即在时频平面上高度聚集。常用的时频聚集性准则为[10，11]

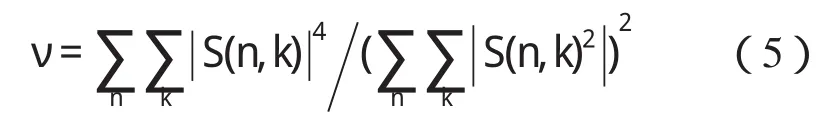
其中S(n,k)为时频图对应的时频矩阵。

4 柴油机缸盖振动信号分析实例

鉴于柴油机激励源众多，耦合严重，为了明确振动信号的物理意义，本文利用抽区间采样选择燃烧段的缸盖振动加速度信号为分析对象，如图2所示。

图2 燃烧段缸盖振动信号Fig.2 Cylinder vibration signal of combustion

文献[12]中指出L1段为针阀落座振动响应，其频率主要集中在6 kHz区域和32.5 kHz，L2则为燃烧爆发激励振动响应，其频率集中在8 kHz以下。对该信号直接进行STFT，得到时频分布如图3所示。该图基本上反映了信号频率随时间的分布，但分辨率较低，时频聚集性较差。经计算，其时频聚集性指标为2.448e-05。

4.1 缸盖振动的EMD分解

对振动信号进行EMD分解，得到11个IMF分量，如图4所示，分量按照频率由高到低的顺序排列；前5个分量保留了原始信号中的高频冲击成分，与AE信号较为类似，故选择高斯窗作为窗函数；中间3个分量为信号的低频部分，冲击性较弱，选择汉明窗较为合适。最后3个分量为信号的趋势项，不列入后期计算。

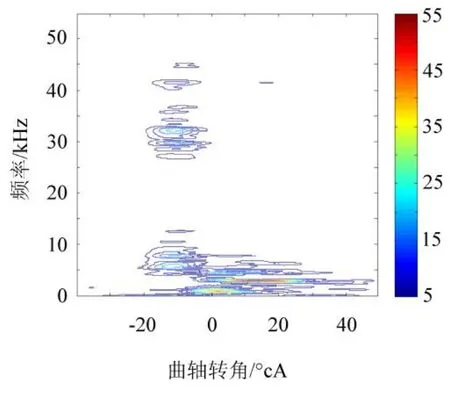
图3 燃烧段缸盖振动信号STFT时频图Fig3 STFT time-frequency figure of cylinder vibration signal friom combustion motivation

图4 振动信号的各IMF分量Fig 4 IMF of vibration signal

4.2 组合STFT的实现

在选定窗函数的基础上，对各分量进行STFT。预先设定窗宽搜索区间(an,bn)，通过窗宽寻优找到最佳的时频分布。当最佳窗宽为边缘值an或bn时，相应向an方向或bn方向移动窗口，继续寻优，直到Hbest值位于(an,bn)中。前五个分量频率成分较高，因此选择较小的窗宽值范围作为搜索区间，后3个低频分量则选择了较大的窗宽值搜索区间。详细设置如表1所示。为了保证计算精度，搜索步长均设置为2。

表1 窗宽寻优设置Tab.2 Installation of best window width searching

经过计算得到各分量的最佳窗宽及相应的时频聚集性指标，如表2所示。由数据可以看出，最佳窗宽值大部分分布在预先设定的搜索范围之内，这表明根据分量频段设置不同的搜索区间基本符合实际情况。其中IMF4和IMF8由于初始计算的最佳窗宽为边界值，故调整了搜索区间，最终得到的最佳窗宽偏大，可能是二者低频成分能量较大造成的。

表2 最佳窗宽及其时频聚集性指标Tab.2 Best window width and the Time-Frequency aggregation index

鉴于篇幅有限，每个搜索区间仅列出1个分量的最佳时频分布图。图5为第1个IMF分量的STFT，可以看出在33 kHz附近表现出良好时频聚集性。图6为第8个IMF分量的时频图，准确描述了信号的低频分布。

将各IMF的最佳STFT时频分布线性叠加，得到综合时频分布，如图7所示，其时频聚集性为2.5616e-05，较直接STFT有了明显提高，各激励的响应时刻及频率范围较图3更加清晰。

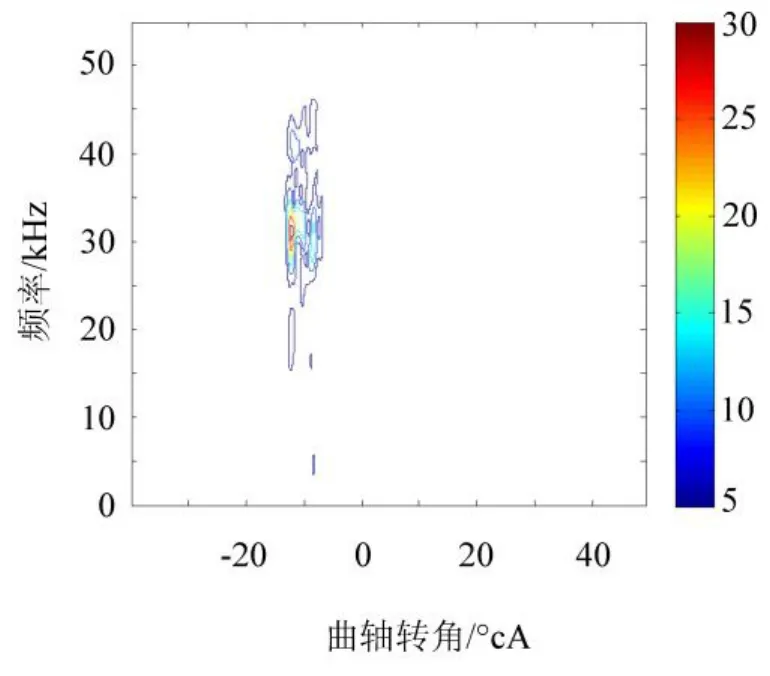
图5 IMF1最佳时频分布Fig.5 The best time-frequency distribution of IMF1

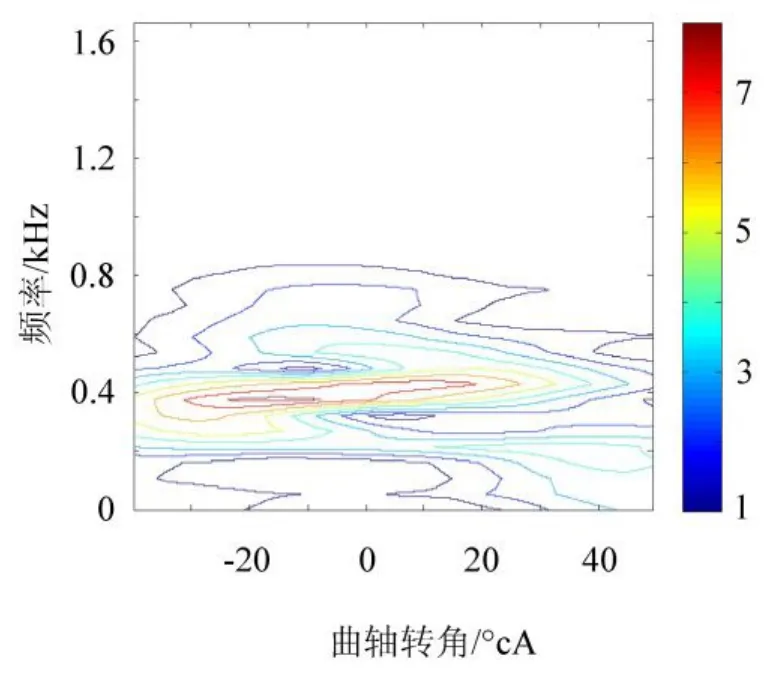
图6 IMF8的最佳时频分布Fig.6 The best time-frequency distribution of IMF8

图7 组合STFT时频图Fig.7 Combination STFT time-frequency figure

5 结语

提出了基于EMD和STFT的组合时频算法，分析了柴油机缸盖振动信号的时频分布特征。结果表明该方法具有以下的优点

(1)EMD可将复杂的多分量信号线性地分解为单分量信号，提高了STFT中窗函数选择的针对性；

(2)EMD的自适应滤波特性可以有效剔除信号的趋势项，确保了信号的准确度，同时消除了组合STFT的冗余计算量；不同的IMF分量分布在由高到低不同的频率段，可以指导窗宽的选择范围，提高了最佳窗宽搜寻效率；

(3)基于EMD的STFT算法可清晰描述柴油机缸盖振动信号的时频分布，真实反映激励源响应特性，为通过振动信号评价柴油机燃烧状况及部件运行情况奠定基础。

[1]廖传军，李学军，李德顺.STFT在AE信号特征提取中的应用[J].仪器仪表学报，2008，29（9），1862-1867.

[2]栾海妍，江桦，刘小宝.自适应短时傅里叶变换算法的研究[J].通信技术，2007，40（8），1-3.

[3]吕品姬，赵斌，陈志遥，等.小波分解-STFT方法在地形变观测数据中的应用[J].2011，31（5），136-140.

[4]杨晓红，杨晓静，朱霄珣.基于EMD的支持向量回归机振动数据挖掘[J].煤矿机械，2010，31（11），252-254.

[5]于德介，程军圣，杨 宇.机械故障诊断的Hilbert-Huang变换方法[M].北京：科学出版社，2006，32-33.

[6]张贤达，保铮.非平稳信号分析与处理[M].北京：国防工业出版社，1998，19-20.

[7]张宁，刘喜武.自适应时频分析及其时频属性提取方法研究[D].青岛：中国海洋大学硕士学位论文，2008.

[8]杨艳娟.窗函数的适用性分析[J].煤炭技术，2007，26（2），124-126.

[9]边海龙，陈光禹.基于STFT和神经网络相结合的时变谐波检测方法研究[J].测控技术，2007，26（12），11-14.

[10]Williams W,Brown M,Hero A.Uncertainty,information and time-frequency distribution[J].Proc.SPIE,1991,1566:144-156.

[11] Jones D,Parks T.A high resolution data-adaptive time-frequency representation[J].IEEE Trans.Acoust,Speech,Signal Processing,1990,38(12):2127-2135.

[12]史玉鹏，刘建敏，许世永，等.基于缸盖振动的柴油机喷油—燃烧信息检测研究[J].车用发动机，2011，6，74-82.