改进的小波阈值函数滤波分析
2013-02-24赵晓燕
赵晓燕
(1.上海市政工程检测中心有限公司,上海 201114;2.上海市政工程设计研究总院(集团)有限公司,上海 200092)
小波分析是一种信号的时间—尺度(时间—频率)分析方法,具有多分辨分析的特点,并且在时频域均能很好地表征信号的局部特征,是一种窗口面积固定不变,形状可变,时间窗和频率窗都可以改变的时频局部化分析方法,被誉为数学显微镜。小波分析成功的应用领域之一就是信号消噪,该领域正在受到越来越多的关注,开辟了采用非线性方法去噪的先河。
在小波降噪方面,最早出现的是由斯坦福大学的Donoho提出的VisuShrink阈值去噪方法。此后各种小波去噪方法不断产生,如奇异性检测法,阈值法,比例萎缩法以及相关法等。在这些降噪方法中,阈值方法计算简单而且实用[1],缩短了信号的降噪处理时间,适合应用于健康监测系统中的信号处理[4]。本文在分析了软硬阈值方法的利弊后,结合小波分析的基本理论以及压电陶瓷传感器监测信号受噪声干扰的特点,对Donoho提出的统一阈值进行了修正,并对仿真信号进行滤波,结果表明,该算法优于传统的阈值法,并能够将有效信号提出。
1 小波分析[1―3]
小波即小区域的波,“小”是指其在时域中具有紧支集或近似紧支集,“波”则是指该函数具有正负交替的波动性。小波分析以傅立叶变换为基础,并对傅氏变换函数进行改进,即以能够改变形式和窗口大小的小波函数来代替傅氏变换中唯一使用的函数e-jωt。小波函数是在能量有限的信号空间中满足其傅氏变换Ф(ω)有限可积条件的函数
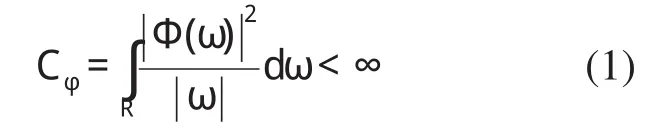
上式中,Ф(ω)是小波函数φ(t)的傅氏变换。根据付氏变换原理,Ф(ω)为连续函数,同时,为了能够满足小波变换重构条件,Ф(ω)在原点处必须等于0,即

进一步对小波函数进行伸缩和平移变换,即可得到一系列的小波函数列,
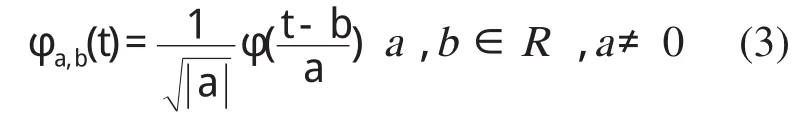
根据傅氏变换的原理,对任意函数进行连续小波变换可得
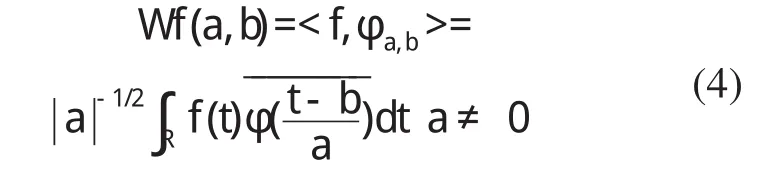
对小波变换系数Wf(a,b)进行逆变换,得到相应的原函数重构公式为

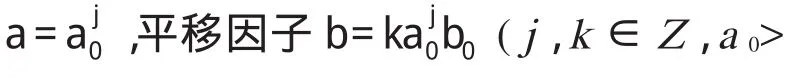
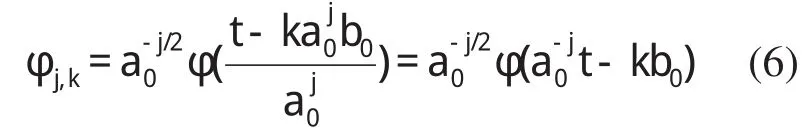
采用上述离散化小波函数对任意信号进行离散小波变换可得
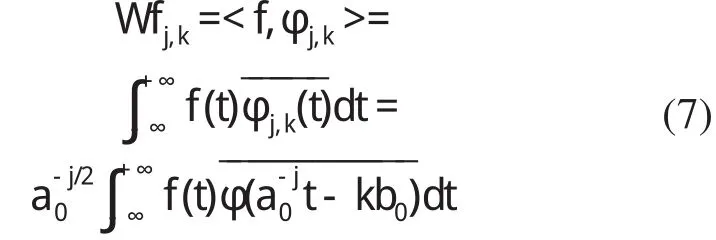
相应离散小波变换的重构公式为
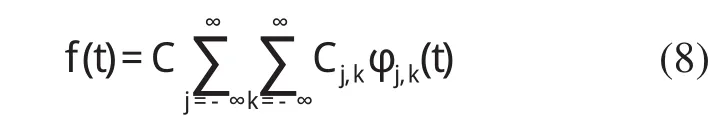
式中C为与原始信号无关的积分常数。
由式(3)可以看出,连续小波变换的时频窗口是可变的,其窗口形状为变化的矩形[b-aΔφ,b+aΔφ]×[(±ω0-ΔΦ)/a,(±ω0+ΔΦ)/a],并且窗口的中心位置位于点(b,±ω0/a)。根据小波函数变换的窗口尺寸计算其窗口面积S,可得

式(9)说明小波变换的时频窗口面积是与尺度因子和平移因子无关的量。尺度因子a越大,时频窗的时宽边越短,从而对信号中的高频成分具有较高的时间分辨率;a值越小,时频窗的时宽边越长,对信号中的低频成分具有较高的频率分辨率。
如果在对小波变换进行离散变换的过程中,使分解尺度按二进制变化,可以得到小波函数
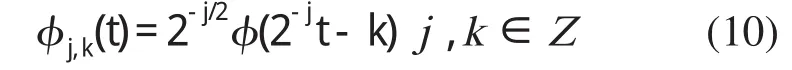
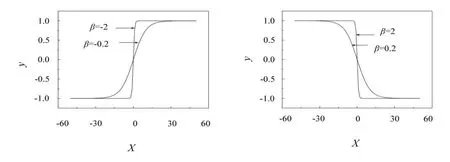
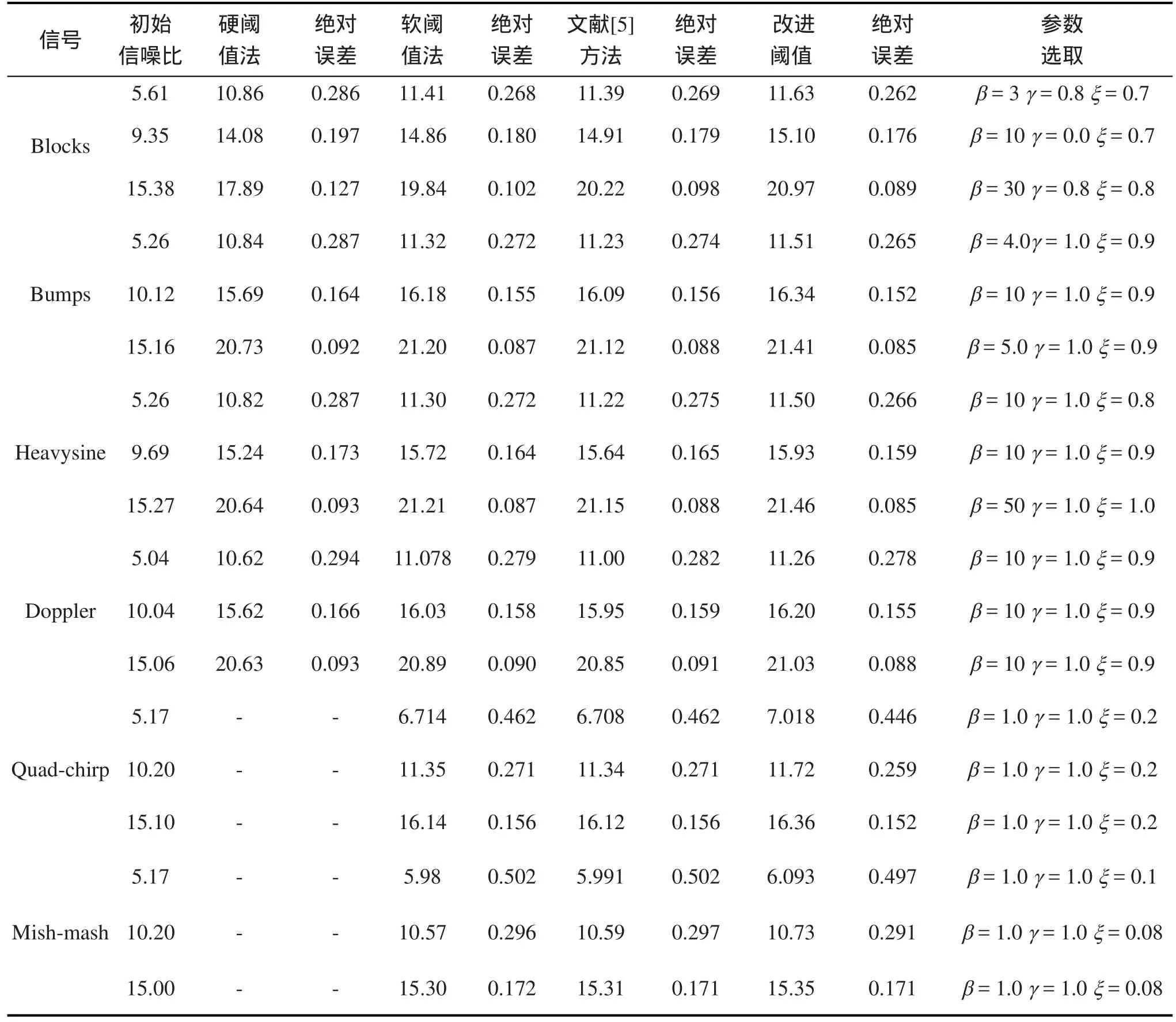
当存在常数A和B,满足0 那么式(10)中的函数即为二进小波。当常数A=B时,为二进小波变换的最稳定条件。由式(10)可以看出二进小波在保持时间域连续变化的前提下,仅对尺度参数进行了离散,保证了时间域变化的连续性。 利用二进小波,对分析信号进行变换可得二进小波函数序列 由二进小波变换可以看出,信号在经过每级尺度分解之后,分解信号的长度与原始信号的长度一致,存在着冗余信息,但是相对于离散正交小波变换来说,冗余数据在分解信号重构的过程中,能够更好地使小波系数得到处理,并且能够避免人工噪声的引入,提高原始信号的信噪比。 通常的一维高斯白噪声信号以线性叠加的方式作用于真实信号,具体可以表示为式(14)的形式 上式中f表示真实信号;e表示噪声;σ表示噪声水平(噪声强度)。由于信号经小波分解后在各尺度上满足线性叠加关系,则带噪信号经二进小波分解后的小波系数可以表示成真实信号的小波分解系数与噪声信号的小波分解系数的叠加,即由于在尺度j上,噪声e的小波变换系数模值为 并且噪声中任意两点乘积的数学期望为 所以噪声e的小波变换系数模值的数学期望为 由上式的推导结果可知,噪声小波系数模的期望值与其强度成正比,与小波分解尺度成反比。这就表明,在信号的小波分解中,随着分解尺度的减小,噪声信号的小波系数模值呈增大趋势,而此时信号的小波系数呈减小趋势,即在小波分解的小尺度上,高频噪声所占比例成分较大,因而据此可以对信号进行降噪处理。 根据噪声和信号在不同小波分解尺度上的不同传递性,以最大限度去除小尺度对应系数的干扰,重构得到较真实信号,即为阈值法,过程中选取的限度值就是阈值。如果令ωk,j和ωk,j分别表示处理前后的小波分解系数,T为阈值,则阈值法可以表示为 式(19)和(20)分别给出了软、硬阈值算法的表达式。可以看出,两种算法对小于阈值的小波系数均采用置零的方法;对大于阈值的系数,软硬阈值的处理方法各有不同。可以看出,硬阈值法虽然能去除大部分噪声,但是其将小于阈值的小波系数置零,会造成小波系数的不连续。软阈值法虽然保证了信号的连续性,但在信号重构时,会留下恒定的偏差。设想,如果将阈值前乘以系数α,以保证对小波系数进行降噪处理后的连续性,如式(21) 可以得出,在上式中,当α为0和1时,分别对应硬、软阈值法的情况。可见,软硬阈值法是阈值法信号降噪处理的两个边界。因此,恰当的α函数是提高阈值法降噪效果的关键之一。 目前,阈值系数α具有多种形式,各具优点,考虑到小波系数去噪后的连续性以及在健康监测中应用的可行性,本文在文献[5]中所提出的阈值函数的基础上提出一种新的α函数形式。 图1 Sigmoid函数Fig.1 Sigmoid function Sigmoid函数(式(22))是误差反向传播神经网络经常使用的一种传递函数,其能够将整个实数范围内所有的神经元输入映射到区间(0,1)之间,而且该函数无穷可微,具有稳定的上下边界。由Sigmoid函数图可以看出该函数能够随着自变量的增大而无穷逼近固定的边界,这种变形非常满足阈值系数α的选取条件。可以验证,在类Sigmoid函数(23)中,自变量系数β的大小关系到函数曲线的缓和程度,β的正负关系到曲线的增减性,如图1。根据阈值函数在小波去噪中的特点,将图1中的类Sigmoid函数沿零点进行旋转、变形,得到新的阈值函数,式(24)[6],函数图形如图2中的各图所示。由图2可以看出,在改进的阈值函数的α系数中,参数β控制了阈值函数的平缓程度,参数ξ控制了阈值函数的去噪起始点,参数γ控制了函数在软硬阈值间的逼近程度。可以看出,随着各参数的改变,降噪处理之后的小波系数在硬阈值和软阈值边界范围内变化。改进后的阈值函数仍然具有Sigmoid函数的无穷可微性,从而保证了去噪之后小波系数的连续性。而且参数γ和ξ的引入,使得去噪后的小波系数更贴近于原始信号,减小了软阈值函数去噪后留下的恒定偏差。 图2 改进后的阈值函数在不同系数取值下的曲线Fig.2 Improved threshold function with different coefficient value 阈值降噪法中,在阈值函数确定以后,另一个关键点就是如何估计阈值。目前估计阈值的方法主要有统一法,自适应估计法以及极大极小原理选择法等[1]。 从带噪信号的表达式中可以看出,噪声强度是构成原始信号的变量之一,而在实际工程中带噪信号的噪声强度是未知的,因而选取阈值时首先要对噪声水平进行估计。 通常在最简单的带噪信号模型中,认为e是均值为零的高斯白噪声,其噪声水平等于1。但是在大多数情况下,采集信号的噪声是未知的,此时噪声的方差可以使用小波分解系数的中位数来估计[7],即 但是,当带噪信号在小波变换的支集上有突变的情况下,小波变换系数会很大,那么此时小波分解系数中信号的能量占主导地位,此时以式(25)来估计噪声的强度会引入很大误差[8]。对于此种误差,可以事先不考虑突变下的小波系数[8],而采用该尺度上的其他小波系数进行噪声强度估计。本文采用该方法,首先对每层小波分解系数进行噪声强度估计,然后计算最优预测变量阈值,对信号进行降噪处理。 为了验证改进阈值函数的有效性,选用6种典型噪声信号进行降噪仿真验算。Symlets小波系是由Daubechies在db小波函数上进行改进而提出的近似对称的小波函数,其在支持长度、对称性以及正交性等方面均具有更好的性能。经分析,‘sym8’小波具有较光滑的波形和较好的频率特性,本文中选用此种小波对带噪信号进行分析。过程中将信号使用‘sym8’小波进行6层分解,并对前5层小波分解系数进行滤波处理。 以Blocks, Bumps, Heavy-sine, Doppler,Quadchirp,Mishmash信号为例,分别选取不同信噪比的噪声信号进行消噪验算。由于每种噪声信号的特性各不相同,过程中调整参数β,γ和ξ,以使滤波结果达到最优。为便于比较,在不同信噪比信号滤波过程中,均取同类的阈值。将降噪处理之后信号的信噪比和均方误差与基于离散小波变换的软硬阈值法以及文献[5]中滤波方法所得结果进行比较,列入表1。这里,误差评价的计算公式为: 表1 改进阈值法与软、硬阈值法去噪效果比较Tab.1 Comparison of the effectiveness of soft,hard and improved threshold function 式中s为降噪处理后的信号;s0为原始带噪声信号。信噪比的计算公式为: 其中,ps为降噪后信号的能量;pn为降噪前信号的能量。 图3 Bumps信号降噪Fig.3 Filtered signal of bumps 对后两种噪声信号的硬阈值法滤波来说,中空出的数据表示对应此种降噪情况下,所得信号严重失真,因而这里不给出其降噪后的信噪比。 为更好地说明采用本文改进的阈值函数进行信号降噪的有效性,本文给出采用不同阈值方法降噪后的波形。但限于篇幅,这里以包含频率成分丰富的Bumps信号为例,设定其信噪比为5,将采用软、硬阈值以及文献[5]算法和改进阈值法处理后的信号进行比较,如图3。 从表1中的数据可以看出,改进的阈值法较传统的软硬阈值法对不同信噪比的信号在信噪比和降噪误差上均有不同程度的提高;比较图3至图4中的各图,当信号的信噪比较低时,基于离散小波变换的硬阈值算法产生的重构噪声较大,软阈值算法虽然较由硬阈值算法所得信号光滑,但是其与原始信号具有恒定的偏差,文献[5]算法虽然保证了信号的连续性,但是在滤波后的信号中仍然有较多的微小噪声存在,而这些不足在由本文改进的算法中均能够较好地避免。即采用本文基于二进小波的改进阈值法降噪后的信号能更加逼近于原始信号。 本文基于二进小波分析,采用变形的Sigmoid传递函数对传统小波阈值函数进行了改进,并采用该方法对6种带噪声信号进行滤波仿真。计算结果表明,改进的阈值算法能够有效地提高原始信号的信噪比。 [1]胡昌华,李国华,等.基于MATLAB 6.x的系统分析与设计—小波分析(第二版)[M].西安:西安电子科技大学出版社,2004. [2]成礼智,王红霞,罗永.波的理论与应用[M].北京:科学出版社,2004. [3](美)Ingrid Daubechies著.李建平,杨万年译.小波十讲[M].北京:国防工业出版社,2004. [4]赵晓燕,李宏男.一种基于改进的小波分析消噪方法及其在健康监测中的应用[J].振动与冲击,2007,26(10):137-139. [5]曲天书,戴逸松,王树勋.基于SURE无偏估计的自适应小波阈值去噪[J].电子学报,2002,30(2):266-268. [6]赵晓燕.基于压电陶瓷的结构健康监测及损伤诊断[D].大连:大连理工大学,2008. [7] David L Donoho.De-noising by soft-thresholding[J].IEEE,Transactions on information theory,1995,41(3):613-627. [8]刘毅华,赵光宙.故障分析中的小波软阈值改进除噪方法[J].继电器,2004,24(32):15-19.
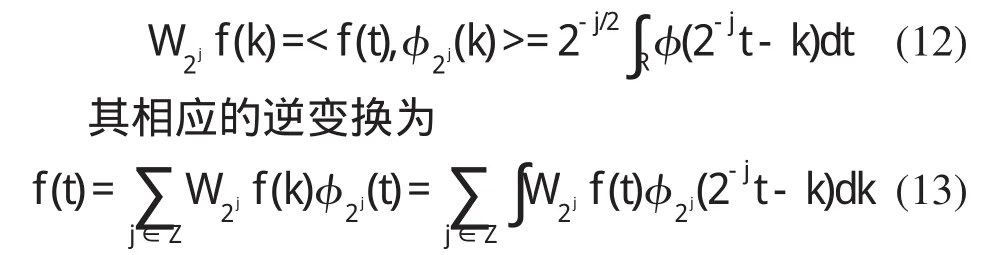
2 阈值法及其改进
2.1 噪声表达




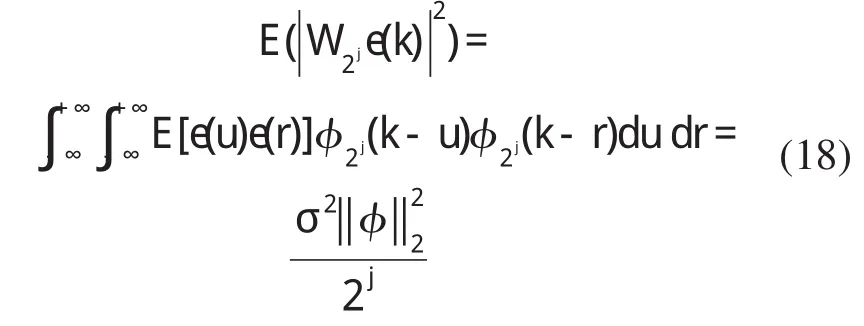
2.2 阈值函数及改进




2.3 阈值估计

3 仿真分析



4 结语
