闭口薄壁截面圆弧拱空间动力稳定性分析

董宁娟，赵洪金

（1.中国飞机强度研究所，西安 710065；2.西安建筑科技大学土木工程学院，西安 710055）

薄壁曲梁因其流线造型在桥梁工程和建筑工程中得到了广泛的应用。曲梁不同于直梁之处在于初始曲率的存在，这使得其弯曲、扭转、翘曲的几何方程大多是相互耦合的，其变形常为弯扭变形，导致了曲梁理论分析的复杂性。对于任意的薄壁曲梁,在承受周期性动载荷情况下，有可能发生剧烈的横向振动、扭转振动或弯扭耦合振动，从而导致薄壁曲梁的动力屈曲，即所谓的参数共振[1]。研究一般薄壁压件和薄壁直梁的动力稳定问题文献已有报道[2―10]。对于薄壁曲梁的动力稳定性问题的研究还鲜有报道。

本文针对薄壁构件较一般杆件更容易发生动力屈曲，且动力屈曲的形式也更为复杂的问题，专题研究薄壁截面圆弧拱在周期性动载荷作用下的动力屈曲。通过能量法和Hamilton原理推导出薄壁圆弧拱动力稳定性方程，利用Galerkin方法将其转化为二阶常微分Mathieu-hill型参数振动方程，求得周期解所包围的动力不稳定区域，为工程结构动力设计提供参考。

1 空间动力稳定微分方程

受均布径向荷载作用下的圆弧拱，其拱轴在侧倾后是其位移和变形的几何关系用曲线坐标x轴(侧向)，y轴(径向)以及z轴(切向)来描述。图1为拱侧倾后拱轴上任意一点在x、y、z三个方向的线位移和角位移分别为面外侧向位移u、径向位移v、切向位移w、面内弯曲角β、面内弯曲角ψ以及侧向扭转角θ。

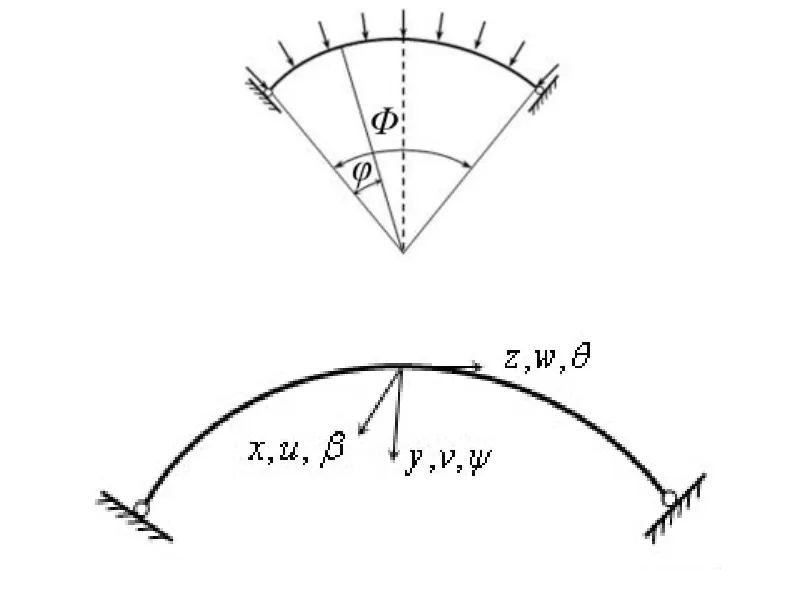
图1 圆弧拱空间几何参数Fig.1 Space geometric parameters of circular arch

发生空间失稳后，圆弧拱的应变能U等于侧向弯曲应变能和扭转应变能之和[11]，有

两端铰接圆弧拱在径向均布周期荷载q(t)=q0+qtc o sθt作用下，其压力线与拱轴线重合，拱内只产生轴力N=q R，为均匀受压的受力状态。外力势能V等于拱侧倾后外荷载所做功的负值，即

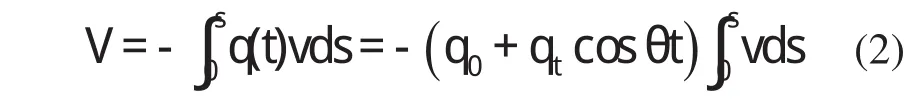
根据圆弧拱侧倾时拱轴不可伸缩条件

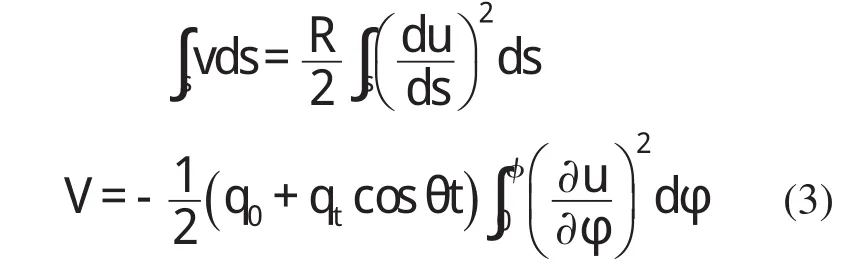
薄壁圆弧拱在周期径向荷载作用下空间稳定总势能为

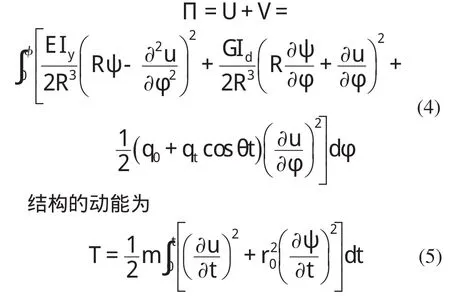
式中，其中r20=(Ix+Iy)A；u为平面外侧向位移，ψ为侧向扭转角，v为径向位移；Iy为圆弧拱的横截面对于y轴的惯性矩，EIy表示拱的横向抗弯刚度，G Id为扭转刚度，m沿拱轴的分布质量。

根据Hamilton原理，有

2 Mathieu-Hill型参数振动方程

对于两铰拱取位移函数为

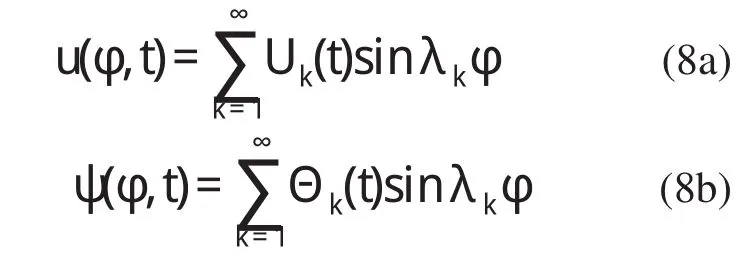
其中λk=kπϕ，ϕ为拱的圆心角。

满足拱的边界条件，利用Galerkin方法将式(8)代入方程(7)进行离散，可得到以下常微分方程组

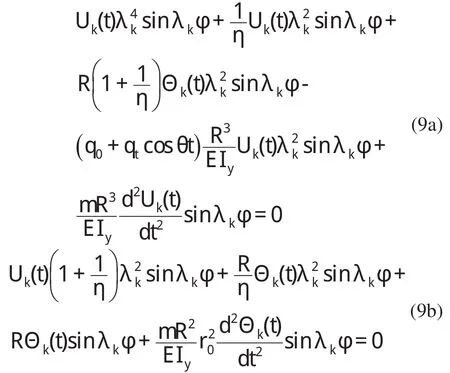
为了简化表达公式(9)写成矩阵的形式

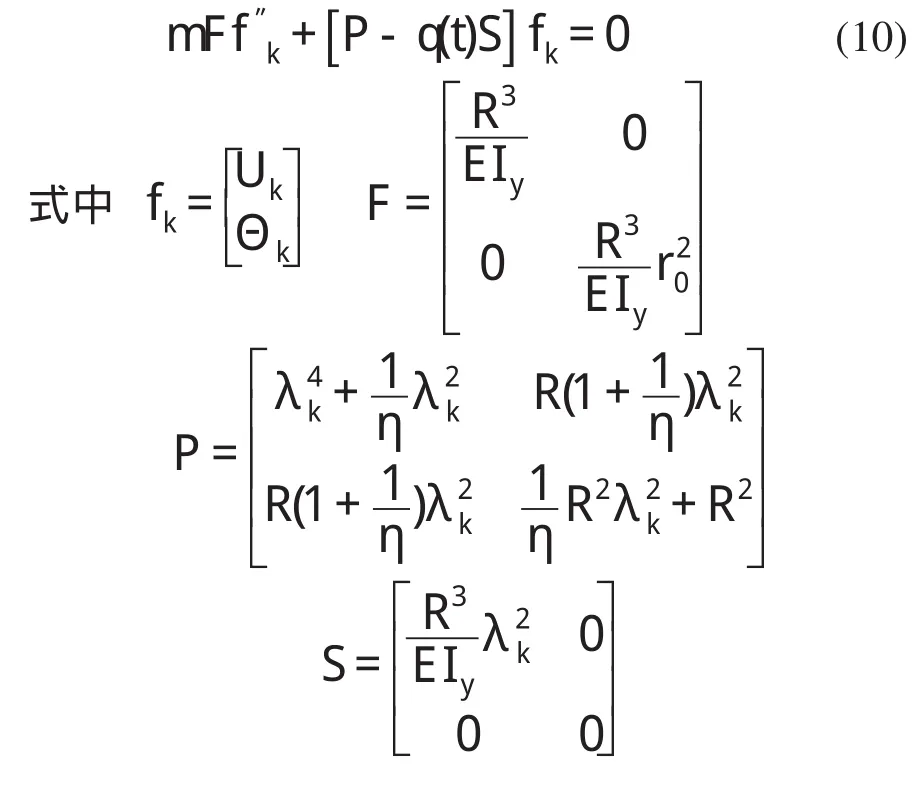
3 动力不稳定区域的确定

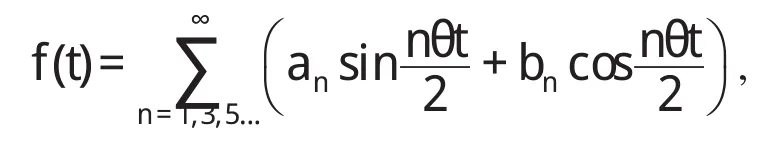
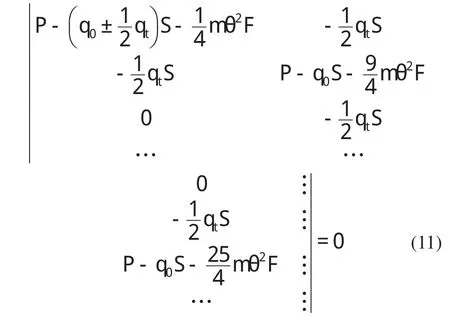
在求主动力不稳定区域时，可取方程式(11)第1阶主子式，即

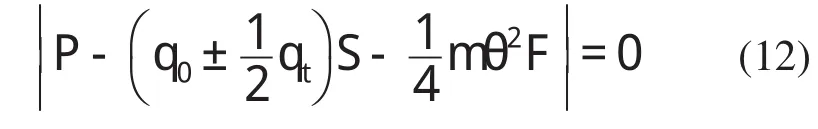
便有足够的精确度。由此即可解出位于θ=2Ω附近的动力不稳定区域边界。

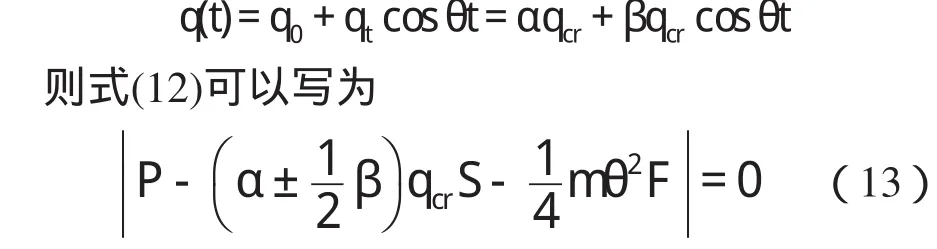
(1)α=1,β=θ=0时，|P-qcrS|=0对应于静力稳定问题；

(2)α=0,β=0,θ=2ω时，|P-mω2F|=0对应于结构自由振动问题；

(3)α∈(0,1),β=0,θ=2ω时，

|P-αqcrS-m Ω2F|=0对应于恒载下结构的自由振动问题。

因此参数共振问题就是静力稳定和自由振动的耦合问题。

对于有周期2πθ的周期解为

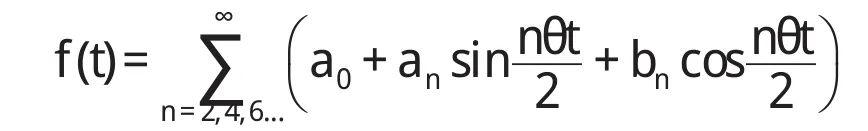
决定的动力不稳定区域,也可得到相似的方程。

4 算例分析

对于矩形薄壁截面圆弧拱，截面特性如下：A=0.3m2，Iy=0.00225m4，回转半径r0=0.3m，Iz=0.025m4，Id=0.007518m4，弹性模 量E=200GPa，剪切模量G=77.2GPa，单位长度上的质量为m=750kg/m。通过求解,确定动力不稳定区域分别如图2―图4所示。

由图2可知，随着动力荷载中恒荷分量的增加，结构发生空间参数共振时的频率也降低，动力不稳定区域扩大，但恒载对动力不稳定区域的影响相对较小。

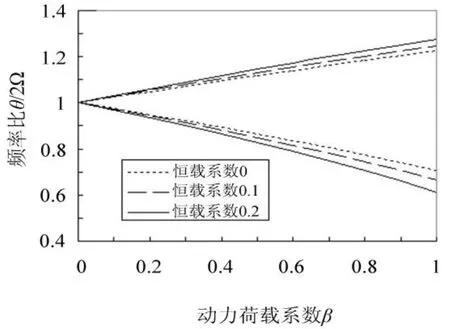
图2 恒载对圆弧拱空间动力不稳定区域的影响Fig.2 Effect of constant load on principal regions of dynamic instability for circular arch

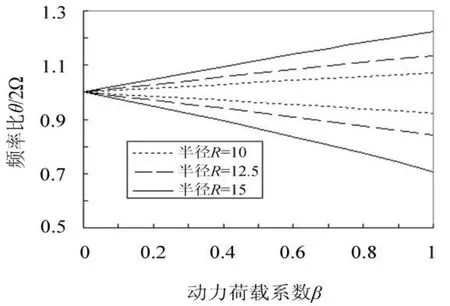
图3 半径对圆弧拱空间动力不稳定区域的影响Fig.3 Effect of radius on principal regions of dynamic instability for circular arch

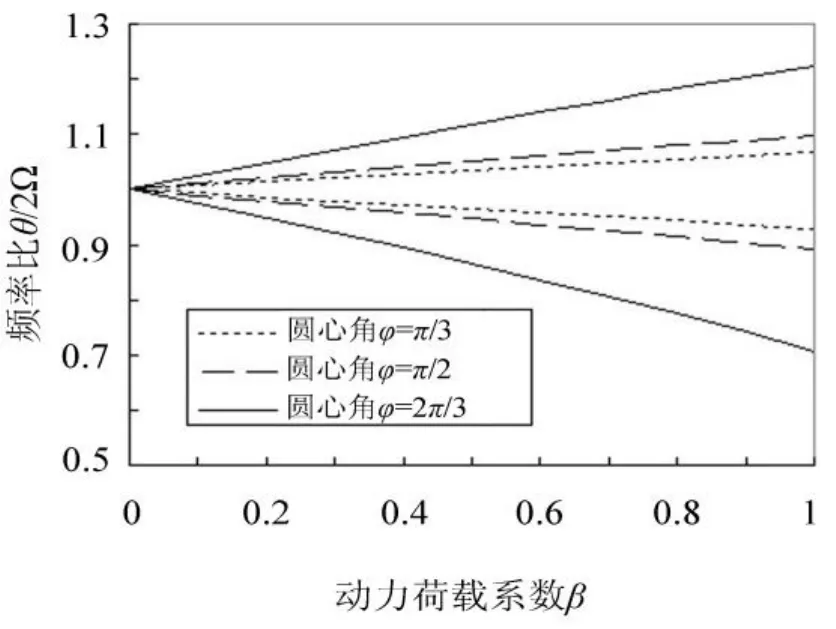
图4 圆心角对圆弧拱空间动力不稳定区域的影响Fig.4 Effect of central angle on principal regions of dynamic instability for circular arch

由图3可知，当圆心角为固定值时，随着圆弧拱半径增加，结构发生空间参数共振时的频率降低，动力不稳定区域迅速扩大，说明半径越大，发生参数共振的可能性也越大，因此圆弧半径是决定拱结构空间动力不稳定区域的重要因素。

由图4可知，当半径一定时，随着圆心角的增加，相应的结构发生参数共振时的频率也降低，动力不稳定区域扩大，说明圆心角越大，发生参数共振的可能性也越大，可见圆心角也是决定拱结构空间动力不稳定区域的重要因素。

5 结语

应用能量法和Hamilton原理，建立了径向均布周期荷载作用下闭口薄壁截面圆弧拱动力稳定平衡方程，求得周期解所包围的动力不稳定区域，探讨了恒载系数、圆弧半径以及圆心角等参数对动力不稳定区域的影响。恒载的增加会使圆弧拱空间动力不稳定区域变宽，与其它因素相比，其变化较小。随着圆弧半径和圆心角的增加，结构发生参数共振时的频率降低，动力不稳定区域迅速扩大，因此圆弧半径和圆心角是决定拱结构动力不稳定区域的重要因素。

[1]Bolotin,V.V.The dynamic stability of elastic systems[M].Holden-Day,INC.1961.

[2]童乐为，周国梁.偏心周期荷载作用下闭口薄壁构件的动力稳定性[J].上海力学，1992，13(2)：41-48.

[3]杨平，孙兰.偏心周期荷载作用下薄壁构件的动力稳定性[J].武汉交通科技大学学报，1998，22(4)：403-407.

[4]傅衣铭，宋丽霞.开口薄壁构件的非线性动力稳定性[J].湖南大学学报，1998，25(4)：9-14.

[5]S.P.Machado,V.H.Cortı´nez.Dynamic stability of thin-walled composite beams under periodic transverse excitation[J].Journal of Sound and Vibration,2009,32(1):220-241.

[6]C.Y.Lin,L.W.Chen.Dynamic stability of rotating composite beams with a viscoelastic core[J].Composite Structures,2002,58(2):185-194.

[7]P.Hagedorn,L.P.Koval.On the parametric stability of a Timoshenko beam subjected to a periodic axial load[J].IngenieurArchiv,1971,40(3):211-220.

[8]茅人杰，李军，凌复华.复合材料薄壁杆的动力稳定性[J].上海交通大学学报，1990，24(5、6)：186-196.

[9]茅人杰，孙国钧，雷中旺.轴压下各向异性开口薄壁杆的非线性共振[J].应用力学学报，1992，9(3)：8-18.

[10]罗漪.薄壁杆件的动力稳定性[D].华侨大学，2000.

[11]项海帆，刘光栋.拱结构的稳定与振动[M].北京：人民交通出版社，1991.