125I-103Pd复合近距离治疗源剂量参数的蒙特卡罗确定

曹 振 赵华立 谢 芹 张文在 冯跟胜 王晓静 张子健

1（原子高科股份有限公司 北京 102413）

2（中国核电工程公司河北分公司 石家庄 050019）

3（兰州大学 核科学与技术学院 兰州 730000）

4（中南大学湘雅医院肿瘤科 长沙 410008）

125I-103Pd复合近距离治疗源剂量参数的蒙特卡罗确定

曹 振1赵华立2谢 芹3张文在1冯跟胜1王晓静1张子健4

1（原子高科股份有限公司 北京 102413）

2（中国核电工程公司河北分公司 石家庄 050019）

3（兰州大学 核科学与技术学院 兰州 730000）

4（中南大学湘雅医院肿瘤科 长沙 410008）

根据AAPM TG43U1推荐的种子源剂量参数计算公式，得到125I-103Pd复合种子源剂量参数计算公式，并且推广到n种放射性核素复合种子源剂量参数计算公式。使用蒙特卡罗方法计算125I-103Pd复合种子源的剂量率常数、径向剂量函数和各向异性函数的数值，对径向剂量函数和各向异性函数进行拟合，得到经验公式。使用单一源125I的参数计算结果和相关数据进行了比较。得到单一源125I的剂量率常数为0.959(cGy·h–1·U–1)，与AAPM TG43U1中一种相类似的种子源6711(AH)的推荐值相差0.6093%。

蒙特卡罗方法，剂量学参数，125I-103Pd，经验公式

近几年，一种新型的125I-103Pd复合种子源开始应用于市场[1]。由于103Pd的半衰期为17 d，可以对快速增长的肿瘤细胞进行第一次精确的打击。而125I的半衰期为60 d，刚好可以继续清除残留的肿瘤细胞和杀死增长缓慢的肿瘤细胞[2]。一种新型的种子源要更好地应用于临床，则必须确定相关源的剂量计算参数。本工作将选择6711型125I的基本结构，将源改为125I-103Pd复合源，均匀涂在银棒上。使用蒙特卡罗计算复合源的各参数，同时推广到n种放射性核素复合种子源参数的蒙特卡罗计算。

1 种子源剂量计算相关公式

美国医用物理学家协会(American Association of Physicists in Medicine, AAPM)在2004年发布TG43U1报告，推荐种子源剂量计算公式如下[3]：

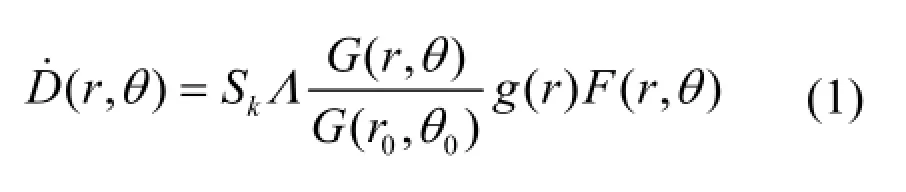
其中，Λ、g(r)、F(r,θ)即为所要求的种子源参数，r0、θ0为极坐标参考点的坐标，r0=1 cm，θ0=π/2。G(r,θ)为几何函数，具体计算过程可参考文献[3]。

放射性物质的活度不受外界环境的影响，对复合源参数的计算使用单一源的方式进行分步处理。

TG43U1推荐Λ计算公式如下[3]：

Λ是剂量率常数(cGy·h–1·U–1)。Sk是空气比释动能强度(cGy·h–1·cm2)，用符号U表示。

125I-103Pd复合源计算公式如下：

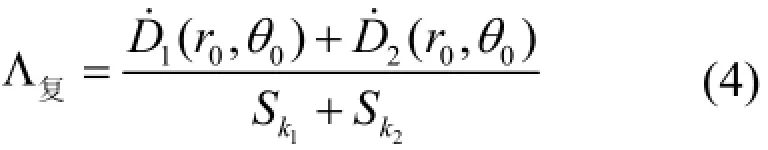
其中，1kS、2kS分别为125I和103Pd产生的空气比释动能强度为125I和103Pd在参考点处产生的吸收剂量率。下面125I-103Pd复合源计算公式中吸收剂量率的下标为1的均为125I在某点处产生的吸收剂量率，下标为2的均为103Pd在相同某点处产生的吸收剂量率。

推广到n种复合源的情况：

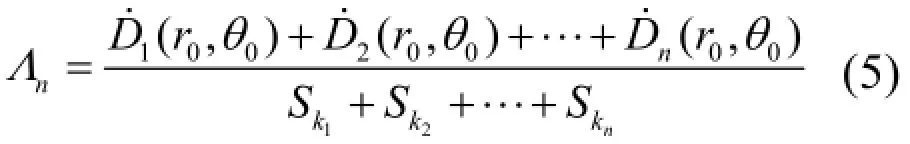
TG43U1推荐g(r)计算公式如下[3]：

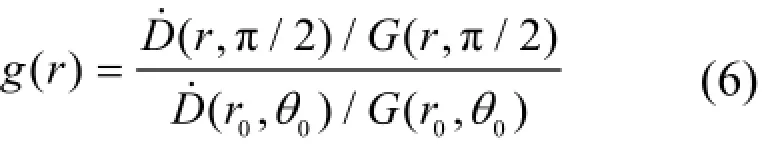
其中g(r)为径向剂量函数，G(r,θ)为几何函数。

125I-103Pd复合源计算公式如下：

推广到n种复合源的情况：

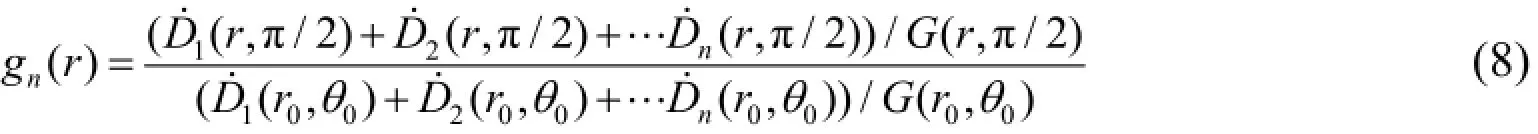
TG43U1推荐F(r,θ)的计算公式如下[3]：

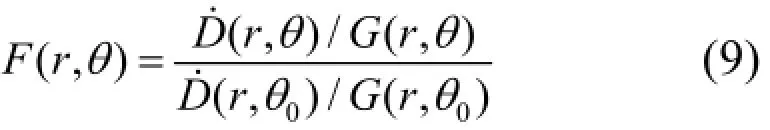
其中，F(r,θ)为各向异性函数，G(r,θ)为几何函数。

125I-103Pd复合源计算公式如下：

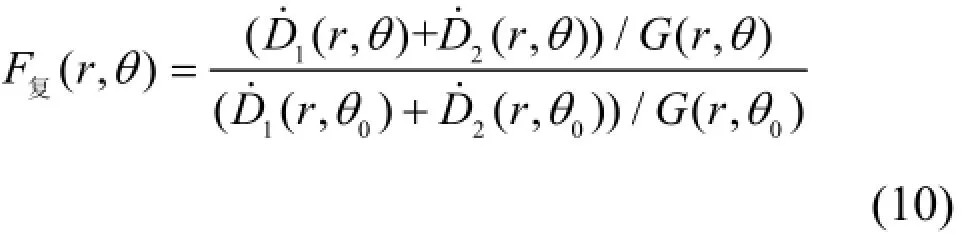
推广到n种复合源的情况：

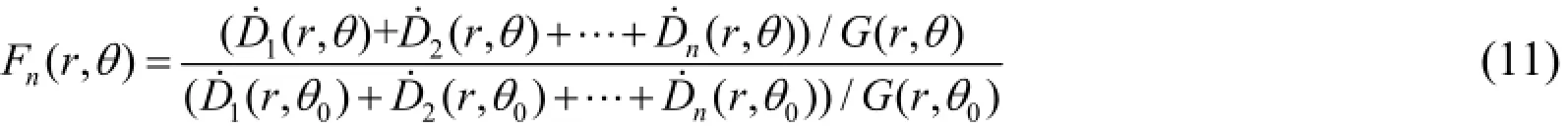
125I-103Pd复合源半衰期的计算公式：

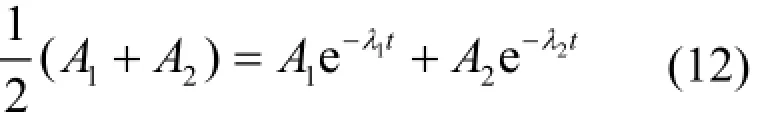
其中，A1、A2分别为125I和103Pd的初始活度，λ1、λ2分别为125I 和103Pd的衰变常数

此公式推广到计算n种复合源的半衰期公式：

2 蒙特卡罗模拟

2.1蒙特卡罗模拟使用的几何参数和相关的物理参数

研究中使用的种子源除了银棒表面电镀的放射性物质与6711型125I不同外，其余形状和物质的成分与6711型125I一样。本工作中银棒表面电镀活度为1:1的125I和103Pd放射性物质。其中两端的焊接点用半球近似，种子源长轴方向剖面图如图1所示。相类似的种子源结构可参阅文献[3–6]。

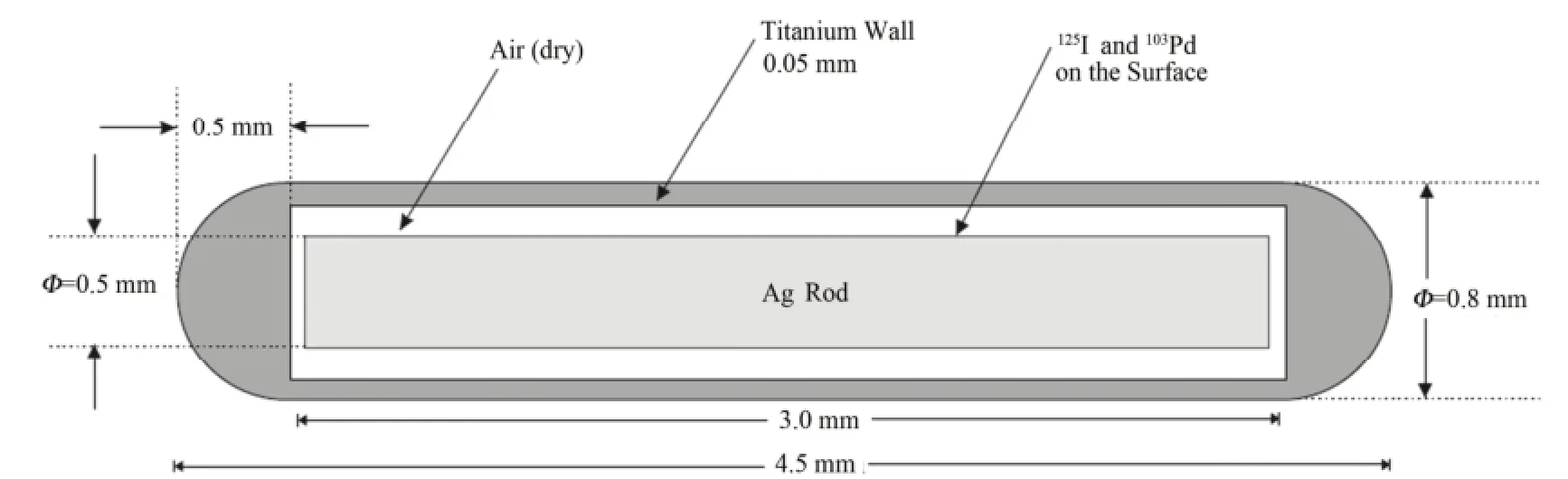
图1 新型125I-103Pd复合种子源长轴剖面图Fig.1 Longitudinal view of a novel seed source.

蒙特卡罗模拟过程中使用的核素[3]为125I和103Pd。125I的半衰期为(59.40±0.01) d，发射能量(括号内为每次衰变发射的光子数)，分别为27.202 (0.406)、27.472 (0.757)、30.98 (0.202)、31.71 (0.0439)和35.492 keV(0.0668)。103Pd的半衰期为(16.991± 0.019) d，发射能量分别为20.074 (0.224)、20.216 (0.423)、22.72 (0.104)、23.18 (0.0194)、39.75 (0.00068)、294.98 (0.00003)、357.5 (0.00022)和497.1 keV(0.00004)。种子源的材料列于表1。

本工作使用的蒙特卡罗软件为MCNP5[7]，光子截面数据来自ENDF/B-VI Release 8中的mcplib04，此数据库相比MCNP4C DLC-200数据库在低能光子的剂量计算上有改进，使低能光子的剂量计算更准确。

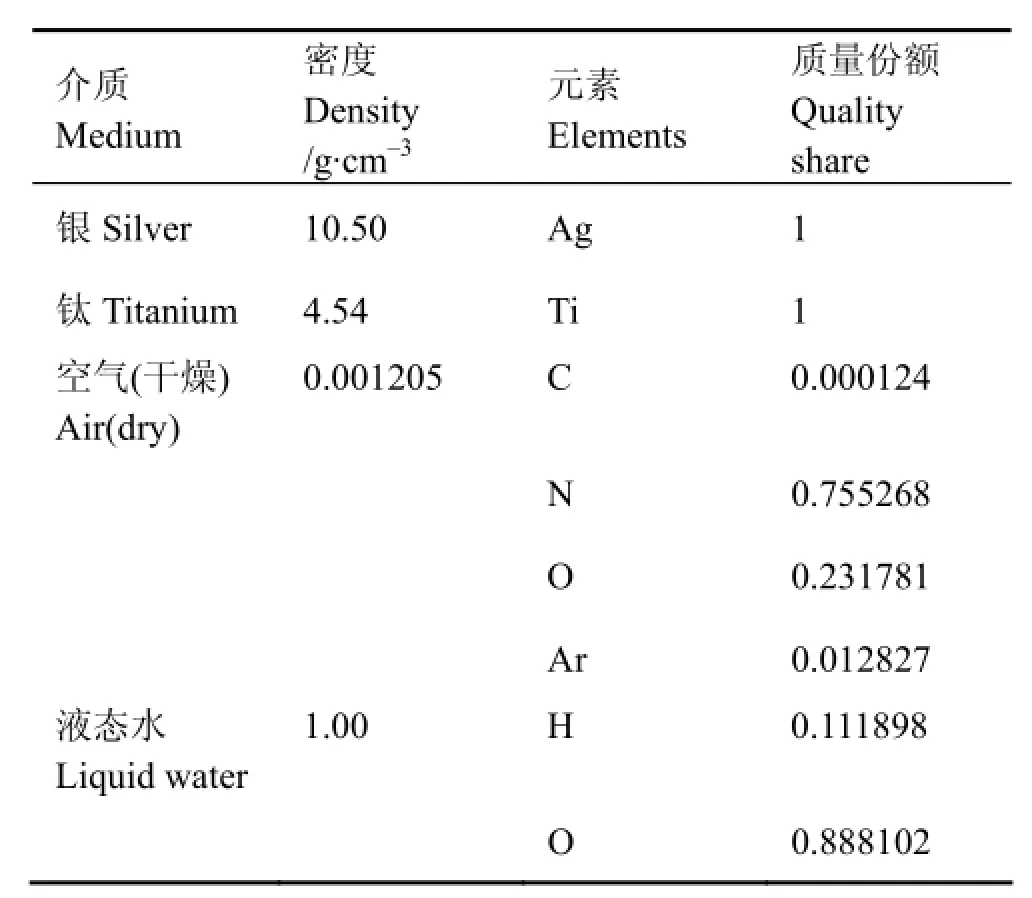
表1 蒙特卡罗模拟中使用的物质成分[8]Table 1 Materials used in Monte-Carlo simulation[8].

2.2参数计算

在计算过程中使用F5卡计算空气比释动能，使用F6卡计算吸收剂量。其中均是在假设带电粒子平衡的情况下，用比释动能来近似吸收剂量。本工作中计算所得参数，均只适合125I和103Pd放射性活度比为1:1的情况下的剂量率计算。

2.2.1 Λ的计算

计算125I-103Pd复合源的空气比释动能强度。建立半径为30 cm的球体，球体里为真空。先将单一含有125I的种子源放入球心，在种子源垂直平分线方向，布置距离种子源几何中心1.0、5.0、10.0、12.0、14.0、16.0、18.0和20.0 cm计数点。可以得到单一含有125I的种子源产生的空气比释动能，用同样的方法(只是源的参数不同)，可以得到103Pd产生的空气比释动能。

计算125I-103Pd复合源参考点处的吸收剂量。同样建立30 cm的球体，球体里充满液态水。先将单一含有125I的种子源放入球心，在通过种子源几何中心并且垂直于种子源长轴的平面上布置4个对称的参考计算点。将4个点的结果平均可以得到单一125I种子源的吸收剂量，同样的方法用于单一103Pd种子源。依据式(4)可以得Λ。

2.2.2 g(r)的计算

建立半径为30 cm的球体，球体内充满液态水。球心放置单一125I种子源，在种子源垂直平分线上，布置距离种子源几何中心计算点分别为±0.10、±0.15、±0.25、±0.30、±0.40、±0.50、±0.75、±1.00、±1.50、±2.00、±2.50、±3.00、±3.50、±4.00、±4.50、±5.00、±6.00、±7.00、±8.00、±9.00和±10.00 cm。将相应正负点处结果平均就可得单一125I种子源在该点产生的吸收剂量。用同样的方法计算单一103Pd种子源的吸收剂量。依据式(7)可得g(r)。

2.2.3 F(r,θ)的计算

建立半径为30 cm的球，里面充满液态水。球心放置单一125I的种子源，距离种子源几何中心0.5、1.0、2.0、3.0、4.0、5.0、6.0和7.0 cm处布置计数点。在每一计数点设置角度从0°到90°，间隔5°，共152个计算点。对单一103Pd种子源采用同样的计算方法，依据式(10)可以得到F(r,θ)。

3 参数计算结果和相关比较

3.1125I-103Pd复合源剂量率常数Λ

125I-103Pd复合源剂量常数Λ的计算结果见表2。

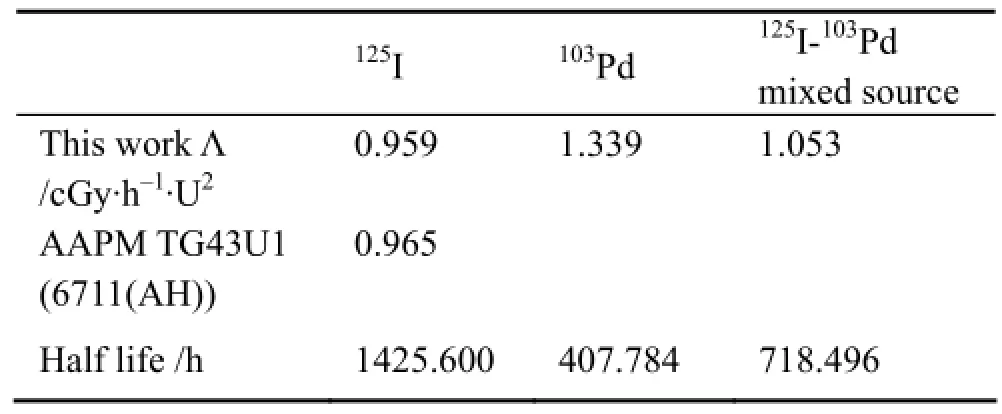
表2 剂量率常数ΛTable 2 Dose rate constant Λ.

由表2，其中单一源125I的剂量率常数与AAPM TG43U1中一种相类似的种子源6711(AH)的推荐值相差仅0.6093%。

3.2125I-103Pd复合源径向剂量函数g(r)

125I-103Pd复合源径向剂量函数g(r)的计算结果列于表3。

表3 径向剂量函数g(r)Table 3 Radial dose function g(r).

由表3，单一源125I与TG43U1推荐值最大相对误差为5.12%，而最小相对误差为0.15%。在表2中，单一源125I剂量率常数Λ与6711(AH)的推荐值相差仅0.6093%，可以证明本工作中所用的种子源几何模型和模拟过程的正确性。对表3中的125I-103Pd复合源数据进行拟合，可以得到125I-103Pd复合源径向剂量函数经验公式：

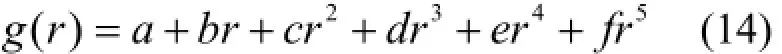
其中，a=1.23200；b=–1.54174×10–1；c=–1.10554×10–1；d=4.42442×10–2；e=–6.29650×10–3； f=3.18823×10–4； 残差平方和SSE=9.312×10–4，相关系数R=0.99982。此公式使用范围为r=0.1–10.0 cm。

3.3125I-103Pd复合源各向异性函数F(r,θ)

125I-103Pd复合源各向异性函数计算结果见表4。

由表4，可以拟合出125I-103Pd复合源各向异性函数的经验公式：

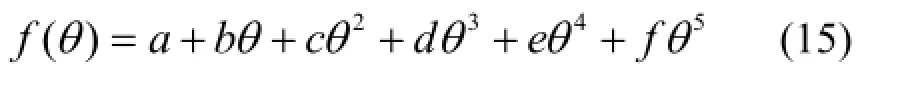
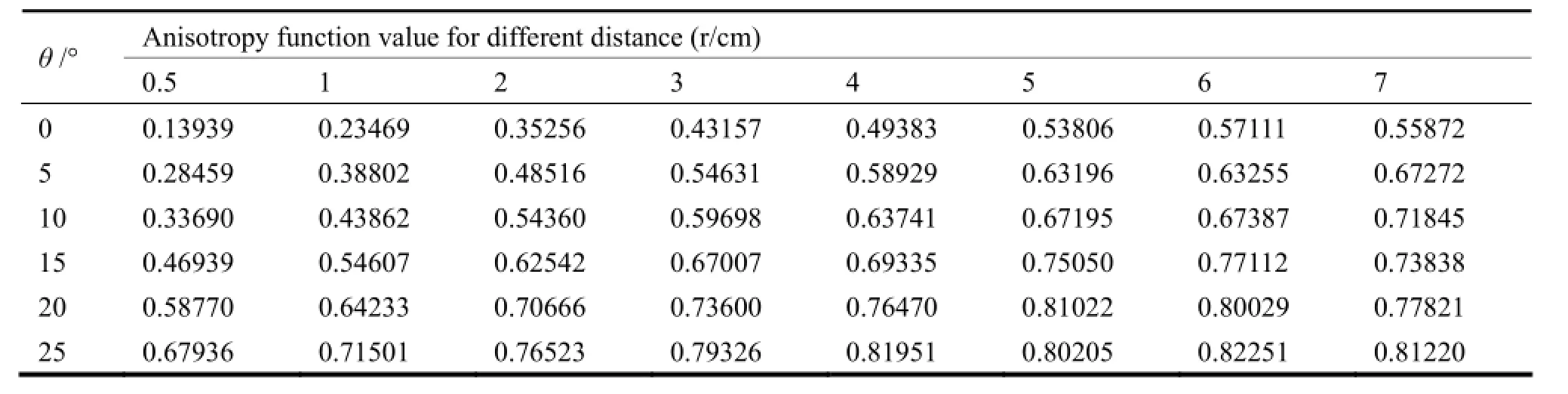
表4 125I-103Pd复合源各向异性函数F(r,θ)Table 4 Anisotropy function of the 125I-103Pd mixed source.

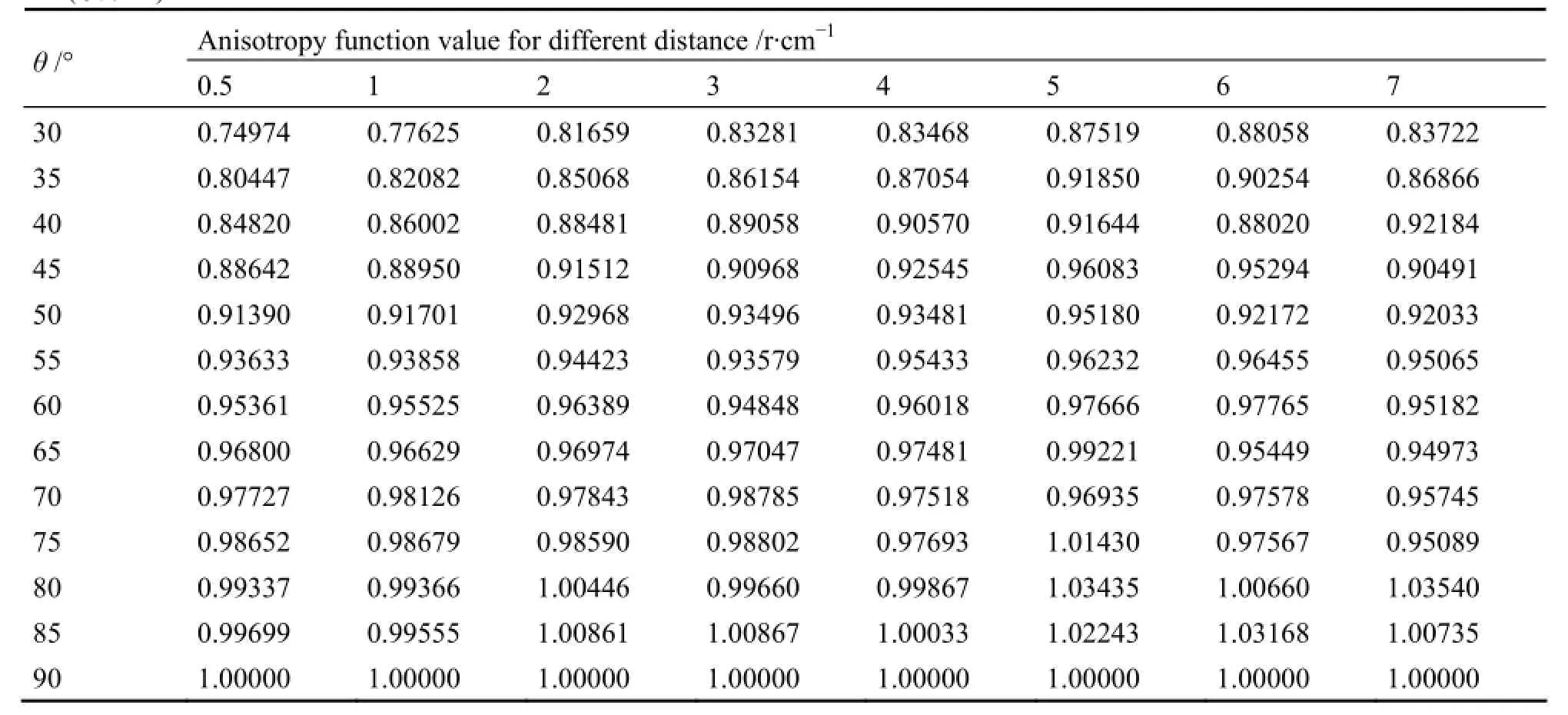
(续表4)

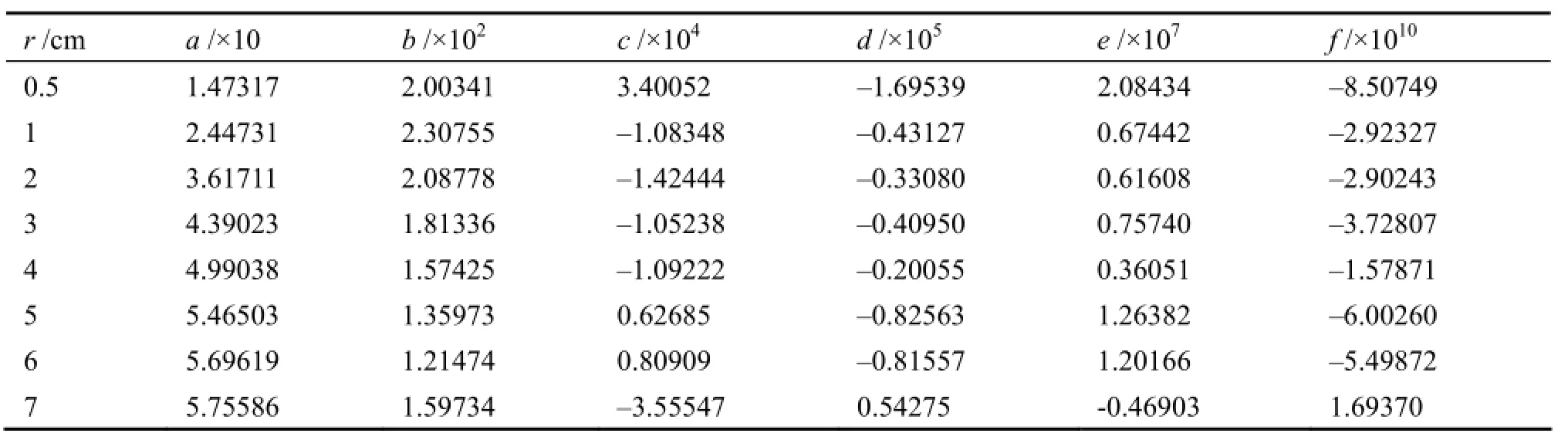
表5 各向异性函数的拟合结果Table 5 Fitting result for anisotropic function.

4 结语

本工作根据AAPM TG43U1中的相关规定，通过对单一种子源参数进行蒙特卡罗计算，得到单一源125I剂量率常数Λ与6711(AH)的推荐值相差仅0.6093%，径向剂量函数g(r)与TG43U1推荐值最大相对误差为5.12%，而最小相对误差为0.15%的结果。充分证明工作中使用的几何模型和物理参数的正确性，同时单一种子源参数的计算和复合种子源参数计算的过程极其相似。从而得到准确度较高的125I-103Pd复合源的各参数和经验公式，为临床治疗提供了必要的理论参考，使复合种子源的治疗达到更好的效果。

1 Meigooni A L I, Sharifeh A PH D, et al. TG-43 parameterization of a novel brachytherapy source designed with multi-radioisotopes[J]. Brachytherapy, 2008, 7(2): 171–172

2 George Fred Harder, Max Taghizadeh. Hybrid source containing multi-radionuclides for use in radiation therapy[P]. United states: US 2008/0249398 Al. 2008, 10, 09: 1–6

3 Rivard M J, Coutsey B M, Dewerd L A, et al. Update of AAPM task group No43 report: A revised AAPM protocol for brachytherapy dose calculations[J]. Medical Physics, 2004, 31: 633−674

4 Nath R, Anddrson L L, Luxton G, et al. Dosimetry of interstitial brachytherapy sources: recommendations of AAPM radiation therapy committee task group No43[J]. Medical Physics, 1995, 22: 209–234

5 孙亮, 李君利.125I短程治疗源剂量计算参数的蒙特卡罗确定[J]. 原子能科学技术, 2006, 40(6): 657–661

SUN Liang, LI Junli. Determination of dose calculation parameters of125I brachytherapy source with Monte-Carlo method[J]. Atomic Energy Science and Technology, 2006, 40(6): 657–661

6 李忠勇, 高慧波, 金小海, 等. 近距离治疗肿瘤的放射性粒子研究进展[J]. 同位素, 2011, 24(2): 118–123

LI Zhongyong, GAO Huibo, JIN Xiaohai, et al. Research progress in radioactive seed for brachytherapy[J]. Journal of Isotopes, 2011, 24(2): 118–123

7 X-5 Monte Carlo Team. MCNP-A General Monte Carlo

N-Particle Transport Code, Version 5, LA-UR-03-1987[R]. USA: LANL, 2003

8 Hubbell J H, Seltzer S M. Tables of X-ray mass attenuation coefficients and mass energy-absorption coefficients from 1 keV to 20 MeV for elements Z=1 to 92 and 48 additional substances of dosimetric interest, NISTER 5632[R]. Japan: NIST, 2004

CLC R312

Determination of dosimetric characteristics of125I-103Pd brachytherpy source with Monte-Carlo method

CAO Zhen1ZHAO Huali2XIE Qin3ZHANG Wenzai1FENG Gensheng1WANG Xiaojing1ZHANG Zijian4
1 (Atom High Tech Co. Ltd., Beijing 102413, China )
2 (China Nuclear Power Engineering Co., Ltd. Hebei Branch, Shijiazhuang 050019, China)
3 (School of the Nuclear Science and Technology, Lanzhou University, Lanzhou 730000, China)
4 (Department of Oncology, Xiangya Hospital, Central South University, Changsha 410008,China)

According to dose parameters calculation formula of seed source recommended by AAPM TG43U1,125I-103Pd seed source dose parameters calculation formula and a variety of radionuclides composite seed source of dose parameters calculation formula can be obtain. Dose rate constant, radial dose function and anisotropy function of125I-103Pd composite seed source are calculated by Monte-Carlo method, Empiric equations are obtained for radial dose function and anisotropy function by curve fitting. Comparisons with the relative data recommend by AAPM are performed. For the single source, the deviation of dose rate constant is 0.959 (cGy·h–1·U–1), and with 0.6093% from the AAPM.

Monte-Carlo method, Dosimetric characteristics,125I-103Pd, Empiric equation

R312

10.11889/j.0253-3219.2013.hjs.36.010203

曹振，男，1985年出生，硕士研究生，核技术及应用专业

2012-05-08，

2012-07-02