弹药协调器结构和位置控制动力学分析

郭宇飞，侯保林

(南京理工大学 机械工程学院，江苏 南京 210094)

0 引言

弹药协调器是坦克弹药自动装填系统的重要部件，它在一个固定位置，接受来自弹药仓的弹药，然后在控制器的作用下进行弹药协调，使得弹药轴线与待发射状态下的炮管轴线平行［1］。在坦克行进间连续射击过程中，一方面，由于火炮连续射击过程的剧烈振动，弹药协调器在工作过程中要承受强烈的外部扰动;另一方面，由于受到路面不平度的激励，弹药协调器的安装基础，即车体会产生随机振动，也对弹药协调器的工作稳定性产生影响［2］。

为了研究弹药协调器在安装基础扰动下的位置控制问题，本文以坦克弹药自动装填系统为背景，设计了一个按比例缩小的两自由度的弹药协调器模型，提出了一种针对这类存在不确定性外部扰动的拉格朗日系统的位置控制方案［3-4］。

1 弹药协调器的工作原理和动力学方程

弹药协调器安装在坦克底盘上，接收来自弹药仓的弹药，将弹药提升一定的高度，翻转相应的角度，使得弹药到达炮尾并与炮膛轴线同轴。在工作过程中，要求弹药协调器能够克服火炮射击和车体振动所产生的不确定扰动力，在2 s 内将弹药送到指定的位置。

图1为弹药协调器的工作原理图。弹药协调器由支架、升降部分与回转部分组成，采用链传动来实现弹药的升降动作。主动链轮与从动链轮在同一铅垂面内，主动链轮在下，从动链轮在上。主动链轮由电机、减速器与联轴器驱动，在链条的一边采用张紧轮来保证链传动能力。链条的另一边安装的回转部分可以沿着支架上的导轨上下滑动。回转部分包括电机、两个减速器与弹药接收机械臂。机械臂可以任意角度回转。采用左右对称的链传动结构来保证其工作稳定性，如图2所示。

图1 弹药协调器的工作原理Fig.1 The working principle of ammunition coordinator

图2 弹药协调器的虚拟样机模型Fig.2 The virtual prototype model of ammunition coordinator

将弹药协调器简化为在平面内运动的动力学模型，如图3所示。其中，XOY 为笛卡尔坐标系;B1为安装基础，B2为升降部分，B3为回转部分;O1、O2与O3分别为B1、B2与B3的质心;y1为安装基础的振动位移，y2为升降部分的位移，θ 为回转部分绕O2的回转角度，L 为O2与O3之间的距离。

图3 弹药协调器的简化动力学模型Fig.3 The simplified dynamics model of ammunition coordinator

以安装基础的振动位移、升降部分的位移与回转部分的回转角度为系统的广义坐标，由第二类Lagrange方程，可以得到弹药协调器的系统动力学方程

式中:m1、m2和m3分别为安装基础、升降部分和回转部分的等效质量;J 为回转部分的等效转动惯量;R 为安装基础受到的不确定振动力;F 为链传动作用在提升部分上的提升力;M1为作用在回转部分上的转矩;g 为重力加速度。

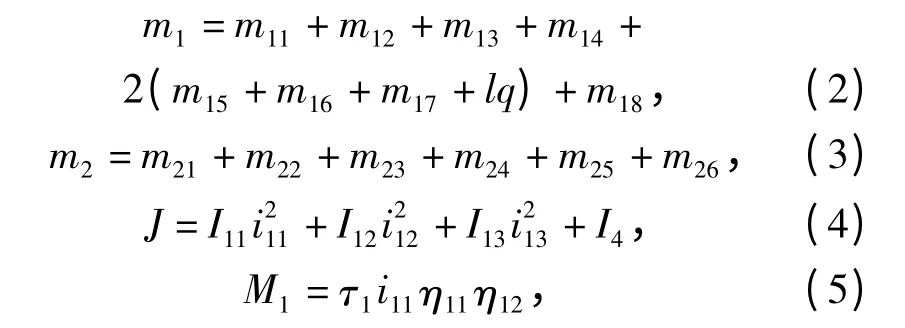
式中:m11、m12、m13与m14分别为支架、链传动电机、减速器与联轴器的质量;m15、m16、m17、与m18分别为主动链轮、从动链轮、张紧轮与主动链轮轴的质量;q 为单位长度链条的质量，l 为链长;m21、m22、m23、m24、m25与m26分别为升降部分左右安装板、回转电机、回转部分两减速器与回转机械臂的质量;I11、I12、I13与I4分别为回转电机、回转部分两减速器与回转机械臂的转动惯量;i11、i12与i13分别为回转电机、两减速器到回转机械臂的减速比;η11与η12分别为回转部分两减速器的传动效率;τ1为回转电机的驱动力矩。

回转电机采用他激直流电机驱动，其控制方程［6］为

式中:Ua1、Ia1分别为电压和电流;Rm1、Lm1分别为电枢的电阻和电感;φ1为磁通;k1为比例系数;Kt1为扭矩常数。

将链传动化为链节挠性可忽略不计的闭环多刚体动力学模型［7］。如图4所示，把紧边链条简化为一个直线运动的刚性块me1;以张紧轮为界，把松边链条简化为两个直线运动的刚性块me2、me3;与链轮啮合部分的链条分别简化为绕各自链轮轴定轴转动的刚体Ie1、Ie2、Ie3.

链传动为一单自由度多刚体系统，可以用单自由度多刚体系统的等效法来建立链传动部分的动力学方程。选择主动链轮轴为等效构件，有:

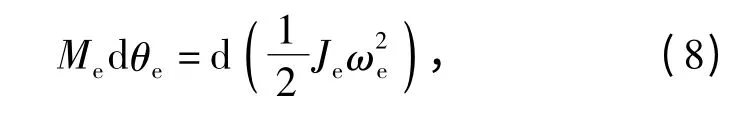
式中:θe为主动链轮的转角;为主动链轮的转速;Me为等效力矩。

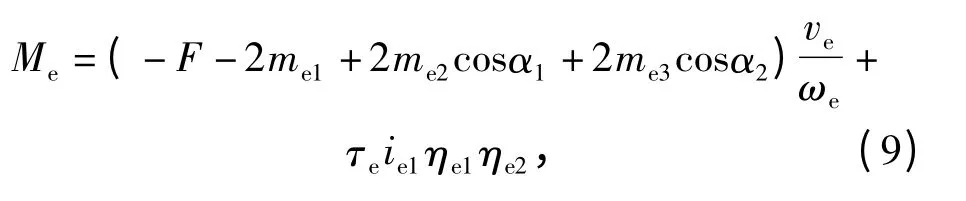
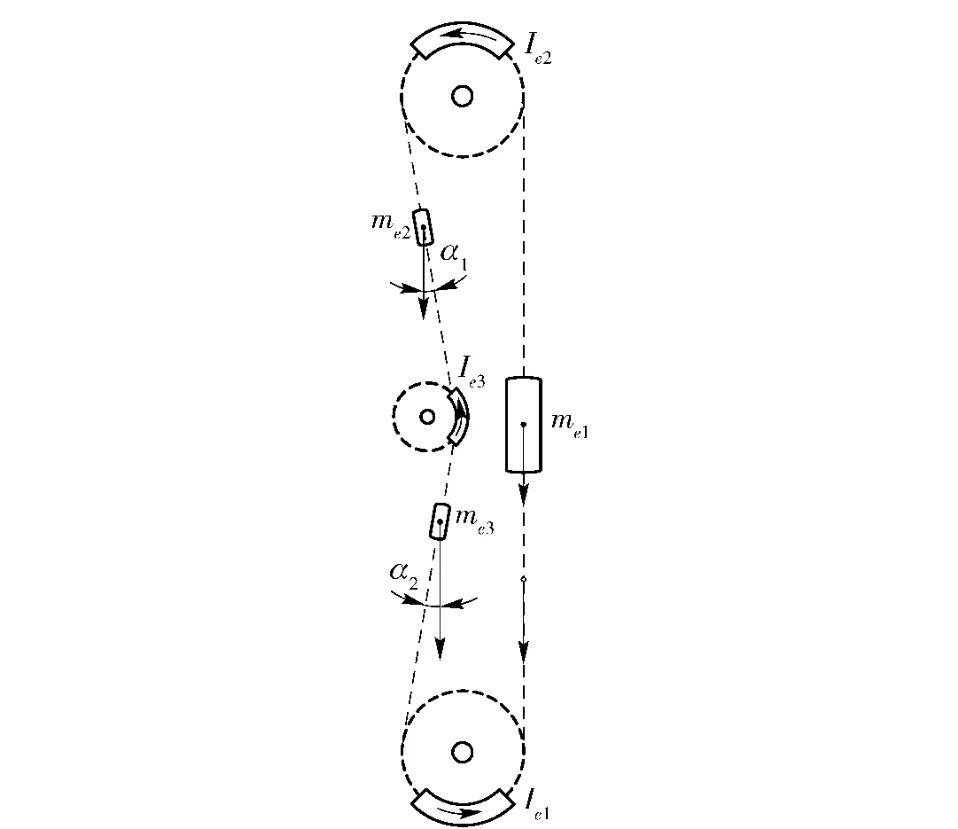
图4 链传动动力学分析Fig.4 The dynamics analysis of chain drive system

式中:ve为链条的速度;α1与α2分别为相应刚体的重力与速度的夹角;τe为链传动中电机的力矩;ie1为电机到链轮的减速比;ηe1与ηe2分别为减速器与联轴器的传动效率。

等效转动惯量

式中:mj包括me1、me2与me3;Jα、Jβ与Jγ分别为主动链轮轴、从动链轮轴与张紧轮转轴上的所有转动惯量;ωe1与ωe2分别为从动链轮与张紧轮的转速;Id1、Id2与Id3分别为链传动中电机、减速器与联轴器的转动惯量;ie2为链传动中减速器的减速比。

链传动电机也采用他激直流电机驱动，其控制方程［6］为

式中:Uae、Iae分别为电压和电流;Rme、Lme分别为电枢的电阻和电感;φe为磁通;ke为比例系数;Kte为扭矩常数。

(1)式～(12)式构成了弹药协调器的动力学方程组，这是一组非线性方程。

2 位置控制器系统动力学计算

考虑系统的拉格朗日形式的动力方程为

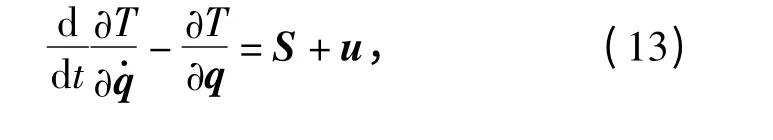
为系统动能，〈，〉为两个向量的内积，A(q)为系统动能的一个正定对称矩阵，其特征值总处于一定的范围［m，M］内，0 ＜m ＜M，即

式中:z 为A(q)的特征向量;|z|为向量的模。A(q)的偏微分的大小总是有界，即

假设广义控制力与外部扰动力大小有界，即

U 与S0之间满足关系

式中:(q0，)为系统的初始状态;V(q0，)为系统的Lyapunov 函数在初始状态时的值。则存在控制力u，可以在有限的时间内，把系统由一定的初始状态驱动到指定的终点状态。由于任意的状态都可以通过适当的坐标变换转换为原点状态，不失一般性，这里指定终点状态为广义坐标的原点。

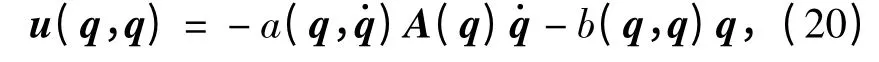
其中，

q2+为系统状态与原点之间的距离。(21)式、(22)式给出了隐式函数

将(21)式带入(22)式，并定义

则有

定义

定理1 对于满足q2+＞0 的任意q 与，总有|μ|≤σλ，并且方程(25)总存在唯一正实根。

定理2 在领域R2n|{(0，0)}内，满足(21)式与(22)式的连续可微函数a(q，)、b(q，)与V(q，)总存在。

定理3 在初始时刻t0给定δ(t0)＞0，则有

给定初始状态(q0，)，可以通过牛顿迭代法求解(25)式得到该时刻V(q0，;t0)的值，继而通过求解(20)式得到广义控制力u 的值;接着根据已知的广义控制力u，采用龙格库塔法单步迭代求解(13)式，便可得到下一时刻的系统状态(qt).如此反复交叉迭代，直到得到满足要求的控制精度时终止迭代。如图5所示。

图5 数值求解过程Fig.5 Numerical solution process

3 数值仿真

对于由(1)式描述的弹药协调器，可以把方程组中安装基础部分提取出来看作不确定性外部扰动，有

式中:u1=F;u2=M1;

则有

选择各仿真参数m2=8.6 kg，m3=3.6 kg，J =1.6 kg·m2，L =0.5 m，U =600，S0=250;经计算有M=12.52 kg·m2，m =2.18 kg·m2，C =3.对安装基础施加幅值有界的随机振动加速度在0～10 m/s2之间随机选取，每步迭代选择一次，如图6所示，则得到如图7和图8所示的外部扰动力S1、S2.选择系统的初始状态为y2=1 m=0 m/s，θ=π/4 rad，=0 rad/s，在MATLAB 中进行数值仿真，当系统状态与状态原点之间的距离小于0.01 时，即时，终止迭代。

仿真结果如图9～图15 所示，图9和图10 为升降部分的位移与速度;图11 和图12 为回转部分的角位移与角速度;图13 和图14 分别为升降部分的广义控制力与回转部分的广义控制力矩;图15 为Lyapunov 函数值随时间的变化。可以看出，在不到2 s 的时间内，系统在控制器的驱动下由一定的初始状态运动到了指定的终点状态;控制力始终处在给定的范围内;Lyapunov 函数值最终趋向于0.Lyapunov 函数值非单调递减的原因是，为了满足工程需要U 选择了较小的值，从而导致约束条件(19)式无法满足。但是，所设计的位置控制器仍然能够克服不确定性外部随机扰动的影响，把系统由一定的初始状态驱动到指定的终点状态，具有良好的鲁棒性能。

图6 基础振动加速度Fig.6 The vibration acceleration of base

图7 升降部分所受到的扰动Fig.7 The disturbance on lifting part

图8 回转部分所受到的扰动Fig.8 The disturbance on rotating part

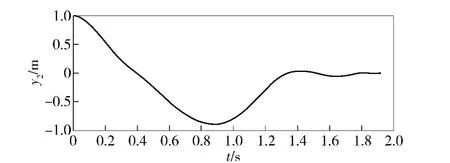
图9 升降部分的位移Fig.9 The displacement of lifting part

图10 升降部分的速度Fig.10 The velocity of lifting part

图11 回转部分的角位移Fig.11 The angular displacement of rotating part

图12 回转部分的角速度Fig.12 The angular velocity of rotating part

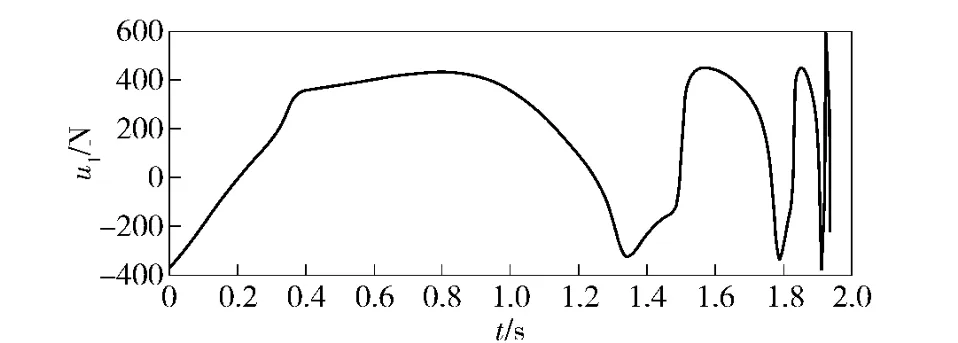
图13 升降部分的控制力Fig.13 The control force of lifting part

4 结论

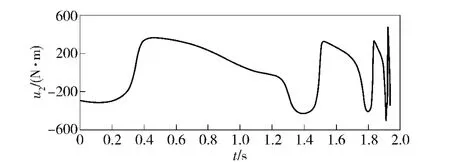
图14 回转部分的控制力矩Fig.14 The control torque of rotating part

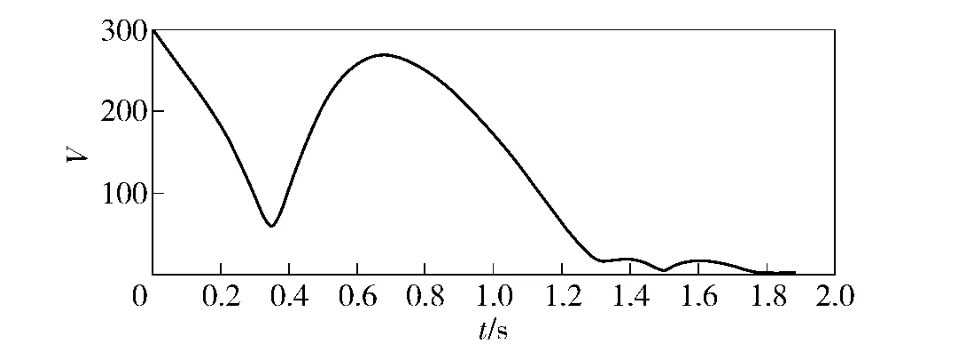
图15 Lyapunov 函数Fig.15 Lyapunov function

1)提出一种两自由度弹药协调器结构方案，结合一种基于给定隐式Lyapunov 函数的非线性位置控制算法可以实现存在安装基础振动情况下弹药的准确协调定位。

2)将第二类Lagrange 形式的弹药协调器动力学方程中的基础振动部分提取出来看作外部扰动，得到比原模型少一个自由度的不确定动力系统，为该类考虑基础随机振动的系统的建模分析提供了一种有效的方法。

3)采用一种基于隐式Lyapunov 函数的连续反馈控制算法设计了的弹药协调器的位置控制器，消除了基础随机振动所带来的非线性影响，使弹药协调器在有限的时间内由指定的初始状态运动到原点状态。

4)仿真结果验证了该控制算法的有效性、强鲁棒性。

References)

［1］ 侯保林，樵军谋，韩宏潮.弹丸传输机械臂结构与控制的综合设计方法［J］.兵工学报，2006，27(5):788 -791.HOU Bao-lin，QIAO Jun-mou，HAN Hong-chao.Integration design method of structure and control for a shell transfer arm［J］.Acta Armamentarii，2006，27(5):788 - 791.(in Chinese)

［2］ 程刚，张相炎，董志强，等.轮式自行高炮行进间射击稳定性仿真研究［J］.兵工学报，2010，31(2):149 -153.CHENG Gang，ZHANG Xiang-yan，DONG Zhi-qiang，et al.Simulation research on the stability of firing on-the move for wheeled self-propelled anti-aircraft gun［J］.Acta Armamentarii，2010，31(2):149 -153.(in Chinese)

［3］ Anan’yevskii I M.Continuous feedback control of perturbed mechanical systems［J］.Journal of Applied Mathematics and Mechanics，2003，67(2):143 -156.

［4］ Chernousko F L，Ananievski I M，Reshmin S A.Control of nonlinear dynamical systems:methods and applications ［M］.Berlin:Springer，2008:213 -229.

［5］ 成大先.机械设计手册:机械传动［M］.北京:化学工业出版社，2004:12 -123.CHENG Da-xian.Mechanical design handbook:mechanical transmisson［M］.Beijing:Chemical Industry Press，2004:12 - 123.(in Chinese)

［6］ 辜承林.机电动力系统分析［M］.武汉:华中科技大学出版社，1998:68 -70.GU Cheng-lin.Analysis of electrical machine dynamic［M］.Wuhan:Huazhong University of Science and Technology Press，1998:68 -70.(in Chinese)

［7］ 刘晓论，荣长发，张格，等.高速滚子链传动动力学分析［J］.农业机械学报，1998，29:177 -181.LIU Xiao-lun，RONG Chang-fa，ZHANG Ge，et al.Dynamic analysis of roller chain drives at high speed［J］.Transactions of the Chinese for Agricultural Machinery，1998，29:177 - 181.(in Chinese)