结合罚函数与序列二次规划的lp 范数优化方法

马 聪，刘 哲，甄小仙

西北工业大学 理学院，西安710129

1 引言

信号采样是联系模拟信源和数字信息的桥梁。人们对信息的巨量需求造成了信号采样、传输和存储的巨大压力。如何缓解这种压力又能有效提取承载在信号中的有用信息是信号与信息处理中急需解决的问题之一。而近年来出现的压缩感知理论（Compressed Sensing，CS）[1-2]提供了解决办法，它突破了传统的奈奎斯特采样定律的限制，是一种可以同时完成采样和压缩的新型信号处理理论，其核心思想是：在某个变换域是稀疏的或者可压缩的信号，可以用一个与变换基不相关的观测矩阵将变换所得高维信号投影到一个低维空间上，然后通过求解一个优化问题从这些少量的投影中以高概率重构出来。

在CS 理论中，信号的重构基于范数优化理论展开，数学意义上来讲就是求解l0范数优化问题，但该问题属于非凸优化问题[2]，是NP 难的。文献[3]证明了可以用l1范数代替l0范数求解得到同等的解，但该方法还需要较多的观测样本。文献[4]构造了lp(0 ＜p ＜1)范数实现算法，实验性地证明了基于lp(0 ＜p ＜1)范数的优化算法在重构信号效果及算法可靠性方面优于l0范数优化和l1范数优化。文献[5]从几何学角度对不同范数的物理模型作出了解释，并证明了lp范数在信号重构方面的优越性。

本文以非线性最优化为方向研究lp范数优化，提出了结合罚函数法和序列二次规划方法（SQP）的lp范数优化算法，实现了lp范数最优化意义下CS 理论信号重构。

2 基于lp 范数优化的信号重构

设一个N 维有限长实信号x ∈RN，Φ 是一个M×N(M ≪N)维的观测矩阵，观测值y=Φx 是一个M 维向量。在CS 理论框架下，原信号x 可以利用观测向量y 通过求解如下问题得到重构：

其中‖·‖0表示向量中非零元素的个数，也称为l0范数，但是该问题计算数值极不稳定，很难利用现有的优化方法有效求解。但是在满足变换矩阵和观测矩阵不相关的前提下，求解一个更加简单的l1范数优化问题代替l0范数优化可以得到同等的解[3]，即

这样的改变将一个难以解决的非凸优化问题转化成了一个凸优化问题，能够方便地简化为线性规划进行求解。但l1范数优化还存在计算复杂度较高、需要观测样本较多和数据间有较大冗余性等缺陷。为了进一步改进重构算法性能，直接最小化原信号的非凸lp(0 ＜p ＜1)范数[4]，即

能够很好地从数学原理上逼近信号重构的原问题，不仅可以在一定程度上减少数据之间的冗余，而且大大减少准确重构原信号所需要的观测数量。虽然lp范数优化的研究成果很少，但是在信号重构方面已经表现出了巨大的优势，有效提高了基于CS 理论的信号重构效果。

目前，最典型的lp(0 ＜p ＜1)范数实现算法是迭代加权最小二乘（IRLS）法[6]，文献[7]利用该算法从少量线性观测中有效地重构原矩阵信号，并证明了任意由观测向量唯一确定的稀疏信号均可以通过lp范数优化方法精确重构。在IRLS 算法基础上，Rick Chartrand[8]提出了更为高效的参数规则化的IRLS 算法：

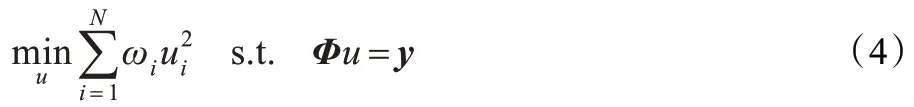
采用古典欧拉-拉格朗日乘子法求解式（4）得到其解：

Qn是一个对角矩阵，其元素为1/ωi。在迭代过程中，通过对参数ε 规则化处理，提高了对稀疏信号的重构能力。

3 结合罚函数与序列二次规划的lp 范数优化算法

3.1 基于罚函数的lp 范数优化问题求解

罚函数法[9]是一种求解非线性规划问题的数值解法，它是将有约束的最优化问题通过罚因子的选择变为一系列求罚函数的无约束极小值问题。

以最小化lp范数为目标，文献[10]从罚函数优化角度提出了一种lp范数迭代重构算法。令目标函数为：f(x)=，约束条件转化为：Φx-y=0，罚函数定义为：

通过增大罚因子，迫使迭代值进入可行域并逼近最优值。上式最优解的迭代计算式为：

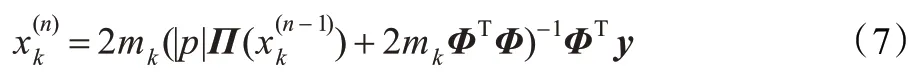
其中，mk为罚因子，Π(xk)=diag(|xk(i)p-2|) 。通过对目标函数进行非约束转换和梯度修正，实现了对稀疏信号的精确重构。但是随着罚因子的增大，会导致约束条件变得很坏，从式（6）也可以看出，当mk→∞时，为了求出最优解，必然要求Φx-y →0，这就给后期的计算带来巨大的压力，使得数值性能不好。因此在重构稀疏度较高的信号时，该方法不够稳定且计算复杂度较高。

3.2 基于SQP 方法的lp 范数重构算法

序列二次规划方法（Sequential Quadratic Programming，SQP）[11-12]是求解无约束最优化问题的牛顿法和拟牛顿法对约束最优化问题的推广，其基本思想是每一步迭代通过求解一个二次规划子问题来确定一个下降方向，以减少价值函数来取得步长，重复步骤直到求得原问题的解。

以非线性最优化为方向实现lp范数的优化，采用SQP方法来求解lp范数：

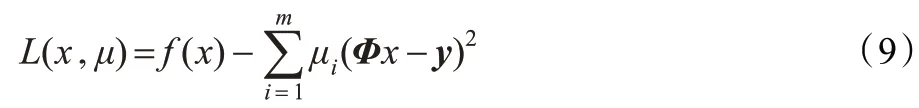
由问题式（9）取极小值的KT 条件[13]得到：

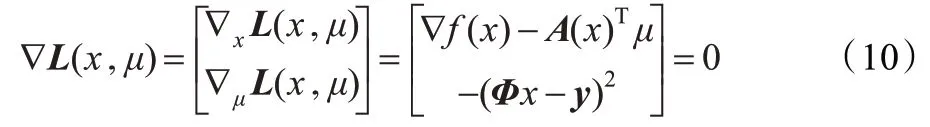
其中∇f(x)=|p|diag(|x|p-2)x ，A(x)是约束函数(Φx-y)2的雅可比矩阵，采用牛顿法求解式（9），对于给定的点zk=(xk,μk)，牛顿法迭代格式为：

这里pk=(dk,vk)满足线性方程组：

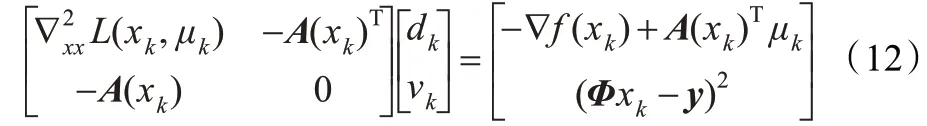
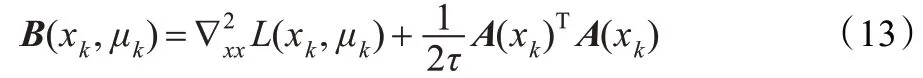
其中τ ＞0 且充分小，式（12）等价为：

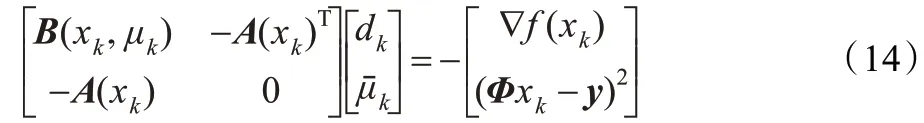
上式可以方便地利用二次规划问题求解。

3.3 结合罚函数与SQP 的lp 范数优化方法

SQP 方法因具有很好的收敛性被广泛应用于求解约束最优化问题，定理1[11]则从理论上阐明了该方法的收敛性。

定理1 假设目标函数f(x) 与约束函数hj(x) 二阶可微，问题式（8）的最优解x*存在，雅可比矩阵A(x*)满秩，存在μ*使得式（9）成立，如果初始点x0充分接近x*，则每次迭代二次规划子问题的最优解存在，迭代序列{xk}收敛于x*，且收敛速度是二次的。

罚函数法简单直观，随着参数mk的增大，可以迫使初始点不断向最优解靠近，但是当参数mk→∞时会使得迭代计算后期的数值性能不好。

考虑到以上两种方法的特点，提出结合罚函数与序列二次规划的lp范数优化算法（简记为P-SQP 算法），首先利用罚函数法对初始点进行预估计，在这个过程中，不需要过多增大罚因子，仅是利用罚函数法做一个初步的计算，迫使初始点进入可行域，然后采用SQP 方法求解计算。因为上一步计算已经保证了矩阵的正定性，根据定理1 利用SQP 方法二次收敛的优点进行后续计算可以快速求得原问题的最优解。因此，P-SQP 算法结合了罚函数与SQP 两种方法的优点并克服了各自的不足，可以有效实现稀疏信号的重构。

P-SQP 具体算法步骤如下：

步骤1选取初值x0∈Rn，μ0∈Rm，ρ,γ ∈(0,1)，0 ＜ε ≪1，误差e，令k=0。

步骤2将x0代入式（7）求解，当迭代值x满足‖Φx-y‖2＜e 时停止计算，令x0=x。

步骤3计算‖ ∇L(xk,μk) ‖，若‖ ∇L(xk,μk) ‖≤ε ，停止计算，否则转步骤4。

步骤4求解式（14），得dk和，并置vk=-μk-

步骤5令mk是使下式成立的最小非负整数m：

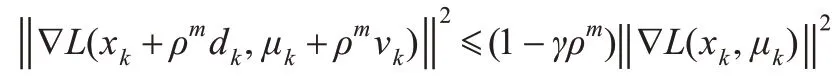
令αk=ρmk。

步骤6令xk+1=xk+αkdk,μk+1=μk+αkvk，k=k+1 返回步骤3。

下面通过实验将P-SQP 算法与IRLS 算法[8]和文献[10]算法进行比较分析，证明P-SQP 算法在一定程度上提升了对稀疏信号的重构能力。

4 实验结果及分析

第一个实验是研究初值选取对P-SQP 算法收敛性的影响。实验信号x 选取长度为256 的稀疏信号，观测矩阵Φ 取100×256 的独立同分布高斯矩阵，信号x 的稀疏度K依次为K=30,32,…,70，对每一个K 值，随机生成100 个高斯随机稀疏信号并采用P-SQP 算法做信号重构实验（以下实验中，当最优解满足‖-x‖2＜10-3时视为精确重构）。算法第一步是用罚函数法对初始值进行预估计，使得迭代初值x0满足‖ Φx0-y‖2＜e，误差e 的大小反映了x0和原信号x 的接近程度。图1 给出了对于3 个不同大小的e 值，P-SQP 算法得出的精确重构概率曲线。

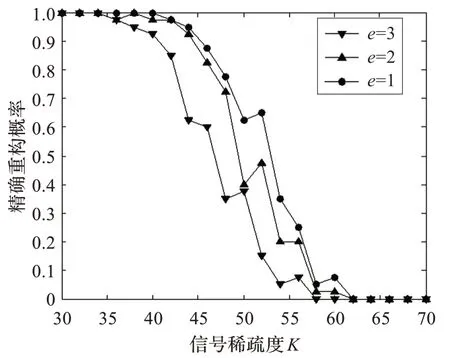
图1 不同e 值对应的重构概率图

可以看出，e 值越小，即x0和x 越接近，P-SQP算法对信号的精确重构概率越高，同时也证明了本文提出的P-SQP算法是有效可行的。

第二个实验是比较IRLS 算法，文献[10]算法，P-SQP 算法对稀疏信号的精确重构效率及平均计算时间，实验信号及观测矩阵的选取同实验1，图2 和图3 分别给出了随着信号稀疏度的增加，三种算法对信号x 的重构概率曲线和平均计算时间曲线。

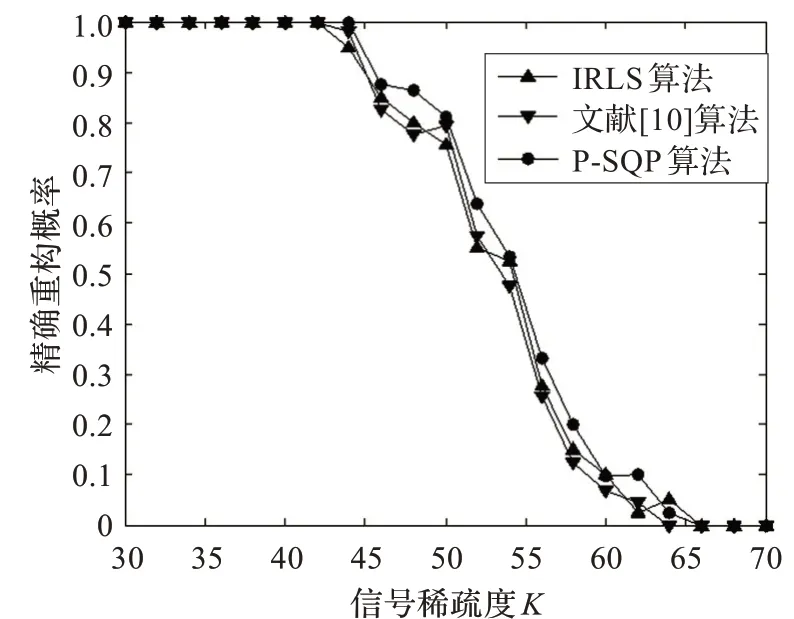
图2 三种算法精确重构信号概率图

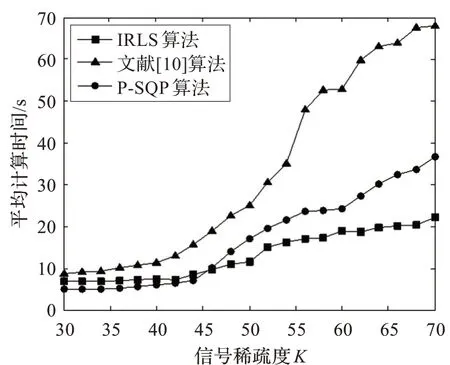
图3 三种算法重构信号平均计算时间曲线图

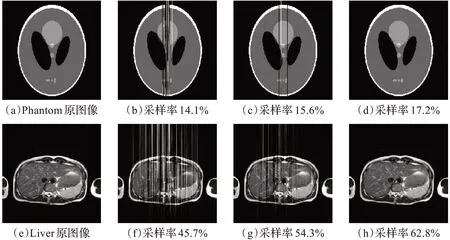
图4 P-SQP 算法重构图像

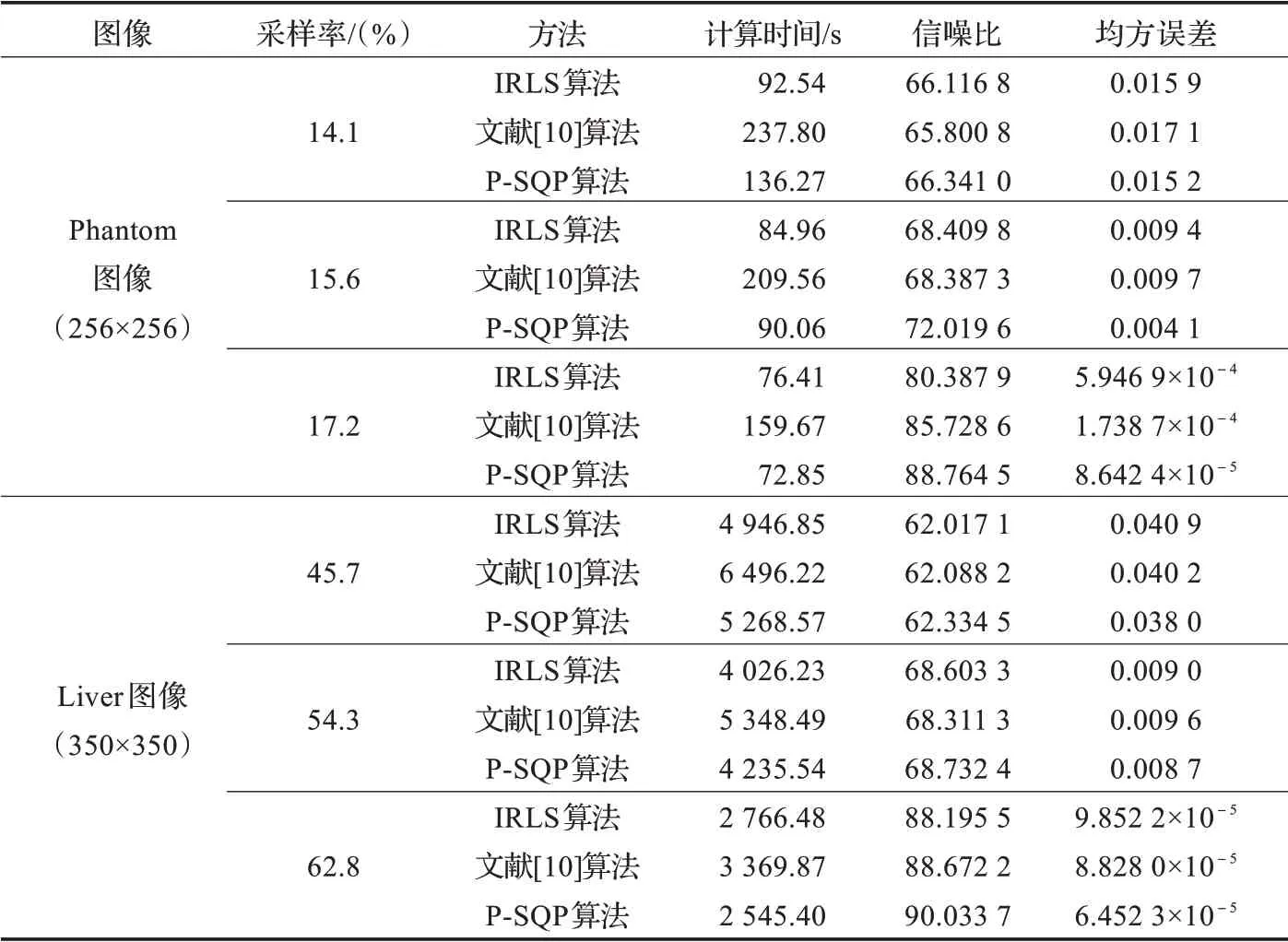
表1 三种算法重构图像结果

从图2 和图3 可以看出，对于相同的稀疏信号，P-SQP算法的重构概率是最高的；同时，在信号稀疏度较低情况下，P-SQP 算法的收敛速度最快，计算时间是最少的。证明了P-SQP 算法充分结合了罚函数与SQP 两种方法的优点，能够有效地重构稀疏信号。

第三个实验是研究P-SQP算法对稀疏图像的重构效果，首先对图像施用水平梯度稀疏化算子得到稀疏图像x1，采用P-SQP 算法对其进行采样重构得到稀疏重构图像x2，然后利用水平梯度逆算子得到重构图像x。

选取大小为256×256 的Phantom 图像和350×350 的MRI-Liver 图像作为实验图像，其水平梯度图像的列最大稀疏度分别为K1=14，K2=148。采用P-SQP 方法对图像进行重构，实验结果如图4 所示。

对于Phantom 图像，当采样率分别为14.1%、15.6%时，重构图像与原图像的信噪比分别为66.341 0、72.019 6，均方误差分别为0.015 2、0.004 1；而当采样率提高到17.2%时，重构图像与原图像的信噪比为88.764 5，均方误差为8.642 4×10-5，达到了近似精确重构。对稀疏度较大的MRILiver 图像进行重构，随着采样率的提高也得到了同样的实验结果。证明了本文算法可以有效重构稀疏图像。

为比较IRLS 算法，文献[10]算法，P-SQP 算法对稀疏图像的重构效果，分别取不同的观测数进行采样，表1 给出了三种算法在不同采样率下重构图像的客观结果。

从表1 可以看出，当达到一定的采样率时，对于不同的稀疏图像，三种算法均可以实现精确重构。在相同采样率下，P-SQP 算法得到的重构图像与原图像的信噪比更高，均方误差也更小。并且随着采样率提高，可以实现对图像的精确重构时，P-SQP 算法的计算时间是最少的。进一步验证了本文算法的可行性与有效性。

5 结束语

lp范数问题是信号优化重构的一个新的方向，对它的研究将推动压缩感知理论在压缩方面的应用，但是lp范数属于非凸函数优化问题，目前的研究成果不是很多，很多数学问题还需要进一步解决。本文沿着非线性最优化方向，采用典型的约束优化方法来求解lp(0 ＜p ＜1) 范数优化问题。提出了结合罚函数和序列二次规划方法的P-SQP 优化算法，并进行了实验分析，证明了该算法是一种有效的lp范数求解算法。如何选取初值或对其预估计使其进入可行域，使得该算法更具有应用性还需进一步研究。

[1] Donoho D.Compressed sensing[J].IEEE Trans on Information Theory，2006，52（4）：1289-1306.

[2] Candès E.Compressive sampling[C]//International Congress of Mathematicians，Madrid，Spain，2006：1433-1452.

[3] Chen S S，Donoho D L，Saunders M A.Atomic decomposition by basis pursuit[J].SIAM Review，2001，43（1）：129-159.[4] Chartrand R.Exact reconstruction of sparse signals via nonconvex minimization[J].IEEE Signal Process Lett，2007，14：707-710.

[5] Baraniuk R.A lecture on compressive sensing[J].IEEE Signal Processing Magazine，2007，24（4）：118-121.

[6] Rao B D，Kreutz-Delgado K.An affine scaling methodology for best basis selection[J].IEEE Trans on Signal Process，1999，47：187-200.

[7] Fornasier M，Rauhut H，Ward R.Low-rank matrix recovery via iteratively reweighted least squares minimization[J].Communications on Pure and Applied Mathematics，2010，1：1-38.

[8] Chartrand R，Yin W.Iteratively reweighted algorithms for compressive sensing[C]//Proceedings of the 33rd International Conference on Acoustics，Speech，and Signal Processing（ICASSP），2008.

[9] 傅英定，成孝予，唐应辉.最优化理论与方法[M].北京：国防工业出版社，2008.

[10] 刘哲，杨扬.一种新的基于压缩感知理论的稀疏信号重构算法[J].光电子激光，2011，22（2）.

[11] 孙文瑜，徐成贤，朱德通.最优化方法[M].北京：高等教育出版社，2010.

[12] Gill P E，Wong E.Sequential quadratic programming methods，Technical Report NA-10-03[R].UCSD Department of Mathematics，2010.

[13] Jeyakumar V，Srisatkunarajah S.Geometric conditions for Kuhn-Tucker sufficiency of global optimality in mathematical programming[J].European Journal of Operational Research，2009，194：363-367.