薄覆冰导线气动力特性风洞试验研究

李海若，郭海超，谢强

(1.同济大学土木工程学院，上海市200092;2.机械工业第六设计研究院有限公司，郑州市450001)

0 引言

2009年末、2010年初，湖南省长沙、湘潭等地区有10多条线路因舞动而跳闸［1］;2010年末江西大部分地区遭受到了雨雪灾害，对电网系统造成影响。舞动发生地已经由传统的中部南移到湖南、江西等地区。输电线路覆冰已经成为电力防灾的重点，也是一项难题［2］。

有关舞动的历史记录和研究由来已久，国外从上世纪30年代就开始注意到舞动现象，许多研究者对这个难题作了深入的探讨和分析。Den Hartog首次提出了垂直舞动理论模型，即建立了导线质点沿垂直线路方向的运动方程，并通过该方程阻尼项是否为负来判定系统的稳定性［3］。Nigol提出了扭转舞动理论模型，即建立了导线质点绕线路方向扭转的运动方程，通过该方程的阻尼项是否为负来判断系统是否稳定［4-5］。Richardson用风荷载作用在导线上产生的升力所做的功等于阻力所做的功来解释舞动的一些现象［6-7］。Yu P用惯性耦合失稳理论来解释覆冰导线的驰振［8］，之后Yu P与Desai又提出了三自由度驰振理论［9］。何锃、赵高煜提出了分裂导线舞动分析的动力学模型，并对提出的模型进行了分析计算［10-11］。蒋兴良等从导线覆冰机理方面入手提出多种方法来减少或防止导线覆冰［12-13］。顾明教授对多种类型覆冰截面进行试验研究，得到了多种覆冰截面形式的气动力系数［14-15］。

本文在前人研究成果的基础上，根据2009年底在湖南长沙220 kV输电线路覆冰舞动现场的观测与调查，选用薄准椭圆形(也称新月形)覆冰导线模型进行了风洞试验研究，得到均匀流场和紊流场中薄覆冰导线截面气动力系数随风向角变化规律，进而分析覆冰导线的稳定性。

1 试验模型及风洞试验概况

导线覆冰首先在迎风面上生长，在风向比较稳定的情况下，覆冰就会在迎风面上积累，当迎风面覆冰达到一定厚度时，导线发生扭转，迎风面积会增大，覆冰就会进一步扩大变厚，最终在导线上形成准椭圆形覆冰、扇形覆冰和其他种类的覆冰［14］。本文根据2009年底湖南长沙220 kV输电线路覆冰舞动现场调查结果，选用最典型的准椭圆形覆冰导线作为试验对象，设计了3种覆冰厚度进行了风洞试验研究。选取的导线原型为LGJ-240/55(外径为22.4 mm)。

实验采用六分量高频天平对覆冰导线的刚性节段模型的气动力进行测量。模型有效高度为0.5 m，采用高频测力天平进行测力时，要求整个模型所受到的力不能超过天平6个分量的量程，并且模型应具有较高的刚度。本实验用铝管来模拟导线的内芯，用熟料来模拟导线覆冰面和导线上的螺纹，覆冰导线模型的形状如图1所示。

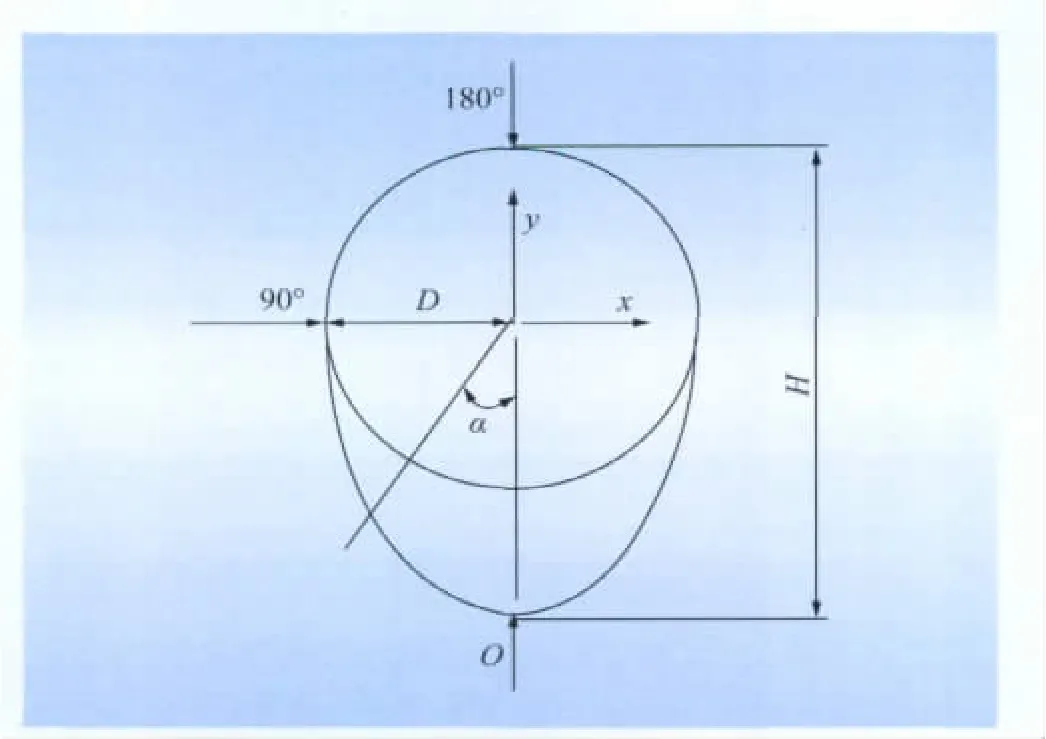
图1 覆冰导线形状及试验工况Fig.1 Experiment cases and ice shapes

根据不同的覆冰厚度来区分模型，A、B、C模型覆冰厚度如表1所示，规范中覆冰厚度≤10 mm的作轻度覆冰考虑，模型A、B、C即为薄覆冰的状况。从统计资料可以看出［2］，在发生舞动时，现场的风速为8～15 m/s，在试验时取10 m/s。试验采样频率为1 000 Hz，采样时间为2 min，采样点为12万点。试验中，风向的变化范围为0°～160°，增量为10°。根据顾明教授风洞试验结果及分析在170°和180°这2个比较不常见的风向角下，导线不会发生舞动［14］，为节省试验时间，本文不对在这2个风向角下模型的气动力进行测试。模型A、B、C这3种不同厚度覆冰截面形式的导线都是按照上述工况进行测力分析。

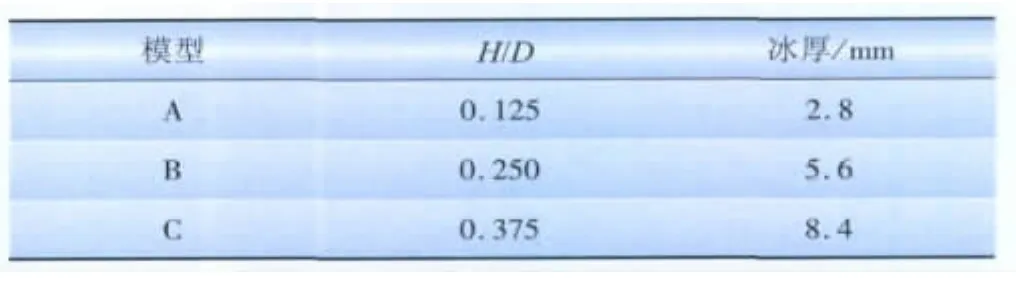
表1 模型的覆冰厚度Tab.1 Ice thickness of models

试验风速是用皮托管和扫描阀来测量和监控的，模拟风场的调试和测定采用美国Scanivalve扫描阀公司生产的DSM3000型电子式压力扫描阀系统。该系统可以用来测量流场的平均风速、风速剖面、湍流度以及脉动风功率谱等数据。试验分别测试了在10%紊流场和均匀流场2种不同流场中模型A、B、C的平均气动力，并对它们进行对比分析。10%紊流强度是荷载规范对B类场地计算得到的［16］，这种紊流场的获得是通过在风洞中加栅格所得。

2 平均气动力特性分析

根据模型坐标体系(图1)建立覆冰导线气动力体系，x风向为顺风向，y为垂直风向方向(即横风向)，M的方向按照右手定则确定，在实验中转动模型，保持(0°～160°)x、y、M 的方向不变，力系数采用如下定义:

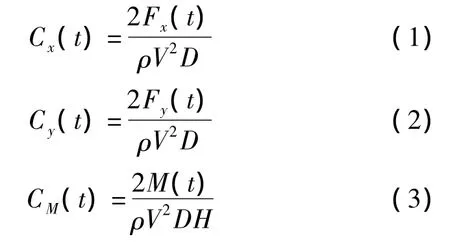
式中:Cx(t)、Cy(t)和 CM(t)，分别为 x、y向平均力系数和平均扭矩系数;Fx(t)、Fy(t)、M(t)分别为 x、y向平均力和平均扭矩;ρ、V、D、H分别为空气密度(本文取1.225 kg·m－3)、试验风速、导线参考直径、模型高度。

2.1 在均匀流场中A、B、C模型的气动力均值

A、B、C模型在均匀流场中的平均阻力系数、升力系数和扭矩系数分别如图2(a～c)所示。

图2 在均匀流场中模型力系数均值Fig.2 Average aerodynamic force coefficients of models in uniform flow field

从图2(a)可以看出A模型阻力系数均值的最大值在40°风向角处，值为0.913;最小值在0°风向角处，值为0.566。在0°～40°时，随迎风角变大阻力系数变大;在40°～90°时，阻力系数略微下降;在 90°～110°时，又有些许上升;从110°～160°时为下降趋势。升力系数的均值在20°风向角时达到最大，值为0.337;在20°～110°时，升力系数呈缓慢下降趋势;在80°附近时升力系数约等于0;在110°时获得最小值－0.096;从110°～160°时又慢慢增大。扭转系数在20°时达到最大值0.586，在90°时达到最小值－0.752。

从图2(b)可以看出B模型的阻力系数和升力系数和图2(a)变化趋势基本一致，扭转系数区别较大，在0°和60°分别取得阻力系数的最小值0.488和最大值0.812，在20°和110°分别取得升力系数的最大值0.347和最小值 －0.157，在100°和70°分别获得扭转系数最小值－0.308和最大值0.091。

从图2(c)可以看出C模型的阻力系数、升力系数和扭转系数变化趋势与A模型基本一致，在0°和60°时分别获得阻力系数的最小值0.189和最大值0.807，在20°和110°时分别获得升力系数的最大值0.508和最小值－0.16，在130°和160°分别获得扭转系数的最小值－0.369和最大值0.161。

2.2 在10%紊流场中模型A、B、C的气动力均值

模型A、B、C在此风场的平均阻力系数、升力系数和扭矩系数分别如图3(a～c)所示。总体来说，3种模型的阻力系数和升力系数变化趋势与空风洞所得的结果一致，在扭转系数上面差异较大。

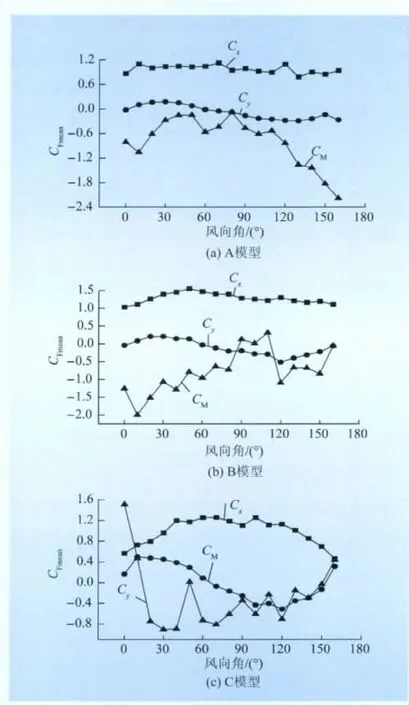
图3 在10%紊流场中模型力系数均值Fig.3 Average aerodynamic force coefficients of models in 10%turbulent flow field

从图3(a)可以看出，A模型在0°和80°分别取得阻力系数的最小值0.864和最大值1.126，在30°和130°取得升力系数的最大值 0.178和最小值－0.187，在80°和160°分别取得扭转系数的最大值－0.079和最小值－2.183。

从图3(b)可以看出，B模型在0°和50°分别取得阻力系数的最小值1.03和最大值1.554，在30°和120°分别取得升力系数的最大值0.208和最小值－0.51，在 10°和 110°分别获得扭转系数最小值－1.998和最大值0.313。

从图3(c)可以看出，C模型在0°和80°时分别获得阻力系数的最小值0.563和最大值1.259，在10°和120°时分别获得升力系数的最大值0.497和最小值－0.514，在0°和30°分别获得扭转系数的最大值1.51和最大值－0.904。

3 3种类型覆冰截面的驰振稳定性分析

3.1 驰振稳定性的判据

针对输电线路舞动现象有最经典的Den Hartog准则［2］和 Nigol准则［3-4］，在本文的分析中利用这 2个准则对不同风场条件下3种覆冰模型进行判定，是Den Hartog准则的必要条件，n=是Nigol准则的必要条件。用三次多项式来模拟升力系数、扭转系数随风攻角的变化，在均匀流场中m、n这2个系数如图4(a)、(b)所示。A、B、C这3种模型在所有实验工况的风向角下m都大于0，A、B、C这3种模型在70°风向角下取得各自的最小值0.54、0.34、0.14。在 Den Hartog准则下，3 种模型都没有可能发生驰振;A模型在20°～110°的风向角下n＜0，B 模型在50°～110°的风向角下 n＜0，C 模型在10°～90°的风向角下n＜0，模型有可能发生驰振。在10%紊流场中m、n这2个系数如图4(c)、(d)所示。

在Den Hartog准则下，A、B、C这3种模型在所有实验工况的风向角下m都大于0，不可能发生驰振;3种模型在80°风向角下取得各自的最小值0.58、0.86、0.35。A 模型在70°～160°风向角下 n＜0，B 模型在120°～160°风向角下 n＜0，C 模型在0°～60°和160°的风向角下n＜0，有可能发生驰振。

3.2 薄覆冰导线的驰振稳定性分析

从上面分析可以看出Den Hartog准则不适应薄覆冰的情况。Den Hartog准则是基于负阻尼理论，当导线处于某一个特定的风向角，导线向上振动时，由于覆冰导致截面不规则使导线具有向上的升力，这样就加剧了导线的运动使导线不稳定。同样，当导线向下振动时，不规则导线产生的向下的力也会加剧导线的运动而使导线运动不稳定［2］。和CL＞0这2个条件保证当导线向上运动时升力为正，所以在薄覆冰情况下，当满足和C＞0这2个L条件时，导线就会离开平衡位置而向上运动，进而有使导线驰振的可能性。

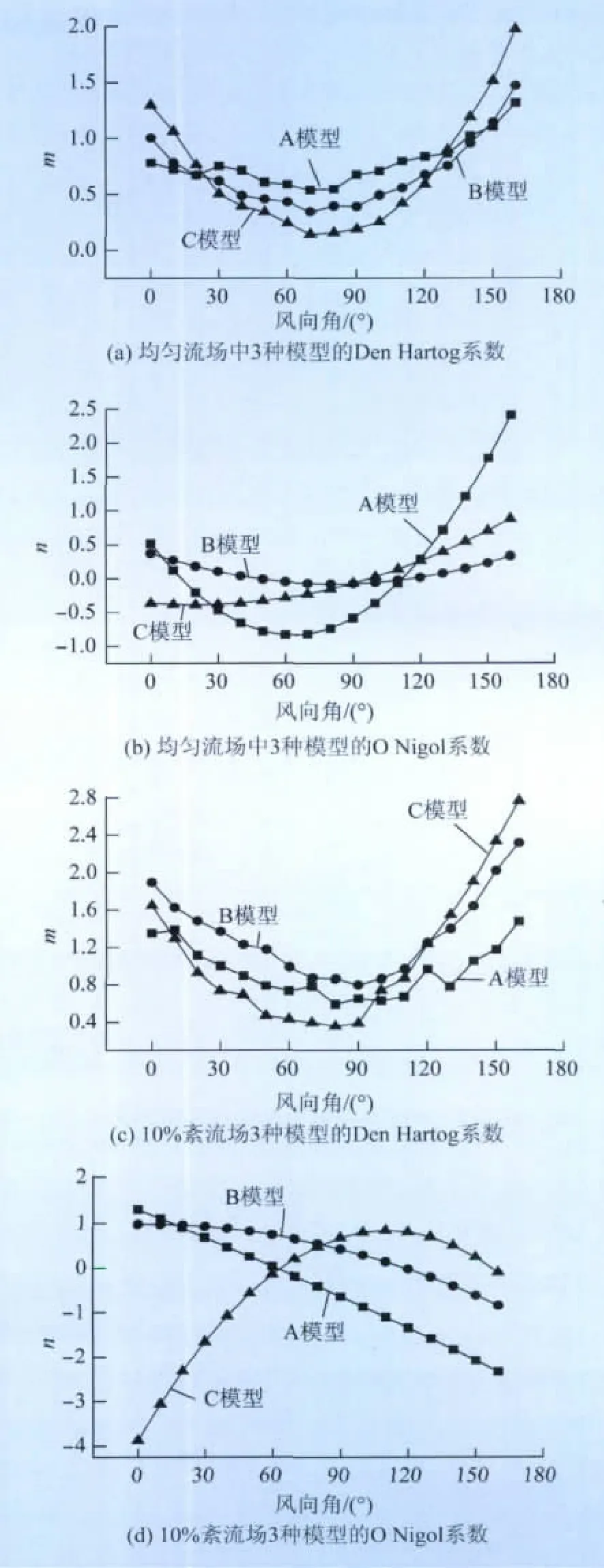
图4 3种模型的驰振不稳定性分析Fig.4 Galloping instability analysis of three models

从图5(a)结合升力系数图可以看出在均匀流场中A模型在20°～70°风向角、B 模型在30°～80°风向角、C模型在30°～80°风向角时可能发生驰振不稳定。从图5(b)结合升力系数图可以看出在10%紊流场中A模型在30°～50°风向角、B模型在30°～50°风向角、C模型在10°～60°风向角时可能发生驰振不稳定。而在实际情况下，覆冰大部分都发生在0°～90°风向角，这正好能够解释薄覆冰舞动这一现象。

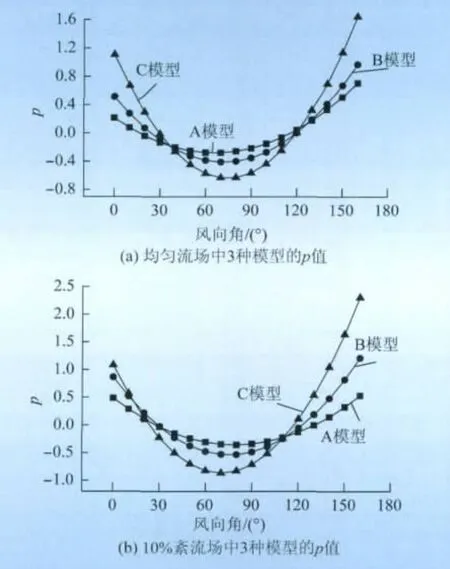
图5 3种模型的驰振不稳定性分析Fig.5 Galloping instability analysis of three models

4 结语

本文以薄覆冰导线为基础，在2种不同的风场条件下对典型覆冰导线(准椭圆形)模型进行了高频天平测力实验，获得了3种不同覆冰厚度导线在2种风场中的平均气动力系数，并利用DenHartog系数和Nigol系数对3种模型进行分析判断，验证了 Den Hartog判据不适合处理薄覆冰导线。根据Den Hartog准则的原理提出了针对薄覆冰导线的2个必要条件并进行分析，得到在均匀流场中A模型在20°～70°风向角、B 模型在 30°～80°风向角、C 模型在30°～80°风向角时可能发生驰振不稳定;在10%紊流场中A模型在30°～50°风向角、B模型在30°～50°风向角、C模型在10°～60°风向角时可能发生驰振不稳定。

致谢

感谢同济大学风工程系全涌、黄鹏老师在试验过程中给予的帮助和建议，感谢吴迪、张文杰等对本试验做出的贡献。

［1］湖南省电力试验研究院.12.27长沙、湘潭地区线路跳闸情况分析报告［R］.长沙:湖南省电力试验研究院，2009.

［2］郭应龙，李国兴，尤传永.输电线路舞动［M］.北京:中国电力出版社，2003.

［3］Den Hartog J P.Transmission Line vibration due to sleet［J］.Transactions AIEE，1932，51(4):1074-1086.

［4］Nigol O，Buchan P G.Conductor galloping-part 1:Denhartog mechanism［J］.IEEE Transactions on Power Apparatus and Systems，1981，PAS-100(2):699-707.

［5］Nigol O， Buchan P G.Conductorgalloping-part 2:Torsional mechanism［J］.IEEE Transactions on Power Apparatus and Systems，1981，PAS-100(2):708-720.

［6］Richardson A S.Predicting galloping amplitudes［J］.ASCE Journal of Engineering Mechanics，1988.114(4):716-723.

［7］RichardsonA S.Predicting galloping amplitudes:II［J］.Journal of Engineering Mechanics，1988，114(11):1945-1952.

［8］Yu P，Popplewell N，Shah A H.Instability trends of inertrially coupled galloping part I:Periodic vibrations［J］.Journal of Sound and Vibration.1995，183(4):663-678.

［9］Yu P，Desai Y M，Shah A H，et al.Three-degree-of-freedom model for galloping part I:Formulation［J］.ASCE Journal of Engineering Mechanics，1993，119(12):2404-2425.

［10］何锃，赵高煜.安装失谐摆的大跨越分裂导线自由振动计算［J］.中国电机工程学报，2003，23(2):63-66.

［11］何锃，赵高煜.分裂导线扭转舞动分析的动力学模型［J］.工程力学，2001，18(2):126-134.

［12］蒋兴良，张丽华.导线覆冰碰冻率及最大覆冰直径分析［J］.中国电机工程学报，1999，19(9):10-13.

［13］孙才新，蒋兴良，熊启新，等.导线覆冰及其干湿增长临界条件分析［J］.中国电机工程学报，2003，23(3):141-145.

［14］顾明，马文勇，全涌，等.两种典型覆冰导线气动力特性及稳定性分析［J］.同济大学学报:自然科学版，2009，37(10):1328-1332.

［15］顾明，马文勇，全涌，等.准椭圆形覆冰导线气动力特性实验研究［J］.同济大学学报:自然科学版，2010，38(10):1409-1413.

［16］GB 50009—2001建筑结构荷载规范［S］.北京:中国建筑工业出版社，2002.