基于超导储能装置的配电网谐波与电压凹陷补偿技术

谢奕尘，高二超，李瑞金

(安徽理工大学电气与信息工程学院，安徽省淮南市232001)

0 引言

当前配电网系统中广泛存在电压凹陷大、功率因数低和电网谐波比重大等问题。现有的无功发生器既可以进行无功补偿及滤波来提升电能质量，提高了配电网稳定性，还可以减少有功损耗和电压损失，同时降低了低电压配电系统中的线损［1-2］。但是当电力线路处于非正常运行或故障状态时，续流能力明显不足。

本文将设计一种超导储能装置(superconducting magnetic energy storage，SMES)，不仅能够解决当前无功发生器中存在的问题，还具有较高的续流能力［3］。非线性系统SMES装置可以实现多输入、多输出功能，其无功电流、有功电流和输出电压之间存在耦合关系。由于不解耦控制网络其稳定性不高，不能满足I型结构所要求的速动性，因此本文提出一种基于逆系统的直流电压前馈补偿和无功电流协调解耦控制策略，在此基础上应用内电流环控制器对已解耦的伪线性系统进行综合，实现 SMES的高性能解耦控制［4］。

1 SMES系统的基本原理

1.1 超导磁体的结构及基本原理

SMES是将电能储存在由持续电流产生的磁场中的一种装置，能高效、迅速地与系统交换有功功率和无功功率，其灵活的四象限运行能力可以有效地提高电力系统的稳定性。根据超导储能装置的结构特点和工作原理，充分发挥SMES的特点(既可以产生容性无功功率也可以产生感性无功功率)来减小其容量［5］。

迄今为止，用于电力系统的超导磁储能装置可分为 2 类［6］:(1)电流源型变流器(current source converter，CSC)SMES;(2)电压源型变流器(voltage source converter，VSC)SMES。由于VSC技术在可靠性和实用性方面比CSC好，因此本文选用了VSC。VSC型SMES的原理电路结构如图1所示。

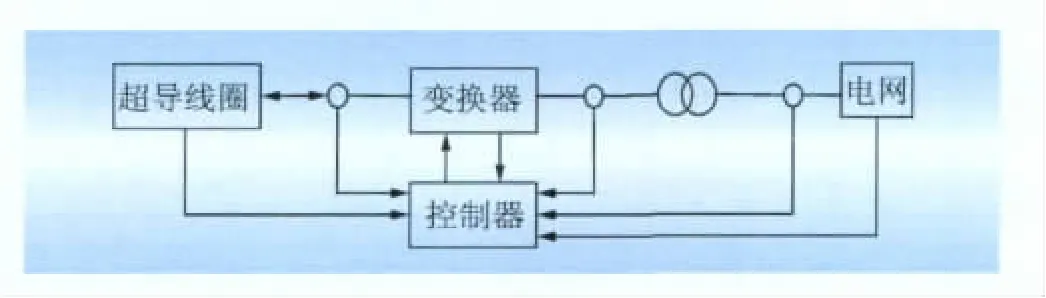
图1 SMES的原理结构Fig.1 Principle structure of SMES

图1中，SMES包含1个四象限电压源型变流器和1个二象限斩波器。由于二象限斩波器的主要功能是调节SMES电感电流，因此也称为电流调节器(current conditioning system，CCS)，出于稳压及滤波作用，两者间一般配有直流电容。电流调节器的开关管处于多种开关组合状态，本文使用六脉波脉宽调制(pulse width modulation，PWM)来调节直流电流和电容电压，对SMES吸收或发出的有功功率、无功功率进行调节。在VSC部分，通过调节直流侧电压和交流电压相角，就可以实现SMES与配电网间的有功和无功双向流动［7］。

超导线圈两端平均电压USMESav与电容器两端平均电压Udcav之间的关系为

式中j为占空比。当j=0.5时，超导线圈两端的电压为0，电流恒定，超导线圈与电网无能量流动。当j＜0.5时，电容两端电压上升，SMES释放电能。

1.2 系统的拓扑结构图

设电网电压恒定，可得有功功率和无功功率为

由式(2)可以看出，如果能实现对id，iq的独自解耦控制，就可以实现对有功功率、无功功率的控制。基于三相VSC的拓扑结构如图2所示。

图2 基于三相VSC的拓扑结构Fig.2 Topological structure based on three-phase VSC

在图2中，有功功率P、期望Q*为正值。无功功率Q由3部分组成:负载无功功率、滤波器的容性无功功率、SMES的无功功率Qs。本文由ΔQ=Q*－Q的感性或容性来对三相VSC进行调节，实现用容性无功功率把感性无功功率确定在特定范围内。

2 SMES模型的建立及控制系统设计

2.1 建立数学模型

三相VSC变流器的主电路如图3所示。

图3 三相VSC变流器主电路图Tab.3 Main circuit diagram of three-phase VSC converter

三相VSC变流器交流侧的滤波电容除了具有滤波作用，还起到确定负载电压凹陷的作用，根据基尔霍夫定理可得其状态方程为

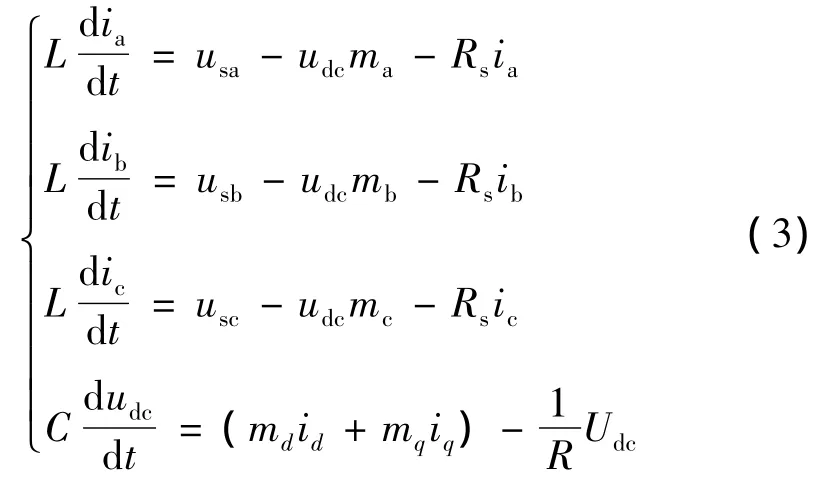
但是在三相静止坐标系下该控制策略无法实现，通过Clarke和Park变换，可得到在两相同步旋转dq坐标系下的方程为

设系统状态变量为

设系统输出变量为

设系统控制变量为

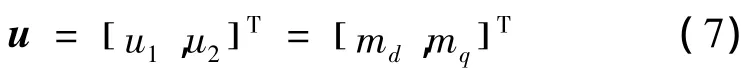
式中:id、iq分别为有功、无功电流分量;mk为开关函数;md、mq为dq坐标系下的开关函数;u1、u2为控制变量的变量因素。功率因数可调的三相VSC整流器系统输出量为直流电压Udc和无功电流分量iq。可将式(4)简化为

由式(8)可以看出，三相VSC是一个多输入、多输出的非线性系统。其无功电流、有功电流和输出电压之间存在着耦合关系，为了使无功电流和直流侧电压得到良好的控制效果就需要进行解耦。本文利用逆系统数学理论，求出三相VSC的逆系统，利用前馈补偿的方法，构建出解耦后的伪线性系统，然后利用线性控制理论的方法设计系统的控制策略。有

对SMES进行逆系统解耦控制，首先须求得SMES的a阶积分逆系统。利用逆系统求解方法对输出变量 y1，y2进行 α1，α2，α3，…，αr阶求导变换，直到出现输入控制量为止。式(9)作初等变换后得

此线性化矩阵变换后可知是非奇异矩阵，令原系统通过状态反馈化为α=[1，1]阶伪线性系统。并令对，对式(7)进行变换，可得SMES的逆系统为

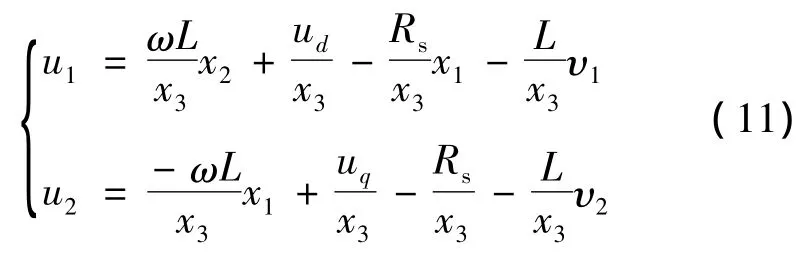
为了更直观地观察解耦的情形，可作如下线性变换

υ1，υ2为指令电流与反馈电流差的比例控制律，有

式中:Kq1和Kd1为控制系数。利用前馈补偿，可将式(13)和之前的伪线性系统连接在一起构成三相VSC变流器的闭环控制系统，实现了对电流分量iq和直流电压Udc的解耦。

2.2 建立电流环和CCS的控制方式以及VSC容量整定

根据VSC型SMES的工作模式，变换器及附件装置的控制策略分为电流环控制和电压环控制2个部分，由于电流环的作用更大，所以本文仅对电流环进行了设计。

(1)考虑到超导磁体不断充放电，为尽量减少对超导线圈的损害，采用带死区的比例积分(proportion integration，PI)调节器。这样可避免因微弱电压凹陷而动作变换。同时这种设置还可以防止较大的建模误差﹑提高了系统的快速反应和鲁棒性，内电流环PI调节器结构如图4所示。

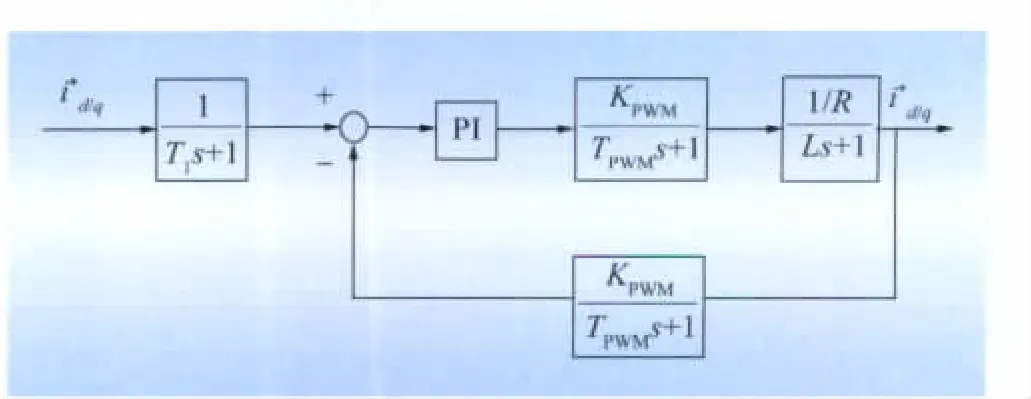
图4 内电流环PI调节器结构Tab.4 PI regulator structure of inner current loop

图4系统的开环传递函数为

系统的闭环传递函数为

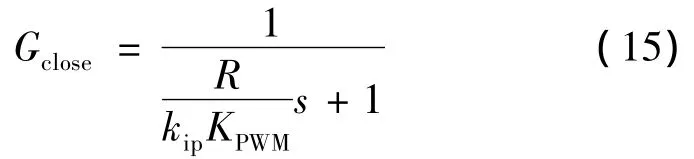
电流环PI调节器参数KiP，KiI分别为

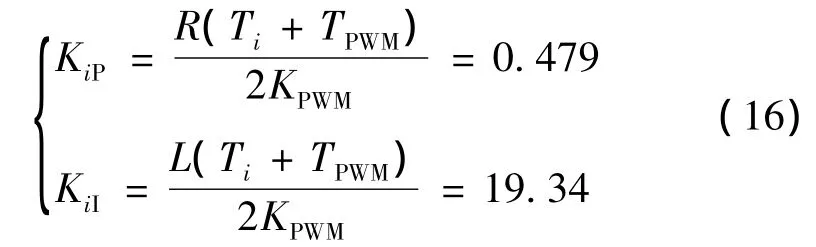
(2)电流调节环的控制设计。电流调节控制器的结构如图5所示。如果超导线圈的直流电流isc落在给定的范围内，且此时也有信号P*，则选择电压环工作，维持直流侧电压不变，确保整个系统处于正常的AC/DC切换状态。通过与三相VSC变流器的协调控制，实现了有功功率的双向流动。在其他情况下，都只有电流环工作，使超导电感的电流值能够达到电压源型SMES正常工作的要求。

图5 电流调节控制器的结构Tab.5 Structure of current regulation controller

(3)三相VSC的容量整定。本文引入等效电压和等效电流的概念，其值均为正序分量和负序分量平方和的平方根［6］。SMES的等效电压Ue和等效电流Ie分别为

当负载端开路时VSC的负序电流、正负序电压、负载的正负序电压、电网端的正负序电压之间存在如下关系:

式中:Us1，Us2，Zs为电网端的正、负序电压和电网端阻抗;Uc1，Uc2，Ic2为三相VSC端的正、负序电压和负序电流;UL2为非线性负载的负序电压。可得SMES的近似容量为

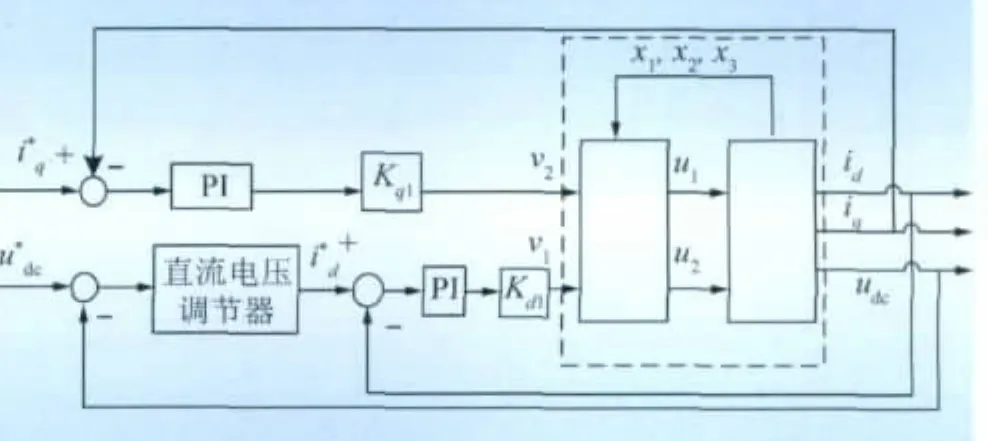
图6 SMES逆系统控制系统Fig.6 Control system of SMES inverse system

3 电能质量参数的仿真及分析

为了验证本文所述方法的有效性，用Matlab/Simulink对采用逆系统方法控制的三相VSC变流器进行了仿真。电网参数为Usm=311 V，f=50 Hz;交流侧参数为L=6 mH，Rs=0.5 Ω;直流侧参数为C=2 200 F，负载电阻为20 Q，直流侧给定电压=600 V，输出功率为18 kW。

3.1 电压凹陷补偿仿真

电压降落110 V时的电源电压波形如图7(a)所示，系统发生电压凹陷的起始时间为0.03 s，截止时间为0.09 s，过渡时间为0.06 s，系统电压凹陷期间电压降落了110 V，稳态幅值为300 V，凹陷期间电压幅值为190 V;电网电压突降为0的电源电压波形如图7(b)所示，如果电网电压在0.03 s发生供电中断，则瞬间电压从幅值300 V降至为0，在0.09 s供电恢复，供电中断时间为0.06 s。补偿后负载波电压波形如图8所示。由图8可以看出，补偿后的电网电压为298 V，稳态误差为0.7%。由于短时供电中断和电压暂降对电网系统的危害很大，持续时间为20 ms、深度为10%的电压突降就可能造成保护系统动作，通过补偿后的仿真波形可以看出，本文设计的PI控制器较为合理，能够得到较为理想的电网电压，而且在一定程度上消除了电网谐波的干扰，提高了系统的鲁棒性［8］。

3.2 无功补偿及谐波抑制仿真效果及分析

加入SMES装置后负载的P、Q波形如图9所示，由图9可见，采用SMES补偿无功后，无功功率的冲击现象得到有效抑制。无功功率曲线对于有功功率曲线具有良好的跟随性，只是幅值较小，仅为有功功幅值的0.48左右。鉴于配电网的实际运行能量及其输电线路的线损，功率因数基本稳定在设定的0.9，仅在非线性负载剧烈投切时功率因数才存在较小的跟随偏差。加入SMES装置后的匀速段谐波如图10所示，由图10可知，加入SMES装置后的匀速段谐波图基波含量较高，谐波含量很小几乎可以忽略不计，所以在加入SMES装置补偿后对电网谐波的抑制效果非常明显，有效地减少了谐波含量。如果没有三相VSC变流器以及FC的加入，则SMES瞬时补偿的无功功率较大，且波动剧烈，对整个系统将产生不利的影响。

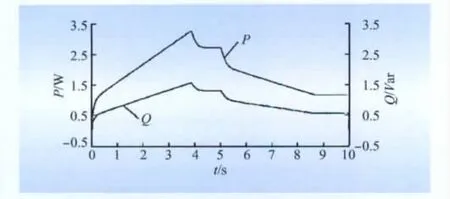
图9 加入SMES装置后负载的P、Q波形Fig.9 P，Q waveform of load after using SMES

图10 加入SMES装置后的匀速段谐波Fig.10 Harmonic with constant velocity after using SMES

4 结论

(1)利用SMES可以补偿电网电压的不平衡，也可以补偿由负载不平衡引起的电压凹陷。

(2)在补偿电网电压不平衡时，SMES除吸收维持直流侧电容、电压稳定的少量有功能量外，与电网之间只交换无功功率。

(3)在建立三相VSC的非线性数学模型基础上，提出了SMES的逆系统内电流环控制策略。

［1］黄妤群.SVG无功补偿技术在低压配电网中的应用［J］.电气工程与自动化，2011(12):44-45.

［2］庄淑瑾，孙玉坤，任明炜，等.静止无功发生器的预测电流控制方法SVG控制系统的稳定性研究［J］.电力自动化设备，2008，28(11):53-55.

［3］Michael J N，Donaid G H，John G N.A dynamic voltage restorer with selective harmonic compensation at medium voltage level［C］//38TH IAS Annual Meeting Conference，2003(2):1228-1235.

［4］Chang Jiangzhan，Vigna K，Ramaehand A，et al.Dynamic voltage restorer based Oil VSC PWM［J］.IEEE Transactions on Industry Applications，2001，37(6):855-1863.

［5］CHOIS S S，Li B H，Vilathgamuwa D M.Design and analysis of the inverter-side filter used in the dynamic voltage restorer［J］.IEEE Transactions Oil Power Delivry，2002，17(3):857-864.

［6］张辉，路亚新，钟彦儒.一种改善电力系统性能的SMES解耦控制策略及其仿真研究［J］.西安交通大学学报，2008，24(1):22-24.

［7］龚锦霞，卢婧婧，解大，等.一种新型动态无功补偿器的控制算法［J］.电力自动化设备，2009，29(5):89-93.

［8］刘水强，张颖，陈继业.基于同步坐标的有源电力滤波器检测策略［J］.电力自动化设备，2009，29(11):41-44.