基于虚长度法的高速双体船兴波阻力预报

李志恒，陈庆任，祝海勇，郑立捷

1 中国舰船研究设计中心，湖北武汉430064

2 中国船级社武汉规范研究所，湖北武汉430022

0 引 言

随着计算机容量的快速发展和高速船舶市场的不断扩大，高速双体船的阻力计算研究逐渐活跃。在高速双体船的阻力成分中，由于兴波阻力占的比重较大，且在兴波阻力研究方面已做过大量实验，有一定的实验数据基础，其理论研究结果易与实验结果比较，因而有关高速双体船的兴波阻力研究也十分活跃。

Couser 等［1-2］对带有方尾的高速双体船开展了大量理论研究，同时完成了NPL 系列船型的兴波阻力实验工作。Tarafder 和Suzuki［3］基于势流的边界元法，对双体船的非线性兴波问题进行了研究，考虑了两片体之间的侧向力。尹巍和高高［4］基于非均匀有理B 样条的广义高阶面元法，采用数值方尾边界条件对高速多体船兴波阻力进行了计算。王中等［5］利用改进的Michell 线性薄船兴波阻力理论，结合柯钦函数的精确积分解析表达式，对多体船兴波阻力进行了数值计算。刘军和易宏［6］应用Michell 薄船理论，利用“帐篷函数”对船体表面及流场进行了线性近似，建立了数值计算模型，并对SWATH 兴波阻力予以了计算。段晔鑫等［7］基于片体柯钦函数，对多体船兴波阻力予以了求解，得出了多体船的线性兴波阻力公式，并结合CFD 软件进一步分析了五体船的阻力及片体兴波干扰特性。

方尾的绕流问题比较复杂，对方尾的处理有一定的技术难度。本文将应用经典薄船理论［8］，以Michell 兴波阻力积分公式为基础，针对高速船的方尾船型特点，采用“虚长度”法，即在方尾后增加一个虚拟附体以使尾部封闭，通过对文献［2］中NPL 船模系列（包括3b，4a，4b，4c，5a，5b，5c，6a，6b，6c 共10 条船型）的数据进行分析，总结得到一个计算虚长度的公式，同时，对代号分别为4a，5c，6b 的3 种船型的兴波阻力进行数值计算并与Mol⁃land 等得出的实验数据进行比较。

1 理论基础

取固定在船体上的笛卡尔坐标系o-xyz，原点位于双体船中央，oxy 平面位于静水面上，x 轴沿均匀来流指向船尾，z轴垂直向上。

由薄船理论及Michell 兴波阻力积分公式［9］，可推导出双体船兴波阻力计算公式

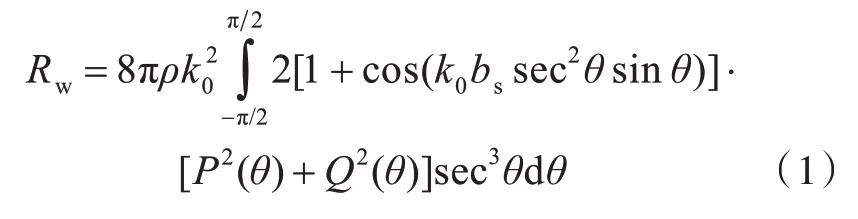
其中

式中：P(θ)和Q(θ)分别为余弦波波幅函数和正弦波波幅函数；θ 为波向角；S0为船舯剖面面积；U为船速；k0为波数；bs为双体船片体间距；∂f(x，z)/∂x 为船体型线的纵向梯度。

由Rw表达式可知，双体船兴波阻力由两部分组成：第1 部分是两片体分别产生的兴波阻力的叠加；第2 部分是由二者之间的相互干扰引起的阻力。

兴波系数Cw可以写成

式中，S 为船体湿表面面积。

在傅汝德数Fn＞0.45 的高速情况下，方尾船型船尾部的水流具有足够的动能，可以克服粘性的影响而迅速脱离开船尾部，从而在船后形成鸡尾状的水丘。水丘与尾板之间会形成一个“空穴”，空穴的长度∇L 即称为“虚长度”。实验观察与测量表明，其大小与船体主参数以及航速有关［10］。

通过对文献［1］中NPL 船型系列的计算进行总结分析，本文得出了“虚长度”的计算公式

式中：btrans为方尾处剖面的宽度；系数k 是一个关于船长宽比、宽度吃水比及傅汝德数Fn 的函数，其表达式为

2 程序介绍

计算程序采用了多个子函数嵌套调用的结构，其中包括样条插值函数、中剖面网格划分，以及其单元参数计算、点源源强计算、兴波阻力积分计算及结果后处理等多个子函数。其计算过程如下：

1）输入船舶主参数和横剖面型值，由样条插值函数模块生成中剖面型值；

2）由输入的初始速度确定初始傅汝德数，再由公式（3）和公式（4）计算出虚长度，然后，利用样条插值函数模块沿方尾处型线顺延生成假尾轮廓，进而得到假尾中剖面型值；

3）调用网格划分模块生成中剖面计算网格，并计算各网格单元的形心和面积等参数；

4）在单元形心处布源，通过样条插值函数模块得到半宽水线型值，然后再求出点源源强；

5）利用兴波阻力积分模块进行兴波阻力计算；

6）增大傅汝德数，进行下一循环的计算，直至Fn=1.1；

7）输出从输入的起始傅汝德数至Fn=1.1 之间总的兴波阻力计算数据。

计算程序的结构框图如图1 所示，整个计算程序用C 语言编制。

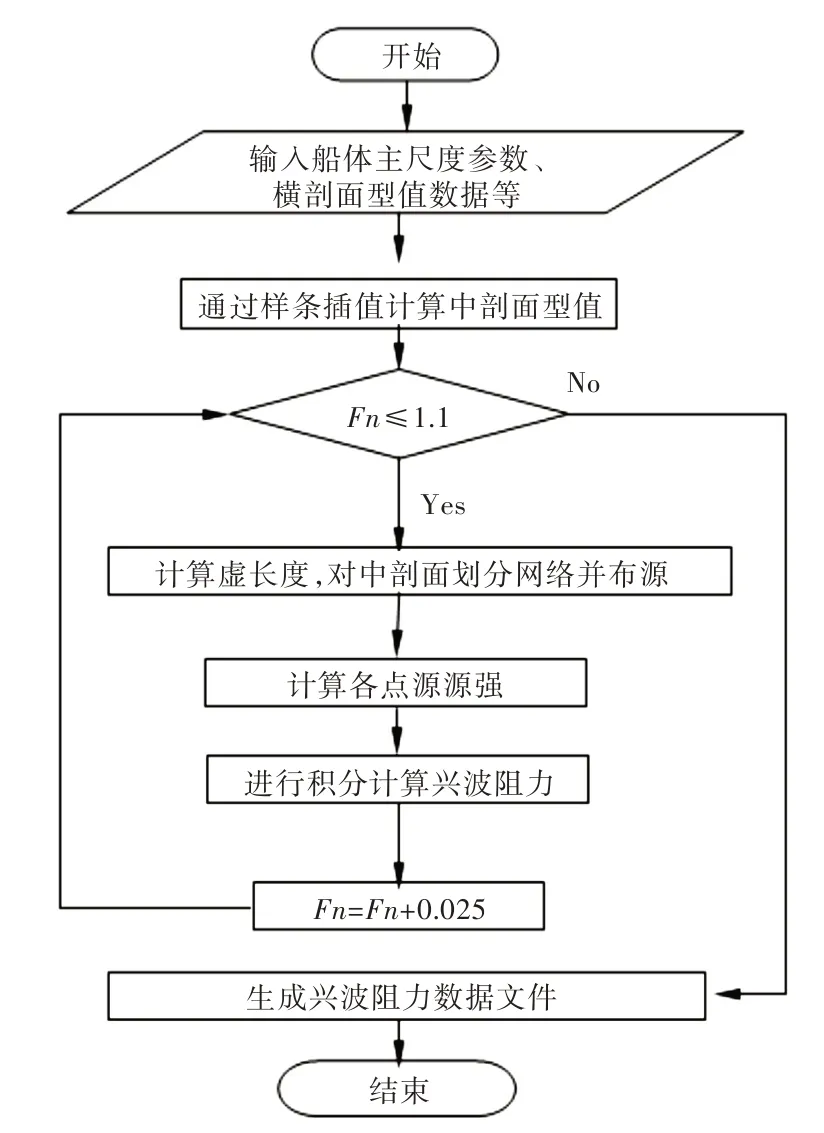
图1 计算流程图Fig.1 Calculation flow chart

3 结果讨论与分析

本文对NPL 船型系列中代号分别为4a，5c，6b的单体模型构成的双体模型船进行了计算，其船型参数如表1 所示。3 艘模型船的L/B 和B/T 都不同，故有利于进行结果分析。

文献［2］对由实验测得的波形数据进行分析计算，得到了兴波阻力Cw。本文将船模两片体间距bs/L 分别为0.2，0.3，0.4 和0.5 这4 种情况进行了分析计算，并在bs/L 的值不同的情况下与文献［2］的实验数据进行了对比。

3.1 船模4a 的计算结果

将船模4a 在不同片体间距比条件下的兴波阻力计算结果与文献［2］的实验数据进行了比较，如图2 所示。由图中可看出，bs/L= 0.2，0.3，0.4，0.5 的计算结果在趋势上与实验数据取得了很好的一致性，只是在低傅汝德数阶段（Fn ＜0.3）误差较大，而在剔除个别异常实验数据点后，高傅汝德数下的误差均在5%以内。

表1 模型船的基本参数Tab.1 The basic parameters of the model boat

图2 船模4a 的计算结果与实验数据对比Fig.2 The comparison of calculation results and experimental data of 4a

3.2 船模5c 的计算结果

将船模5c 在不同片体间距比条件下的兴波阻力计算结果与文献［2］的实验数据进行了比较，其结果如图3 所示。

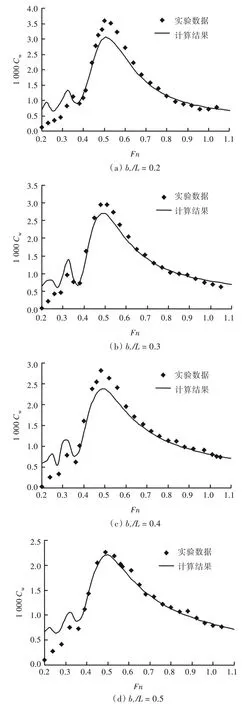
图3 船模5c 的计算结果与实验数据对比Fig.3 The comparison of calculation results and experimental data of 5c

由图中可看出，由于计算精度的原因，在Fn=0.5 附近处，计算结果的曲线峰值存在明显误差，而在Fn ＞0.6 时则与实验数据吻合较好，误差在6%以内，其中bs/L = 0.5 时的结果与实验数据很逼近。通过船模两片体间距bs/L = 0.2，0.3，0.4，0.5 这4 种不同值情况下的比较不难看出，bs/L 值越大，兴波阻力系数越小。

3.3 船模6b 的计算结果

将船模6b 在不同片体间距比条件下的兴波阻力计算结果与文献［2］的实验数据进行了比较，如图4 所示。从中可以看出，当Fn ＞0.4 时，计算结果与实验数据吻合较好，其中bs/L=0.2，0.3 时的曲线峰值存在一定的误差，而在排除个别由实验精度造成的异常实验数据点（实验测得波形后，是通过公式计算得到兴波阻力，因此实验结果与实际结果会有一定的误差，由此产生个别异常点）后，计算误差在6%以内。

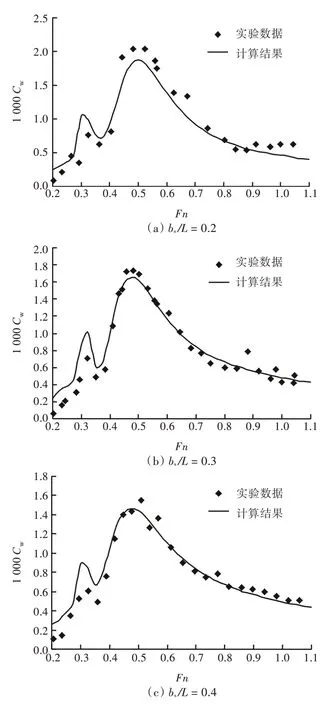
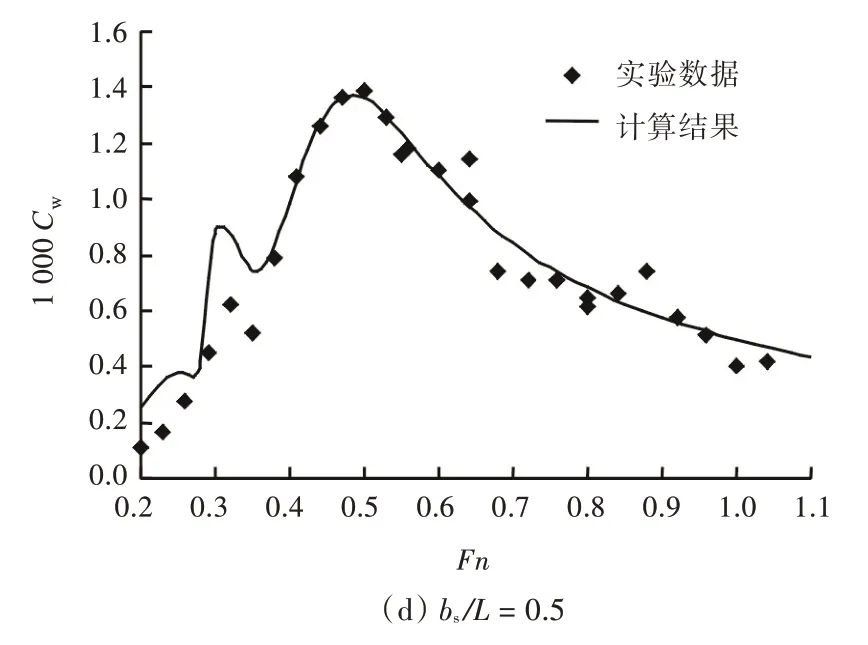
图4 船模6b 的计算结果与实验数据对比Fig.4 The comparison of calculation results and experimental data of 6b

4 结 论

本文应用经典薄船理论，以Michell 兴波阻力积分公式为基础，采用“虚长度”法，对NPL 系列船型中的3 条双体船（Fn = 0.2～1.1）进行了兴波阻力计算，并与文献中的实验数据进行了比较，得出以下结论：

1）利用“虚长度”法进行双体船兴波阻力预报时，虚长度大小的确定是一个关键。本文通过对文献结果的分析总结，以及基于理论的计算验证，得出了一个虚长度计算式，计算结果证明，所给出的“虚长度”计算公式是有效的。

2）本文采用“虚长度”法计算了文献［2］中3种双体船的兴波阻力，并将计算结果与实验数据进行了比较，两者在趋势上取得了较好的一致性。其中，在低傅汝德数阶段（Fn ＜0.3）误差较大，而在高傅汝德数阶段（Fn ＞0.6），误差则均在6%以内，这表明此方法在高速情况下具有较高的计算精度，适于工程上对方尾双体船兴波阻力的快速预报。

3）基于本文方法编制的计算程序操作方便，快捷有效，能够为船舶方案论证及船型优化设计提供支持。

［1］COUSER P R，WELLICOME J F，MOLLAND A F.An improved method for the theoretical prediction of the wave resistance of transom-stern hulls using a slen⁃der body approach［J］. International Shipbuilding Prog⁃ress，1998，45（444）：331-349.

［2］MOLLAND A F，WELLICOME J F，COUSER P R.Resistance experiments on a systematic series of high speed displacement catamaran forms： variation of length-displacement ratio and breadth-draught radio［J］. Transactions of The Royal Institution of Naval Ar⁃chitects，1994，71：55-71.

［3］TARAFDER M S，SUZUKI K. Computation of wave making resistance of a catamaran in deep water using a potential-based panel method［J］. Ocean Engineering，2007，34（13）：1892-1900.

［4］尹巍，高高.方尾边界条件在高速多体船兴波阻力计算中的应用［J］.船海工程，2008，37（5）：6-9.YIN Wei，GAO Gao. Application of transom-stern boundary conditions in numerical computation for the Wave-making resistance of high-speed multi-hull ships［J］. Ship and Ocean Engineering，2008，37（5）：6-9.

［5］王中，卢晓平，钟士岗. 单元柯钦函数精确积分的多体船兴波阻力计算［J］.哈尔滨工程大学学报，2009，30（6）：602-606.WANG Zhong，LU Xiaoping，ZHONG Shigang. Calcu⁃lating the wave making resistance of multi-hull ships based on an integral expression of the Kochin function on the surface panels［J］. Journal of Harbin Engineer⁃ing University，2009，30（6）：602-606.

［6］刘军，易宏.小水线面双体船兴波阻力特性研究［J］.武汉理工大学学报（交通科学与工程版），2010，34（1）：117-121.LIU Jun，YI Hong. A research about wave-making re⁃sistance characteristic of small water plane area twin hull［J］. Journal of Wuhan University of Technology（Transportation Science and Engineering），2010，34（1）：117-121.

［7］段晔鑫，卢晓平，王毅，等.五体船兴波阻力线性理论计算与CFD 数值模拟［J］. 中国舰船研究，2011，6（6）：1-7，22.DUAN Yexin，LU Xiaoping，WANG Yi，et al. Calcula⁃tion of wave resistance by linear theory and CFD simu⁃lation for pentamaran［J］. Chinese Journal of Ship Re⁃search，2011，6（6）：1-7，22.

［8］刘应中. 船舶兴波阻力理论［M］. 北京：国防工业出版社，2003.

［9］ROBARD S W.The hydrodynamics of high-speed tran⁃som-stern vessels［D］.New South Wales：The Universi⁃ty of New South Wales，2008.

［10］TARAFDER M S，KHALIL G M，SAHA G K. Analy⁃sis of transom stern flows by modified Rankine source panel method［C］//Proceedings of the 8th Internation⁃al Conference on Mechanical Engineering. Dhaka，Bangladesh，2009：1-5.