多块结构化网格在高速水面舰船阻力计算中的应用

周 芃，李 为，陈韬颖

中国舰船研究设计中心，上海201108

0 引 言

随着计算机性能的逐渐提高，用计算流体动力学（CFD）软件模拟船体粘性兴波流场已成为可能。与试验验证相比，CFD 数值模拟技术具有信息量大、成本低、易并行化及能快速响应等特点，但其预报精度一直是船舶CFD 研究者及船舶设计人员高度关注的问题。

船舶在静水中航行时，其表面压力分布会随之改变，导致船体表面受力不平衡，故而导致航态变化。表面压力主要是船舶在航行中受到的流体对其表面动压力及粘性力的影响，表面压力会导致垂向力和纵倾力矩发生变化，从而引起升沉与纵倾［1］。可见船舶实际航行的姿态与理论计算时的设计吃水正浮状态是有区别的，尤其是对于高速舰船，其升沉和纵倾与低速状态相比更为明显。因此，在进行理论计算时就应该考虑航态的变化。由于船舶形状左右对称，因此，只考虑在纵向上的升沉及垂向上的纵倾。

目前，在计及航态影响的船舶阻力预报研究方面，国内外学者已进行了一些研究。在国外，Dawson［2］早 在1979年就采用Rankine 面元法，并考虑升沉和纵倾的影响研究了兴波问题，但这些方法都是建立在弱非线性基础上，依靠设计浮态下的船舶水动力系数对姿态进行预报，而非基于船体水动力平衡状态下的计算；Yang 等［3］采用非结构化网格和有限元法，对S60 船型计及升沉与纵倾的兴波流场进行了计算，但未考虑流体粘性的影响，计算结果与试验结果尚有一定的差距。在国内，张志荣等［4］对水面舰船绕流场进行了数值模拟，并将阻力计算结果和兴波波形与试验结果进行对比，验证了CFD 在水面舰船阻力方面的可行性；曹洪建［5］对航态变化更大的滑行艇绕流场进行了数值模拟，其航态变化是通过试验获得，而非数值计算得到。近年来，部分学者将船舶航态作为求解的一部分对水面舰船的绕流场进行数值计算。董文才等［6］对中高速深V 船型进行了计及升沉和纵倾的船舶阻力预报，其方法是首先计算正浮状态的船体升力与纵摇力矩，根据该升力和纵摇力矩与静浮力和纵倾矩的平衡来调整船舶航态，然后根据调整后的航态再次建模并进行数值计算，如此重复多次得到稳定、平衡的船舶航态，进而得到船舶的阻力，其计算阻力值与试验值的误差均在5%以内。倪崇本等［7］采用动网格技术对高速多体船进行了计及航态的阻力预报，该方法无需多次建模和重复求解，计算更加简便。

动网格的一个关键技术是边界运动更新时，网格也随之更新，并且不能出现负体积网格。但由于船舶表面形状较复杂，目前的动网格技术还不能满足计算要求。本文的研究是基于静态平衡法，但在该方法的基础上作出假设进行了改进，无需多次建模，只需进行迭代计算即可，大大降低了工作量。通过数值计算，得到了傅氏数在0.176～0.441 范围内的船模阻力，并在傅氏数大于0.35 时计及了航态迭代计算，其与船模试验值的误差均在5%以内。另外，通过分析不同傅氏数下的自由表面波形图和波形等值线图，分析了其艏艉兴波随航速的变化情况，符合试验验证结果。

1 流场数值模拟

1.1 控制方程与湍流模型

船舶绕流场属高度复杂的三维流动，其主要原因是船首尾形状复杂、曲率变化大等，这一复杂的特性主要体现在船的艉部伴流中。在数值计算的准确程度方面，湍流模型的选取会直接影响其精度［8-9］。本文将采用商业软件CFX 中RNG k-ε湍流模型进行模拟，湍流模型及控制方程［10］如下。

在直角坐标系下，不可压缩牛顿流体连续性方程与RANS 方程为

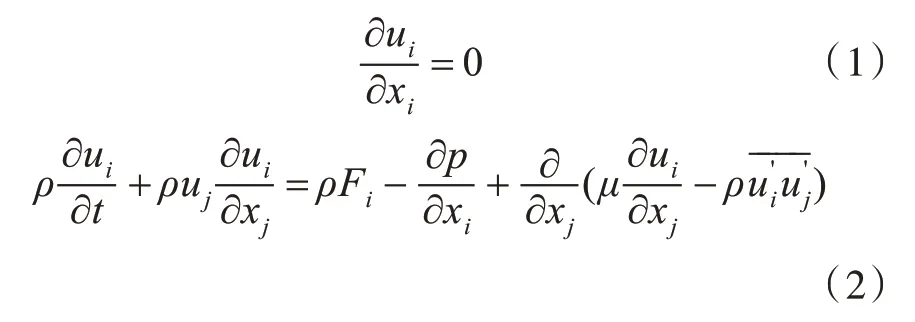
式中：ρ 为密度；μ 为流体粘性系数；p 为平均压力；Fi为外力项；ui为时均速度；u'i 为脉动速度；与脉动速度相关的项称为雷诺应力。

文中采用的湍流模型是RNG k-ε模型，这种模型是标准k-ε模型的改进形式，它修正了湍动粘度，考虑了平均流动中的旋转及旋流流动情况，增加了反映主流的时均应变率。该模型是一种适合船舶流场计算的湍流模型，其方程形式如下。

湍流动能方程与耗散率方程［11］：

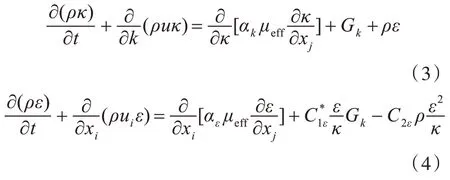
1.2 浮态调整方程

将船舶看成是一个刚体，其在静水航行稳定时，必须满足力和力矩平衡。

式中：F 为外力；M 为外力对重心处的力矩。以上式（5）和式（6）称为浮态平衡方程。

本文采取的是一种简化形式的迭代计算。首先，假设船舶在升沉时水线面面积保持设计水线面面积不变；其次，浮态调整运动十分缓慢。

基于以上两点假设，升沉和纵倾的公式可由以下等式给出：

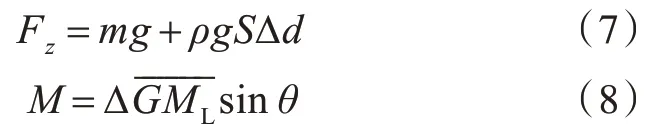
式中：Fz为船体所受压力在z 方向（垂向）的分量；m 为船体的质量；Δd 为船体的升沉值（下沉为正）；S 为设计水线面面积；M 为压力对船体重心处的力矩在y 方向（横向）的分量；Δ 为船体排水量；为船体的纵稳性高；θ 为船体纵倾角（以艉倾为正）。根据计算算出的垂向力和力矩验证平衡方程，如果不满足平衡方程（5）和方程（6），便带入式（7）和式（8），算出浮态调整量，改变船舶的浮态，重新进行计算。

1.3 计算模型与网格划分

1.3.1 计算模型

本文以某高速舰船为研究对象，CFD 计算采用1∶19.756 8 的缩小模型，模型建立至设计水线上的一定高度处。模型主要参数如表1 所示。

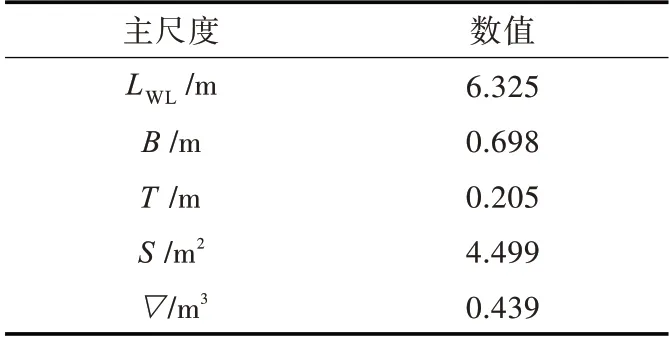
表1 船模主要参数Tab.1 Principle parameters of ship model

模型的建立在三维建模软件UG NX7.5 中进行。将各横剖线、水线联合形成船艏、船舯和船艉曲面，其三维模型如图1 所示。

图1 三维模型Fig.1 The 3D model of computation object

1.3.2 计算域及边界条件

由于计算模型是沿中纵剖面完全对称，故为便于计算，仅取一半模型进行几何建模和网格划分，另一半做镜像处理。为了使计算结果尽量不受边界条件的影响，将外流域场设为长方体，具体设置如下：

1）水域：将船艏向上游延伸至1 倍船长处设为水域速度入口；船艉向下游延伸至3 倍船长处设为水域压力出口；距中纵剖面5 倍半宽值处为水域外边界，设为开放式边界；设计水线面向下延伸5 倍半宽处为水域底部，设为滑移壁面。其速度大小为来流速度，方向指向船艉。

2）空气域：在设计水线面上增加一个深度为舰船吃水高度1.5 倍的空气层。边界条件与水域完全类似。

3）船表面：设为不可滑移壁面边界。

1.3.3 网格划分

计算网格的质量会直接影响到计算的可行性、收敛性以及其计算精度。本文采用的是计算精度更高、收敛性更好的全船结构化网格，总数约156 万。计算网格在ICEM 中生成，采用O-H 多块结构化网格，即纵向为H 型网格，横向为O 型网格。为了更精确地计算摩擦阻力，在船体表面向外生成一层O-grid 划分边界层网格，使y+控制在30 左右。在网格划分过程中，保证靠近船体表面的网格密，远离船体表面的逐渐变疏；在船体表面，保证艏、艉部的网格与中部和顶部相比更密。这样，就能保证在控制网格数量的同时达到理想的计算精度。图2 所示为计算域网格划分情况，图3～图5 所示为局部网格划分情况。

图2 计算域网格Fig.2 Grid system of computational region

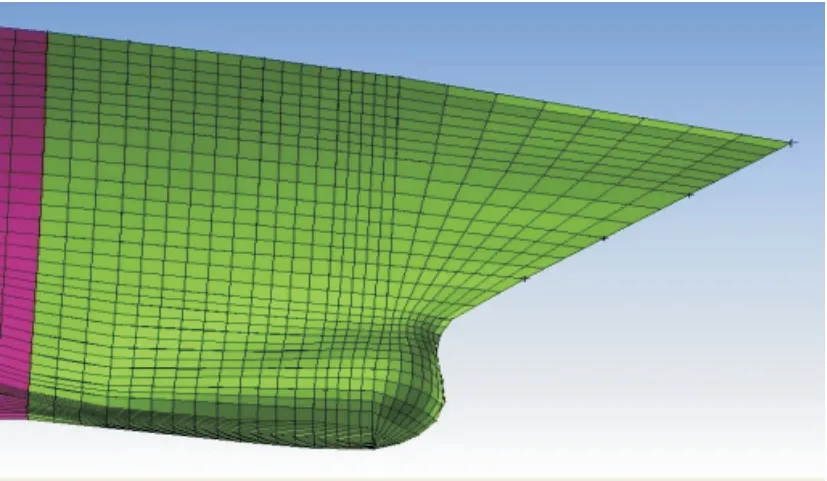
图3 艏部网格Fig.3 The grid of foreship

图4 艉部网格Fig.4 The grid of stern

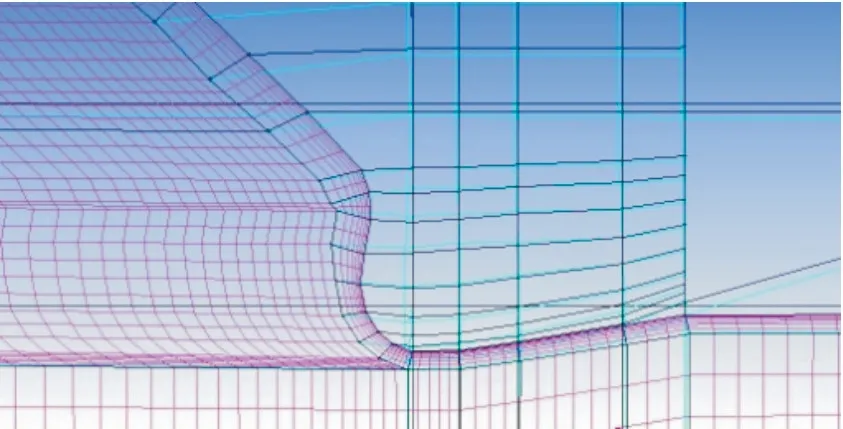
图5 船艏的对称面及边界层网格Fig.5 The boundary grid of symmetry at foreship

1.4 计算结果及分析

1.4.1 阻力计算结果及分析

1）不考虑航态变化。

按照上述网格划分方法及边界条件设置，将网格导入计算流体动力学软件CFX 中进行气、液两相流数值计算，湍流模型采用RNG k-ε模型。船模试验结果与数值结果按照二因次法进行阻力换算，采用柏—许公式计算相当平板的摩擦阻力系数（Cf=0.455/（logRe）2.58，其中Re 为雷诺数）。

取ρ = 998 kg/m3，ρ海水= 1 025.91 kg/m3，ν =0.892 92×10-6m-2·s-1，ν海水= 1.188 31×10-6m-2·s-1，计算得到的试验值各速度下的阻力如表2 所示。

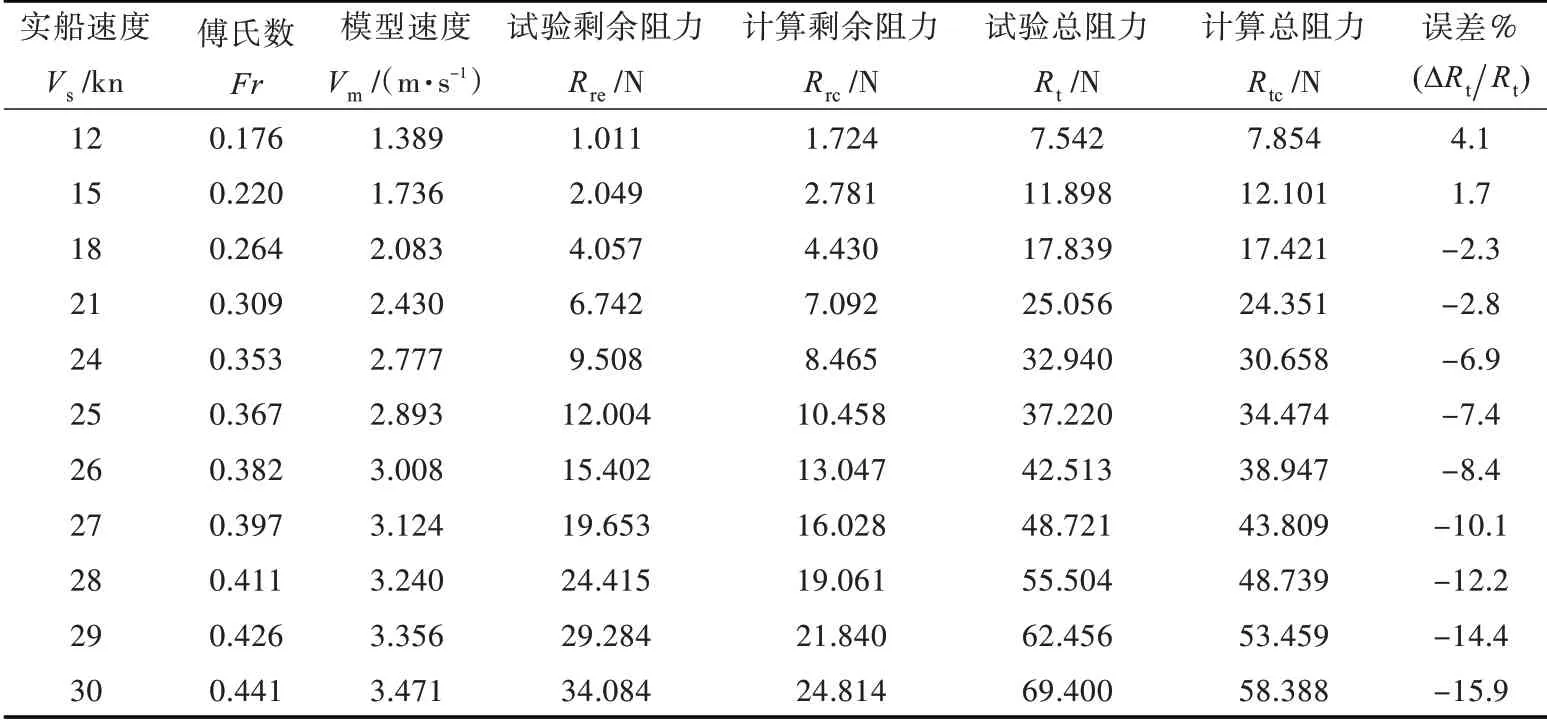
表2 不考虑航态下阻力计算值与试验值的比较Tab.2 The comparison of resistances from computation results and experiment data in fix pose

根据上述计算结果可知，对于高速舰船的阻力，在傅氏数低于0.35 左右时，由于航态变化较小，对阻力计算影响的误差不大，因此误差在可接受范围内。但随着航速的增加，计算得出的阻力误差在傅氏数大于0.4 时甚至会超过10%。这是因为随着航速的增加，船体的升沉和纵倾变化越来越明显，而计算时默认的设计吃水正浮状态与实际的航行姿态差距较大，从而导致船体兴波和船体表面的压力分布与真实状态不相符合，因此计算达不到工程应用的精度。

2）在傅氏数大于0.35 时考虑航态变化。

根据正浮状态各速度下的理论计算结果，可分别求解船体表面力和力矩的积分，并将其带入力和力矩平衡方程进行验证，若不满足，便将其带入式（7）、式（8）进行升沉和纵倾值的调节，然后再改变航态重新进行计算。

表3 所示为浮态调整计算的基本参数。以基线与中横剖面的交点为原点，坐标系定义如下：x轴为中纵剖面与基平面的交线，以指向船首为正；y 轴为中横剖面与基平面的交线方向，以指向右舷为正；z 轴按右手法则确定。

表3 浮态调整计算基本参数Tab.3 Basic parameters of pose adjustment

静态平衡法的人工实现：根据正浮状态下的理论计算结果，分别求解船体表面压力沿z 方向（垂向力）的分量，以及压力在重心处的力矩沿y轴的分量。计算得到调整的升沉值和纵倾值后，在ICEM 中进行模型与块的平移和旋转，重新进行计算。此方法无需重新建模和网格划分，大大减少了工作量。由此，便可得到新的垂向力及压力在重心处的力矩沿y 轴的分量。重新调整航态计算，直至垂向力与重力之差小于重力的3%，便可认为压力与重力平衡了，无需继续调整。一般经过1～2 次迭代即可达到平衡。调整航态后的阻力计算结果与试验值的对比如表4 和图6、图7所示。

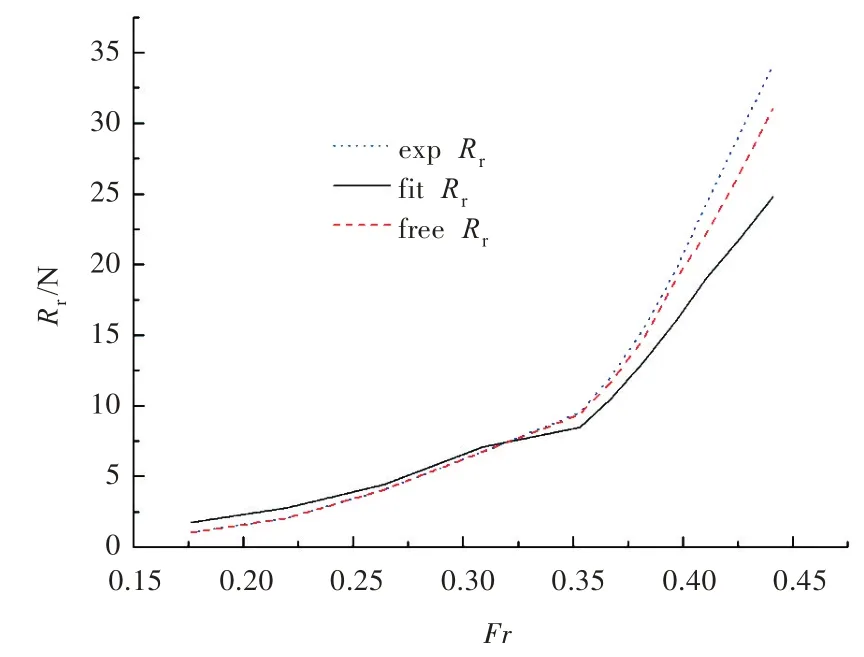
图6 航态变化前后与试验值剩余阻力比较Fig.6 The comparison of residual resistances

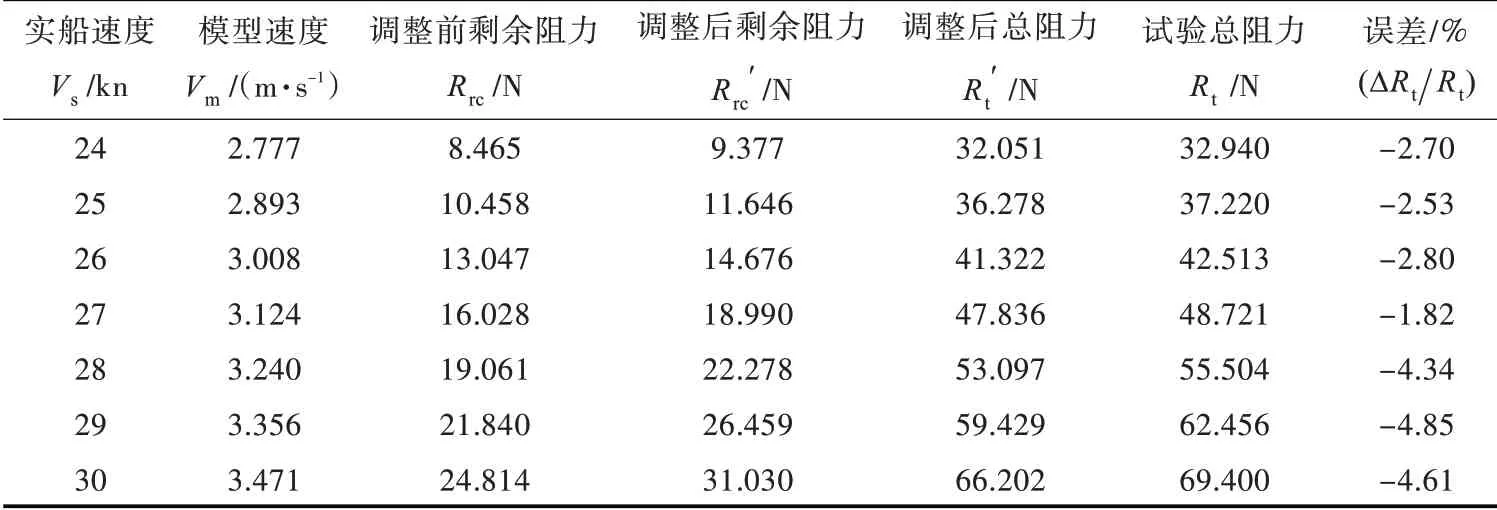
表4 航态调整后阻力计算值与试验值比较Tab.4 The comparison of resistances from computation results and experiment data in free pose

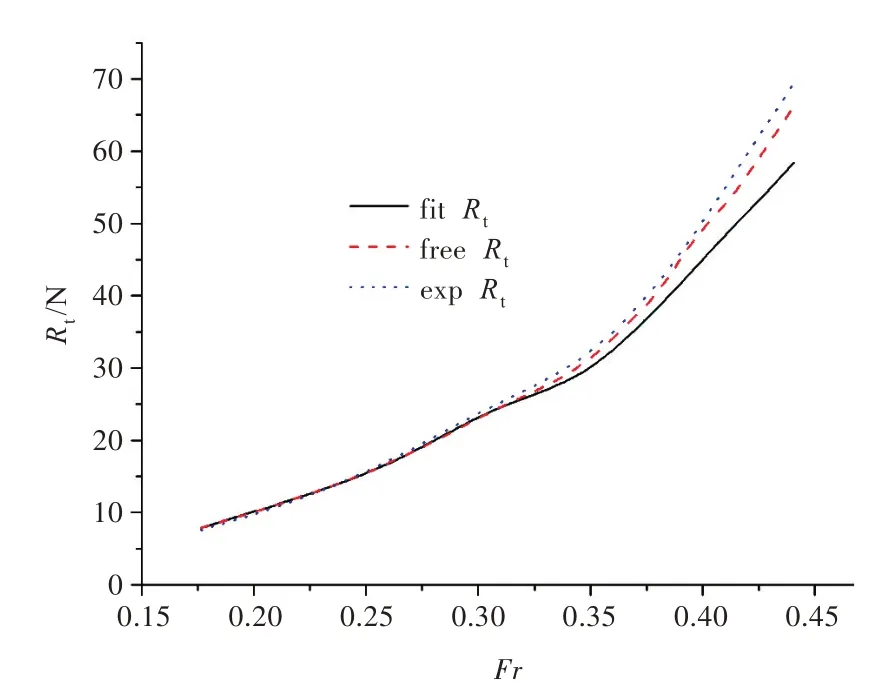
图7 航态变化前后与试验值总阻力比较Fig.7 The comparison of total resistances

从表4、图6 和图7 可以看出，计及升沉和纵倾后，计算值与试验值的误差均在5%以内，吻合度较好。同时也可以看出，航态的变化使摩擦阻力更接近试验换算值，其变化对摩擦阻力影响较小，而对兴波阻力影响则较大；低速时航态的变化对总阻力影响较小，而高速时对总阻力的影响则较大。从阻力的对比可以看出，与试验换算出的相当平板摩擦阻力相比，计算出的摩擦阻力稍偏小，这可能是由船体曲率变化所致，同时也说明边界层O 网格的划分还有待改进。但摩擦阻力计算与试验的误差较小，说明此计算方法对于摩擦阻力的计算具有一定的精度。总阻力在大于18 kn以后，与试验值相比均偏小，且随着航速的增加差距逐渐增大，但精度基本控制在5%以内，对于工程应用能起到一定的指导作用。

由表5 可以看出，艉倾对应的是一个最低速度，在这之前是艏倾，之后，艉倾便随着速度的增大而增大。升沉在一定速度范围内也是随速度的增大而增大。

1.4.2 压力及波形计算结果分析

图8 给出了船体表面压力分布云图在固定姿态和计及航态变化的比较（左图为固定航态，右图计及了升沉和纵倾）。从中可看出：随着在航行过程中出现艉倾，艏部球鼻艏处的吃水变浅，最大压力值降低，艏部至船舯部之间的区域压力均增大，船体艉部处的压力也稍增大，但增加值不及艏部明显。在考虑了升沉与纵倾的影响后，船体表面压力分布的准确性能更好地反映船体姿态变化的影响，从而使阻力预报值更准确。

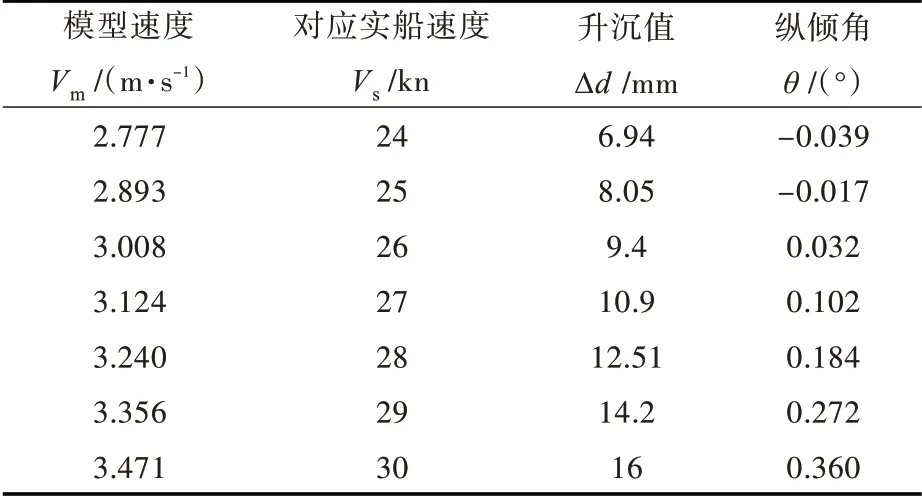
表5 各速度下的升沉、纵倾值Tab.5 The sinkage and trim results at different speeds

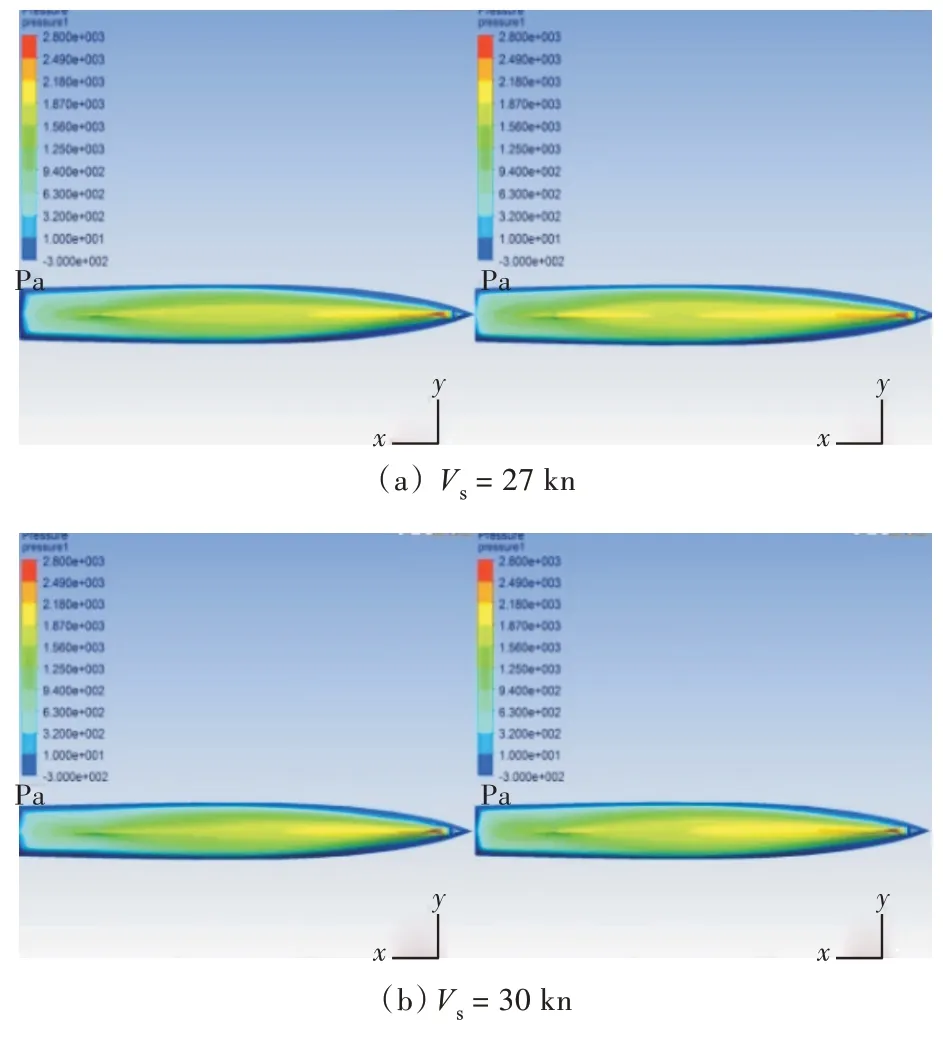
图8 船体压力对比云图Fig.8 The comparison of hull pressure contours

图9 所示分别为实船航速为24，27，30 kn 时的船模试验波面效果图。由图中可以看出波面效果逼真，峰谷清晰，艏肩波及艉部鸡尾流均能捕捉到。

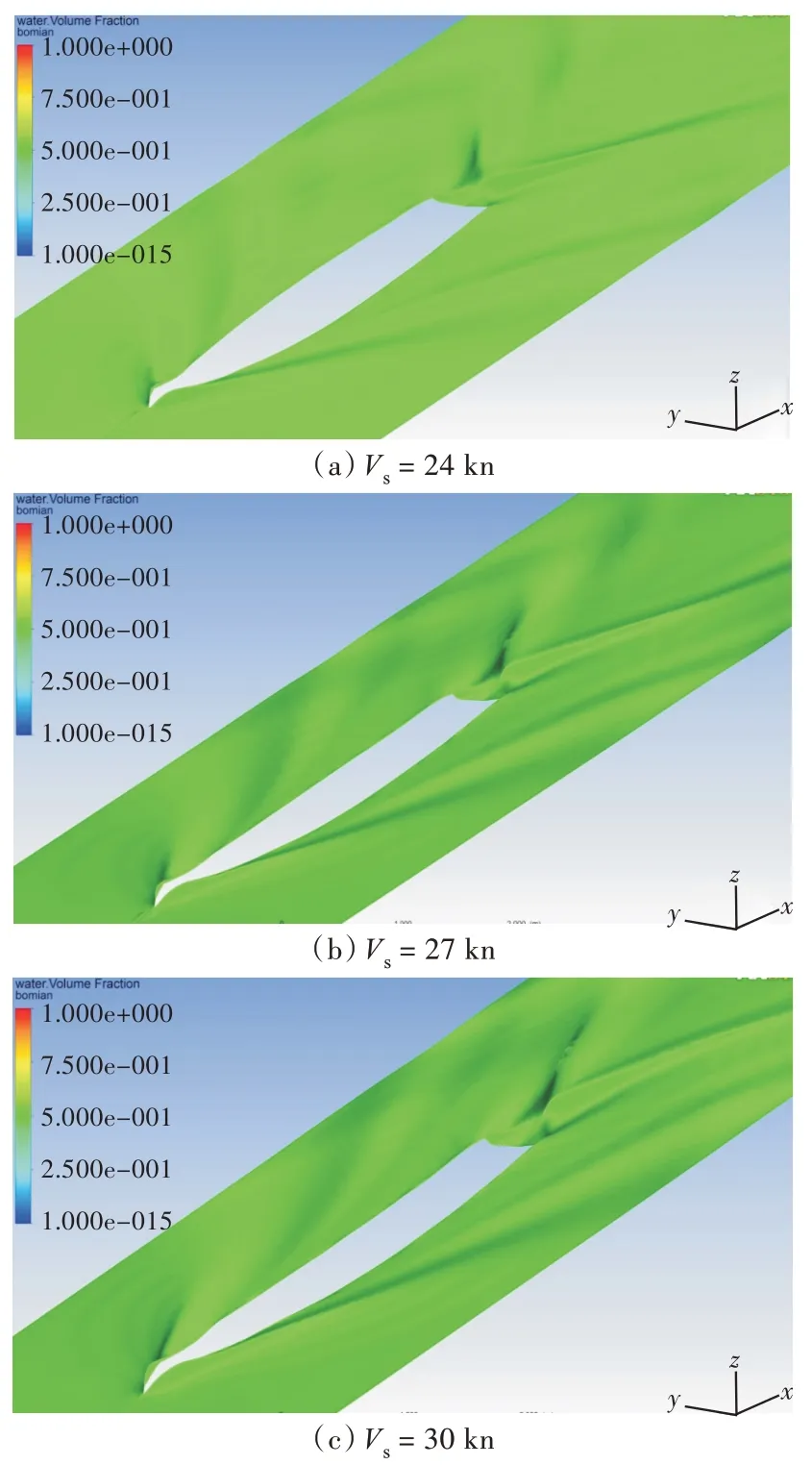
图9 波面效果图Fig.9 The effect drawings of wave

图10 所示为实船航速分别为24，27，30 kn 时的波高对比云图。分析船模试验波面效果图和波高对比云图（左图为计及升沉和纵倾，右图为固定航态）可知，计及航态后，艏、艉兴波高度增加，这也与计及航态后算得的兴波阻力比不计航态算得的兴波阻力更大的规律相符。艏部波高随着航速的增加逐渐升高，并且艏肩波有逐渐向船舯后移的现象。从船艉兴波波高对比图可以看出，船体在低速时不会产生鸡尾流，只有在高速的情况下才会产生，并且在一定速度范围内，随着速度的升高鸡尾流的长度逐渐变长。

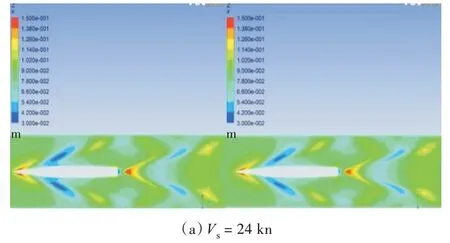
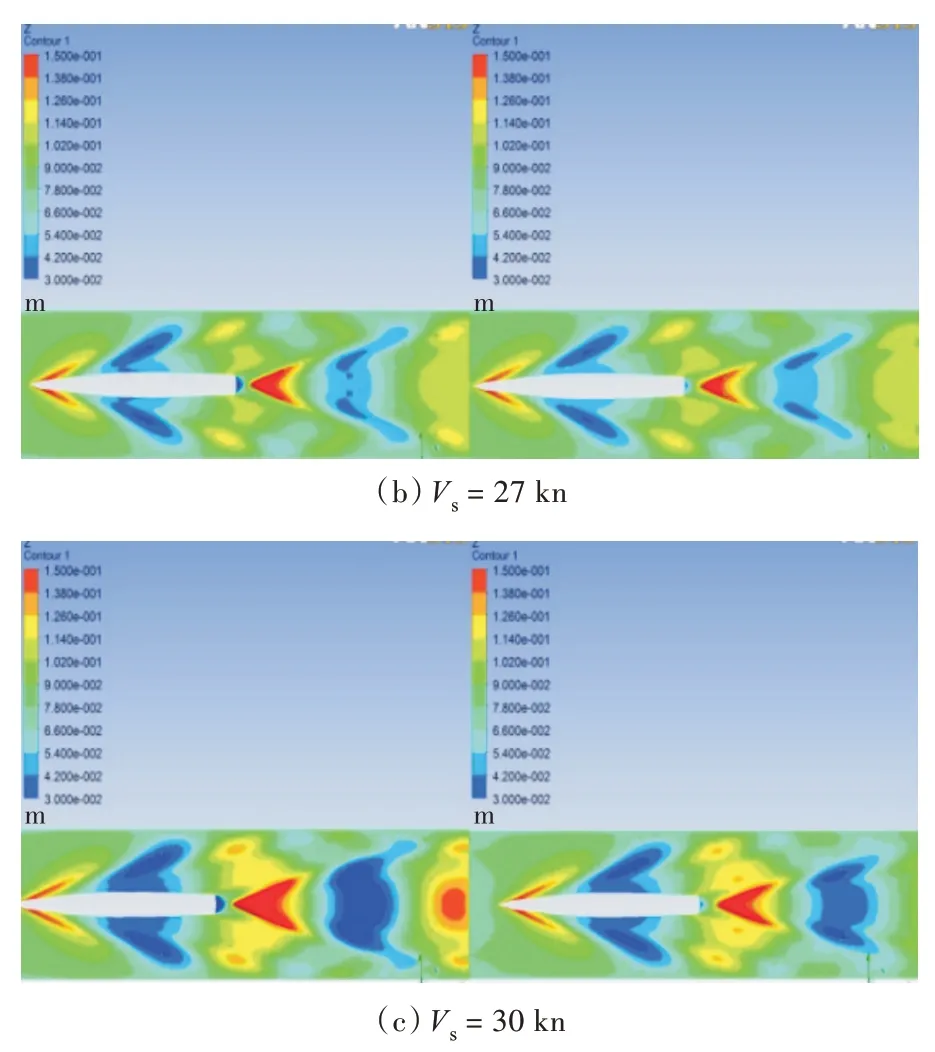
图10 波高对比云图Fig.10 The comparison of wave height contours

2 结 论

通过对计及航态的舰船阻力及自由面兴波的预报，可以得出以下结论：

1）在低速状态下，航行状态的变化对船舶水动力性能影响较小；而当航速增加到一定程度后，其阻力计算误差会达到10%以上。在计及航态的情况下，阻力计算误差降低到了5%以内，由此可知，航态对船舶水动力性能的影响不可忽略，此时，计及航态是必要的。通过数值计算的摩擦阻力、总阻力结果与船模试验值换算结果的比较，表明其符合程度令人满意，验证了本文数值计算方法的正确性和有效性。

2）本文的方法基于静态平衡法，在其方法的实现上进行了改进。每个航速下，改变航态后通常能节省1～2 次块和网格划分过程工作量，在保证计算精度的同时，大大缩短了工作时间，对实际工程应用具有积极的指导作用。

3）航态的变化对摩擦阻力影响较小，对兴波阻力影响较大。同时，在低速时，航态的变化对总阻力影响较小，在高速时影响较大。

4）在一定速度范围内，随着航速的增加，升沉值逐渐增大。艏倾和艉倾存在一个速度分界点，在此分界点后，随着速度的增大，艉倾逐渐变大。对于本文的研究，此分界点的傅氏数约为0.37。

5）艏部波高随着航速的增加逐渐升高，并且艏肩波有逐渐向船舯后移的现象。船体在低速时不会产生鸡尾流，只有在高速的情况下才会产生鸡尾流，并且在一定速度范围内，随着速度的升高，鸡尾流的长度逐渐变长。对于本文的研究，当傅氏数达到0.36 左右时会产生鸡尾流。

［1］姚朝帮. 计及航态影响的船舶阻力计算方法及其应用研究［D］.武汉：海军工程大学，2010.YAO Chaobang. Study on methods to calculate resis⁃tance of a ship taking the effect of dynamic sinkage and trim［D］. Wuhan：Naval University of Engineering，2010.

［2］DAWSON C. Calculations with the XYZ free surface program for five ship models［C］//Proceeding of Work⁃shop on Ship Wave-Resistance Computations，1979：232-255.

［3］YANG C，LÖHNER R. Calculation of ship sinkage and trim using a finite element and unstructured grids［J］. International Journal of Computational Fluid Dy⁃namics，2002，16（3）：217-227.

［4］ZHANG Zhirong，ZHAO Feng，LI Baiqi. Numerical calculation of viscous free surface flow about ship hull［J］.Journal of Ship Mechanics，2002，6（6）：11-18.

［5］曹洪建. 基于FLUENT 的滑行艇阻力计算研究［D］.哈尔滨：哈尔滨工程大学，2008.CAO Hongjian. The computation and research on resis⁃tance of planing craft based on the software FLUENT［D］.Harbin：Harbin Engineering University，2008.

［6］董文才，姚朝帮.中高速深V 型船阻力预报方法及尾板减阻机理［J］. 哈尔滨工程大学学报，2011，32（7）：848-852.DONG Wencai，YAO Chaobang. Study on resistance prediction method and resistance reduction mechanism of medium & high speed deep-Vee ship by stern flap［J］. Journal of Harbin Engineering University，2011，32（7）：848-852.

［7］倪崇本，朱仁传，缪国平，等. 计及航行姿态变化的高速多体船阻力预报［J］. 水动力学研究与进展（A辑），2011，26（1）：101-107.NI Chongben，ZHU Renchuan，MIAO Guoping，et al.The resistance prediction for high speed multi-hull ves⁃sels with consideration of hull gesture variation during voyage［J］. Chinese Journal of Hydrodynamics（Ser.A），2011，26（1）：101-107.

［8］张志荣，李百齐，赵峰.船舶粘性流动计算中湍流模式应用的比较［J］. 水动力学研究与进展（A 辑）：2004，19（5）：637-642.ZHANG Zhirong，LI Baiqi，ZHAO Feng. The compari⁃son of turbulence models applied to viscous ship flow computation［J］. Chinese Journal of Hydrodynamics（Ser.A），2004，19（5）：637-642.

［9］徐杰，俞汲，黄少锋，等.散货船阻力预报中湍流模型的应用［J］.中国造船，2011，52（增刊1）：53-58.XU Jie，YU Ji，HUAGN Shaofeng，et al. Application of Turbulence models to prediction of powering performa⁃ce for ship［J］. Shipbuilding of China，2011，52（s1）：53-58.

［10］张师帅.计算流体动力学及其应用—CFD 软件的原理与应用［M］.武汉：华中科技大学出版社，2010.

［11］王福军.计算流体动力学分析—CFD 软件原理与应用［M］.北京：清华大学出版社，2004.