对wallis 双边不等式的一个改进及应用①
2013-02-02池爱子郑米海郑鹏飞
池爱子, 郑米海, 郑鹏飞
(台州学院,浙江 临海317000)
0 引 言
Wallis 公式指的是
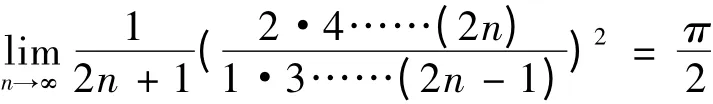
Wallis 不等式[1]指的是:对于n = 1,2,…,有
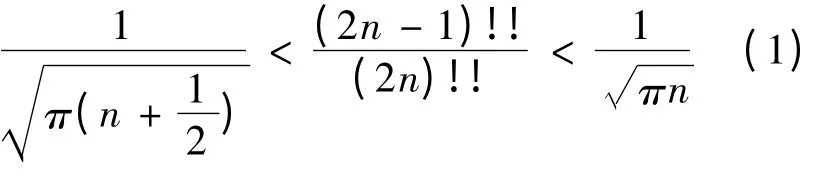
文献[2]将式(1)改进为:n = 1,2,…,有

文献[3]将(2)改进为:n = 1,2,…,有
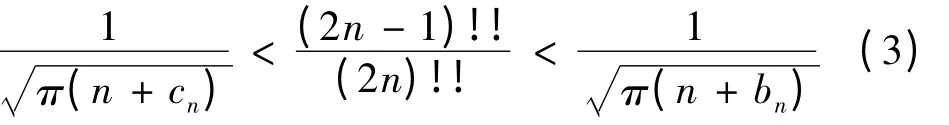
其中

文献[4]将(3)改进为:n = 1,2,…,有

其中
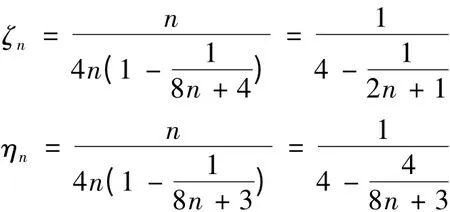
本文对式(4)中的ζn及ηn给出了更好的一个表示式.
1 定理及证明
定理1 对于n = 1,2,…,有
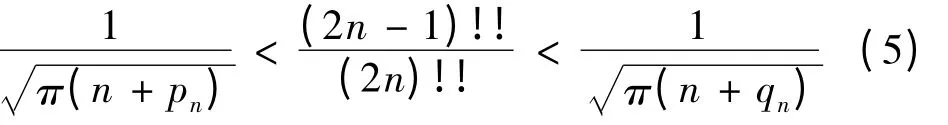
其中


由Wallis 公式,有

考察数列{xn}的单调性.为此,考虑
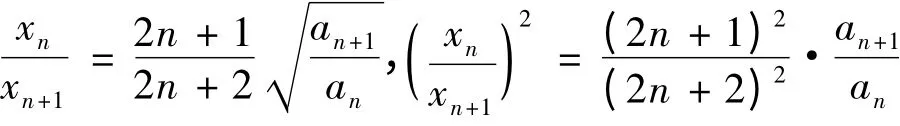
易知
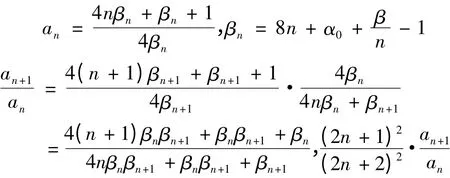
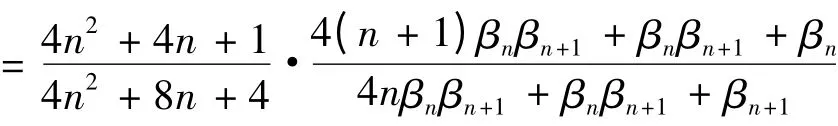
分别记上式分子,分母为An和Bn,那么

于是
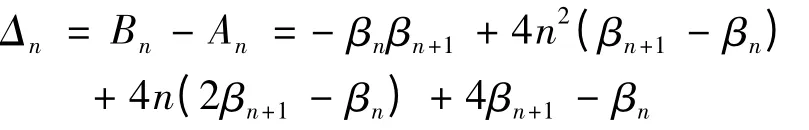
由于
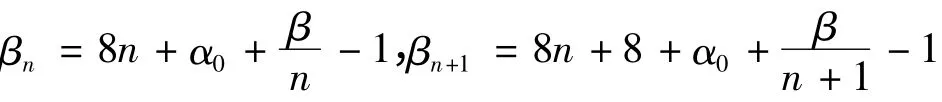
所以
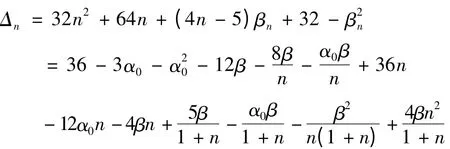
如果Δn>0,这说明此时数列{xn}是严格递增数列.
当α0= 3,
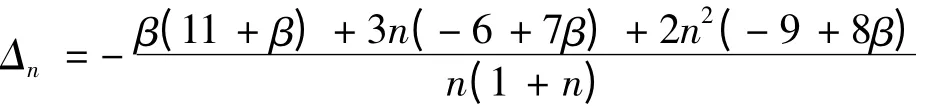
令Δn>0,此时考虑分母小于0,只要取使β(11 +β)+3n(-6 +7β)+2n2(-9 +8β)<0 最大的β即可.
令
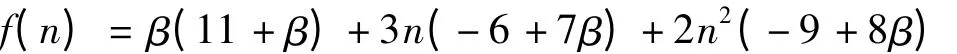
只要满足:

即可,解得

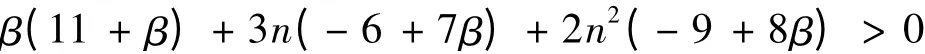
最小的β 即可.同理,只要满足
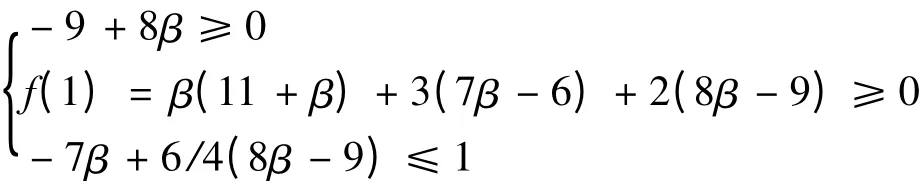
所以
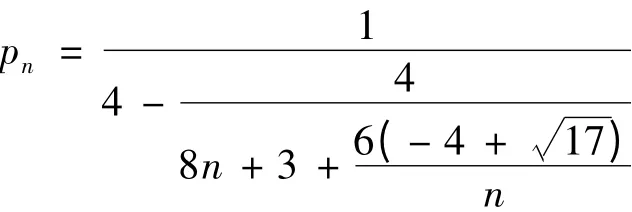
同理可得,右边
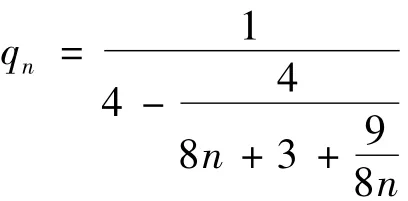
证明完毕.
2 定理的应用
2.1 Catalan 数
文献[5]给出了关于Catalan 数

的一个估计:
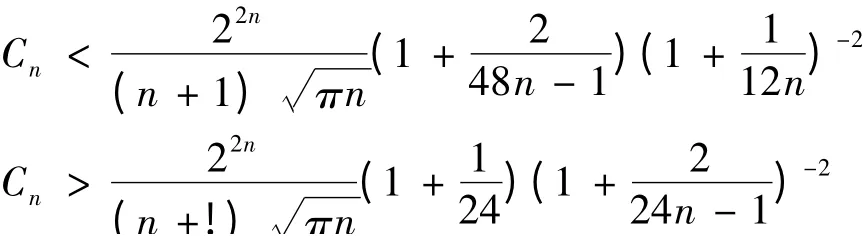
应用定理1,给出Catalan 数的另一个估计:
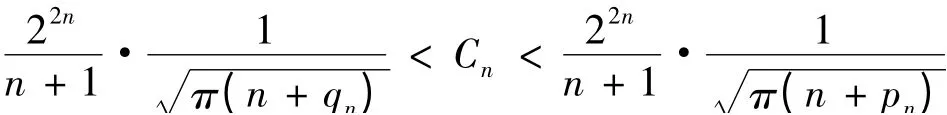
2.2 各类双边不等式的数值比较
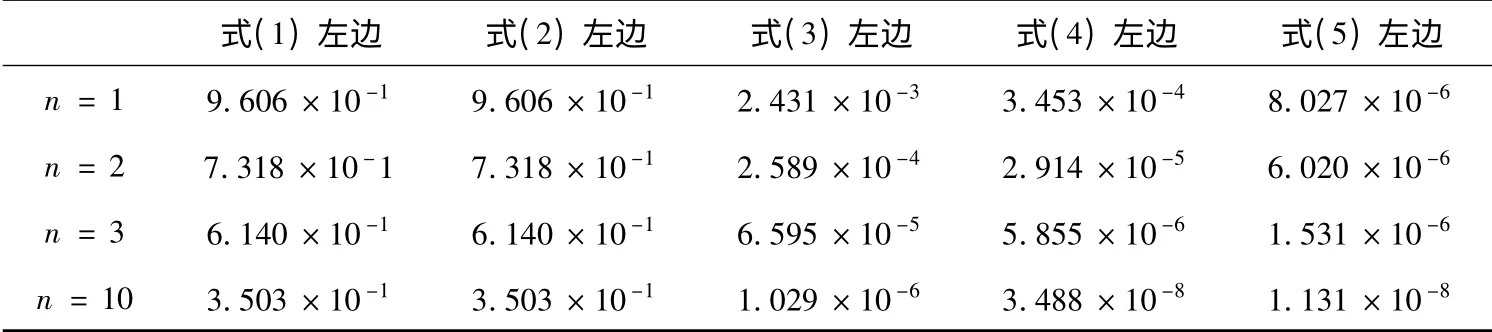
表1 各类双边不等式左边的误差比较

表2 各类双边不等式右边的误差比较
由上述表格可知,(5)式优于(1 ~4)式. 因此本文得到的结果关于Wallis 双边不等式的加强其结果更加精细.
[1] D.s.密特利诺维奇著,张小萍.王龙译. 解析不等式[M].北京:科学出版社,1987,259.
[2] Kazarinoff D K.On Wallis Formula[J]. Edinburgh Math Notes,1956,40:19 -21.
[3] 赵德钧.关于含有WaUis 公式的双边不等式[J].数学的实践与认识,2004(7),34(7):166 -188.
[4] 张国铭.关于Wallis 不等式的上界和下界[J].数学的实践与认识,2007(3),37(5):111 -116.
[5] 徐利治,罗笑南.关于含有Stirling 公式的双边不等式[J].数学的实践与评论,1999,19(3):491 -494.
[6] 匡继昌.常用不等式(第三版)[M].济南:山东科学技术出版社,2004:96 -97.
[7] 齐玉霞,周金峰.Wallis 不等式的新改进[J]. 数学的实践与认识,2009,39(8):224 -227.
[8] Zhao yue-qing,Wu qing-biao.Wallis Inequality with a Parameter[J]. Journal of Inequalities in Pure and Applied Mathematics,Volume 7,Issue 2,Article 56,2006.
