试探三维情境截获解题希望

2013-02-02谢建伟舟山中学浙江舟山316000

中学教研(数学) 2013年6期

关键词：项数试探值域

●谢建伟 (舟山中学浙江舟山 316000)

试探三维情境截获解题希望

●谢建伟 (舟山中学浙江舟山 316000)

以下这个题目曾被编入一些参考书籍，流传甚广，其实是一个错题．

1 试探问题情境

1．1 数值铺垫

例1函数y=ln(2x+2－x+m)的值域是R，求实数m的取值范围．

解值域是R的充要条件是真数2x+2－x+m能够取遍全体正数．现给m赋值，如取m=7，则

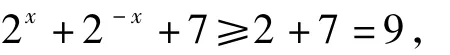
此时 y≥ln9，值域非 R．可见，2x+2－x+m=0，即 m= －(2x+2－x)应当有解．因为2x+2－x≥2，所以 m≤ －2．

点评直接去求m的取值范围，很可能出现值域为R与定义域为R的混乱．

1．2 图表引导

例2将正整数n写成二进制数时，记其中数字0的个数为I(n)．

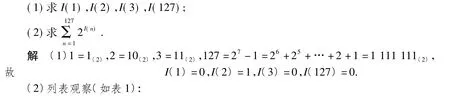
表1 对应表

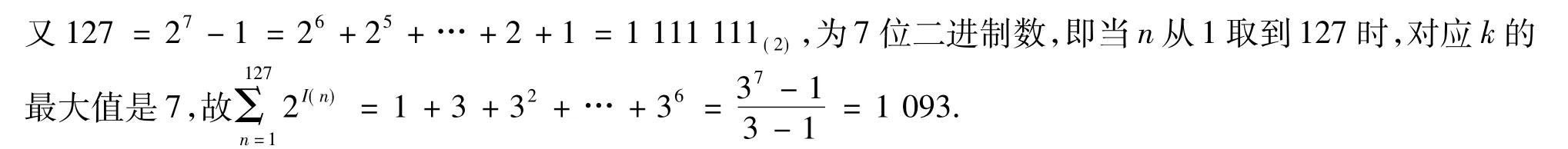
2 试探模型情境

2．1 简化模型

例3设A(1，1)，B(3，3)，试在x轴上求点P，使∠APB最大?解法1代数法．设 P(x，0)，x∈R，则

解法2几何法．如图1，过点A，B作圆O1且与x轴相切于点P，任取x正半轴上点P'，联结P'A，P'B．由圆的性质知∠APB≥∠AP'B．因为过A，B且与x轴相切的圆有2个，分别为圆O1，O2，切点P，P1(如图2)，作点P1关于直线AB的对称点P1'，可得∠AP1B=∠AP1'B≤∠APB．由切割线定理得到|OP|=．

点评模型只有在测试、比较中达到简化和完善．

2．2 还原模型

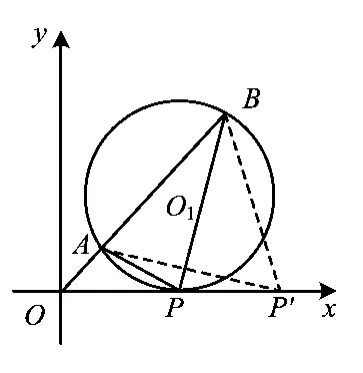
图1

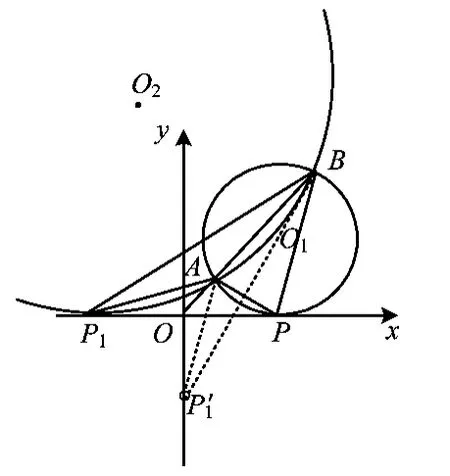
图2

3 试探难度情境

3．1 分散难点

例4记数列 a1，a2，…，an为 A，ai∈{0，1}，i=1，2，…，n．定义变换 f:将 A 中的 1 变为 1，0;A 中的 0变为0，1．设 A1=f(A)，Ak+1=f(Ak)，k∈N*，例如，当 A 为 0，1 时，A1=f(A)为 0，1，1，0．现设 A 为 1，0，1，记Ak中相邻2项都是0的数对个数为bk，求Ak的项数及bk关于k的表达式．

解分成3步来解．

第1步，读取．A有3项，因为(不论是0或1)每一次变换均将其中的项数变为原来的2倍，则可知Ak的项数为3·2k．

第 2 步，初得．A 为 1，0，1;A1为 1，0，0，1，1，0，b1=1;A2为 1，0，0，1，0，1，1，0，1，0，0，1，b2=2;A3为 1，0，0，1，0，1，1，0，0，1，1，0，1，0，0，1，1，0，0，1，0，1，1，0，b3=4;…

猜想:bk=2k－1．

答案已经有了．但这仅仅是一个猜想，离问题真正解决还有一段距离!

第3步，至理．不难发现:

(1)只有前一组数中的数对1，0才能生成后一组数中的数对0，0，即Ak中数对1，0变成Ak+1中的1，0，0，1;

(2)Ak中数对1，0的个数即为bk+1;

(3)Ak中数对1，0的个数是由Ak－1中1的个数与数对0，0的个数之和，因为Ak－1(k≥2)中1的个数等于其项数的一半，即为 3·2k－2，又 Ak－1中数对 0，0 的个数为 bk－1，所以