挖掘隐含结论 提升解题能力

☉浙江省开化县第二中学 曹嘉兴

挖掘隐含结论 提升解题能力

☉浙江省开化县第二中学 曹嘉兴

美国著名数学家和数学教育家波利亚在《数学的发现》一书中提出了“教师十诫”，其中第八诫是：“要找出手边题目中那些可能对解后来题目有用的特征——即设法揭示出隐含在眼前具体情形中的一般模型”.下面就从一道典型中考题的解法入手，谈谈如何挖掘隐含在题目的具体解法中的一般结论（不妨称之为隐含结论），然后应用这些结论解决几道与之相关的中考题，从而实现“抓住一道题，带出一串题”.

题目 （2010年宁夏卷）如图1，在△ABC中，∠BAC=45°，AD⊥BC于点D，将△ABD沿AB所在的直线折叠，使点D落在点E处；将△ACD沿AC所在的直线折叠，使点D落在点F处，分别延长EB、FC使其交于点M.

（1）判断四边形AEMF的形状，并给予证明；

（ 2）若BD=1，CD=2，试求四边形AEMF的面积.

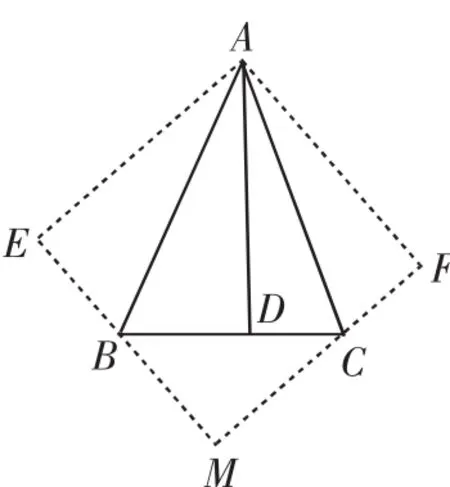
图1

从第（1）题的解法中不难看出，四边形AEMF的形状（正方形）依赖于△ABC的形状（含45°角的锐角三角形），正方形AEMF的边长就等于△ABC的边BC上的高AD，这正是本题图形的一个“有用的特征”.在第（2）题的解法中，BD和CD的具体数值（ 即BD=1，CD=2）并不重要，重要的是BD、CD与正方形AEMF的边长之间的联系，而关系式（*）中正隐含着它们之间的联系，不考虑BD和CD的具体数值就可以从关系式（*）中挖掘出更一般的结论.事实上，在Rt△BMC中，由勾股定理得BM2＋CM2＝BC2，注意到BM=EM-BE=AD-BD，CM=FM-CF=AD-CD， 于是（ADBD）2＋（ AD-CD）2＝（ BD＋CD）2.

这就得到了含45°角的锐角三角形的一个基本性质.

性质1：在锐角△ABC中，∠BAC=45°，AD是BC边上的高，则AD2=AD·BC+BD·CD.

运用性质1我们可以十分简洁地证明含45°角的锐角三角形的其他重要性质.

性质2：如图2，在锐角△ABC中，∠BAC=45°，AD是BC边上的高，在△ABC的外部作∠BAE=∠CAD，∠CAF=∠BAD分别交直线BC于E、F，则BE2＋CF2=BC2.

如同等腰直角三角形一样，含45°角的锐角三角形也是一类特殊的三角形.在近几年的各地中考试题中经常出现以含45°角的锐角三角形为背景的试题，然而在现行教材中并没有给出这类三角形的性质，致使不少同学感到难以应对.如果以上面所得到的这两个基本性质作为解题的突破口，就可以使这类题目化难为易，迎刃而解.

分析：前两个小题其实是为推导本文性质1作准备，设AD的长为x，根据本文性质1就容易列出方程，解之即得AD的长.

解：（ 1）连接OB和OC．因为OE⊥BC，所以BE＝CE．

点评：这道中考题与2010年宁夏卷基本相同，因而解题思路和方法有一定的类比性，但改为以圆为背景又有一定的新颖性.由此可以看出利用基本图形改编试题是目前中考命题的常用方法.性质1虽然是解题的突破口，但作为解答题还需记住并写出性质的详细推理过程.

例3 （2011年咸宁卷）（1）如图5，在正方形ABCD中，△AEF的顶点E、F分别在BC、CD边上，高AG与正方形的边长相等，求∠EAF的度数；

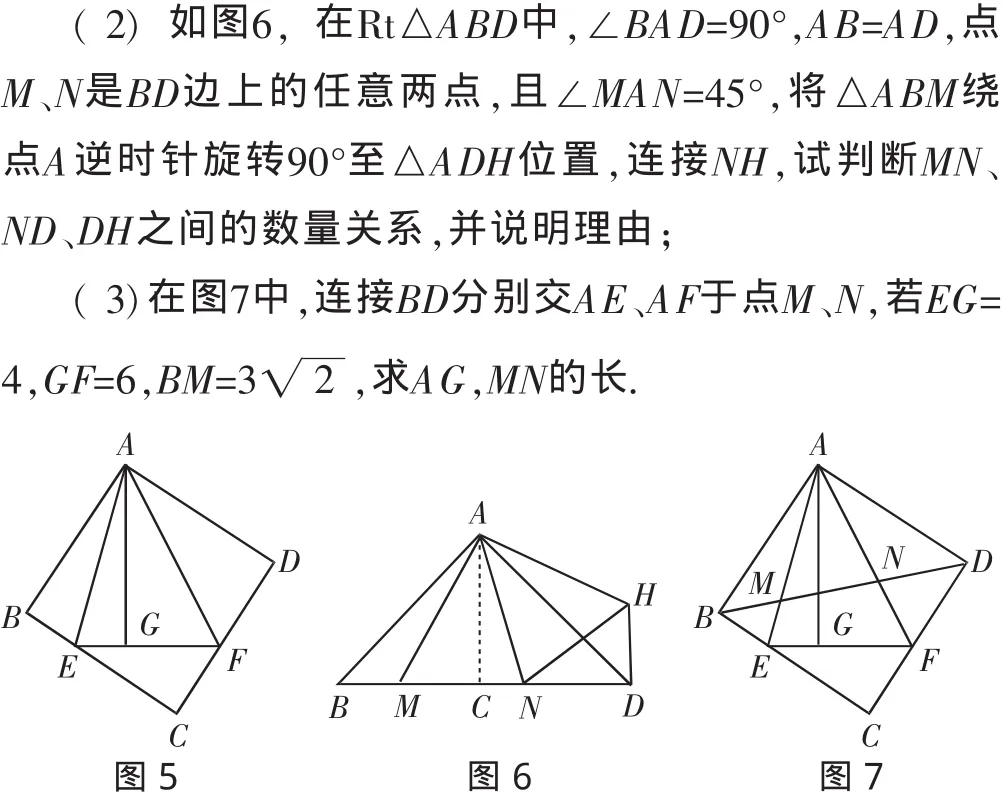
分析：从图形上看，图6的一个关键特征是45°角的顶点与等腰直角三角形的直角顶点重合，这正是本文性质2的图形特征，因此只需将本题的条件转化为性质2的条件即可得出所要的结论.

点评：第（2）小题的命题意图是利用旋转变换从图6中推导出关系式BM2+ND2=MN2（即性质2），然后利用该关系式来解决第（3）小题，但初中学生对于利用图形变换来解决几何问题并不十分熟悉.事实上，不用旋转变换直接利用性质1也可以推导出性质2.

目前，很多中考试题的设计大多采取学生比较熟悉的几何图形，以这些几何图形的基本性质为基础，通过逐步探究，不断加大难度来考查学生的分析问题和解决问题的能力.这类试题因其能充分体现《全日制义务教育数学课程标准（修订稿）》中所提出的“培养学生实践探索能力”的要求而受到各地中考命题专家的青睐，往往是各地中考试卷中的“压轴题”和“拉分题”.因此，在平时的解题教学中，培养学生从题目所给的几何图形和解法中挖掘出“隐含结论”的能力就显得尤为重要.罗增儒教授在文［3］中给出的分析解题过程的一些操作，如：看是否可以用更一般的原理去代替现存的许多步骤，以提高整个解题的观点和思维的层次；看是否可以用一个更特殊的技巧去代替现存的常规步骤，以体现解题的奇异美；看解题过程中哪一个是最实质的步骤，抓住这一步既可简化过程又可迅速推广.这些操作确实有助于我们从题目所给的几何图形和解法中挖掘出有用的“隐含结论”，进而改进解法并把它作为今后解决类似问题的突破口.总之，教会学生如何从题目所给的几何图形和解法中挖掘出“隐含结论”是教会学生“怎样解题”的一个必要步骤，也是提升学生解题能力的一个有效方法.

1.［美］乔治·波利亚.数学的发现——对解题的理解、研究和讲授［M］.刘景麟，曹之江，邹清莲，译.北京：科学出版社，2006.

2.杨世明，王雪琴.数学发现的艺术——数学探索中的合情推理［M］.青岛：中国海洋大学出版社，1998.

3.罗增儒.分析解题过程的操作［J］.中学数学教学参考（中旬刊），2009，5.

4.景敏，周静.中考试题的类比推理能力考法分析［J］.中国数学教育（初中版），2010，4.

5.李天舟.浅谈中考试题的编制方法 ［J］.中国数学教育（初中版），2012，10.FH