季节变动回归分析模型的构建与应用

李培军

(东北财经大学 统计学院，辽宁 大连 116025)

一、引 言

现代统计理论表明，某一时间序列发展水平(Y)的变动可分解为4个构成因子的影响，即长期趋势(T)、季节变动(S)、循环波动(C)、不规则波动(I)。4个构成因子之间的数量关系可表述为乘法模式Yt= TtStCtIt，或加法模式Yt= Tt+ St+ Ct+ It。时间序列分析的一项重要内容就是将这些因子从序列中分离出来，而后分别进行分析，其中季节变动是影响序列水平变动的一个非常重要的因子。所谓季节变动是指在一年时期内某些现象随着自然界季节的变换而产生的波动。研究季节变动对于分析时间序列的发展变化趋势，提高管理和决策水平具有重要的现实意义。

多年以来，观察国内外有关统计学著作或统计学教科书［1，2］可以发现，目前传统的测定时间序列季节变动的方法主要有两种:一是同期平均法或称按月平均法;二是趋势剔除法。两种方法的区别在于:前者在不考虑序列长期趋势的影响下，直接根据序列数据计算反映季节变动的指标值;而趋势剔除法则是先将序列中的长期趋势因子加以剔除，然后再测定反映季节变动的有关数值。许多学者认为，无论是同期平均法还是长期趋势剔除法，在测定时间序列的季节变动时都存在着明显的缺陷，这些缺陷主要表现在:

(1)在分离时间序列长期趋势因子和季节变动因子过程中，将季节因子当作时间序列长期趋势因子变化之后的剩余部分，人为地假设长期趋势因子变动在前，季节因子变动在后，这种假设与时间序列的变化规律不一定完全相吻合。

(2)时间序列长期趋势因子分离方法不同，导致季节变动因子指标值的计算结果不同，即存在着将季节因子包括到趋势因子中去或将趋势因子包括到季节因子中去的风险。

(3)同期平均法与趋势剔除法具有同样的缺点和不足，即对取得的测定季节变动指标值无法进行统计学的有效性检验，其可靠性得不到验证和保证，因而也就不能据此进行季节变动预测区间的推算。

针对上述传统测定时间序列季节变动方法的缺陷，本文拟采用虚拟变量回归分析的原理，将季节因子作为虚拟变量，构造含有季节因子变动的回归分析模型。利用该回归模型对序列水平进行分析，可以在分解长期趋势和其他影响因子对季节变动作用的同时进行有关的统计检验，并据此建立预测置信区间，对时间序列的未来变化趋势进行预测，从而改进传统测定季节变动方法的不足。

二、季节变动回归模型的构造

虚拟变量回归分析，是在回归分析中引入回归模型的属性变量并加以量化处理的方法和技术［3］。比如人口研究中的性别、民族、籍贯，经济研究中的地区差异、体制改革、经济政策等。由于虚拟变量取值只有1 和0 两种表现，所以也被称作0，1 变量。由此可将季节变动看成是一种属性变量，把自然界的春、夏、秋、冬4个季节变化而对社会现象产生的影响量化，即用虚实变量加以表示。取D 为季节变动的虚拟变量，并定义:

根据上述原理，就可以建立含有各种影响因子形式的季节变动回归分析模型，并可根据研究分析的目的选择使用。为方便起见，以下仅以季度数据为例，其余以周、旬、月等为时间单位或时间间隔相等的时间序列季节变动的回归分析模型可照此类推设计。

模型1:序列水平趋势的季节变动回归方程

模型2:含有线性趋势和季节变动的回归方程

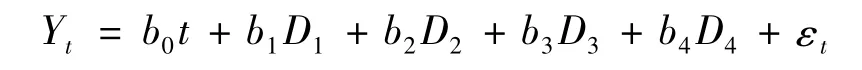
模型3:因果关系中的季节变动回归方程

模型4:因果关系中的线性趋势和季节变动混合方程

上述各回归模型中:Yt为时间序列水平值或称被解释变量;t 为时间变量;xi为第i个解释变量，i =1，2，…，k;Di为季节变动虚拟变量，i = 1，2，3，4;a1，a2，…，ak和b0，b1，b2，b3，b4为回归模型待定参数;εt为模型估计值的随机误差项。

应用上述各模型分析时间序列季节变动因子的影响具有以下几个特点:

(1)各待定参数的估计计算可借助于统计分析软件，应用计算机完成，减少计算工作量，使多因子的因素分析成为可能。同时还可以进行统计检验，获得预测值的置信区间。

(2)季节变动因子对序列水平Yt的影响作用是通过b1，b2，b3，b4来测度的，这些回归系数在模型中与其他参数同时被估计，不存在趋势值估计在前、季节变动值估计在后的问题，有利于估计程序的标准化处理。

(3)回归分析模型的综合能力较强，使传统时间序列分解因子方法的各种缺陷在回归模型3 和模型4 中得以修复，时间序列分析与因果关系分析的结合将使预测结果更接近于客观实际。

三、季节变动回归模型的案例分析

以下应用一个简单的案例说明季节变动回归模型的参数估计和统计检验过程，并与传统的季节变动因子分解方法进行对比。

1.季节变动因子的回归模型分析

设某商贸集团商品销售额如表1所示。

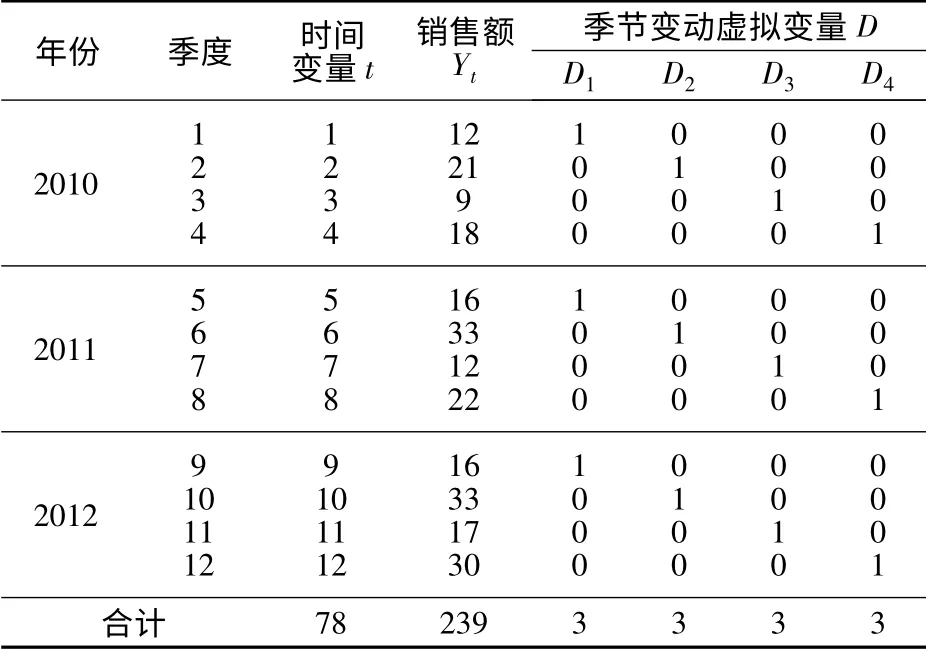
表1 某商贸集团2010—2012年商品销售额 亿元

由表1显示的时间序列变化特征可知，销售额的变动既包含长期趋势因子，也明显包含季节变动的因子。因此可以选择回归模型2。由于表1数据是来自该集团商品销售的样本数据，应由样本数据建立回归方程，使用的方程式为

将有关数据代入线性联立方程组(1)～(5)式，求得各待定参数的样本估计值:

对回归模型中的各个参数进行统计检验，给定显著性水平α = 0.01，回归方程的估计标准误差Se= 3.510，判定系数R2= 0.8832，复相关系数R =0.9398。

回归方程中各估计参数的有效性检验t 统计量为(本例为小样本，应用t 检验)

由此建立的含有线性趋势和季节变动的回归方程式为

可以认为，在α = 0.01 的显著性水平条件下，回归方程中各待定参数通过了统计的t 检验，也即该回归方程用于测定趋势变动因子和季节变动因子是有效的，符合统计理论和统计方法的要求。

依据上式计算该商贸集团2013年各季度商品销售额的预测值分别是:一季(t = 13)23.623 亿元;二季(t = 14)38.623 亿元;三季(t = 15)22.290 亿元;四季(t = 16)32.956 亿元。也可计算在一定显著性水平下的预测值区间。比如，2013年第二季度销售额在0.05 显著性水平下的预测区间为38.623 ±2.370 ×3.510，或为(30.3，46.9)。

2.季节变动因子的传统方法分析

根据表1中时间序列水平的变化特征，应用传统方法对季节变动因子进行分析。首先建立测定长期趋势因子的线性趋势方程，设T 为时间序列的长期趋势，则线性趋势方程式为

由趋势方程可求得各季度销售额的趋势值，将其与Yt比较(Yt－T)或(Yt/T)，再按同期平均以消除随机因素干扰影响，得到季节比率或季节变差，如表2所示。

传统的分析季节变动因子对序列水平影响的预测是先用趋势方程求趋势值，然后用季节比率或季节变差调整。季节比率适用于序列的乘法模式，季节变差则适用于序列的加法模式。本例用加法模式预测2013年第一季度的销售额为

类似可计算得到2013年第二、三、四季度销售额的预测值分别为37.87 亿元，21.55 亿元，32.21 亿元。这个结论虽然接近于回归模型预测的结果，但却缺少了有效的统计检验和可信度的支持。

综上可见，应用季节变动回归模型对时间序列水平变化各构成因子进行研究分析，不但是有效的，而且也是可行的。当然，任何一种统计理论和分析方法都有它的适用性和局限性，季节变动回归模型也不例外。经笔者研究认为，它的局限性主要有以下几个方面:第一，虚拟变量的陷阱问题。当选择引入的虚拟变量不适合时，将会导致模型设计的不合理，最终将导致无法求得回归模型的待定参数。第二，分析影响因素多少的问题。在回归模型中，由于各因素相互干扰极易产生回归分析的共线性问题，使得估计的回归系数不够稳定，甚至无法通过统计的有效性检验。第三，季节变动回归模型一般只适用于具有线性趋势的时间序列水平的因子分解分析，对于非线性变化的时间序列，虚拟变量的引入以及模型待定参数的估计难度较大。这些局限性还有待于在理论与实践中加以改进和完善。

［1］徐建邦，李培军.统计学［M］.大连:东北财经大学出版社，2006:305－313.

［2］徐建邦，冯 力.统计学［M］.大连:东北财经大学出版社，2011:285－289.

［3］贾俊平，何晓群，金勇进.统计学［M］.北京:中国人民大学出版社，2008:414－423.