两人问题解决中惯例的测量及其微观发生过程*

2013-01-31辛自强林崇德

心理学报 2013年10期

张梅辛自强林崇德

(1中央财经大学社会发展学院心理学系,北京 100081)(2北京师范大学发展心理研究所,北京 100875)

1 引言

问题解决作为心理学的核心议题,其研究长期以来限于单个人,较少涉及两人及以上群体。然而,这不符合大多数问题的解决是靠集体力量完成的生活现实。惯例(routines)作为组织的核心特征(此时一般称为组织惯例),是March和Simon(1958)提出的用群体问题解决思路探讨组织问题构想的例证,其研究涉及社会科学领域各个分支(Feldman &Pentland,2003;Salvato &Rerup,2011)。本研究综合以往论述(Becker,2008;Cohen &Bacdayan,1994;Egidi,1996),从操作定义的角度将惯例界定为两人或多人在面临重复性的问题解决任务时习得的、互相依赖的、可识别的、行为模式或策略。这一概念从认知和行为两个角度界定了惯例,为实验研究的开展奠定了基础。

从个体层面理解的惯例始于 20世纪 40年代Luchins(1942)有关思维定势的一系列研究。群体层面惯例的实验研究始于Cohen与Bacdayan(1994)发明的扑克牌游戏(Target The Two,简称TTT),它被评为惯例整体上缺乏实验研究大背景下“最重要的例外”(Becker,2008,p.301)。本游戏使用6张扑克牌(2♥,3♥,4♥和 2♣,3♣,4♣)由两人合作完成,格局见图1：每个玩家各持一张牌(看不到对方的牌,不允许交流),其余4张牌分两明两暗4张牌摆在桌面上。游戏目标是通过两人轮流用手里牌与桌面上的牌进行交换(可不换,但仍算走了一步),将 2♥换到目标位置。首先换牌的一方为同色玩家(她),只有当她手中的牌与目标位置的牌是同花色时(均是♥或♣),才能换目标位置的牌。另一方为同点玩家(他),只有当他手中的牌与目标位置的牌是相同点数时(均是2,3或4),才能换目标位置的牌。换其他位置的3张牌无任何限制。换牌后,保持牌原先明暗不变。每完成一局小组将获得一定奖励(如 1美元),但每走一步要扣掉一定奖励(如 1美分),游戏结束后两玩家将获益平分。游戏一般约进行40局。1996年Egidi将现场进行的游戏改为计算机版。

Cohen和Bacdayan(1994)认为本实验模拟了组织生活的一些基本特征：同色和同点玩家的限定造成能力的不对称以及对能力和角色分配的可能性;玩家手中的牌及桌面暗牌造成了信息的不对称和不确定;总体来说,通过合作两个玩家都能获益,但当合作失败时两人的效率还不如一个人的效率高;各小组成员的角色会随着各小组发展出有效的游戏方法而逐渐构建起来;这种学习过程形成了一个微小而短暂的组织。

图1 TTT游戏的初始牌局

游戏中惯例的测量通过四个判定指标实现(Cohen &Bacdayan,1994)：(1)可靠性增加。这一指标体现了组织处理问题能力的提高,可用所有玩家玩每局游戏时所需步数的变异性体现。(2)速度增加。面对陌生环境时惯例化的行为要比深思熟虑的决策快。它可用玩家完成游戏所用时间随局数增加而减少来体现。(3)重复的行动序列。构成惯例的诸多行为是随时间重复的,玩家会逐渐从“一次考虑一步”发展为一次考虑一个“组块”。(4)偶尔的次优性。游戏中玩家会被锁定于某行动序列,即使有更有效的方法也不去采用。此外,Egidi(1996)通过关注目标位置牌的移动构建了本游戏的问题空间图(图2),提出了验证惯例的第5个指标——基于特定策略的反应模式。

图2 TTT扑克牌游戏的问题空间图

作为一个界定良好的问题,TTT扑克牌游戏获得了很多赞誉,但它并未像问题解决研究中的汉诺塔任务那样得到广泛应用,个案近年来仍是惯例研究的主流(De Boer &Zandberg,2012;Labatut,Aggeri,&Girard,2012)。这一是由于TTT扑克牌游戏任务规则及完成过程复杂,使其超过两人便难以进行实验操纵和结果解释。例如,王建安和张钢(2008,2010)开发的三人版任务中,问题空间图呈网状复杂结构。二是,验证和描述惯例的各项指标均可继续细化和改进：(1)可靠性。这本质上代表问题解决效率的提高。原先四分位差指标虽具合理性,却非原始数据,用玩家每局所用步数及每局的获益的变异可能会更直观地体现问题解决效率的提高。(2)速度。这本质上是从时间角度体现问题解决效率提高。除用被试组完成每局游戏所用平均时间外,还可用每组被试完成每局游戏所用总时间及每一局游戏的平均步时来刻画。(3)重复的行动序列。可尝试用量化方法描述重复的行动模式,并探索被试每步换牌选择的位置上的行为固着。(4)偶尔的次优性。可尝试通过个案分析更为直观地展示。

与实验研究进展缓慢形成对比,惯例在组织行为学、管理学和经济学领域的研究取得了丰硕成果并出版了《组织惯例手册》(Becker,2008),但其研究中仍存在如下悬而未决的问题：(1)惯例的意识性。惯例是自动、无意识的(Cohen,1991;Stene,1940),还是需要意识努力(Feldman,2000;Feldman&Pentland,2003)的？当前存在两派截然不同的观点。(2)惯例的稳定性。基于生成观理论(Feldman &Pentland,2003;Pentland &Feldman,2005;Pentland,Feldman,Becker,&Liu,2012),惯例同时具有稳定性和变化性,这可解释组织技术及知识创新、演化、动态能力的形成、组织适应等。然而,这些大多基于理论推断,缺少实验研究的支持。(3)惯例与陈述性知识的关系。自Cohen和Bacdayan(1994)证实惯例作为程序性记忆存储后,研究者们大多在这个框架下讨论惯例的特点,很少关心惯例形成和变化过程中陈述性知识的作用。王建安和张钢(2008)证实带有陈述性知识特征的图式对惯例具有重要影响,但未说明惯例本身是否含有陈述性知识的成分。

上述问题集中体现为当前缺乏惯例从无到有产生过程的研究。受研究方法的局限,当前大多研究只能对已存在的惯例进行分析,无法分析其形成过程。心理学中用于探测认知变化的微观发法使之成为可能。微观发生法作为一种特殊的发生法和纵向研究方法,可以细致地刻画学习过程如何发生,现已广泛应用于探测问题解决中几天、几周内的认知和策略变化(辛自强,林崇德,2002;Kuhn,Goh,Iordanou,&Shaenfield,2008;Luwel,Siegler,&Verschaffel,2008)。惯例作为问题解决中形成的策略,存在从无到有的产生过程;同时,计算机可以记录TTT扑克牌游戏中的所有变化。因此,理论上微观发生法的分析思路可以探测惯例产生过程。然而,微观发生法本质上只是一种精细的实验设计和数据分析的思路,它相当于一个放大镜,将认知变化的路线、速率等清晰地呈现于人们的视野中。但是,放大镜具体应聚焦于多局游戏(相当于重复进行了多次问题解决)的哪个位置,还需要相应理论的指导。Kamiloff-Smith(2001)提出的表征重述理论可能满足了这种需要。本理论认为,知识或策略的获得是个体对原有表征不断进行重组、建构,逐渐把行为程序中存储的内隐知识转变为外显知识,并为认知系统其它部分所利用的过程。受这一理论启发,可将多局 TTT扑克牌游戏划分为不同阶段,分析每个阶段内行为的变化。

综上,本研究的目的一是对基于 TTT扑克牌游戏的两人问题解决中的惯例进行验证和描述,将Cohen和 Bacdayan(1994)提出的指标进一步完善;二是采用微观发生法的设计和分析思路,对惯例从无到有的产生过程进行描述,解决以往研究中有关其意识性、稳定性及与程序性知识关系的争议。

2 研究方法

2.1 被试

选取某大学本科生70名,由计算机随机分为35组。其中,男—男、男—女和女—女组的人数分别为8、14、13。经确认,所有被试均未参加过类似测试。

2.2 实验平台及实验设计

本测验由专业的程序员采用 ASP.NET和 C#语言在windows server 2008环境下进行程序开发,使用 IIS7作为网络服务器开发相应的测验及操控平台。测试时,被试注册并学习完游戏规则后,随机进入某个 2人房间完成测试(界面如图3)。电脑自动记录每个玩家每步换的牌、所用时间以及每局各组得分、步数和时间。

按照微观发生法的设计要求,测验任务需多次重复。本研究基于 TTT扑克牌游戏的问题空间图(图2),将初始位置的扑克牌固定为 4♣(保证完成每局游戏的最优策略相同)设计了40局游戏。为控制 2♥所在位置对初始牌局难易程度产生的影响,对 2♥出现的 5个位置(除目标位置外)进行了平衡,即每个位置均出现 8次。此外,借鉴 Egidi(1996)的设计思路,40局中设置5局重复的游戏模板,将前5局出现的模板在后5局重复出现。被试组每完成一局游戏获得100分,每走一步扣2分。测验完成后,按照每组获益给予被试 5～15元不等的奖励,并让其填写包含个人信息和实验信息的问卷,同时反馈自己是否意识到所采用的策略及与组员配合的过程。

图3 TTT扑克牌游戏界面

数据以 Excel格式从数据库中导出后,将每条记录以小组为单位进行整理：计算每组被试每局所用的步数、时间、得分、所用策略(据目标位置牌的移动整理)及行动序列。其中,被试换牌的行动序列与前人一致,用如下符号刻画(Bonini &Egidi,1999;Cohen &Bacdayan,1994;Egidi,1996)：U—换明牌;C—换同色玩家左侧的暗牌;N—换同点玩家右侧的暗牌;T—换目标位置的牌;P—过牌不换。

3 结果与分析

3.1 各组被试表现的描述

首先,整体来看,35组被试在40局游戏中平均每局游戏获得 86.84分,7步完成,用时 2292.50s,每步用时8.77s。由策略选择的事后分析可知,35组被试大多应用 4♣2♣2♥(平均 22.00 次)和4♣4♥2♥(平均15.49次)两种最优策略,其他目标位置牌需经 3次(如 4♣3♣3♥2♥、4♣3♣2♣2♥)、4次及以上(4♣2♣3♣3♥2♥、4♣4♥3♥3♣2♣2♥)变换的次优策略平均应用2.6次。通过对每个游戏模板上被试表现的描述发现,40个游戏模板中,被试组在模板9上表现最好,在模板2上表现最差。

为测查是否经过多局反复解决类似问题,各被试组解决问题的效率得到了提高,研究采用事前事后设计的思路对前后5局游戏各项指标进行了对比,结果见图4。

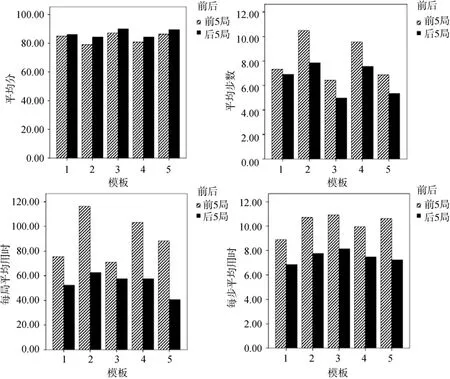
图4 前后5模板每局得分、所用步数、每局用时、每步用时的差异

在得分上,前 5局总分显著低于后 5局(

=−3.05,

＜0.01),但只有模板2及3上前后5局的差异达到了显著性水平(

=−2.13,

−2.27,

＜0.05);在所用步数上,前后5局总分差异不显著(

=−0.88,

＞ 0.05),但模板 2、3、4 上前后 5 局的差异显著,

＜0.05;在每局所用时间上,前5局显著高于后5局(

=3.96,

＜0.001),但只在模板 2(

=3.11,

＜0.01)和4(

=2.71,

＜0.05)上达到了显著性水平;在每步的平均用时上,前5局显著高于后5局(

4.23,

＜0.001),且每个模板上的差异均达到了显著性水平。表1为每个模板上前后 5局所用策略的变化数。后5局与前5局相比,4♣2♣2♥策略的使用增加了18次,4♣4♥2♥策略的使用减少了7次,其他策略的使用减少了 11次。对上述差异的卡方检验表明,只有其他策略的使用次数达到了显著性水平,χ=4.48,

＜0.05;4♣2♣2♥和 4♣4♥2♥策略的使用次数前后5局差异均不显著,χ=0.41/ 0.01,

＞ 0.05。

3.2 TTT扑克牌游戏中的惯例

由上述结果可知,重新设计后的40局TTT扑克牌游戏中可能存在惯例,下面继续按照前述的 5个指标对惯例进行系统验证和描述：

表1 各模板前后5局采用策略的变化数

(1)可靠性增加。分别以玩家完成每局游戏所用的步数和每局获益为因变量,以局数为自变量进行回归分析,结果表明,随着局数的增加,被试组完成每局游戏所用步数逐渐减少,

=−0.10,

=−3.87,

＜0.001;每局的获益逐渐提高,

=0.10,

=3.83,

＜0.001。(2)速度提高。分别以被试组完成每局游戏所需的时间和平均步时(每一局游戏的所用时间除以所用步数)为因变量,以局数为自变量,进行回归分析,结果表明,随着局数的增加,被试组完成每一局游戏所用时间和完成每一步的平均时间均在减少,

=−0.16,

=−6.05,

＜0.001;

=−0.11,

=−4.07,

＜0.001。(3)重复行动序列。对每组被试完成每局游戏的行动序列进行总结发现,在1400(40×35)局游戏中,以第1步换牌位置为起点,存在如表2所示的典型模糊行动序列。例如,“CC*T*T”代表第1步时同色玩家选择换右上位置的牌,之后同点玩家也选择换右上位置牌,中间经过数次变换,两位玩家均换了目标位置的牌而达成目标。由表可知,不论玩家第1步选择换哪个位置上的牌,都存在一定的行为模式。对上述5类模糊行动序列次数的卡方检验表明其差异达到了显著性水平：χ=262.11,

＜0.001。

除上述模糊的行动序列之外,在所有 1400(35×40)局游戏中,被试组完成每局游戏的完整行为模式也存在重复,表3为应用次数超过20次的行为模式。例如,“换目标位置牌→换明牌→过牌→换目标位置牌”(即 TUPT)的行动序列作为独立策略完成了54局游戏,还作为“组块”在153局游戏中出现。

(4)基于特定策略的反应模式。由上述分析可知,各被试组对4♣2♣2♥和4♣4♥2♥两种最优策略具有不同程度的依赖性。

(5)偶尔的次优性。对每个游戏模板上采用策略的分析发现,被试一旦认定了某策略,即使有更好的策略也不会采用。以模板 19(图5)为例,若被试组选择 4♣4♥2♥策略,5步即可快速完成(PUPTT)游戏;若选择4♣2♣2♥策略(共15组),则需先寻找暗牌 2♣,这可能会造成多次反复并应用次优策略(2组),进行8步以上甚至多达到14步之多的换牌。

由上述分析可知,在 TTT扑克牌游戏为任务的两人问题解决中存在明显的惯例现象,其主要体现为对两种最优策略和不同行动序列的坚持。在此基础上,研究继续采用微观发生法的分析思路探讨惯例的产生过程,尤其是策略的形成和变化。

表2 重复的行动序列模式

表3 每局游戏行为模式的应用次数

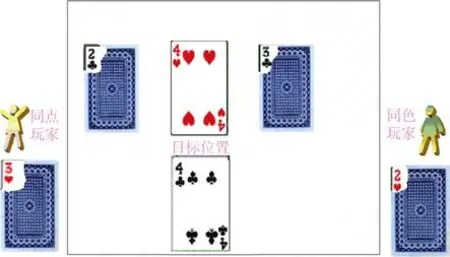
图5 模板19的初始牌局

3.3 TTT扑克牌任务的阶段划分

依据前述的表征重述理论(Kamiloff-Smith,2001)将40局游戏划分为4个阶段,每阶段各被试组表现见表4。由表可知,四阶段各项指标的变化模式是统一的：得分上四个阶段依次升高;每局所需步数、每局所用时间、每步所用时间上四阶段依次降低。

表4 不同阶段35组被试的表现

为了检测上述各差异是否达到显著性水平,分别以四项指标为因变量,以阶段为自变量进行单因

表5 不同阶段35组被试的表现的方差分析

素重复测量的方差分析(其结果与单因素随机区组设计完全一致)。由表5可知,阶段主效应在四个因变量上均达到了显著性水平(

＜0.001)。进一步事后检验(LSD)结果表明,阶段Ⅰ的各项指标与其余3个阶段差异显著,但3个阶段之间均无显著差异。

由上可知,被试的各项行为指标在不同阶段均发生了变化,下面继续采用微观发生法的分析思路从变化的路线、变化的速率、变化模式的多样性、变化的来源四个方面探讨惯例产生过程的特点。

3.4 变化的路线

3.4.1 四个阶段策略使用率的变化

图6为四个阶段不同策略的使用频率,其计算方式为本阶段内某策略的使用次数除以 350(35×10=350)。由图,虽然两最佳策略的使用率分别由阶段Ⅰ的56%、33%上升到阶段Ⅳ的59%、39%,但对次数的卡方检验表明,上述差异并不显著,χ=2.20,χ=6.90,

＞ 0.05。其他策略的使用率由阶段Ⅰ的11%持续下降为阶段Ⅳ的2%,且对次数的卡方检验表明,上述差异在四阶段内达到了显著性水平 χ=30.80,

＜0.001。

图6 不同阶段策略使用频率的变化

3.4.2 四个阶段行为模式的变化

图7为四个不同阶段第1步同色玩家换5个位置牌的次数变化。第1步选择换右上位置的牌的各种行为模式(C)的次数从阶段Ⅰ的 35%下降到阶段Ⅳ时的 30%,卡方检验表明,其差异达到了显著性水平,χ=55.39,

＜0.001。其余行为模式的使用次数虽然在四个阶段不断变化,但差异均未达到显著性水平。

图7 不同阶段行为模式使用频率的变化

3.4.3 策略变化的顺序——聚焦于阶段Ⅰ

与策略和变化路线密切相关的问题是：被试组的行为模式及其使用策略是按照怎样的先后顺序出现的？又经历了怎样的变迁？这其中最主要的问题是两人如何配合确认问题解决的最优策略并坚持下去。由表4可知,各被试组行为指标的变化主要集中于阶段Ⅰ。因此,研究通过分析阶段 10Ⅰ局游戏中各组被试的策略表现尝试回答上述问题。经分析,第1局游戏时,有 17组被试采用了4♣2♣2♥策略,12组采用了 4♣4♥2♥策略,6组采用了其他策略。之后,35组被试策略的使用分为如下情况：

①坚持第1局应用的策略不变。10局中坚持多少局才算真正在应用此策略而非偶然或猜测？这可转化为这样一个概率问题：在 10次重复的选择中,被试每次在 3个不同策略选项中选择某策略的次数为多少时,才证明他不是猜测？利用二项分布原理,可计算出偶然选择某策略的概率,其公式为：

根据以上计算的每局游戏猜对某策略的概率,可用概率加法求得猜对本策略 7题以上的概率为0.018549,不足5%,因此,10局游戏中,有7次及以上选择某策略才算真的在使用某策略,不是偶然或者猜测,作此结论尚有95%犯错误的可能。通过分析,共有 8组被试在阶段Ⅰ坚持应用了 4♣2♣2♥策略;2组被试应用了4♣4♥2♥策略。

②将第1局应用的策略调整为其他策略。应用上述方法可以计算出除第1局外的9局游戏中选择某策略6局及以上不是猜测,而是对策略的坚持。通过分析,共有 6组被试是这种情况,均为由4♣4♥2♥或其他策略变为 4♣2♣2♥策略。

③偏向两种最佳策略之一。偏向是指将某些其他策略视为两最佳策略的变式后,10局中有 7次,或9局中有6次采用某最佳策略。例如,4♣2♣3♣2♣2♥策略可视为 4♣2♣2♥策略的变式,因为二者均由同点玩家用2♥与目标位置的2♣交换结束任务。经统计,有8组被试明显偏向 4♣2♣2♥、3组被试明显偏向 4♣4♥2♥策略。

④两种最佳策略并存。共有6组被试属于这种情况。第25组被试两种策略各使用5次,且无其他策略;第33组被试除前2局采用其他策略,两策略各使用4次;第13、14、23和26组被试将其中其他策略视为不同变式后,两策略的使用次数相等。

⑤无固定策略,一直处在摸索中。共有2组被试属于这种情况。

3.5 策略变化的速率

通过上述分析可知,四个不同阶段被试组采用的策略在不断变化,这种变化的速率如何？这可通过分析相邻两个阶段内3种策略使用次数的变化及其差异检验来回答。由表6可知,只有阶段Ⅰ和阶段Ⅱ中4♣4♥2♥策略的增加及其他策略的减少达到了显著差异：χ=4.80,

＜0.05;χ=9.31,

＜0.01,其他相邻两阶段三类策略的使用次数均无显著性差异。这表明策略的变化在阶段Ⅰ和阶段Ⅱ间最为明显和迅速,其余阶段间相对隐蔽和缓慢。

3.6 策略变化模式的多样性

由上述策略变化路线的分析可知,TTT扑克牌游戏中策略变化模式存在多样性。通过每组被试在四个不同阶段采用策略的变化,可以全面分析策略变化模式的特点,结果见表7。

表6 35组被试不同阶段策略使用次数的卡方检验

通过上述计算猜测率的方法,表7中“固定”的涵义为10局游戏中,7局及以上选择了某策略;“调整”的涵义为10局中坚持某策略不到7局;“偏向”的涵义为将一些其他策略视为本策略后,10局中有7局使用本策略或者9局中有6局使用本策略;“并存”的涵义为两种最佳策略各采用 5次或去掉其他策略后,使用两种策略的次数相等。由表可知,35组被试在四个实验期间表现出 33种变化模式,可谓复杂多变。

3.7 策略变化的来源

通过事后访谈可知,TTT扑克牌游戏后期几乎所有被试组均意识到了两人所采用的策略,这些策略经由双方互相磨合形成,磨合的过程是策略和行为模式变化的主要原因。

(1)策略形成的方法

第一,心中有明确的策略,主动创造条件配合对方或等待机会。例如,有玩家说：我要拿红心2,等待对方把梅花 2放在目标位置去换以完成游戏(01-D)。可见,作为同点玩家的他脑中有清晰的4♣2♣2♥策略。再如,还有玩家结合自己身份主动配合对方：因为我是同点玩家,达成目标的概率低于同色玩家,故基本给对方制造条件,让对方尽早达到目标,除非能在明牌中一眼看出我可以达成目标(11-S)。显然,他拟采用的是4♣4♥2♥策略。

第二,通过揣摩对方的行为模式,适时调整配合策略。有玩家通过观察,确定了“被动”配合策略：多做几局就发现他比较喜欢先把草花 4换成红的,如果我的第一张牌不是 2,我会先换它成草花 2或者红 2,如果我手上是这张牌,一般都懒得换,直接等对手换到合适的牌(25-S)。还有玩家描述了自己复杂的推理过程：通过同色玩家出的第一张牌,来暗示“目标位置”是用同色完成,还是同点完成,这就需要同色玩家先有计划,哪种方法用的步骤最少。然后同点玩家要通过同色玩家的换牌推测他的计划,确定谁来完成最后一步,谁来做辅助(32-S)。

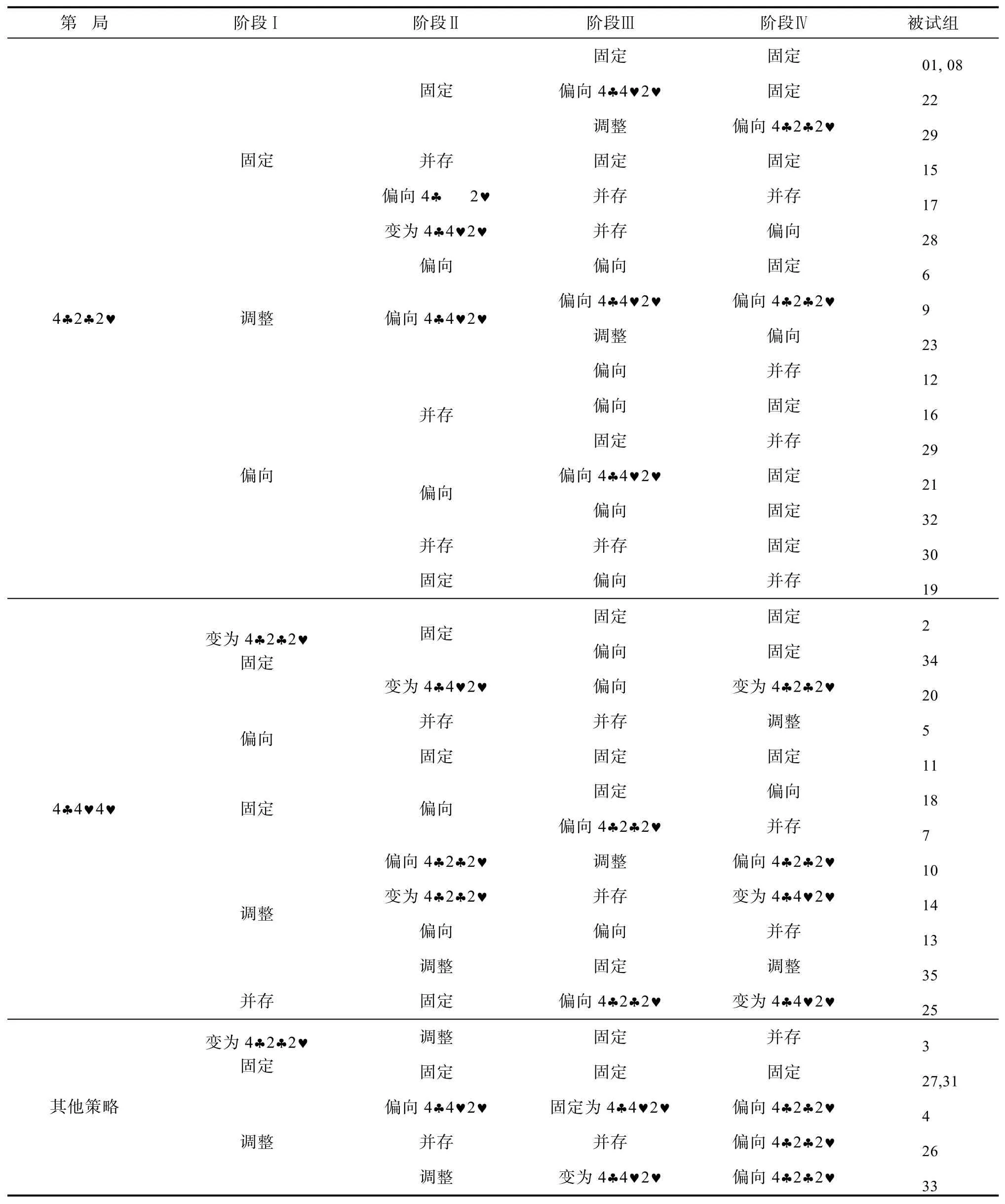
表7 35组被试在四个阶段所用策略的变化模式

第三,过牌(P)的暗示作用。有玩家通过过牌暗示对方自己手里有关键牌,让对方配合自己：如果我手里有红 2,我会不换牌,暗示让对方换红牌到目标位置玩家(03-S)。还有玩家通过观察牌面变化和反应时间推测对方过牌的原因：如果看到牌没有什么变化,说明红二已经出现。这个时候,如果同伴点了对手继续,那自己就知道该怎么做了(04-D);如果对家一直“过”(很快地轮到我)这就说明,他手中有目标位置的牌了。

第四,通过明牌(U)提示对方,进行无声交流。如同点玩家07-D这样处理关键牌：如果手上有红心2但是自己又不能达到目的,就放在亮牌位置,方便对方换取,完成任务。又如13-S的描述：如果一方拿到目标牌暂时无法实现任务时,就把目标牌放在名牌的位置,看谁更快完成谁就先拿目标牌。编号为12-D的被试没有关键牌时也会采用这种方法：开始的时候,我们会先换明牌,以让对方了解自己手中的牌。

(2)策略变化或配合不当的原因

第一,规则的熟悉及熟练应用需要时间。开始几局,有玩家对自己的身份特点应用不熟练：游戏开始几道题不是很默契,总是忘记自己扮演的角色(10-D);也有玩家总是控制不住竞争的心理：刚开始的时候总觉得我和同伴是竞争对手的关系,没有相互配合。这正如某玩家(09-D)的总结：这是一个必经的过程,我觉得这个测验分为三个阶段,首先是熟悉游戏和探索配合方法,然后再去寻找策略,最后基本稳定。

第二,过于“理性”导致的配合不良。许多玩家会按照初始牌局特点,设想不同境况下的不同反应,如对方不能跟上自己的节奏就会出现配合不流畅的情况。如编号为04—S的玩家描述了4种情况下该如何反应：谁手里有红桃2的话就先不走,手里没有红桃2的人就尽量给对方做牌,把目标位置换成对方能换的牌,然后让对方来走。如果这两点都不符合的话就换两张暗牌。如果出现了不太配合的情况就把红桃 2换到明牌上,作为一个提示,告诉对方手里是什么牌,这样就可以形成配合了。

第三,双方想法不匹配。有的是“太想配合”而导致的“不配合”：我们没有形成固定的策略,有时都想给对方提供换牌的可能,结果弄巧成拙(12-S);有的是对双方的分工有不同理解,如08-S所述：双方需要在游戏当中形成分工,一个人做牌(注：将目标位置换成 2♣或 4♥),一个人胡牌(注：用 2♥换牌)。但是同色应该比同点容易胡牌,但我的队友好像没太意识到,总在等着我给他做牌。还有对双方地位的定位存在偏差：开始时,主动置换明牌的一方,是有策略、在合作中居于领导和主动地位的,另一方就是跟随者,这样就容易合作。如果双方在合作中争夺主导权,会走很多冤枉路(12-D)。

4 讨论

4.1 TTT扑克牌游戏为依托的两人问题解决中的惯例现象

惯例这一概念源于组织、管理和经济学文献(Becker,2007;March &Simon,1958;Nelson &Winter,1982;Stene,1940),可以视为一种群体思维定势(Cohen &Bacdayan,1994)。本研究在重新设计的40局TTT扑克牌游戏中,证明了这一现象的普遍性。

研究首先采用事前事后设计和分析的思路探讨了前后 5局模板上被试组表现的差异,这相比Egidi(1996)的研究将5局重复模板放到40局的中间且未对结果进行数据分析,是一种改进。研究发现,经过30次重复性解决同一类问题,被试组在同一模板上问题解决的效率以及所应用的策略均发生了变化(图4)：第一,对每个模板上前后5局的对比表明,在每局的得分、所用步数和步时上,前后5局的差异在模板2、3、4上比较明显;在平均步时上各个模板上差异均非常显著。这主要是因为模板1和 5相对简单,不论是否形成惯例,只要理解了游戏规则,完成并不难。平均步时这一指标对问题解决效率的体现更为明显,它反映的是被试进行每一步换牌的思考时间。如果已经形成惯例,虽然完成每局所用总时间上可能变化不大,但每一步动作的目的性会更明确,因而,降低的幅度也最明显。第二,将前后 5局各视为一个整体,对比其各项指标前后5局的差异后发现,在反映问题解决效率的各项指标上,均是后5局好于前5局,具体体现为总得分的增加、完成每局总时间的减少,和完成每步总时间的减少,但在完成每局的总步数上却无显著差异。这说明,问题解决效率的提高,集中体现于获益和问题解决的速度上,对于所付出的努力,即步数不敏感。在策略的变异上,研究发现其主要体现在其他策略运用的减少上。这说明被试组问题解决过程中,逐渐变得更为理性,不再采用次优策略,转而探索最佳策略。

对惯例的验证和描述研究借鉴并完善了前人的指标：(1)可靠性的增加。这代表了问题解决质量的提高。首先,为方便理解,本研究改变以往用四分位差作为衡量指标的做法(Cohen &Bacdayan,1994),直接用玩家完成每局游戏所用步数和被试组每局游戏得分作为衡量指标。通过这两个指标的刻画发现,被试组在重复解决问题的过程中,其可靠性逐渐增加,说明了惯例存在的可能。这是因为惯例的作用之一是节省认知资源,它的出现会使行为越来越自动化,进而空出更多的认知资源进行高水平的思考和更加复杂的决策(Becker,2008)。(2)速度的提高。它是问题解决效率提高的时间指标。本研究对其进行了两处修正：第一,研究用被试完成每局游戏的总时间(由电脑自动记录)代替以往研究(Cohen &Bacdayan,1994)采用各组完成每局游戏所用的平均时间(需事后计算)。这样,通过采用原始数据不仅增加了研究的生态效度,还使数据处理简洁化。第二,研究增加了平均步时这一指标。不同局甚至同一局游戏都可以用不同的步数来完成,每一步换牌时间直接体现了个体的思考时间,惯例的存在会使思考解决方案的时间缩短(Betsch,Fiedler,&Brinkmann,1998;Betsch,Haberstroh,&Höhle,2002)。分别以上述两个指标为因变量,以局数为自变量的回归分析结果均表明,随着局数的增加,被试组完成每局游戏,及每步换牌所用时间均随着局数的增加而减少,即问题解决的效率在提高。(3)重复行动序列的存在。这一指标以往只限于描述且仅列举了 UU*T策略(Cohen &Bacdayan,1994),本研究不仅总结了被试组在重新设计的TTT扑克牌游戏中其他的模糊行为模式;还总结了完整的行动序列。研究表明(表2),通过重复地解决同一类问题,被试组形成了惯例,其集中表现在换右上位置的牌(C)和明牌(U)上。由事后访谈可知,明牌是被试在惯例形成中为与对方进行配合而有意采用的方法。但换右上位置的牌则可能源于游戏中因不断进行推理和逻辑分析而更多应用大脑左半球的无意识行为,这可由随着被试意识性的增加其应用次数显著减少来证明(图7)。(4)偶尔的次优性。以往研究(Cohen &Bacdayan,1994)对此或进行进行简单陈述,或直接不分析(王建安,张钢,2008),本研究通过个案剖析形象说明了惯例的顽固性。(5)基于特定策略的反应模式。与之前预期相一致,本研究发现,被试组在完成任务过程中主要采用了两种最佳策略,这说明惯例不仅表现在行为层面,更表现在认知层面。

4.2 问题解决中的惯例的形成：微观发生视角下的表征重述

本研究表明,被试组通过在不到1小时的时间内重复地解决同一类问题,形成了提高问题解决效率的策略,即惯例。这一过程既没有反馈,也没有指导,惯例是如何形成的？显然,答案只能从重复性问题解决过程本身寻找。研究通过微观发生法的分析表明,惯例的形成表现为策略及行为的不断变化和调整,即认知表征由无意识走向意识,由程序性转向陈述性知识。这一过程符合表征重述理论的假设(Kamiloff-Smith,2001),可突出表现为两个阶段：

第一,行为掌握阶段,它包括表征水平I。由表4可知,阶段Ⅰ中被试组每局得分、步数、每局用时、每步用时均与余3个阶段差异显著,但3个阶段之间差异不显著。这符合Kamiloff-Smith(2001)关于表征水平 I是成功取向的假设,被试通过调整行为和策略以提高问题解决效率。通过表5及表6的分析可知,这一过程行为的掌握是突变的,因为本阶段的各项指标及所采用策略只与相邻的阶段Ⅱ差异显著,与其他阶段的差异均不显著。然而,本阶段被试问题解决效率的提高并不意味着惯例的形成。例如,虽然阶段I时有16组被试固定了策略,但后续阶段他们并未坚持这些策略,而是不断对其进行调整(表7)。

第二,表征重述阶段,包括表征水平 E1、E2和E3。在阶段I的基础上,被试进一步调整和优化自己的行为和策略,使其通达意识。这体现为三阶段内各项指标为代表的问题解决效率的缓慢提高(表4),其他策略使用频率的持续下降(图6)及无意识行为(换右上位置牌)的逐渐较少(图7)。与Kamiloff-Smith(2001)通过儿童实验对三类外显表征水平的清晰描述不同,TTT扑克牌游戏由于阶段Ⅱ和阶段Ⅲ被试的意识性无法测量,三类表征只能通过表7所示的各组被试策略使用的变化进行推测。表征水平 E1体现为阶段Ⅱ中被试策略的使用更为多变和灵活。例如,阶段I中偏向4♣2♣2♥策略的7组被试在阶段Ⅱ中有4组两种策略并存,而并存体现了表征之间的相互作用。再如,其他策略的使用率从11%下降为4%(图6)。表征水平E2体现为阶段Ⅲ中策略的使用更为丰富、连贯。例如,阶段Ⅱ中两种最优策略并存的 3组被试在阶段Ⅲ时均固定或偏向4♣4♥2♥策略,且其他策略的使用率进一步下降为3%。表征水平E3体现为阶段Ⅳ中策略使用的确定性。例如,阶段Ⅲ时有12组被试固定了策略,阶段Ⅳ有17组被试固定了策略。而且,与前3阶段两最优策略同时增加的趋势不同,阶段Ⅳ中4♣2♣2♥策略增加,但 4♣4♥2♥策略减少。这说明被试对两种最优策略有意识地进行了选择。

4.3 惯例的稳定性、意识性及与陈述性知识的关系

本研究采用微观发生法的设计和分析思路,阐明了惯例从无到有的产生过程,为其意识性、稳定性争议及其与陈述性知识关系提供了动态解释。由上述分析可推测：阶段I中被试致力于行为的掌握,形成的是程序性知识,惯例在这个过程中是无意识的,也未完全形成;直到阶段Ⅳ被试组才形成了问题解决的最优策略,并能用言语报告,即惯例已转变为陈述性知识。可见,惯例经历了由陈述性知识变为程序性知识,由无意识转向意识过程。这说明以往 Cohen和 Bacdayan(1994)所述的惯例是作为程序性知识进行存储的观点并不全面,惯例应是程序性知识与陈述性知识的结合。另外,从微观产生过程来看,惯例是不断变化(表7)的,会存在策略的调整、并存、偏向和固定几种状态。

上述解释与惯例生成观的描述不谋而合,本研究为其提供了实验支持。Feldman和 Pentland(Feldman &Pentland 2003;Pentland &Feldman,2005;Pentland et al.,2012)认为,惯例包含形式面和执行面两部分。前者说明惯例由什么组成和用来做什么,具有原则性;后者涉及组织惯例的具体化,指特定人在特定时间和地点参与特定组织惯例活动的真实行为。在任何实际的情境中,惯例的两个方面均由各种载体承载或驱动。在 TTT扑克牌游戏为载体的惯例中,作为抽象面,形式面不仅如前人所述(Becker,2008)存储于程序性记忆中,本研究证实,它也存储于陈述性记忆中。从惯例的微观产生过程来看,行为的掌握相当于惯例的执行面,而惯例形成的最终阶段则相当于形成了惯例的形式面。这一过程与以往研究者所述一致(Feldman &Pentland,2003;Pentland &Feldman,2005),体现了变化性与稳定性的统一：形式面作为目标在还没有达到或未达到理想状态时,会一直保持稳定;这时,执行面为了与其保持一致会不断变化。综合上述分析,当以微观发生的视角重新审视惯例时,惯例的生成观可重新表述为图8。

图8 惯例的新生成观图示

由图可知,惯例由相互联系和彼此转化的形式面和执行面组成,并由一定载体承载,其形成体现为由执行面通过表征水平I至E3的重述而通达形式面,并经历由程序性向陈述性知识以及由无意识向意识的转化过程。这从惯例产生过程的角度细化了生成观的表述。

Becker,M.C.(2007).Routines-Abrief history of the concept.In S.Ioannides,&K.Nielsen(Eds.),

Economics and social sciences: Boundaries, interaction and integration

.Cheltenham,UK:Edward Elgar Publishing.Becker,M.C.(2008).

Handbook of organizational routines

.Cheltenham,UK:Edward Elgar Publishing.Betsch,T.,Fiedler,K.,&Brinkmann,J.(1998).Behavioral routines in decision making:the effects of novelty in task presentation and time pressure on routine maintenance and deviation.

European Journal of Social Psychology,28

(6),861-878.Betsch,T.,Haberstroh,S.,&Höhle,C.(2002).Explaining routinized decision making:Areview of theories and models.

Theory and Psychology,12

(4),453-488.Bonini,N.,&Egidi,M.(1999).

Cognitive traps in individual and organizational behavior:Some empirical evidence

.CEEL Working Papers 1999-04,Computable and Experimental Economics Laboratory,Department of Economics,University of Trento,Italia.Cohen,M.D.(1991).Individual learning and organizational routine:Emerging connections.

Organization Science,2

(1),135-139.Cohen,M.D.,&Bacdayan,P.(1994).Organizational routines are stored as procedural memory:Evidence from a laboratory study.

Organization Science,5

(4),554-568.De Boer,E.A.,&Zandberg,T.(2012).Decision-making by organizational routines:The influence of agency and personality traits on deviating from formal organizational routines.

Journal of Quality Assurance in Hospitality &Tourism,13

(4),316-325.Egidi,M.(1996).Routines,hierarchies of problems,procedural behaviour:Some evidence from experiments.In K.Arrow,E.Colombatto,M.Perlman,&C.Schmidt(Eds.),

The rational foundations of economic behaviour

(pp.303-333).London:Macmillan.Feldman,M.S.(2000).Organizational routines as a source of continuous change.

Organization Science,11

(6),611-629.Feldman,M.S.,&Pentland,B.T.(2003).Reconceptualizing organizational routines as a source of flexibility and change.

Administrative Science Quarterly,48

(1),94-118.Kamiloff-Smith, A.(2001).

Beyond modularity: Adevelopmental perspective on cognitive science

(X.C.Miu Trans.).Shanghai:East China Normal University.[A·卡米洛夫-史密斯.(2001).

超越模块性——认知科学的发展观

(缪小春译).上海:华东师范大学出版社.]Kuhn D.,Goh W.,Iordanou K.,&Shaenfield D.(2008).Arguing on the computer:Amicrogenetic study of developing argument skills in a computer-supported environment.

Child Development,79

(5),1310-1328.Labatut,J.,Aggeri,F.,&Girard,N.(2012).Discipline and change:How technologies and organizational routines interact in new practice creation.

Organization Studies,33

(1),39-69.Luchins,A.S.(1942).Mechanization in problem solving:The effect of Einstellung.

Psychological Monographs,54

(6),1-95.Luwel,K.,Siegler,R.S.,&Verschaffel,L.(2008).Amicrogenetic study of insightful problem solving.

Journal of Experimental Child Psychology,99

(3),210-232.March,J.G.,&Simon,H.A.(1958).

Organizations

.New York:John Wiley.Nelson,R.R.,&Winter,S.G.(1982).

An evolutionary theory of economic change

.Cambridge,MA:Harvard University Press.Pentland,B,T.,&Feldman,M.S.(2005).Organizational routines as a unit of analysis.

Industrial and Corporate Change,14

(5),793-815.Pentland,B.T.,Feldman,M.S.,Becker,M.,&Liu,P.(2012).Dynamics of organizational routines:Agenerative model.