灰色关联度在股票综合评价中的应用

蔺小林, 陈壮民

(1.陕西科技大学 理学院， 陕西 西安 710021; 2.陕西科技大学 电气与信息工程学院， 陕西 西安 710021)

0 引言

有效的股票评价，可以给股票投资者在选择股票时提供一定的参考信息，能在一定的风险条件下提高投资收益，或在一定的投资收益水平上降低投资风险.

对于中长期股票投资者来说，要在保证资金相对安全的情况下实现增值，因此，有效的股票数据指标的综合评价就显得尤为重要.目前，对股票数据指标进行综合评价的常见方法有：(1)因子分析方法[1]，该方法通过对信息的降维和浓缩，把众多的影响因素归结为三个因子，并赋予这三个因子特定的含义，最终通过因子的得分实现对股票的评价.此方法的主要缺陷在于信息的降维和浓缩过程中，部分原有的有用信息丢失掉了，因此评价过程本身存在对原始信息的背离.(2)聚类分析方法[2]，通过多元统计分类方法对股票的价值指标进行分类，然后对因子进行打分，从而对股票的性能指标进行评价.该方法的不足有:一是需要大量的数据才能找出统计规律；二是假定样本服从某种特定的分布，且要求数据相互独立；三是数据本身灰度较大，不确定度较高.(3)ICA自适应算法[3]，该法通过修正步长，适用于时变性强的股票数据，但在进行独立成分分析时，把数据进行了分解，且认为分解后的数据间相互独立.

本文基于从上市公司发布的季度财务报表获取相关财务数据，结合灰色系统理论[4]、灰色关联度模型与算法[5-7]，利用灰色关联度权重的确定方法和客观多目标决策法[8-10]，对选取的十只股票进行综合评价分析.

1 灰色关联度多目标决策原理

考虑多指标决策方案集：A={方案1，方案2，…，方案n}={A1，A2，…，An}，多指标因素集：V={指标1，指标2，…，指标m}={V1，V2，…，Vm}，方案Ai对指标Vj的指标值记为Yij(i=1，…，n；j=1，…，m).一般情况下，指标分“效益型”指标和“成本型”指标.效益型指标是指属性值越大就越好的指标，如总资产利润率，每股收益，营业利润能力等；成本型指标是指属性值越小就越好的指标，如主营业务成本率，流动资金占用率等.

定义1(理想属性值)记理想方案A0对因素指标Vj的属性值为Y0j，且满足：

若Vj为效益型指标，则有

Y0j=max{Y1j,Y2j,…,Ynj}

若Vj为成本型指标，则有

Y0j=min{Y1j,Y2j,…,Ynj}

记方案集A对指标集V的决策矩阵为：

定义2(数据初值化处理) 若列向量的所有分量都表示效益型指标数据，则用第一个分量除所有分量(包括第一个分量)；若列向量的所有分量都表示成本型指标数据，则用第一个分量除以所有分量(包括第一个分量)，这样所得到新的列向量的方法称为列向量的数据初值化处理.

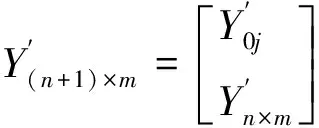
(i=1,…,n;j=1,2,…,m)

(1)

定义4(灰色关联度)记

灰色关联度rij定义为

(2)

其中ρ∈(0,1)，称为分辨系数，通常取ρ=0.5.

定义5(灰色关联判断矩阵 )由式(2)可以得到(n+1)×m个关联度系数rij，特别地，

r01=r02=…=r0m=1.由(n+1)×m个灰色关联度rij(i=0,1,…,n;j=1,2,…,m)构成灰色关联判断矩阵R(n+1)×m=(rij)(n+1)×m，即：

(3)

定义6(指标权重) 设(r1j，r2j，…，rnj)是所有n个方案对第j个指标因素的灰色关联度，rij(i=1,2，…，n)反映的是第i个方案对第j个实际指标因素值与理想值之间的关联程度，故平均值为：

(4)

反映了第j个指标因素在整个因素指标集V中所占的比重.

(5)

称ωj(j=1,2，…，m)为第j个因素指标的指标权重，W=(ω1，ω2，…，ωm)为m个因素指标的权重向量.

定义7(综合评价值)第i个综合评价值定义为

(6)

显然，Di值的大小表明实际方案Ai与理想方案A0的接近程度，因此，可以通过Di值对个案进行科学的评价分析.

2 应用灰色关联法进行多目标决策的步骤

对方案集为A={A1，A2，…，Am}，指标集为V={V1，V2，…，Vm}的实际问题，应用灰色关联法进行多目标决策的步骤为：

Step 1 根据原始方案集A和因素指标集V，确定理想方案A0和理想属性值Y0j，并写出决策矩阵Y.

Step 2 根据式(1)，对矩阵Y进行初值化处理，得初值化矩阵Y′.

Step 3 根据式(2)，计算出灰色关联度rij.

Step 4 根据式(3)，构造灰色关联判断矩阵R.

Step 5 根据式(4)和式(5)，计算出指标权重向量W.

Step 6 根据式(6)，计算出综合评价值Di，并比较其大小，进而确定方案的优劣.

3 个股的综合评价研究

为了评价股票时具有说服力和可比较性，本文选取了都属于地产板块的十只股票，且每个股票都是投资者追捧和关注的对象.选取的评价指标，也是投资者最为看重的七项财务数据指标，它们分别为：总资产利润率(%)、主营业务利用率(%)、成本费用利用率(%)、营业利润能力(%)、主营业务成本率(%)、净资产收益率(%)、每股收益_调整后(元).所选取的十只股票的七项指标的统计结果见表1.

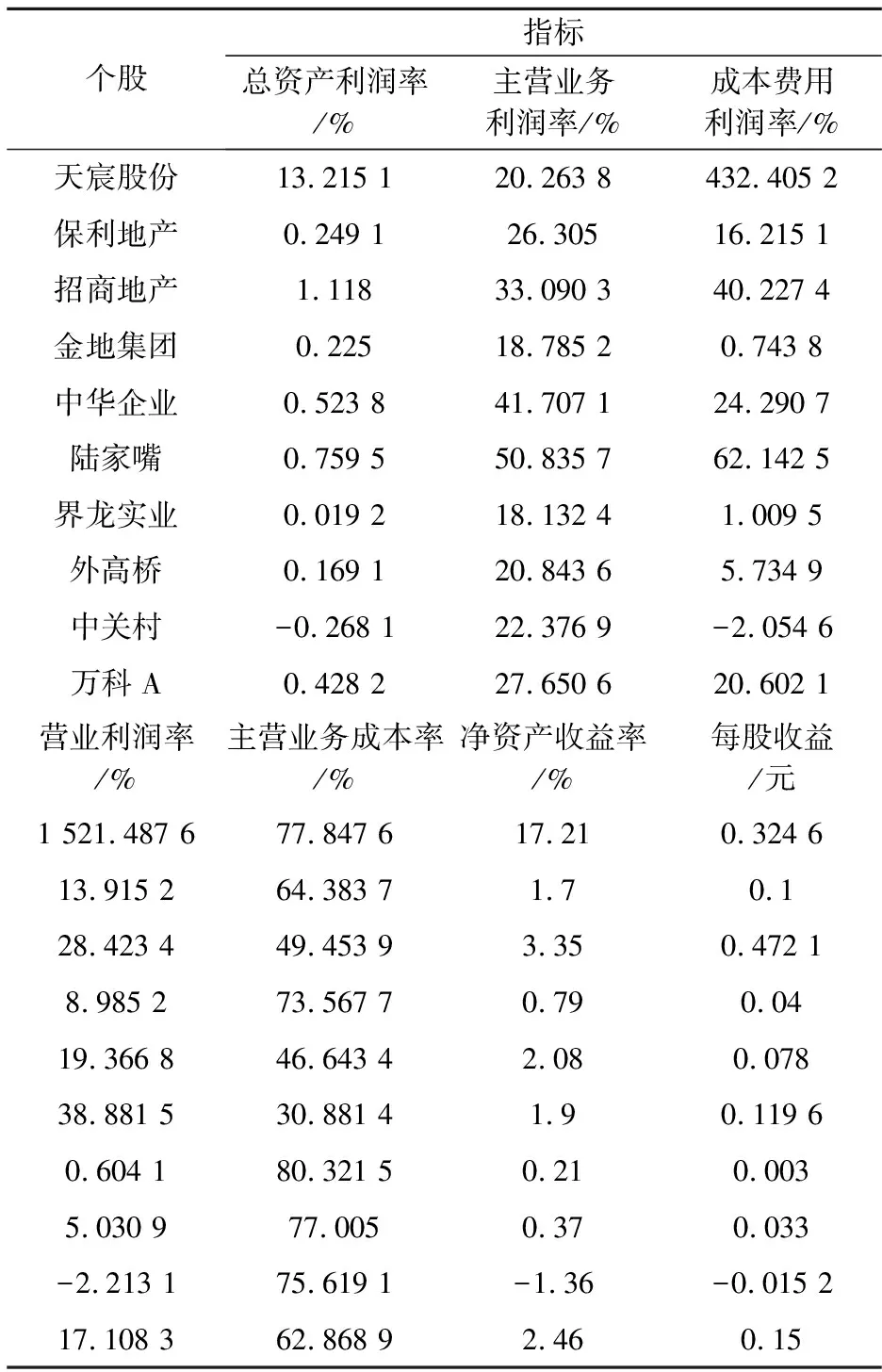
表1 十只股票七项财务数据指标

数据来源：爱股网，季度报告2013-03-31.

由表1可知方案集A={天宸股份、保利地产、招商地产、金地集团、中华企业、陆家嘴、界龙实业、外高桥、中关村、万科A}，指标集V={总资产利润率、主营业务利润率、成本费用利用率、营业利润率、主营业务成本率、净资产收益率、每股收益}.指标集V中，除了主营业务成本率属于成本型指标外，其他六个指标都属于效益型指标.

3.1 决策矩阵Y确定

根据表1所给数据，可得相对理想方案A0为：

A0={13.215 1 50.835 7 432.405 2 1 521.487 6

30.881 4 17.21 0.472 1}

于是可得到方案集A对指标集V的属性矩阵Y：

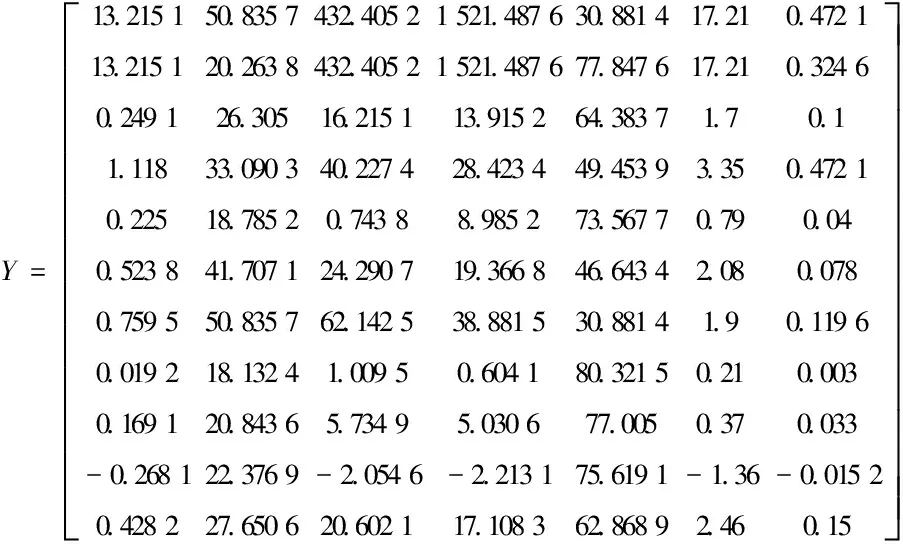
3.2 初值化矩阵确定

根据式(1)对矩阵Y进行初值化处理，得到矩阵Y′：

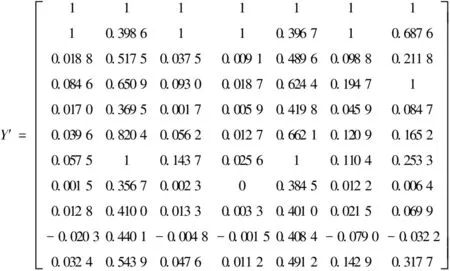
3.3 灰色关联度确定

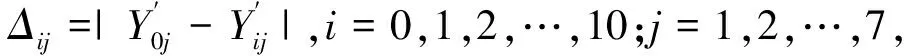
3.4 灰色关联判断矩阵确定

3.5 指标权重向量确定

由式(4)得关联度平均值：

0.578 6,0.424 9,0.417 4,0.560 0,0.432 3,

0.472 6)

由式(5)可得指标权重向量：

W=(ω1,ω2,ω3,ω4,ω5,ω6,ω7)=(0,127 4,

0.175 0,0.128 5,0.126 2,0.169 3,0.130 7,

0.142 9)

3.6 综合评价结果

由式(6)可得综合评价值：

D=(D1,D2,D3,D4,D5,D6,D7,D8,D9,D10)

=(0.748 0,0.223 3,0.413 1,0.157 0,0.308 9,0.424 0,0.130 6,0.156 2,0.127 9,0.254 1)

由此可知，

D1>D6>D3>D5>D10>D2>D4>D8>D7>D9

这十只股票的综合价值评价排序由高到低为:天宸股份、陆家嘴、招商地产、中华企业、万科A、保利地产、金地集团、外高桥、界龙实业、中关村.

本文所采用的数据来源于上市公司2013年3月31日发布的财务报表.我们所选取的十只股票在后来两个月的表现如何,表2给出了这十只股票从2013年4月1日开盘到2013年5月31日收盘两个月交易日实际涨跌幅的排序情况.

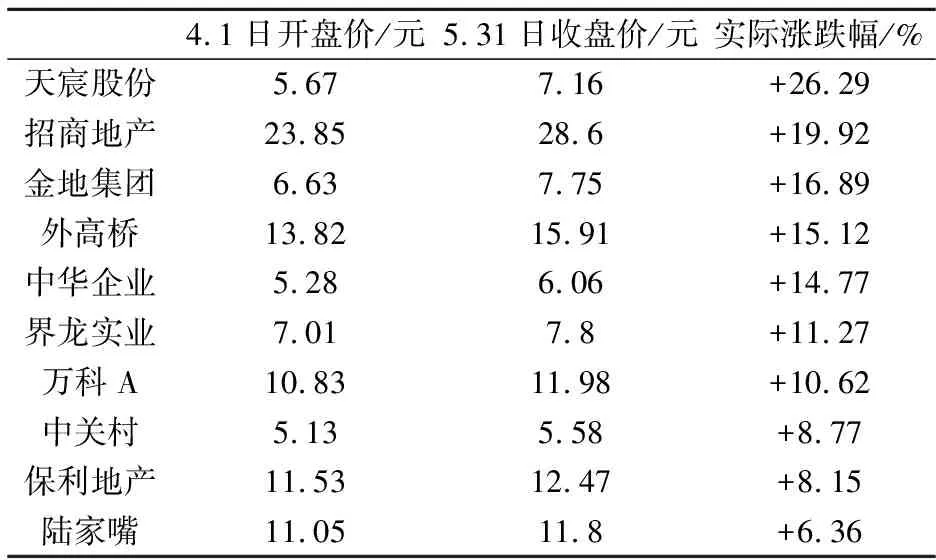
表2 十只股票在两个月内的实际涨跌幅

数据来源：雅虎财经网站.

从表2可知，这十只股票在两个月内的实际涨跌幅排序与综合评价值相比，排序完全正确的是天宸股份，排序相差一位的是招商地产和中华企业，相差两位的是万科A和中关村，相差最大的是陆家嘴，它在综合评价值中排第二，实际情况中却排在最后.在综合评价排序中，前五位中有三只股票仍然排在前五位，后五位中同样有三只股票仍然排在后五位.

针对股票对时变性和随机性都具有极强震荡的性质，对所选取的十只股票进行评价，从评价结果与实际情况比较来看，可以认为评价准确的股票有三只(天宸股份、招商地产、金地集团)，其准确率和可靠性已经很高.并且，评价准确的三只股票中，有两只(天宸股份、招商地产)按评价值是推荐选择的股票，且这两只股票的实际涨幅在选择的十只股票中排第一和第二位，这也较能说明应用灰色关联度方法对股票进行综合评价，其结果对股票投资者在选择股票进行投资时具有一定的参考价值.

当然，由于在验证股票实际情况时所选择的时间阶段的不同，国家在各个时间阶段出台的对股市有影响力的政策不同，整个社会的经济发展形势以及上市公司本身所实施的举措在各个时间阶段而不同，股票的真实情况和综合评价值吻合度也会有所不同.也正因为如此，投资者更要根据上市公司不同时间段的财务报告进行股票综合评价，通过横向纵向比较，适时调整投资策略.

4 结束语

通过对股票的综合评价研究，可以帮助投资者尤其是中长期投资者更加全面地了解和评价股票，散户可以避免盲目跟风而被套.投资者可以根据公司的季度或者年度财务报告，通过横向纵向对比股票综合评价值，提高对于所投资股票的深层次认识，适时调整投资决策.

本文在选取指标时，没有考虑更多的影响因素，而只是主观的选择了认为最重要的七项财务数据指标进行分析研究.同时，从灰色关联度的原理及决策过程看，由于选取指标存在人为的差异，不同的指标选择会导致最终的评价值也不尽相同.如果能以更加科学、有效、全面、合理的方式选择指标，其评价结果势必更为科学且对投资者决策时更具有参考意义.

[1] 王学民.因子分析在股票评价中的应用[J].数理统计与管理,2004,23(3):6-10.

[2] 黄 丽.聚类分析方法在股票评价中的应用[J].商业会计,2011,32(25):65-67.

[3] 郭崇慧,贾宏峰.基于一维搜索的ICA自适应算法及其在股票分析中的应用[J].数理统计与管理,2012,31(3): 564-570.

[4] 邓聚龙.灰色系统理论教程[M].武汉:华中理工大学出版社,1990.

[5] 田 民,刘思峰,卜志坤.灰色关联度算法模型的研究综述[J].统计与决策,2008,24(1):24-27.

[6] 罗 党,刘思峰.灰色关联决策研究方法[J].中国管理科学,2005,13(1):101-106.

[7] 鲁 峰.黄金泉.基于灰色关联聚类的特征提取算法[J].系统工程理论与实践,2012,32(4):872-876.

[8] 周 斌.由灰色关联度确定权重的客观多目标决策法[J].昆明理工大学学报(理工版),2003,28(5):159-161.

[9] 吕 峰,崔晓辉.多目标决策灰色关联投影法及其应用[J].系统工程理论与实践,2002,22(1):103-107.

[10] 杨竹莘,张军涛.区域科技创新能力的灰色关联综合评价研究[J].数学的实践与认识,2007,37(9):17-22.