基于混合核函数PLS的氧化铝粉流量预测

胡 羽， 张 洁

(1.兰州理工大学 能源与动力工程学院，甘肃 兰州 730050； 2.兰州职业技术学院 机电工程系，甘肃 兰州 730070； 3.兰州理工大学 数字制造技术与应用省部共建教育部重点实验室， 甘肃 兰州 730050； 4.兰州理工大学 机电工程学院， 甘肃 兰州 730050)

0 引言

现代大型预焙槽铝电解生产中，氧化铝输送是非常重要的一个环节，直接影响着电解槽的正常生产.氧化铝输送系统作为现代大型铝电解生产的重要组成部分，对铝电解节能减排的作用越来越重要.

在氧化铝输送过程中,需要对铝电解中的氧化铝粉流量作为主要参数进行在线精确测量，而应用于氧化铝生产的在线分析仪表由于受到精度不高、价格昂贵、无法适应恶劣的现场环境等因素的制约，很难满足氧化铝粉流量的在线测量[1].通过工艺过程分析，氧化铝粉流量与风压、风流量、风管调节阀开度、物料因素、温度及溜槽内物料量间的动态平衡关系等因素存在较强的相关性和非线性，其中与氧化铝粉流量相关的诸如风压、风流量等现场数据可以通过先进的计算机监控系统进行全面的检测，这为通过辅助变量对氧化铝粉流量在线测量提供了有力条件，因此将软测量技术应用于氧化铝粉流量的在线预测有着十分重要的意义[2-4].

软测量技术主要包括辅助变量的选择、数据采集和处理、软测量建模方法和软测量模型在线校正.而软测量技术的核心是软测量建模方法，核函数方法作为一种较新的机器学习方法, 在模式识别、工业过程建模等领域获得了成功应用[5-7].

偏最小二乘(PLS)作为一种多元统计分析方法[8]，在工业过程建模、化工领域得到了广泛的应用.PLS是一种同时考虑了输入输出数据，并对输入输出数据进行正交分解的回归方法.但是PLS也是一种线性算法，在处理非线性输入和输出数据时效果较差.Rosipal[9]将PLS与核函数理论相结合，提出了核偏最小二乘(KPLS)法.KPLS 的思想是将输入数据通过核函数映射到高维特征空间，在特征空间再运用PLS算法, 这样特征空间的线性PLS 就对应原始空间的非线性关系[10,11]，通过核函数方法的引入提高了PLS方法的非线性问题处理能力.

本文针对氧化铝粉流量需在线精确测量、在线分析仪表成本较高和测量滞后的问题，提出了基于两种核函数混合核的PLS氧化铝粉流量预测模型.利用工业现场数据验证，基于MKPLS模型可以提高PLS的非线性问题处理能力，获得了良好的效果.

1 基于混合核函数PLS的预测方法

1.1 KPLS算法

核偏最小二乘法作为一种非线性建模方法，将核函数法与偏最小二乘法相结合，增强了偏最小二乘法处理非线性问题的能力.核偏最小二乘法的思想是将原始空间输入通过核函数映射到高维特征空间，在高维的特征空间再运用线性的偏最小二乘法算法.这样就将原始空间的非线性问题转化为高维特征空间的线性偏最小二乘.

设样本集为X={x1,x2,…,xl},其中,xi∈RN,l为样本总数，引入一个非线性映射Φ，对应的空间记为F，将原始空间的输入样本xi∈RN,i=1,…,l映射为高维特征空间的Φ(xi)∈RF，Φ(xi)为F中的样本， 引入核函数，令K=ΦΦT， KPLS算法可表示如下[12,13]：

(1)初始化向量u；

(2)t=ΦΦTY，t←t/‖t‖；

(3)c=YTt;

(4)u=Yc，u←u/‖u‖；

(5)满足收敛条件，转下一步，否则转步骤(2)；

(6)K=(I-ttT)K(I-ttT)，Y=Y-ttTY；

回归系数B可表示如下：

B=ΦTU(TTKU)-1TTY

(1)

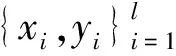
(2)

如果输出数据是一维向量，则

d=U(TTKU)-1TTY

(3)

KPLS预测的表达式可以表示为

(4)

1.2 核函数

核函数方法是对非线性数据处理的方法，对数据处理的方法中应用了核映射，采用非线性映射的方法将原始数据映射到特征空间，在特征空间中进行线性运算，在实际运用中增强了非线性数据处理能力.核函数从本质上而言实现了数据空间与特征空间之间的非线性变换，实现了向量的内积变换：

(xi,xj)→K(xi,xj)=Φ(xi)·Φ(xj)

(5)

而在进行向量内积变换时，核函数必须满足Mercer条件的任意对称函数.

常用的简单核函数有:

(1)高斯径向基核函数:

(6)

(2)多项式核函数:

K(xi,xj)=((xiTxj)+c)d

(7)

(3)指数型核函数:

(8)

(4)感知器核函数:

K(xi,xj)=tanh[ν(xi·xj)+c]

(9)

混合核函数方法是将两个或两个以上的简单核函数结合起来, 使得混合后的核函数具有更好的特性, 混合核函数依旧满足Mercer条件.

在常用的简单核函数中，高斯径向基核函数是局部核函数，学习能力强，泛化性能弱，多项式核函数是全局核函数，泛化性能强，学习能力弱.考虑到这两类核函数的优点与不足之处，将这两种核函数相结合构成混合核函数：

K(xi,xj)=β((xiTxj)+c)d+

(10)

β∈[0,1],β为可调参数，调节两种核函数对总的混合核函数权重.当β= 0时, 混合核函数变成为高斯径向基核函数;β=1时,混合核函数变成为多项式核函数.

2 混合核函数PLS在氧化铝粉流量预测中的应用

2.1 工艺分析

超浓相输送技术作为先进技术被国内各大电解铝厂广泛采用，该技术是利用低压风的能量作用，在风动溜槽中，让低压风通过透气板使氧化铝粉内冲入一定量气体，使氧化铝粉具有半沸腾状态，此时物料像水一样具有良好的流动性，靠首端压强及重力压差，产生水平分力，流态化的物料向前流动，完成输送任务.其特点是物料在风动溜槽呈流态化向前运动、固气比高、运动速度低、物料不易破碎、系统全密闭、所需风压低、风量小、自动化程度高[14-16].

在氧化铝输送过程中，需要对铝电解中氧化铝粉流量进行在线精确测量,若采用在线分析仪表，设备投资较大，维护成本高，并因较大的测量滞后而使得调节品质下降.

通过对氧化铝粉输送工艺流程和氧化铝粉流量的影响因素深入分析，结合实际生产过程中计算机监控系统检测的现场数据，选取了供料离心风机风流量、供料离心风机风压作为软测量建模的辅助变量.氧化铝粉流量预测值与辅助变量间的关系可描述为：

yt=f(Q(t),P(t))

(11)

2.2 混合核函数PLS的氧化铝粉流量软测量模型的建立

这里采用工业现场采集相关辅助变量的生产数据对预测模型进行验证，经过误差处理共获得有效数据257 组，从中任意抽取207组数据作为学习样本用于建模，剩余50组作为测试样本用于模型性能测试.

将单一核函数和混合核函数分别引入预测模型中，分别构建基于KPLS、MKPLS两种算法的模型并进行仿真，所采用的核函数形式如下：

MKPLS

K(xi,xj)=β((xiTxj+c)d+

β∈[0,1](β为可调参数，可以调解两种不同性能核函数在混合核中的比重).

为了验证预测模型的预测性能，这里对KPLS、MKPLS模型进行了仿真，仿真结果如图1、图2所示.

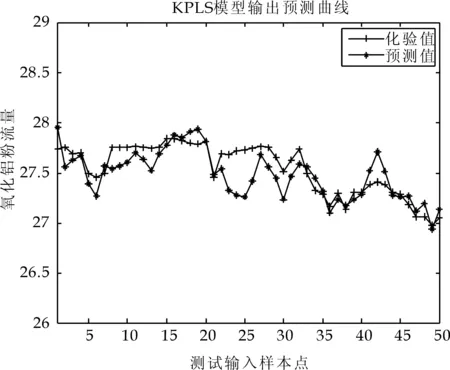
图1 KPLS模型预测曲线

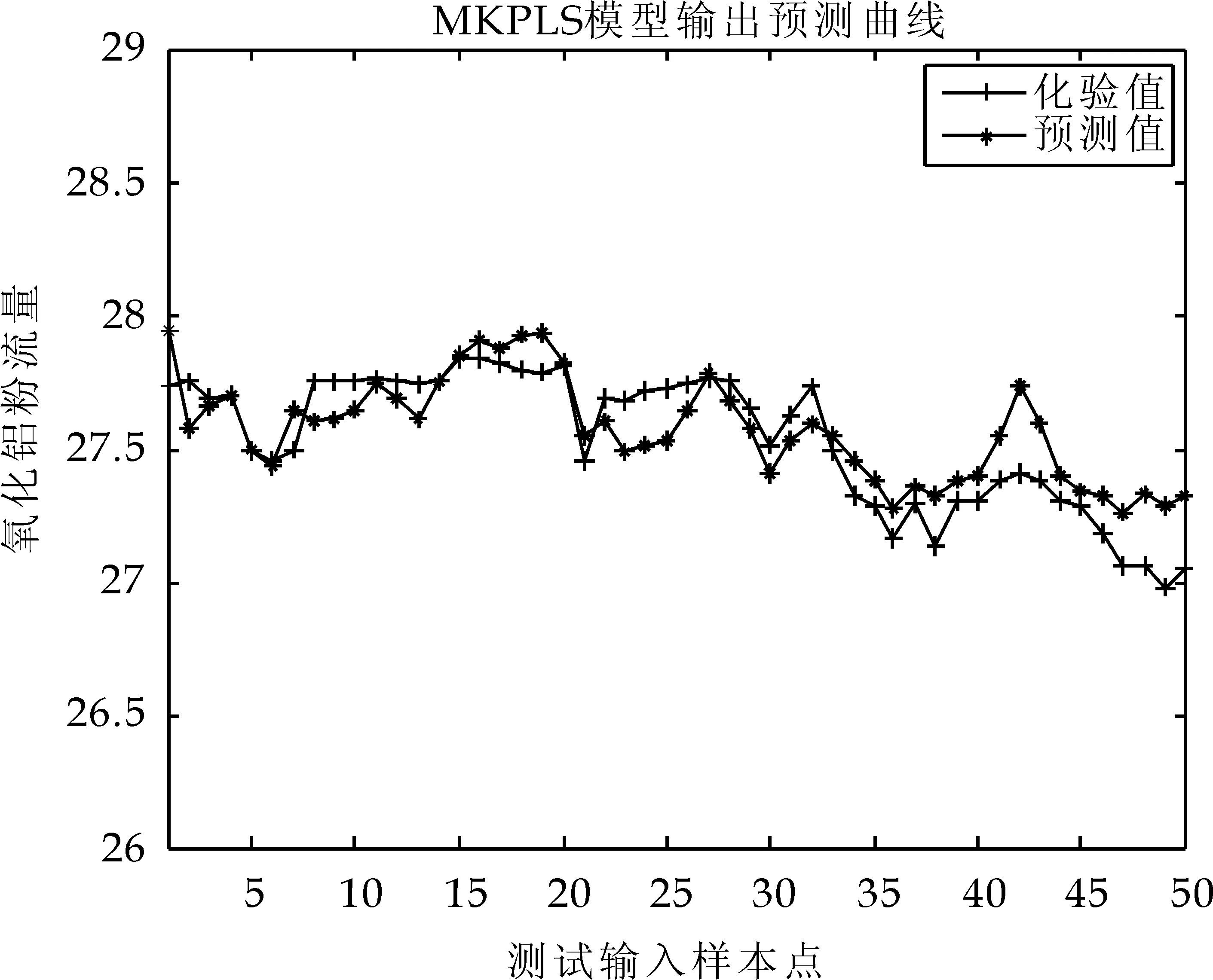
图2 MKPLS模型预测曲线

2.3 预测结果分析

采用测试样本对所得模型的泛化性能进行预测检验,为对模型性能做出评价，性能指标选为：各模型运行结果的最大绝对误差MAE、均方根误差RMSE两项指标，算式如下：

(12)

(13)

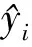
采用测试样本对模型性能进行测试，并计算前述性能指标，不同模型精度对照表如表1所示，不同模型预测误差曲线如图3、4所示.

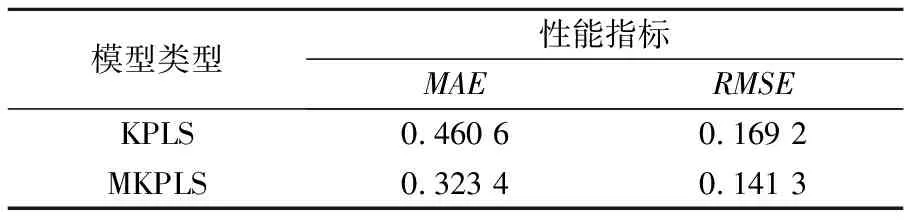
表1 不同模型的精度

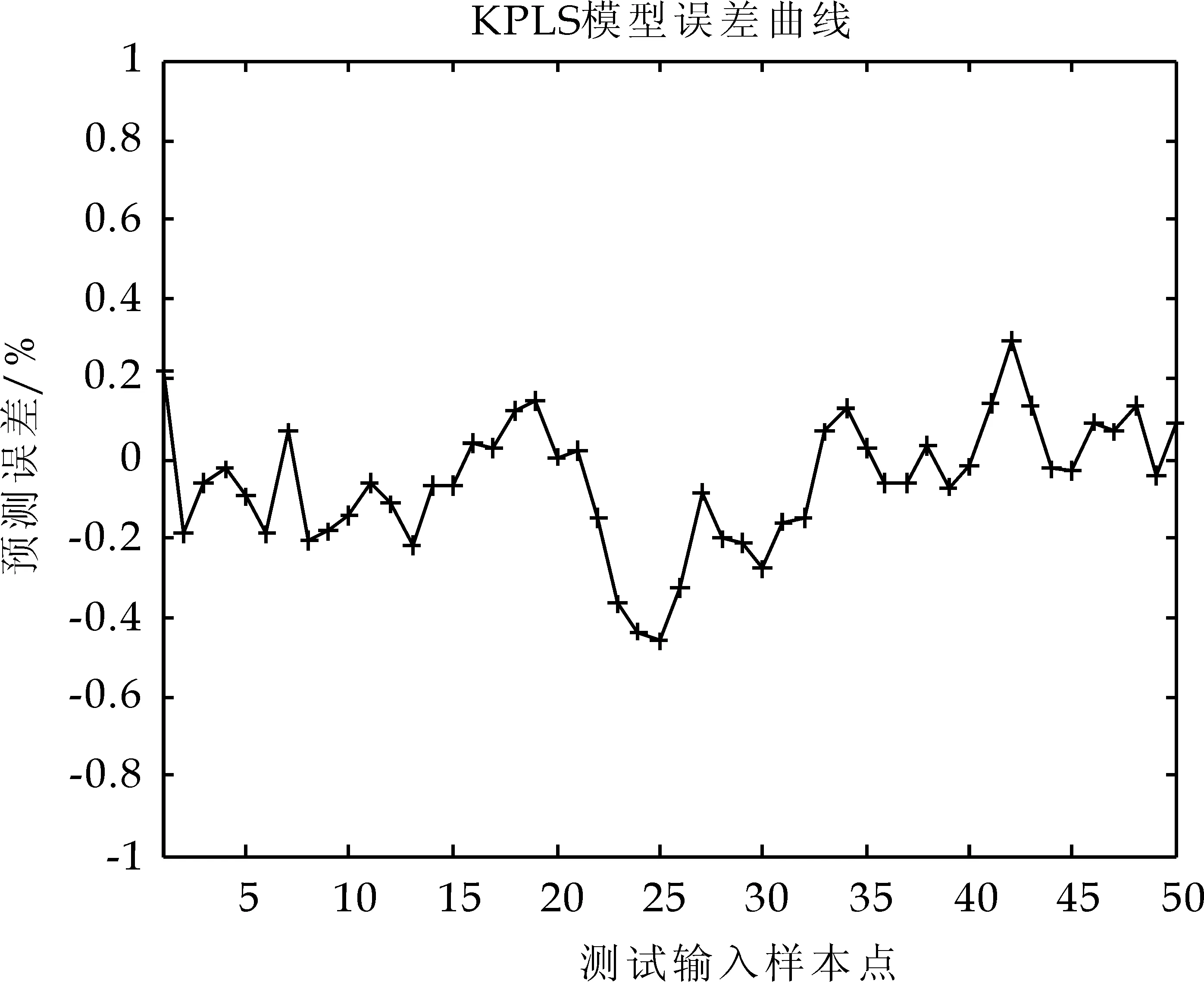
图3 KPLS模型预测误差曲线

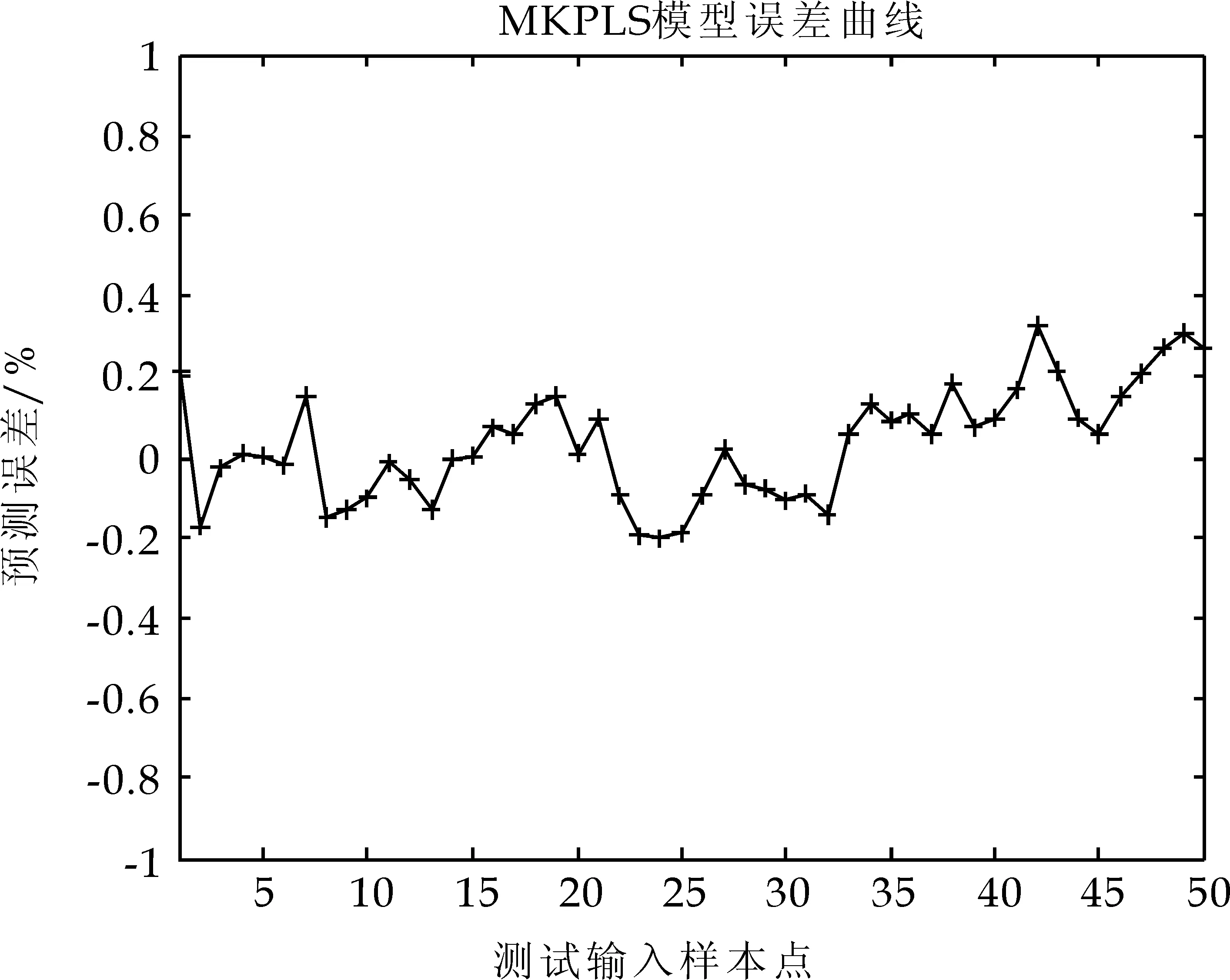
图4 MKPLS模型预测误差曲线

从表1、图3、图4可以看出：两种模型中，MKPLS泛化性能最优.由于采用MKPLS方法对数据进行了处理，提高了PLS方法的非线性问题处理能力.工业数据仿真结果表明，混合核函数相对于单一核函数来说，MKPLS氧化铝粉流量预测模型最大绝对误差为0.323 4，均方根误差为0.141 3，预测模型具有较高的预测精度以及能够较好的跟踪数据变化，说明本文所建立的混合核函数PLS的氧化铝粉流量软测量模型是有效的.

3 结束语

针对氧化铝输送过程中，需要对铝电解中氧化铝粉流量进行在线精确测量，本文提出了运用核偏最小二乘和核函数的方法，分别构建了基于单一核函数和混合核函数的氧化铝粉流量PLS预测模型，并采用工业现场数据进行验证，结果表明，与单一核函数的预测模型相比，混合核函数的氧化铝粉流量PLS预测模型具有较高的预测精度和良好的泛化性能等特点.

[1] 朱 波.氧化铝生产苛性比值软测量神经网络模型的在线修正方法研究[D].长沙：中南大学,2005.

[2] 俞金寿.软测量技术及其应用[J].自动化仪表,2008,29 (1)：1-7.

[3] Gonzalez G D. Soft sensors for processing plants[J].Proceeding of the Second International Conference on Intelligent Processing and Manufacturing of Materials.1999,1:59-69.

[4] 鲁春燕.氧化铝输送中氧化铝粉流量的软测量方法研究[D].兰州：兰州理工大学,2009.

[5] 俞金寿.工业过程先进控制技术[M].上海：华东理工大学出版社,2008:83.

[6] Müller K R, Mika S, Rätsch G,et al.An introduction to kernel-based learning algorithms[J].IEEE Transactions on Neural Networks,2001,12(2):181-202.

[7] 陶少辉,陈德钊,胡望明,等.基于核函数的非线性分类相关分析及其在化学模式识别中的应用[J].分析化学,2005，33(1):50-53.

[8] Word S,Sjöström M,Eriksson L.PLS-regression:a basic tool of chemometrics[J].Chemometrics and Intelligent Laboratory Systems,2001，58(2):109-130.

[9] Rosipal R,Trejo L J.Kernel partial least squares regression in reproducing kernel hilbert space[J].Journal of Machine Learning Research,2001,2(6):97-123.

[10] Kim K,Lee J M,Lee I B. A novel multivariate regression approach based on kernel partial least squares with or- thogonal signal correction[J].Chemometrics and Intelligent Laboratory Systems,2005,79(1-2):22-30.

[11] Jia R D,Mao Z Z,Chang Y Q,et al.Kernel partial robust mregression as a flexible robust nonlinear modeling technique[J].Chemometrics and Intelligent Laboratory Systems,2010,100(2):91-98.

[12] 王华忠,俞金寿.基于核函数主元分析的软测量建模方法及应用[J].华东理工大学学报,2004,30(5):567-570.

[13] 宋海鹰，桂卫华，阳春华，等.基于核偏最小二乘法的动态预测模型在铜转炉吹炼中的应用[J].中国有色金属学报，2007，17(7)：1 201-1 206.

[14] 杨晓军,梁 冶.电解铝厂氧化铝浓相输送技术应用实践与改进[J].轻金属,2004(8):28-30.

[15] 那生巴图.氧化铝超浓相输送系统的改进[J].内蒙古民族大学学报,2008,14(2):13-14.

[16] 朱振国,蒋 雷.铝电解超浓相输送技术的应用[J].山东煤炭科技,2009,6(1):48-50.