改进遗传算法求解静态车间调度问题

栾 飞, 傅卫平, 邓明明， 王 雯, 来春为

(1.陕西科技大学 机电工程学院， 陕西 西安 710021； 2.西安理工大学 机械与精密仪器工程学院， 陕西 西安 710048)

0 引言

车间调度(Job-Shop Scheduling Problem，简称JSP)主要是针对一项待加工任务，寻求在满足生产加工的各种约束条件下，通过安排工件使用哪些设备加工的先后顺序，进而达到制造总时间最短或总成本最低[1].在理论研究中，车间调度问题常被分为动态车间调度问题和静态车间调度问题.当安排完工件的加工顺序后，在下达执行过程中，没有任何突发事件发生，也就是加工前安排的顺序不需要做任何修改和变动，这种调度问题成为静态调度.相反，如果在加工过程中，有各种突发事件发生，进而要重新进行调度的问题称为动态调度.

目前解决车间调度的方法主要有：滚动窗口、规则仿真、多智能体和智能算法等[1-5].基于滚动窗口的方法主要是将整个调度问题分解为在各个子区间段的调度问题，通过寻求各子区间的最优调度结果，来达到寻求整个调度问题最优解的目的，其难点在于选择子区间的大小不好确定；基于规则的调度方法，首先设定好的规则库.加工开始后，根据相应规则决定下一步操作的方案.其优点是不必进行大量的计算，方便易行.缺点是灵活性差，难以适应不确定变化;基于多智能体的方法，通过把人工智能的Agent概念引入车间调度工作中，将车间生产的各个组成部分看作一个个具有独立思维能力、对外协作能力和通讯能力的Agent，多个Agent相互协商来完成车间调度;基于人工智能的优化算法，由于对于问题模型的要求不高，且能够利用某些机制跳出局部最优，得到全局最优解，使得其在求解生产调度等复杂优化问题中得到了广泛的应用，但当调度问题的规模达到一定程度时，其解的质量与计算速度就得不到保障[6].

传统遗传算法，在理论上可以搜索得到最优解，但在求解实际问题的过程中会产生大量的非法解，使得算法收敛速度大大降低，当种群数量达到一定规模后，解域随之增大，使得种群采样点对于解域的全局覆盖率就会降低，从而增大了算法“早熟”的概率.

因此，本文采用多色集合理论中的围道矩阵来建立遗传算法的约束模型，使得编码、解码和变异等遗传操作在围道布尔矩阵的范围内进行，使算法的搜索过程在有效的解域内进行.也就是说，改进后的遗传算法通过缩小解的搜索范围，来保证所得解的有效性，并提高了算法的收敛速度.

1 车间调度问题的数学模型[7]

在描述JSP问题时，假设M代表设备数量，N代表工件数量，P为工序数量，I为所有设备的集合.Ieg表示工件e的第g道工序的可选设备集合，Ieg⊆I；Je为工件e需要加工的工序数.X表示工件的加工顺序，Segk为工件e的第g道工序在设备k上的开始加工时间；Eegk为工件e的第g道工序在设备k上的完工时间；Tegk为工件e的第g道工序在设备k上的加工时间，且k∈Ieg，则有Eegk=Segk+Tegk；Ep为最后加工工序的完工时间；MS为所有工件的最后完工的时间.

当工件e的第g道工序和工件i的第j道工序在同一台设备上执行，同时工序j仅先于工序g加工时，Qijeg=1，否则Qijeg=0；若工件e的第g道工序在设备k上执行，则Xegk=1，否则Xegk=0.

若某调度问题共有S种加工顺序，要求总的流通时间最短的加工顺序，先求取每个加工顺序x(x∈{1,…,S})对应的工件流通时间.显然，顺序x中最后加工工序的完工时间即是所有工件的最后完工时间.

MS=Ep

(1)

目标函数F(x)为

F(x)=min(MSx)=min((Ep)x)

(2)

X=1,…,S

S.T.Segk-Ee(g-1)n≥0

e=1,…,N;g=1,…,Je;Xegk=1,Xe(g-1)n=1

(3)

Segk-Eigk≥0

e=1,…,N;g=1,…,Je;Xijk=1,Xegk=1,Qijeg=1

(4)

在本文的车间调度问题中，假设有5种不同类型的工件，工件的最大工序数为6，各工件的批量分别为5，4，3，2，1，则共有工件15件，且每道工序可以加工的设备有多台，加工设备共有6类.调度的目标是针对待加工任务寻找一个合理的加工顺序方案，使得总的加工流程时间最短.

2 基于多色集合的车间调度约束模型

2.1 多色集合理论简介

多色集合理论是一种新的系统理论和信息处理的数学工具.它的核心思想就是使用相同的数字模型仿真不同的对象(产品、设计过程、工艺过程和生产系统等)，描绘元素间的层次结构和复杂关系，在集合层和逻辑层组织和处理信息，在数量层解决底层数量大小问题[8-10].

围道，即是多色集合中的颜色，在应用中代表被仿真对象的性质、属性、特性等，是系统技术概念的抽象和概括.一般用多色集合和多色图对复杂生产系统或机械产品进行仿真时，常常用“围道”这一概念替换“颜色”这一术语[11].

2.2 基于多色集合的数学模型

本文以一个5×6的JSP调度问题为例，运用多色集合理论来描述工艺与机床之间的约束关系,如表1所示；进一步可以获得工序-机床围道布尔矩阵，如图1，图2，图3, 图4, 图5所示，通过该图可以清楚地看到同一类工件的工序及对应加工机床的实时状态.

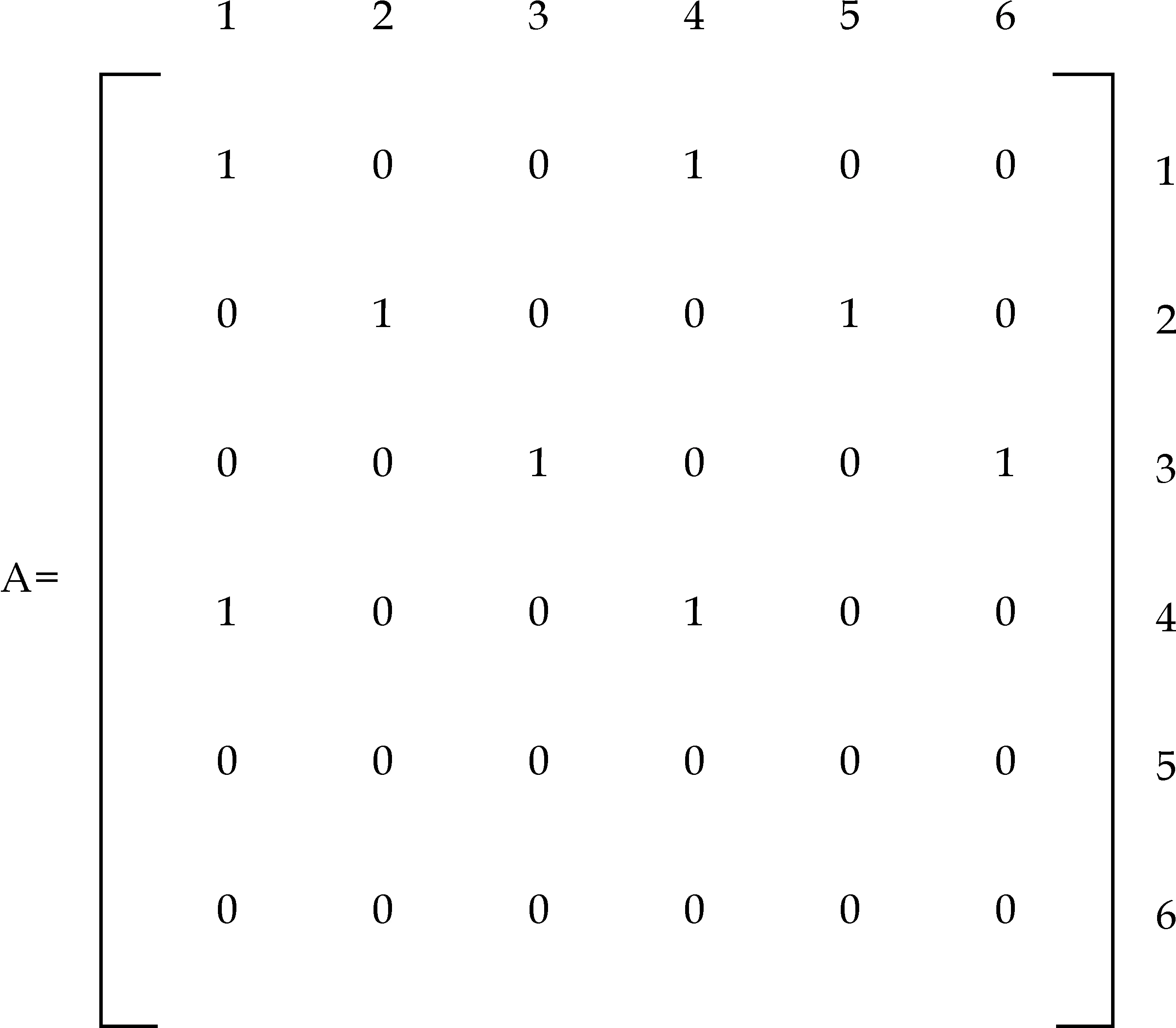
图1 工件1的工序—机床围道矩阵

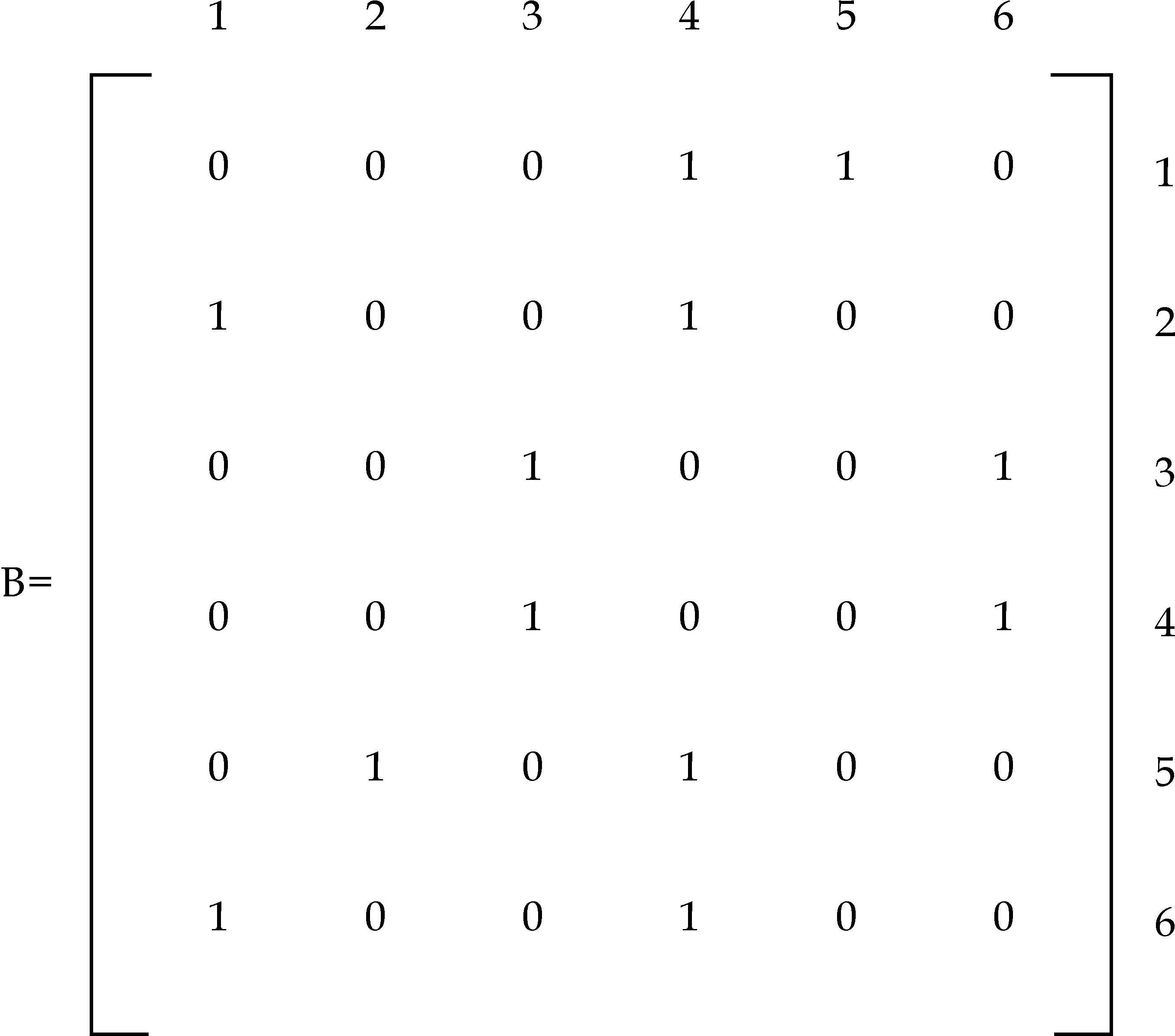
图2 工件2的工序—机床围道矩阵

图3 工件3的工序—机床围道矩阵

图4 工件4的工序—机床围道矩阵

图5 工件5的工序—机床围道矩阵

在各类工件对应的工序-机床围道矩阵中，行表示加工设备的编码；列表示对应工件工序编码；矩阵内数据为1，表示横坐标对应工序可以在纵坐标对应的机床上加工，0则相反.

2.3 车间调度的约束模型

本文通过建立工序—机床围道矩阵作为车间调度的约束模型,遗传算法的相应操作都在其范围内进行.通过约束模型中搜索相关信息，可以得到工序隐性编码序列如表2所示.求解时，通过搜索相应的工序—机床围道矩阵,找到工序的机床编码,再根据机床的实时状态选择相应机床编码进行染色体的显性编码.通过以上操作，使GA算法的所有操作都在围道矩阵内进行,大大缩小了搜索的范围,克服了传统遗传算法的各种不足.另一方面,通过采用单层隐性GA编码,使得算法的空间与时间复杂度得到了降低，也有效地提高了GA的搜索效率.

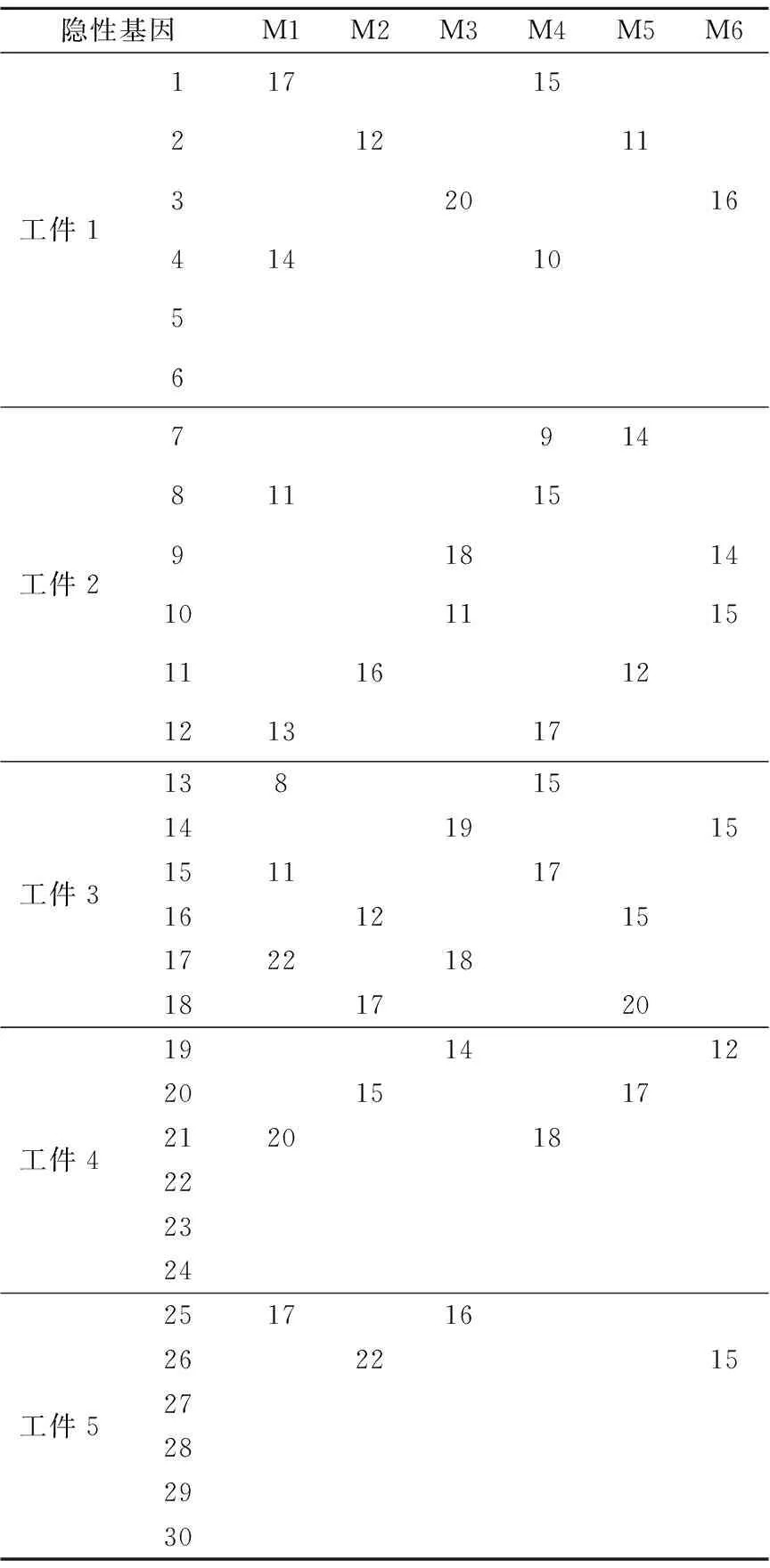
表2 工序隐性编码信息表

3 改进后的GA操作设计

3.1 改进GA的操作流程

遗传操作的内容包括：编码解码、适应度评价、选择、交叉和变异.就车间调度问题而言，其属于NP-hard问题，在求解过程中必须要考虑解的合法性和可行性，求解的目的不仅要寻找最佳的排序方案，还要选择最合适的加工设备.针对车间调度问题的这种特征，使得相应的遗传操作过程也较为复杂.图6为基于多色集合约束模型的遗传算法求解JSP问题流程图.

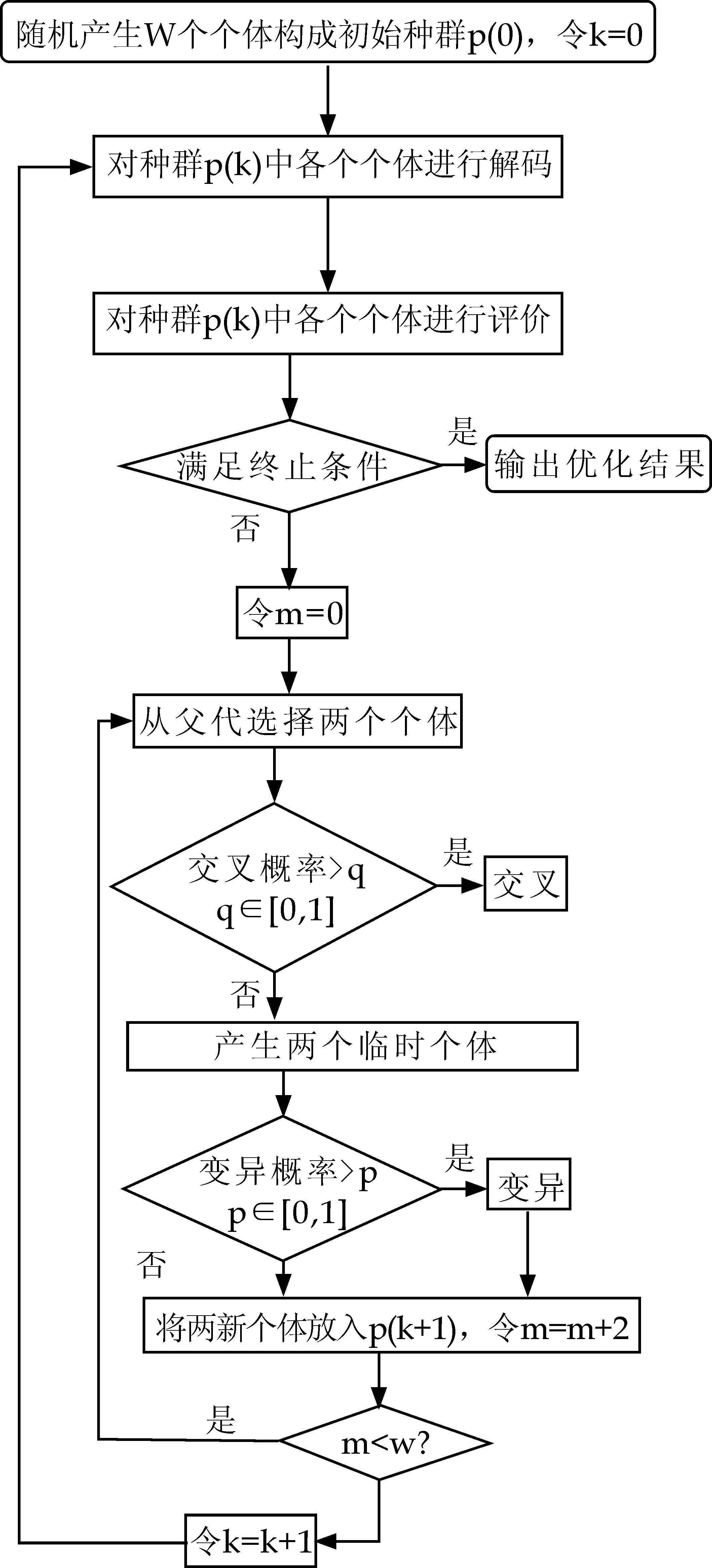
图6 基于约束模型的遗传算法流程图

3.2 改进GA的编码

车间调度问题的遗传编码必须考虑其合法性和可行性，具体可按以下步骤进行.

(1)以总工序数作为染色体的长度.例如，有A、B、C、D、E类工件数量为分别为5、4、3、2、1，则首先对工件加工次序进行随机排序，生成显性染色体如下.

BACDABCABACBEAD

其中：第一次出现的B表示B类工件的第一个，第二次出现的B表示B类工件的第二个，以此类推.

通过搜索相应的工序-机床围道布尔矩阵信息，产生对应隐性染色体，如下所示.

B11…B1mA11…A1mC11…C1m…DK1…DKm

其中：A11为A类产品的第一个工件的第一道工序，其余以此类推.

(2) 染色体的确定.本方案将工序的可用机床代码作为遗传操作的染色体，也就是染色体的信息可以直接从围道矩阵中获取，进而可以保证解的有效性，缩小搜索范围，提高收敛速度.

以上述5×6的多件调度问题为例，根据围道矩阵生成的染色体编码，如下所示.

213412312132514

根据染色体中的工件信息，搜索相应工件的工序-机床围道矩阵，找出可对其加工的机床信息，产生隐性染色体编码，如下所示.

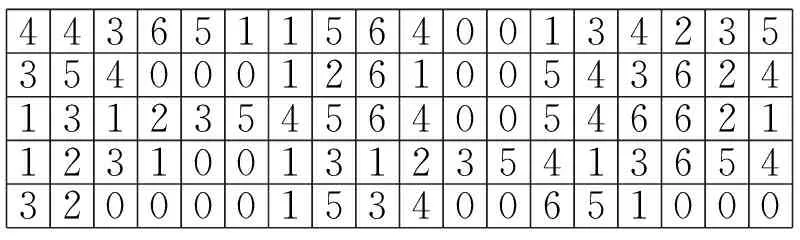
443651156400134235354000126100543624131235456400546621123100131235413654320000153400651000

1～6码位为第一个工件2的工序隐含位，完成这6道工序的加工机床为：4、4、3、6、5、1，以此类推，后面的各段连续6位码位分别表示对应工件的加工机床信息.

3.3 改进GA的解码

解码的目的在于按照工艺约束模型来计算每道工序的开始时间、完工时间.具体过程为：根据染色体编码，反向搜索各工件的工序-机床围道矩阵，从而获得各工序在相应机床上的加工时间，并在满足各工件内部工序约束的基础上，按照染色体(加工机床编码)对应的工序，来对毎台机床上安排的所有工序进行排序.例如，上例的5×6的单件调度问题所生成的一条染色体如下：

153400413654432235651000320000

根据染色体编码序列获取各个机床的加工信息如下：

机床1的可加工工序为：A的工序(1)、B的工序(2)、C的工序(3)、D的工序(3)、E的工序(3)，后续机床与此类似.

根据机床的可加工工序编写出染色体中的机床，找到对应的时间，计算相关参数如下：

每道工序的开始时间=max(机床的最早释放时间，上到工序的最早完成时间)

每道工序的完工时间=此工序的开始时间+工序的加工时间=完成此道工序的机床释放时间

此时，须注意在计算时间时，还得考虑不能超过机床的最大约束时间，这在生产排程中是要优先考虑的，因为目标函数是求总的加工流程时间的最小值.具体过程如下：

(1)将每台机床上各工件的第一道工序先进行排产，并返回工序-机床围道矩阵，获取其对应加工时间.

(2)按照工序约束与机床约束的双重约束，依次确定各机床上各任务的开始和完工时间.

(3)确定出每台机床上所有任务的开始和完工时间，即可获所有任务的排程方案，也就完成了解码过程.

对于多批量调度问题的解码方式，与上述的单件调度问题类似.

3.4 基于约束模型的适应度值计算[7]

在遗传算法中，以个体适应度的大小来确定该个体被遗传到下一代群体中的概率.个体的适应度越大，该个体被遗传到下一代的概率也越大.反之则越小.个体适应度具体计算过程如下.

设公式(1)对应函数值为fk，定义适应度函数fit(k)为fk的倒数，即

fit(k)=1/fk

(5)

式中：k-染色体标识.

可知公式(5)满足适应度函数要求，即

(1)由fk>0，可知fit(k)>0，则满足非负性要求.

(2)目标函数值fk减小时，适应度函数fit(k)的值增大，而调度优化的目标是求得目标函数值fk的极小值，所以目标函数的优化方向对应适应度增大的方向.

适应度值的计算过程如下.

步骤1 计算染色体中按解码后的顺序加工的各工序的开始时间和完工时间.

设工序i(i=1，…，n)的开始时间为Si,完工时间为Fi，在设备j上的加工时间为Pi，则Fi=Si+Pi，所以主要是计算Si.Si的计算过程如下：

(a)根据工序i的编号，搜索工序—机床围道布尔矩阵，确定它是所属工件的第几道工序.若i不是所属工件的第一道工序，则搜索工序—机床围道布尔矩阵，确定工序i所属工件的上一道工序的编号i0，再根据工序编号i0确定工序i所属工件的上一道工序的完工时间为PREFi，则要求Si≥PREFi；若i是所属工件的第一道工序，则要求Si≥0.

(b)根据工序i的编号，确定加工工序i在设备j上加工的上一道工序的编号.若工序i是设备j上的第一道工序，设备j开始加工的时间为MSj，则要求Si≥MSj；若工序i不是设备j上的第一道加工工序，设备j上加工的上一道工序的完工时间为PREMj，则要求Si≥PREMj.

步骤2 根据公式计算fk.

步骤3 根据公式计算适应度fit(k).

3.5 选择与交叉

在选择染色体时，按照适应度值的计算结果，将对应适应度值最好的染色体不经过后续环节，直接复制进入下一代种群，以此来保证优良基因的传播.

交叉是按一定的交叉概率P随机选择两个染色体，然后交换两个个体上对应的部分基因段，产生两个新个体，之后在解的空间中进行有效搜索，以确定哪些是适应度较高的个体，进而进行后续操作.对于交叉操作来，交叉算子的设计是其中的关键工作，一般要求既不要太多地破坏个体编码串中的优良模式，又要能够有效地产出一些较好的新个体.交叉算子的设计包括两个方面的内容：如何确定交叉点的位置；如何进行部分基因交换.交叉的具体操作过程如下所示(其中斜体部分为交叉的片段).

父代染色体为：

Chrom1

153400413654431235651000320000

Chrom2

423100446651164512321000120000

子代染色体为：

Chrom1′

153400446651164512321000120000

Chrom2′

153400413654431235651000320000

3.6 基于约束模型的变异

本文的变异过程也是在围道矩阵的约束下进行的.首先，根据经验确定变异概率Pi，再据此确定变异的基因码位i.然后，搜索工序-机床围道布尔矩阵，寻找对应码位的可替换机床编码，进而产生新个体.最后，计算新个体的目标函数Z′，并比较新旧染色体对应的Z与Z’，如果Z′较Z优秀，则变异，反之则不变异.

旧染色体为：

153400413654431235651000320000

需要变异的码位为：2、8、13、16

新染色体为：

123400443654631535651000320000

4 仿真实例

以上述5×6单件调度问题为例，在该例当中有五种产品分别为：A、B、C、D、E,每个工件最多有6道工序，可供选择的机床为6台.总工序数=工件数×max(各工件所包含的工序数)，结果为5×6=30道工序.

以调度任务开始执行时刻为零时刻，设各台设备相对该时刻的开始加工时间为0.运行参数如下：种群大小为50,交叉概率为0.6，变异概率为0.08，最大进化代数为100.用MTILAB语言编写仿真程序，其运行结果的遗传曲线如图7所示(其中，横坐标表示遗传算法的迭代次数；纵坐标表示遗传算法每一次迭代所得到的最小完工时间).

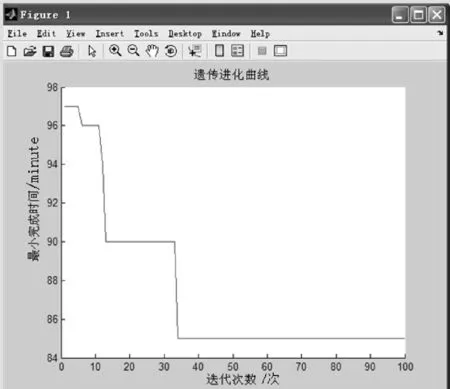
图7 实例仿真遗传进化曲线

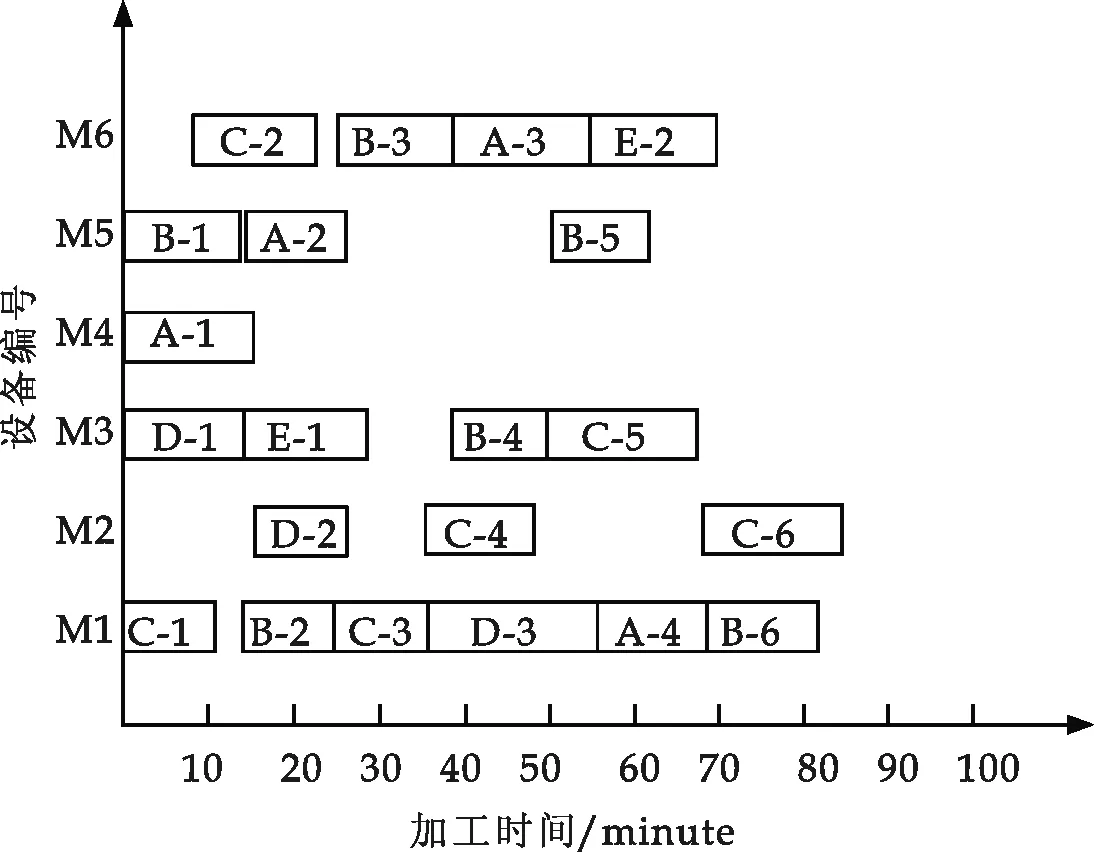
图8 实例仿真的调度结果甘特图

由图7的GA进化曲线可知，最优解为85 minute(最短加工时间).算法能够在40代时，从97较快地收敛到85，且得到的结果较稳定，对应的调度结果甘特图如图8所示(其中，横坐标表示加工时间；纵坐标表示对应的加工设备；矩形图表示工件在对应机床上的加工时间跨度).例如，C-1表示，工件C的第一道工序在M1上加工，起止时间为0～9 minute.

5 总结

由于车间调度问题属于复杂的NP-hard问题,受到了多种因素约束，运用传统遗传求解确实可以得到一些较优解，但是在求解过程难免会出现诸如“早熟”、“非法解”、“收敛过慢”等问题，使得其在实际车间作业调度领域的应用受到极大的限制.

针对这种不足，本文引入多色集合理论的围道矩阵来建立车间调度问题的多重约束模型，使得建模方式大大简化.另外，采用了单层遗传编码方法，使得遗传编码的空间和时间复杂度得到了降低，进而使搜索过程更加简单明了.因此，改进后的遗传

算法能有效地克服传统遗传算法的诸多缺点，使得遗传算法在车间调度领域的应用更加广泛.最后，还通过具体实例的仿真，验证了该算法的优势.

[1] 张娟云．基于MAS的车间动态调度三维仿真平台研究与开发[D]．西安：西安理工大学，2008．

[2] 王国新．基于仿真的调度规则组合决策研究[J]．北京理工大学学报， 2006，26(7)：598-601．

[3] Cao Yan，Zhao Ru-jia．Workshop scheduling based on a rule restrained colored petri net and the development of a scheduling system on the internet/intranet[J]．International Journal of Plant Engineering and Management，2004，9(3)：164-169．

[4] 郑旭栋．基于多智能体的车间调度系统研究[D]．上海：上海交通大学，2007．

[5] 郭东芬，李铁克.基于约束满足的车间调度算法综述[J]．计算机集成制造系统，2007，13(1)：117-125．

[6] Zhang G，Gao L，Li P．Improved genetic algorithm for the flexible Job-Shop scheduling problem[J]．Chinese Journal of Mechanical Engineering，2009，45(7) ：145-151．

[7] 葛凌志．多品种变批量零件柔性混流制枣运行系统的研究[J]．机械制造，2011，49(8)：49-51．

[8] Li Z，Xu L．Polychromatic sets and its application in simulating complex objects and systems[J]．Computers and Operations Research，2003，30(6)：851-860．

[9] Xu L，Li Z， Li S．A polychromatic sets approach to conceptual design of machine tools[J]．International Journal of Production Research，2005，34(12)：2 397-2 421．

[10] Xingqin G， Zongbin L， Zhao L．Study on modeling and reasoning technology of design based on chromatic sets[J]．China Mechanical Engineering，2006，17(3)：255-259．

[11] 李宗斌， 高新勤， 赵丽萍．基于多色集合理论的信息建模与优化技术[M]．北京：科学出版社，2010．