C8H4O5Na2·H2O脱水过程的热分析动力学研究

张国春， 狄燕青， 陈凤英， 乔成芳， 周春生

(商洛学院 化学与化学工程系 陕西省尾矿资源综合利用重点实验室， 陕西 商洛 726000)

0 引言

基于芳香环的刚性结构及羧基丰富多样的配位模式,芳香多元羧酸特别是间苯二甲酸近年来被大量应用于构筑包合物、多孔配位聚合物及多孔材料[1,2].由于间苯二甲酸的水溶性差，在合成功能配合物时常常使用间苯二甲酸类化合物的钠盐.文献[3]在合成铽与5-氨基间苯二甲酸配合物时加入了氢氧化钠，实际上是利用了5-氨基间苯二甲酸的钠盐，文献[4]也是利用中间体钠盐来完成相应的研究.因此，中间体钠盐的热力学数据将成为芳香羧酸类配合物深入研究的“瓶颈”.本课题组已研究了一水合5-羟基间苯二甲酸钠的低温热熔、标准摩尔生成焓和标准摩尔溶解焓[5]，但关于该化合物的非等温热分解动力学还未见报道.

近年来，在线性升温条件下对固体物质的反应(包括物理变化等)动力学进行研究而形成的“非等温动力学”是热分析动力学研究最活跃的领域.但由于沿用了等温、均相体系的动力学理论和方程，其结果的可靠性一直受到争议.为了获得可靠的热分析动力学研究结论，“非模型等转化率法”逐渐引起了该研究领域的重视[6-10].即用不同加热速率下所测的多条热分析曲线同一转化率α处的数据，在不涉及动力学模式函数的前提下进行其他因子的计算.用获得的较为可靠的活化能Ea值对单个扫描速率法的结果进行验证，还可以通过比较不同α下的Ea值来核实反应机理在整个过程中的一致性.

本文应用DSC技术获得一水合5-羟基间苯二甲酸钠4个不同升温速率下的脱水过程曲线，利用多重扫描速率法，以“非模型等转化率法”为基础，采用9种积分法和微分法相结合的热分析动力学方法处理程序进行定量表征，得到了其脱水过程的动力学三因子(反应级数n、表观活化能Ea、指前因子A)及相应的动力学方程.

1 实验部分

一水合 5-羟基间苯二甲酸钠样品采用文献[5]方法制备并鉴定，组成为C8H4O5Na2·H2O.上海天平仪器厂CDR-4P差动热分析仪(上海天平仪器厂)；样重1 mg左右；升温速率分别为 5、10、15和20 K·min-1，静态空气气氛.

2 结果与讨论

由不同升温速率下样品脱水阶段的DSC实验数据得到T～α关系图，见图1所示.由图1取得的四条曲线同一转化率处的实验数据见表1.计算处理时采用的动力学计算方程如下：

Integral isoconversional non-linear equation [NL-INT0][7]

(1)

Integral isoconversional non-linear equation [NL-INT][7]

(2)

Flynn-Wall-Ozawa (F-W-O) equation[11]

(3)

Kissinger equation[12]

(4)

一般积分法[13]

(5)

普适积分法[14]

(6)

Mac Callum-Tanner法[15]

式中：α-分解分数；T-绝对温度；T0-DSC曲线偏离基线的起始点；Ea-表观活化能；β-升温速率；R-气体常数；A-指前因子；G(α)-机理函数.

方程(1)～(4)属“非模型等转化率法”的处理方程，即对多重扫描曲线同一转化率处的(β,T)数据组，利用方程可在不考虑模型函数的前提下计算得到样品分解阶段的表观活化能，即可实现动力学三因子的分离求解；方程(5)～(9)可对单条扫描曲线进行动力学三因子的同时求解.

将表1中的数据代入方程(1)～(4)，则可利用“非模型等转化率法”计算得到样品脱水阶段的表观活化能(表2)，计算结果Ea与转化率α的关系如图2所示.由计算结果可知：样品在转化率为17.7%～81.7%阶段内，脱水分解的表观活化能近似相等，其值可作为单条曲线分别处理时的参考.为了从众多可能的机理函数中找出最概然函数，以便确定反应所遵循的机理方程，分别用41种常见的动力学机理函数[18]代入计算方程(5)～(9)，对各单条实验曲线进行计算并进行线性回归处理，以表2的“非模型等转化率法”在17.7%～81.7%阶段内的Ea作为参考基础，可获得样品脱水过程的动力学参数：反应级数n、表观活化能Ea和指前因子A及最概然机理函数，计算结果见表3.所有计算采用自编C++程序，在计算机上完成.

对照最概然机理函数表[18]， 可知样品脱水阶段的机理为化学反应机理，其微分形式和积分形式分别为(1-α)2和(1-α)-1-1.将得到的最概然机理函数、表观活化能、指前因子等参数分别代入方程dα/dT=(A/β)exp(-E/RT)f(α)，可得其动力学方程为：

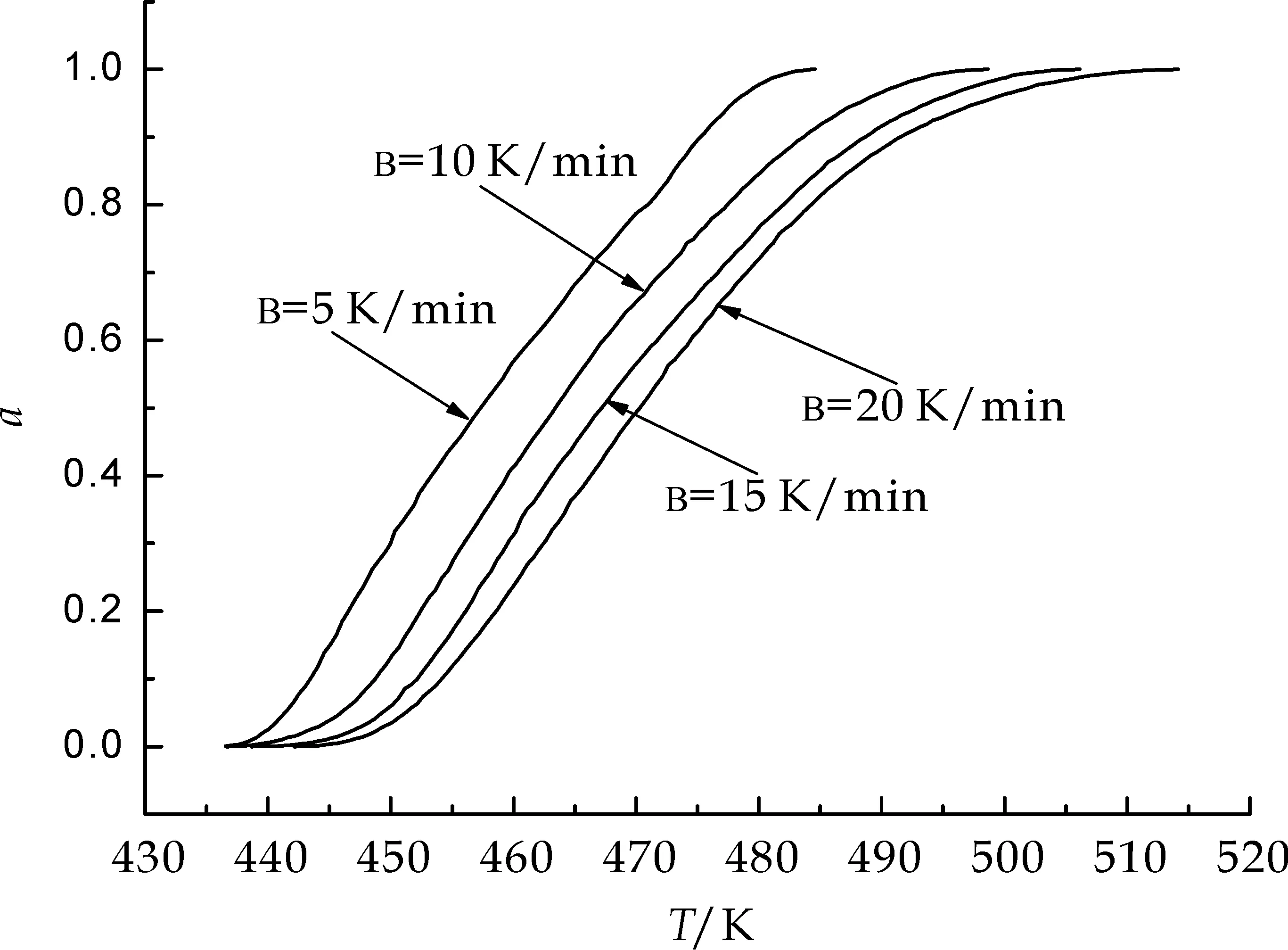
图1 样品不同升温速率下脱水分解过程的T～α关系图

序号αT/K(β=5 K/min)T/K(β=10 K/min)T/K(β=15 K/min)T/K(β=20 K/min)10.046 8441.32445.64449.05451.0520.102 2443.48448.88452.31454.2830.138 1444.73450.33453.93456.0840.177 1445.99451.76455.36457.8850.200 3446.58452.43456.25458.4260.216 4447.07453.02456.62459.1470.236 1447.79453.56457.34459.8580.262 0448.53454.65458.05460.9490.288 4449.59455.36458.96461.85100.297 9449.96455.71459.50462.56110.317 5450.33456.62460.05462.91120.334 1451.04456.99460.76463.46130.356 8451.93457.88461.12464.54140.373 0452.30458.42462.02465.26150.392 7453.04459.26462.92465.80160.415 5453.93460.22463.82466.80170.435 2454.65460.76464.40467.60180.458 0455.71461.65465.45468.68190.484 0456.70462.74466.34469.57200.500 5457.34463.28467.06470.31210.513 5457.88463.82467.77470.83220.543 0459.14465.08468.86472.11230.565 8459.85465.97469.94472.63240.585 5460.76466.71471.03473.72250.601 6461.54467.18471.75474.63260.614 6462.20467.97472.46475.17270.631 1462.91468.68473.18475.71

续表1

序号αT/K(β=5 K/min)T/K(β=10 K/min)T/K(β=15 K/min)T/K(β=20 K/min)280.660 3464.16470.12474.43477.15290.679 9464.89471.03475.35477.87300.699 6465.87471.92476.60478.95310.715 8466.51473.00477.32479.66320.739 0467.77474.09478.40481.10330.765 0468.92475.34479.84482.18340.787 8470.00476.60481.09483.63350.800 8471.00476.27482.18484.35360.817 3471.57478.40483.09485.24370.853 1473.18480.57485.07487.58380.875 9474.26481.83486.70489.75390.901 9475.34483.98488.84491.55400.957 4478.23488.84494.61499.10T0430.12435.50438.40440.01

表2 样品脱水阶段的非模型等转化率法表观活化能计算结果

续表2

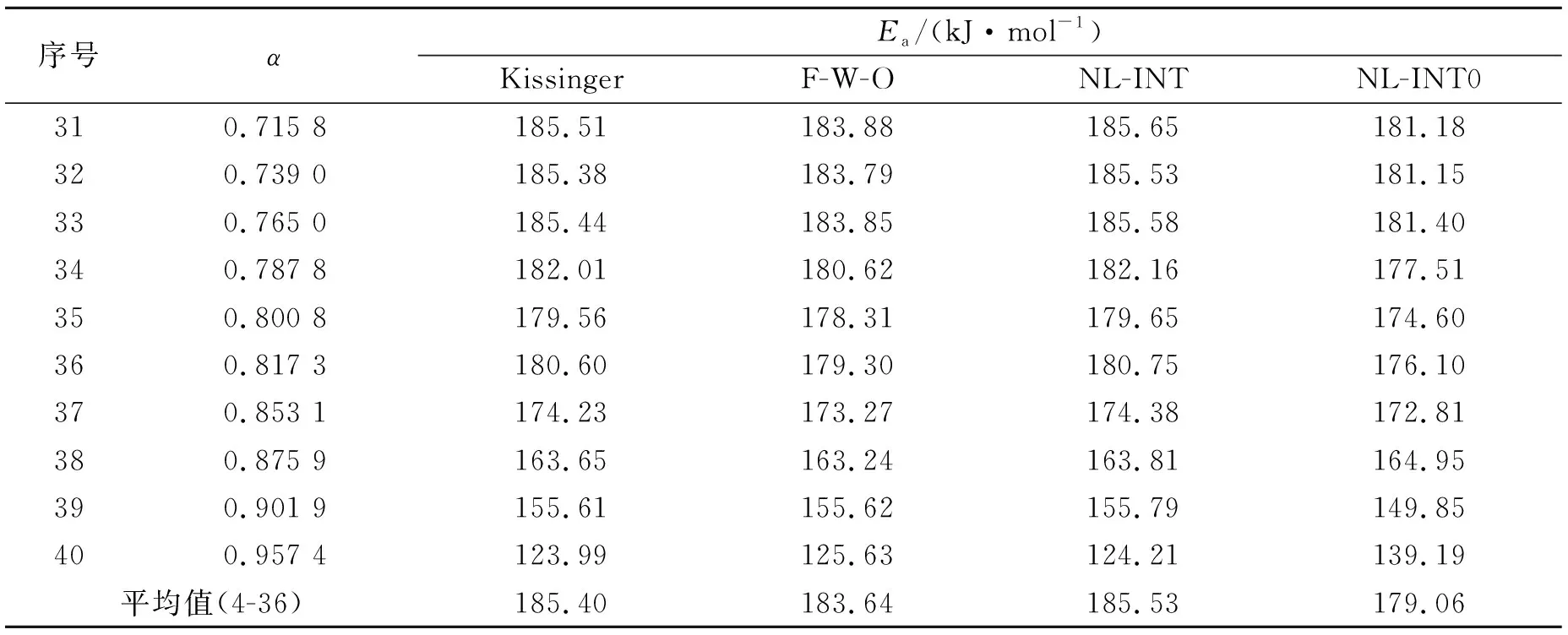
序号αEa/(kJ·mol-1)KissingerF-W-ONL-INTNL-INT0310.715 8185.51183.88185.65181.18320.739 0185.38183.79185.53181.15330.765 0185.44183.85185.58181.40340.787 8182.01180.62182.16177.51350.800 8179.56178.31179.65174.60360.817 3180.60179.30180.75176.10370.853 1174.23173.27174.38172.81380.875 9163.65163.24163.81164.95390.901 9155.61155.62155.79149.85400.957 4123.99125.63124.21139.19平均值(4-36)185.40183.64185.53179.06

图2 非模型等转化率法处理的样品脱水分解过程的Ea～α关系图

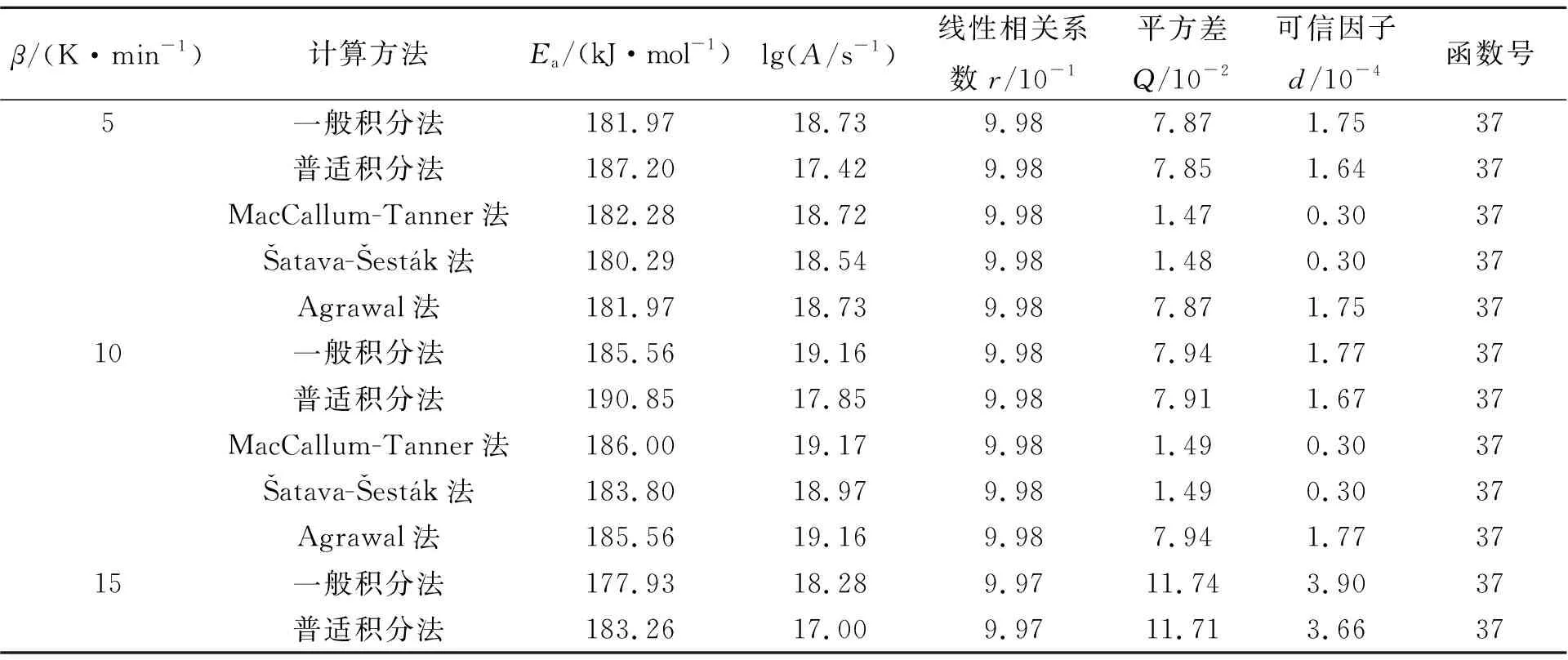
β/(K·min-1)计算方法Ea/(kJ·mol-1)lg(A/s-1)线性相关系数r/10-1平方差Q/10-2可信因子d/10-4函数号5一般积分法181.9718.739.987.871.7537普适积分法187.2017.429.987.851.6437MacCallum-Tanner法182.2818.729.981.470.3037Šatava-Šestk法180.2918.549.981.480.3037Agrawal法181.9718.739.987.871.753710一般积分法185.5619.169.987.941.7737普适积分法190.8517.859.987.911.6737MacCallum-Tanner法186.0019.179.981.490.3037Šatava-Šestk法183.8018.979.981.490.3037Agrawal法185.5619.169.987.941.773715一般积分法177.9318.289.9711.743.9037普适积分法183.2617.009.9711.713.6637

续表3

β/(K·min-1)计算方法Ea/(kJ·mol-1)lg(A/s-1)线性相关系数r/10-1平方差Q/10-2可信因子d/10-4函数号MacCallum-Tanner法178.3918.299.972.200.6737Šatava-Šestk法176.6118.139.972.200.6737Agrawal法177.9318.289.9711.743.903720一般积分法183.5118.919.993.900.4337普适积分法188.8617.629.993.880.4037MacCallum-Tanner法184.0518.939.990.730.0737Šatava-Šestk法181.9518.749.990.730.0737Agrawal法183.5118.919.993.900.4337平均值183.0718.48

3 结论

应用DSC技术获得一水合5-氨基间苯二甲酸钠4个不同升温速率下的脱水过程曲线，利用多重扫描速率法，以“非模型等转化率法”为基础，采用9种积分法和微分法相结合的热分析动力学方法处理程序，获得了脱水过程可信的动力学三因子，反应为化学反应机理,表观活化能Ea为183.07 kJ·mol-1，指前因子A为3.02×1018s-1，动力学方程为：

[1] 张旭衡.含胍基衍生物的超分子建筑及结构测定[D].广州：中山大学,2009:15.

[2] Chen S P,Ren Y X,Wang W T,et al.Nanoporous lanthanide-carboxylate frameworks based on 5-nitroisophthalic acid[J].Dalton Trans,2010,39:1 552-1 557.

[3] 李维芬,郑 倩,崔元靖,等.铽与5-氨基间苯二甲酸配合物的合成及发光性能[J].材料科学与工程学报,2009,26(1):40-42.

[4] 王晓玲.5-硝基间苯二甲酸稀土配合物的制备、结构和热力学性质[D].西安：西北大学,2010.

[5] 王竹君,陈三平,杨 奇,等.5-氨基间苯二甲酸钠和5-羟基间苯二甲酸钠的热力学性质[J].中国科学:化学,2010,40(9):1 378-1 386.

[6] 张国春,乔成芳,周春生,等.一水合5-氨基间苯二甲酸钠脱水过程的热分析动力学研究[J].陕西师范大学学报：自然科学版,2012,40(6):52-57.

[7] 胡荣祖,赵凤起,高红旭,等.非线性等转化率的微、积分法及其在含能材料物理化学研究中的应用-I.理论和数值方法[J].含能材料,2007,15(2):97-100.

[8] 王竹君.5-取代基间苯二甲酸类钠盐的热力学性质[D].西安：西北大学,2011:29-30.

[9] Brown M E,Maciejewski M,Vyazovkin S,et al.Computational aspects of kinetic analysis:Part A:The ICTAC kinetics project-data,methods and results[J].Thermochim Acta,2000,355(1/2):125-143.

[10] Budrugeac P.Differential non-linear isoconversional procedure for evaluating the activation energy of non-isothermal reactions[J].J Therm Anal Cal,2002,68:131-139.

[11] Flynn J H,Wall L A.A quick,direct method for the determination of activation energy from thermogravimetric data[J].J Polym Sci Part B, Polymer Letters,1966,4(5):323-328.

[12] Kissinger H E.Reaction kinetics in differential thermal analysis[J].Anal Chem,1957,29(11):1 702-1 706.

[13] Coats A W,Redfern J P.Kinetics parameters from thermogravimetric data[J].Nature,1964,201(4964):68-69.

[14] Hu R Z,Yang Z Q,Ling Y J.The determination of the most probable mechanism function and three kinetic parameters of exothermic decomposition reaction of energetic materials by a[J].Thermochim Acta,1988,123:135.

[15] Cameron G G,Fortune J D.Determination of activation energies from TGA and TVA traces[J].Eur Polymer J,1968,4:333-336.

[16] Skvara F,Sestak J.Computer calculation of the mechanism and associated kinetic data using a non-isothermal integral method[J].J Therm Anal,1975,8(3):477-489.

[17] Agrawal R K.A new equation for modeling nonisothermal reactions[J].J Therm Anal,1987,32(1):149-156.

[18] 胡荣祖,高胜利,赵凤起,等.热分析解动力学[M].2版.北京：科学出版社,2008:151-158.