压电陶瓷作动器非对称迟滞的建模与补偿控制*

赵小兴，姜 伟，李 巍

（华中科技大学数字制造装备与技术国家重点实验室，湖北武汉430074）

0 引言

压电陶瓷作动器是高精度定位中的关键部件，如扫描探针显微镜、扫描隧道显微镜、光学校准仪、金刚石车削机床和硬盘驱动器等［1］。它能满足纳米级定位精度，具有体积小、刚度高、响应快等优点。然而，它的响应位移与驱动电压之间存在着非对称迟滞特性，同时自身的蠕变和环境温度的变化也会造成其定位精度的漂移。

压电陶瓷作动器的非对称迟滞特性对其控制精度的影响十分显著。为减小或消除该不利影响，目前主要有两种解决途径：①电荷控制［2］，它需要特别设计的电荷驱动放大器，但该放大器价格昂贵，且存在漂移和过饱和等问题，因此极大地限制了其应用范围；②电压控制，需要建立非线性迟滞的数学模型，并通过逆模型前馈补偿来提高控制精度。电压控制逐渐成为压电陶瓷作动器精密控制的首选方案，其关键是非线性迟滞的精确建模。目前，国内外学者分别提出了多种迟滞模型，如Preisach 模型［3-4］、Prandtl-Ishlin⁃skii模型［5-6］、Maxwell模型［7］、极坐标模型［8］、Bouc-Wen模型［9-10］等。Preisach模型通过对迟滞因子的双重积分来逼近迟滞特性，由于模型中含有二次积分项，导致计算效率低，难以应用于实时系统。Prandtl-Ishlinskii模型是对Preisach 模型的改进，它由多个PI 算子加权叠加组成，建模的计算量较大且容易产生毛刺。Maxwell模型采用输出力和滑块位移模拟压电陶瓷的驱动电压和响应位移，须增加弹簧滑块的数目以提高模型精度，由此导致求解过程复杂、计算量大。极坐标模型采用椭圆曲线的极坐标方法，在获得主迟滞环模型前提下，再根据一定的递推公式，得到次迟滞环模型。

Bouc-Wen模型（简称B-W模型）是利用一个具有不确定参数的非线性微分方程来描述迟滞特性，通过选择合适的参数，可以得到各种形状的迟滞环。由于它只需要用一个辅助的非线性微分方程来描述迟滞行为，因而该方法计算效率高，实时性好，且逆模型求解十分方便。但是传统B-W 模型是一个关于中心点严格对称的模型，对于非对称迟滞特性的拟合精度有限。

本研究基于传统B-W模型，提出一种改进的B-W模型来表征压电陶瓷作动器的非对称迟滞特性，针对压电陶瓷作动器的非对称迟滞特性，分别基于传统B-W模型和本研究所提的改进B-W模型，对比研究前馈补偿、前馈加PI反馈补偿两种控制方法的效果。

1 改进B-W 模型

1.1 传统B-W模型

传统B-W模型是由Bouc提出并由Wen改进的一种微分方程，它用于描述压电陶瓷作动器迟滞非线性的微分方程为：

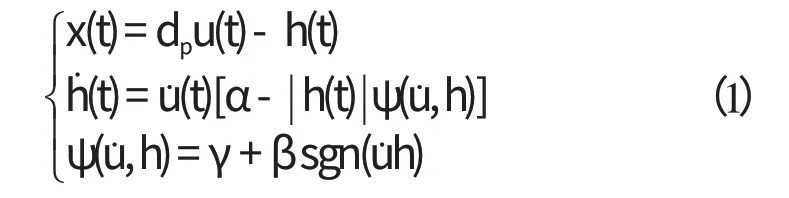
式中：x(t)—压电陶瓷输出位移；u(t)—压电陶瓷输入电压；h(t)—迟滞变量；ψ(,h)—形状控制函数；dp—压电系数；α,β,γ—形状控制参数。

由于模型参数的限制，传统B-W模型的形状控制函数只有两个自由度(γ-β,γ+β)，它是关于中心点严格对称的，ψ(,h)特性图如图1所示。如果直接用它描述非对称迟滞现象，很难达到较高的拟合精度。

1.2 改进B-W模型

实验测试结果表明，压电陶瓷作动器的输出位移与输入电压之间存在着较强的非对称迟滞特性。因此，采用传统B-W模型很难达到较高的拟合精度。为了提高模型精度，研究者必须对传统B-W模型进行改进，使其能够模拟非对称性迟滞特性。由前文分析得知，传统B-W 模型的形状控制函数只有两个自由度，其中只有β的符号在不同象限内发生变化，而γ的大小不会影响形状控制函数自由度的数目。因此，为了增加自由度，本研究假设γ=0，并将βsgn(h)变换成βsgn(h)+ϕsgn()+φsgn(h)，具体微分方程为：

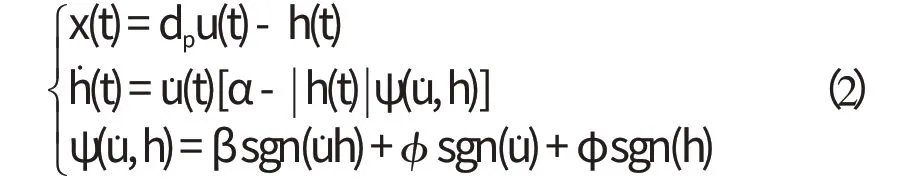
式中：α,β,ϕ,φ—形状控制参数；x(t),u(t),h(t),ψ(,h),dp—含义与式（1）相同。

改进后的形状控制函数有4个自由度( -β-ϕ+φ,β+ϕ+φ, -β+ϕ-φ,β-ϕ-φ)，它既可以模拟对称迟滞，也可以模拟非对称迟滞，如图1所示。因此，与传统B-W 模型相比，用改进B-W 模型来描述非对称迟滞特性能够达到更高的精度。

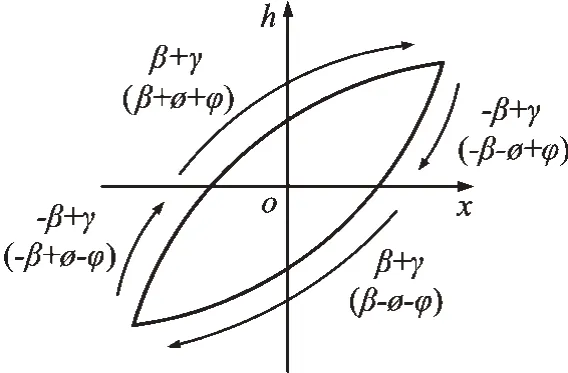
图1 ψ(,h)特性图

2 模型参数辨识

2.1 基于粒子群算法的模型离散化

由式（2）可知，改进B-W 模型是由5 个参数决定的，它们分别是：dp、α、β、ϕ、φ，这5个参数为本研究需要辨识的参数。目前，辨识模型参数的方法有很多，如最小二乘法、卡尔曼滤波法、差分进化法、遗传算法、粒子群算法等。文献［11］指出，与遗传算法相比，粒子群算法容易实现且调节参数少，此外它对计算机的内存和CPU的速度要求较低，故本研究选用粒子群算法进行参数辨识。

为了提高粒子群优化算法的计算效率，避免反复求解微分方程，将式（2）所示的改进B-W 模型离散化如下：

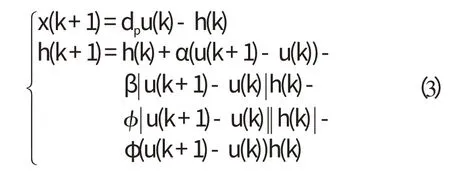
本研究采用Shi 与Eberhart 提出的一种带惯性权重的粒子群算法，其进化方程为：

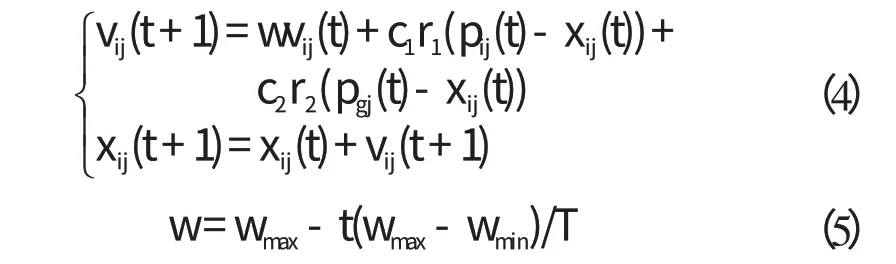
式中：N—种群规模；D—粒子维数；i=1,2…N,j=1,2…D；其他参数的含义详见文献［12］。

本研究选用模型仿真位移xBW与实测位移xr的均方根误差eRMS作为适应度函数，具体形式如下：

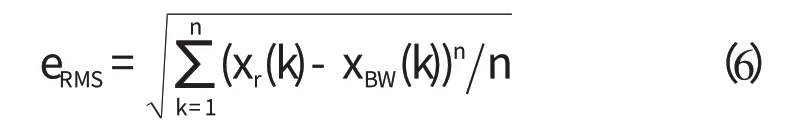
式中：n—采样点数。

2.2 模型参数辨识结果

在辨识模型参数前，首先需要通过实验测试得到一组压电陶瓷作动器的电压—位移曲线，再利用该曲线进行参数辨识。本研究首先由NI-PXI 测试平台产生一个正弦信号u(t)=5+5sin(0.2πt-π/2)，经过驱动电源放大处理（放大倍数为15倍），输出给压电陶瓷作动器（PST 150），压电陶瓷作动器产生伸缩变形，并由激光位移传感器（LK30，分辨率为10 nm）获取该伸缩信号，同时由NI-PXI 测试平台将信号采集（采样频率为100 Hz）并保存下来。本研究对采集到的信号，进行粒子群优化算法辨识，即可得到改进B-W模型5个参数的最优解：dp=0.1126μm/V ,α=0.0473μm/V ,β=0.0998V-1,ϕ=-0.0977V-1,φ=-0.0028V-1(其中,eRMS=0.121 7)。利用同样的数据和粒子群优化算法，即可得到传统B-W 模型4 个参数的最优解：dp=0.0709μm/V ,α=0.0226μm/V ,β=0.0420V-1,γ=-0.0172V-1(其中,eRMS=0.3173)。

实测迟滞曲线、传统B-W 模型迟滞曲线和改进B-W模型迟滞曲线的对比如图2所示。为了比较上述两种模型的拟合精度，本研究选用了实测位移相对于仿真位移的下述3个评价指标：均方根误差eRMS、平均绝对误差|e|mean、最大绝对误差|e|max。实测位移相对于上述两种模型的仿真位移的误差对比情况如表1所示。

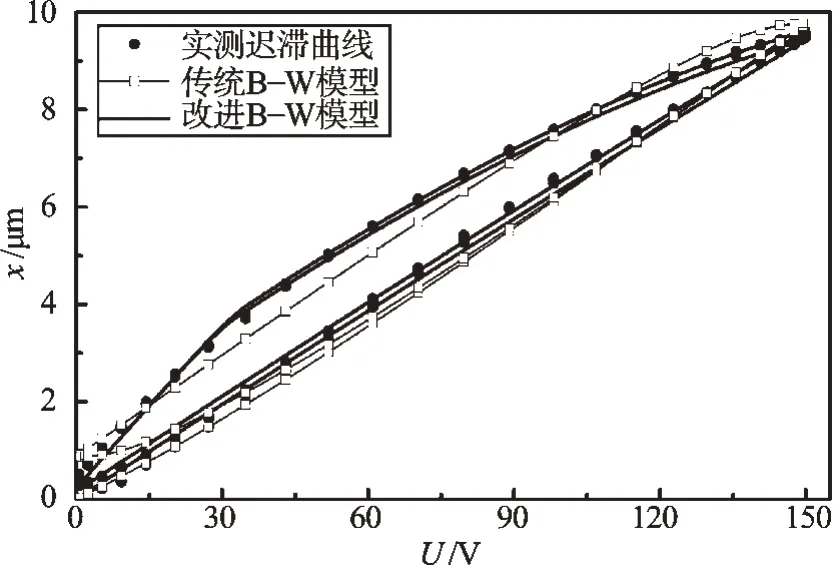
图2 迟滞曲线的拟合

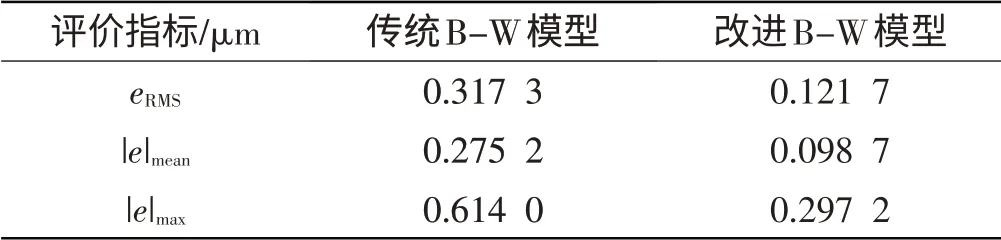
表1 仿真拟合误差比较

观察图2 和表1 可知，改进B-W 模型的拟合误差要明显小于传统B-W模型，原因在于传统B-W模型是关于中心点严格对称的，它只能用来模拟对称迟滞特性，然而改进B-W 模型却能够模拟非对称迟滞特性，更适用于模拟压电陶瓷作动器的非对称迟滞特性。

3 非对称迟滞的补偿控制

3.1 前馈补偿控制

本研究对压电陶瓷作动器的迟滞补偿是基于逆模型的前馈控制，即在实际压电系统中串入迟滞特性的逆模型作为补偿器，实现对迟滞非线性的补偿。

基于逆模型的前馈迟滞补偿原理如图4中的虚线框所示。设定期望轨迹xd(t)=4.5+4.5 sin(0.2πt-π/2)，经过迟滞补偿器计算出压电陶瓷作动器的控制电压u(t)=[xd(t)+H(t)]/dp，控制电压u(t)激励压电陶瓷作动器产生伸缩变形，采集实际输出轨迹xr(t)，用于评价其与期望轨迹xd(t)的误差e(t)=xr(t)-xd(t)。

本研究分别采用传统B-W模型和改进B-W模型进行前馈补偿控制实验，以便对比改进B-W模型对于前馈补偿控制的改善效果。期望运动轨迹和采用上述两种模型进行前馈补偿控制的实际输出运动轨迹及其轨迹跟踪误差如图3所示。其中，跟踪误差的均方根值eRMS、平均绝对值|e|mean、最大绝对值|e|max的对比如表2所示。实验结果表明：与采用传统B-W模型进行前馈补偿控制相比，采用改进B-W模型可使误差降低约42%。

3.2 前馈+PI反馈补偿控制

在上一节中，经过逆模型前馈补偿，迟滞现象虽然得到了明显抑制，但是对于高精密位移控制，其控制精度仍然不足。为了进一步提高控制精度，本研究在前馈补偿的基础上，引入比例—积分（PI）反馈控制，其控制原理如图4所示。

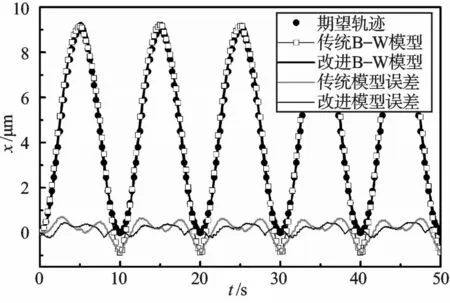
图3 前馈补偿控制的运动轨迹与误差

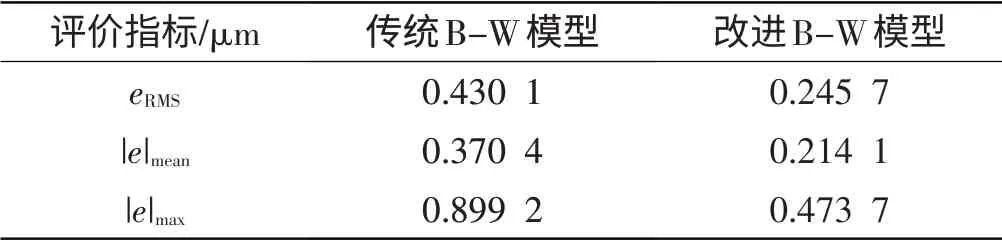
表2 前馈补偿控制误差比较

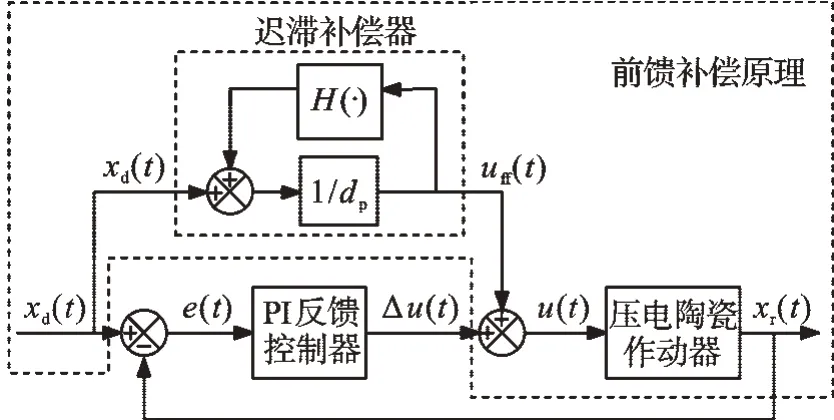
图4 前馈补偿结合PI反馈控制原理

首先，在实验前用传统B-W 模型作前馈补偿，用改进B-W 模型代替图4 中的压电陶瓷作动器进行仿真，仿真中不断调节参数Kp、Ti的大小，观察误差e(t)的变化，确定Kp和Ti的调节范围。其次，在实验过程中，参考仿真时确定的参数调节范围，可以很快得到较为理想的Kp和Ti值，从而达到较高的控制精度。

本研究采用上述两种模型进行前馈补偿加PI反馈控制的轨迹跟踪误差的对比如图5所示，其误差的均方根值eRMS、平均绝对值|e|m ean、最大绝对值|e|max的对比如表3所示。实验结果表明：①与单纯采用前馈控制相比，采用前馈加PI反馈控制可将控制精度提高大约一个量级；②与采用传统B-W模型进行前馈加PI反馈补偿控制相比，采用改进B-W模型可使误差降低约20%。

4 结束语

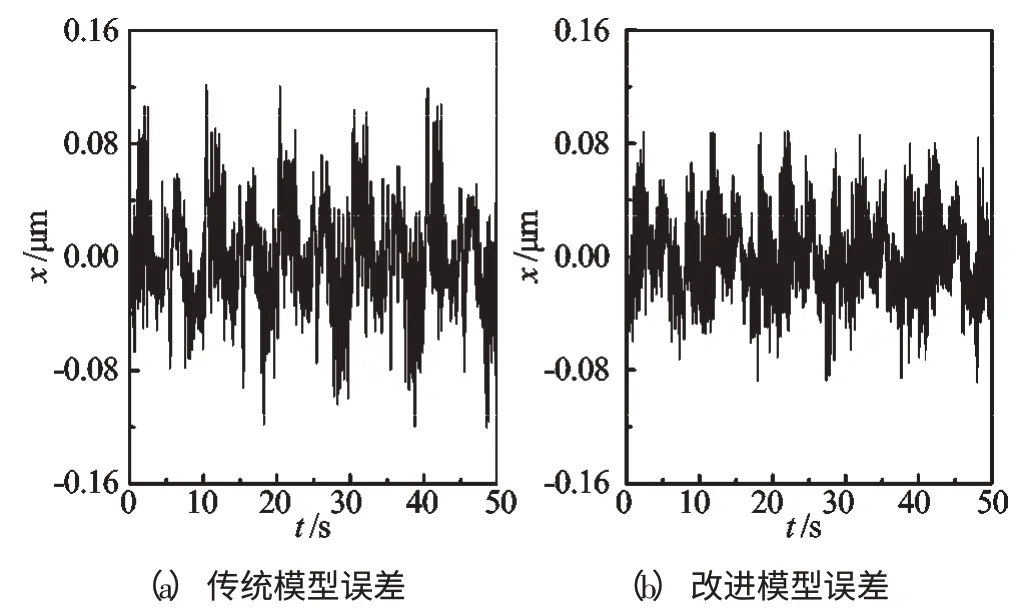
图5 前馈补偿结合PI反馈控制的轨迹误差

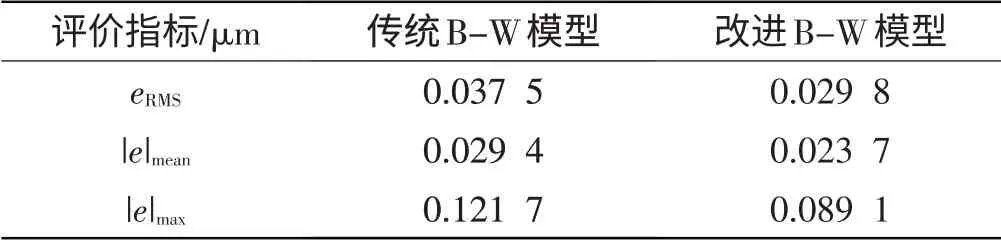
表3 前馈+PI反馈补偿控制误差比较

针对传统B-W 模型不能准确描述压电陶瓷作动器迟滞的非对称性问题，本研究提出了一种改进的B-W 模型，并采用粒子群优化算法辨识出了模型参数。在相同的电压输入条件下，仿真与实验结果比较显示，改进B-W 模型的位移输出误差小于传统B-W模型，表明改进B-W模型对于压电陶瓷作动器非对称迟滞特性的描述精度更高；在相同的期望轨迹输入条件下，分别采用传统B-W 模型和改进的B-W 模型进行前馈补偿控制实验，以及前馈加PI反馈补偿控制实验。实验结果表明在相同的控制方式下，采用改进B-W模型可得到更高的轨迹跟踪精度，并且采用基于改进B-W模型的前馈加PI反馈控制效果更好。

（References）：

［1］LEANG K K，DEVASIA S.Design of hysteresis- compen⁃sating iterative learning control for piezo-poitioners：applica⁃tion to atomic force microscopes［J］.Mechatronics，2006，16（3-4）：141-158.

［2］SALAH M H，MCLNTYRE M L，DAWSON D M，et al.Charge feedback-based robust position tracking control for piezoelectric actuators［J］.IET Control Theory Applica⁃tion，2012，6（5）：615-628.

［3］WOLF F，SUTOR A，RUPITSCH S J，et al.A generalized Preisach approach for piezoceramic materials incorporating uniaxial compressive stress［J］.Sensors and Actuators A：Physical，2011，18（4）：1-7.

［4］党选举，谭永红.在Preisach 模型框架下的似对角动态神经网络压电陶瓷迟滞模型的研究［J］.机械工程学报，2005，41（4）：7-12.

［5］JANAIDEH M A，RAKHEJA S，SU C Y.A generalized Prandtl-Ishlinskii model for characterizing the hysteresis and saturation nonlinearities of smart actuators［J］.Smart Materials and Structures，2009，18（4）：1-9.

［6］JIANG Hao，JI Hong-li，QIU Jin-hao，et al.A modified prandtl-ishlinskii model for modeling asymmetric hystere⁃sis of piezoelectric actuators［J］.IEEE Transactions on Ultrasonics，Ferroelectrics and Frequency Control，2010，57（5）：1200-1210.

［7］JUHASZ L，MAAS J，BOROVAC B.Parameter identifica⁃tion and hysteresis compensation of embedded piezoelectric stack actuators［J］.Mechatronics，2011，21（1）：329-338.

［8］王希花，郭书祥，叶秀芬，等.压电陶瓷迟滞特性的建模及复合控制［J］.电机与控制学报，2009，13（5）：766-771.

［9］RAKOTONDRABE M.Bouc-Wen modeling and inverse multiplicative structure to compensate hysteresis nonlineari⁃ty in piezoelectric［J］.Automation Science and Engineer⁃ing，2011，4（2）：428-431.

［10］王代华，朱 炜.WTYD型压电陶瓷微位移器的迟滞特性建模与实验验证［J］.光学精密工程，2010，18（1）：205-211.

［11］MONTAZERI A，POSHTAN J，YOUSEFI-KOMA A.The use of 'particle swarm' to optimize the control system in a PZT laminated plate［J］.Smart Materials and Struc⁃tures，2008，17（4）：1-7.

［12］VALLE Y D，VENAYAGAMOORTHY G K，MOHA⁃GHEGHI S，et al.Particle swarm optimization：basic con⁃cepts，variants and applications in power systems［J］.IEEE Transactions on Evolutionary Computation，2008，12（2）：171-195.