九曲江大桥吊杆张拉力的优化
2013-01-18聂子涵
聂子涵 李 民
(重庆交通大学土木建筑学院,重庆 400074)
1 工程实例概况
本文采用的工程为九曲江大桥,桥梁全长176.1 m,位于博鳌核心区沙美内海旅游道路设计起点在培兰村南侧,为三跨简支钢管混凝土系杆拱桥。本桥采用刚性系杆刚性拱,柔性吊杆。拱轴线为二次抛物线,矢跨比为1/4,边拱矢高11.9 m,中拱矢高16.9 m。桥跨布置如下:50 m+70 m+50 m=170 m。桥面布置为:3 m(人行道)+2 m(拱肋)+3 m(非机动车行道)+1 m(护栏)+8 m(机动车行道)+1 m(护栏)+3 m(非机动车行道)+2 m(拱肋)+3 m(人行道),总宽26 m。拱肋采用圆端型钢管混凝土,中拱钢管宽160 cm,拱肋高为140 cm,钢管及腹板壁厚1.8 cm,内充C50微膨胀混凝土,边拱钢管宽160 cm,拱肋高为120 cm,钢管及腹板壁厚1.8 cm,内充C50微膨胀混凝土。系杆吊杆处高为188 cm,底宽为300 cm,壁厚100 cm,采用箱形断面。系杆和横梁为预应力混凝土结构。边拱每片拱肋设吊杆9根;中拱每片拱肋设吊杆13根,吊杆间距为4.6 m。桥面2%横坡通过横梁高度的变化进行调整;桥面板采用整体式实心板,厚25 cm。风撑采用桁架风撑。
钢束张拉时以张拉力为主,张拉力与伸长量双控,测量的钢绞线伸长量允许±6%的误差,张拉伸长量从零张拉应力起算。设计图中所列伸长量值均指锚下至锚下段钢束长度计算值,不包含千斤顶工作长度。预应力钢束在钢束锚固面张拉,根据施工规范规定,张拉完毕后14 d内必须压浆。钢束应张拉一批压浆一批,待压浆强度达到90%以上时,才可进行下一道工作。九曲江大桥中跨梁、拱布置图见图1。

图1 九曲江大桥中跨梁、拱布置图(单位:cm)
2 吊杆张拉力优化方法的提出
目前,确定钢管混凝土系杆拱桥成桥状态的吊杆张拉力所使用的方法是斜拉桥的索力优化理论。但是两者却有着多方面的不同。第一,两者的整体受力状态不同。对于主梁受力一般属于压弯构件的斜拉桥来说,它的桥面结构会相对比较柔和,而对于系杆拱桥,拱肋的刚度与系梁的刚度接近,桥面结构呈刚性状态,主梁属于拉弯构件。第二,斜拉桥非线性影响较大,它在主塔高度,拉索长度,以及拉索与水平面的夹角等各个方面都与系杆拱桥有很大差异。第三,系杆拱桥在施工过程中,吊杆张拉的调整比较复杂,需要经过多次张拉到目标力。而由于系杆拱桥在施工方面的复杂性,对于使用不同施工方法的系杆拱桥,其张拉的次数和大小也各不相同。这与斜拉桥拉索的张拉方式有着很大的不同。综合以上各个方面,直接引用斜拉桥的拉索理论来进行系杆拱桥的吊杆张拉力的计算显然并不合理。对于本文来说,九曲江大桥的吊杆张拉力优化,计算中仅考虑恒载作用下的优化。从目前的研究成果来看,正确计算出作为传递构件的吊杆的内力的方法主要有以下几种:刚性支承梁法,刚性吊杆法。而对于以九曲江大桥作为背景的本文,在计算中就以系梁的线形,拱肋弯矩作为控制目标来确定成桥状态时吊杆合理张拉力,并对这两种方法的优缺点进行分析比较。
3 九曲江大桥吊杆张拉力优化方法的分析
3.1 刚性支承梁法计算吊杆张拉力
为了达到让吊杆和桥面系连接处的节点在成桥状态时受到恒载和吊杆张拉力作用的位移为零的目的,同时让纵梁内弯矩理解为刚性支承梁弯矩,使用刚性支承梁法来求解一组恒载的张拉力值。在求解九曲江大桥时,考虑的主要是主梁线形,兼顾吊杆的内力,拱肋弯矩等。具体方法为首先建立九曲江拱桥的模型,然后在吊杆与纵梁的连接处用刚性支承来代替吊杆,求解此时恒载作用下这些刚性支承处的支座反力,即为吊杆力。结合MIDAS计算软件,得到刚性支承梁法求得九曲江大桥的吊杆张拉力见表1。

表1 刚性支承梁法计算吊杆张拉力 t
从表1看出,在拱脚与桥面连接处的边界条件复杂,按照此法计算出的1号吊杆力达到了175.5 t。这是由于为了使这个位置附近的吊杆与纵梁连接处变形为零就必须要施加很大的吊杆张拉力。再通过图2~图4可以看出,对于九曲江大桥结构来说,在跨中的系梁弯矩最大,达到8.49×103kN·m,在梁端的系梁弯矩最小,为-1.54×104kN·m。而对于拱肋弯矩,最大最小值分别为5.74×102kN·m和-4.91×102kN·m,分别发生在拱顶处和拱脚处。对于拱桥的受力来说,变化不是很大,满足要求。
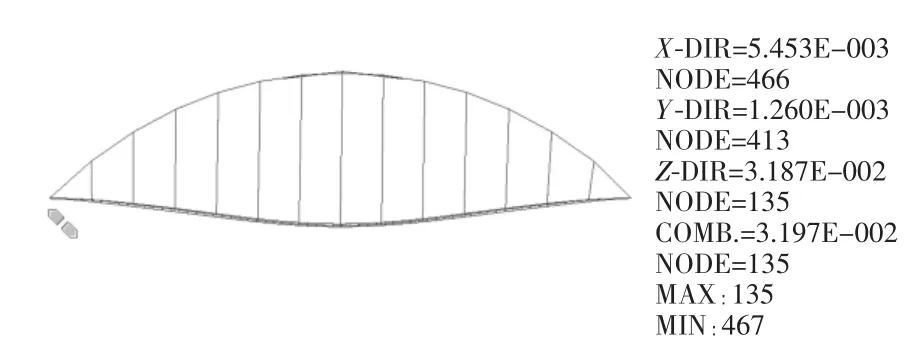
图2 中跨竖向位移(一)

图3 中跨系梁弯矩(一)

图4 中跨拱肋弯矩(一)
3.2 刚性吊杆法确定吊杆张拉力
刚性吊杆法与刚性支承梁法有很大的不同。刚性吊杆法把拱作为主要的研究对象。要实现整体的受力优化,我们就应该尽量让拱肋来承担恒载,这就充分利用了拱作为受压构件它的受压潜力很大的特点。通过这样的分配,就能使桥面系和拱肋的变形相互协调,使得拱与桥面系相应吊杆节点位移差为零。作为拱梁组合,改变吊杆张拉力的大小来协调两者之间的关系,从而获得比较合理的全桥受力状态。具体在计算时,取吊杆的轴向刚度很大,并且不计吊杆的容重来确定吊杆力的大小。在进行了如上设定后,通过对吊杆力的优化调整,使得拱肋的弯矩及拱桥变形得到调节,把在恒载作用下产生的九曲江大桥的初始刚度矩阵所产生的各处吊杆与桥面连接处的节点位移进行整理,最后能够使得成桥状态时的结构内力达到设计者的要求。根据以上方法,利用MIDAS可以得到刚性吊杆法求得的吊杆力,结果见表2。

表2 刚性吊杆法计算吊杆张拉力 tof
由表2可看出,刚性吊杆法确定的张拉力相对于刚性支承梁法更为合理,各根吊杆力比较均匀。
对于九曲江大桥结构自身而言,从图5~图7可以看出系梁最大弯矩发生在跨中处,最大值为6.92×103kN·m,最小弯矩发生在梁端处,最小值为-1.21×103kN·m。拱肋弯矩最大最小值分别为6.44×102kN·m,-5.30×102kN·m,分别发生在拱顶处及拱脚处,变化不大从而满足受力要求。

图5 中跨竖向位移(二)

图6 中跨系梁弯矩(二)

图7 中跨拱肋弯矩(二)
4 结语
从上面的分析研究中可以看出,对于九曲江拱桥采用刚性支撑梁法,刚性吊杆法两种方法调整后,看出刚性支承梁法在吊杆力的计算上具有明显的缺陷,从系梁弯矩图和拱肋弯矩图可以看出,无论是拱肋和系梁关键部位,它们的差别均不太大,综合考虑,建议采用刚性吊杆法。
[1] 叶梅新,许润锋,谢晓慧.确定系杆拱桥吊杆索力张拉值的方法[J].交通科学与工程,2010,26(1):59-60.
[2] 盛兴旺,李松报.确定系杆拱桥吊杆力的刚性连续梁法算法[J].铁道科学与工程学报,2009,6(3):78-80.
[3] 江旭东.确定系杆拱桥吊杆初始张拉力方案及施工控制[J].上海公路,2008(1):7-9.
[4] 钟健聪,李新平.空间系杆拱桥吊杆张拉控制的研究[J].广东公路交通,2004(2):91-93.
[5] 陈金巧,姚国文.恒载作用对系杆拱桥短吊杆空间受力行为的影响[J].科技视界,2003(4):59-61.
[6] 顾安邦,孙国柱.拱桥[M].北京:人民交通出版社,1994.
