基于改进SIFT的图像拼接算法

崔得龙 ， 弓云峰 ， 左敬龙

（1.广东石油化工学院 计算机与电子信息学院，广东 茂名 525000；2.广东省石化装备故障诊断重点实验室 广东 茂名 525000）

图像拼接是基于图像绘制技术（IBR）中的一种基本的处理方法，所谓图像拼接就是将多幅相互间存在重叠的序列图像进行无缝拼接，合成一幅包含各图像信息的、宽视角场景的高清晰图像，是目前计算机视觉、图像处理和虚拟现实等领域的研究热点。

图像配准问题是图像拼接技术的关键技术之一。目前主要的图像配准方法可分为基于灰度信息的图像配准方法[1]，基于特征的图像配准方法[2]和基于变换域的图像配准方法[3]等。其中最常用的是基于图像特征的配准方法：首先对待拼接图像进行特征提取得到特征点集，并通过相似性度量找到匹配的特征点对，然后匹配计算得到图像空间坐标变换参数，最后进行图像配准，特征提取和特征匹配是配准技术的关键。

传统的特征提取方法如Harris角点算法、基于边缘的特征提取算法等对于图像配准的条件要求很高，当图像间发生尺度缩放、旋转和光照变换以及仿射变换等情况时，匹配效果就会受到严重的影响。目前去除误匹配的方法多采用极几何约束、迭代求精，如 M-estimators[4]、RANSAC[5]等方法，但这些方法受初匹配内点（正确匹配的点）比例影响较大，如何提高内点的比例常常决定着匹配图像的配准精度和迭代效率。文献[6]利用欧氏距离通过调整最近邻（NN）与次近邻（SCN）距离的比值阈值，可以减少一些误匹配，但同时也易损失一部分原本正确的匹配点，不能在真正意义上提高正确匹配率。文献[7]提出一种基于中值滤波的特征点对匹配算法，能部分但不能完全剔除错误匹配的特征点对，同时该方法执行效率较低。文献[8]提出把中值滤波用于检测RANSAC的初始迭代特征点对，但并没有考虑排除错误的特征点对，因此对RANSAC的执行效率没有实质的改进。

针对目前基于SIFT的图像拼接算法复杂度较高和特征点匹配不准等问题，提出了一种基于改进SIFT的图像拼接算法。算法利用改进的SIFT进行特征提取，降低了算法的复杂度，同时采用模拟退火算法进行特征点匹配，从而估计出几何变换的参数。实验结果表明，该方法对图像间存在的平移、旋转、明暗强度和噪声干扰都具有良好的鲁棒性，可实现高质量的图像拼接。

1 SIFT特征提取

1.1 SIFT

2004年David G.Lowe提出了一种基于尺度空间的，对图像旋转、缩放甚至仿射变换保持不变的图形局部特征算子—SIFT（Scale Invariant Feature Transform）。 SIFT算子不仅能提取出大量稳定的特征点，而且其独特性较高的特征描述符在大多数情况下也能保证较高的匹配率[9]。SIFT算法特征点提取具体步骤如下：

1）构造高斯差分尺度空间（DOG），检测尺度空间极值点

为了得到多尺度空间内的稳定关键点，利用不同尺度的高斯差分核与图像进行卷积构成高斯差分尺度空间。

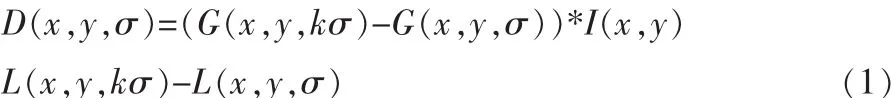
检测尺度空间的极值点，每个检测点和它同尺度的8个相邻点以及上下相邻尺度的个点进行比较，以确保在尺度空间和二维空间都能检测到极值点，DOG尺度空间极值检测如图1所示。

图1 DOG尺度空间局部极值检测Fig.1 Local Key-point detection of DOG scale space

2）极值点精确定位

通过拟合三维二次函数精确定位极值点的位置和尺度，同时去除低对比度的点和不稳定的边缘响应点。边缘响应点通过式（2）去除。

式中，H为的Hessian矩阵，r为控制特征值大小的参数。

3）分配关键点方向

为使SIFT特征点具备局部旋转不变性，利用关键点邻域梯度像素的分布特性为每个关键点分配方向参数，点处梯度的模和方向的公式如式（4）和式（5）。

其中L的取值为每个关键点所在的尺度。实际中，在以关键点为中心的邻域窗口内采样，并用直方图统计邻域像素的梯度方向，直方图的峰值代表了该特征点处邻域梯度的主方向，即为该特征点的主方向。

4）生成特征点描述符

首先将坐标轴旋转为关键点的主方向，以确保旋转不变性，然后以关键点为中心取的窗口均匀地分为16个的小块，在每个小块的 8 个方向 （0°，45°，90°，135°，180°，225°，270°，315°）的梯度直方图上绘制每个梯度方向的累加值，形成一个种子点，则每个种子点含有8个方向的信息向量。一个特征点用16个种子点描述，即由128维向量来描述。

1.2 改进的SIFT特征点描述符

在SIFT提取的第（3）步，需要为特征点分配一个主方向，通过主方向旋转特征点的局部区域实现特征点的抗旋转能力。考虑到圆具有很好的旋转不变性，因此文献[10]提出利用特征点周围的圆形区域来构造SIFT特征描述子，当图像产生旋转时，仅子环内的像素位置发生了变化，其余特性基本保持不变，如图2所示，具体构造过程如下：

首先，计算圆环内各像素的梯度值和方向，统计出8个方向的梯度累加值。其次，将梯度累加值从大到小进行排序，以保证旋转后排序值的不变性。最后，将该向量进行归一化处理，减少光照变化对特征描述符的影响。改进的SIFT描述符本身具有旋转不变性，不需要通过坐标轴的旋转来确保特征描述符的旋转不变性。同时，改进的SIFT描述符从原来的128维向量降低到64维，有效提高了算法的运行效率，降低了特征点的匹配复杂度。

图2 改进的SIFT特征点描述符生成过程图Fig.2 Flow of improved SIFT feature point

2 特征点匹配

对于需要进行拼接的两幅图像，按照相同的SIFT特征点提取方法，可以分别得到它们的特征点集，记为P={pj=（pj1，pj2）T|j=1，2，…，m}和 Q={qj=（qj1，qj2）T|j=1，2，…m}。 则集合 P和Q之间由仿射变换（A，t）关联。定义匹配矩阵M，其元素mjk满足条件此时点集匹配的问题可被重新定义为：对于给定的点集P和Q，求出仿射（A，t）变换或匹配矩阵M，使得匹配达到最优。按照Gold所提出的方法，对于给定的两个点集P和Q的匹配问题可以看作为求解下面目标函数的最小化状态[11]。

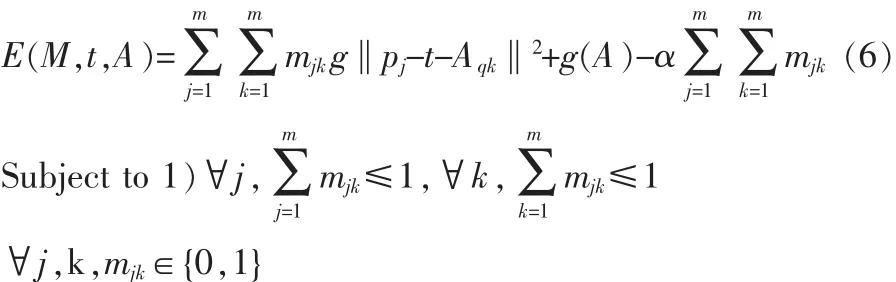
2）g（A）=γ（a2+b2+c2）

此时特征点匹配问题就转化为联合求解匹配矩阵和变换参数的优化问题。为避免目标函数式（6）落入局部极小，将二值的匹配矩阵转化为连续实数矩阵，即 mjk∈{0，1}→mjk∈[0，1]。

式中对M行和列的约束是不等式，通过引入一松弛变量，可以将不等式约束转化为等式约束。

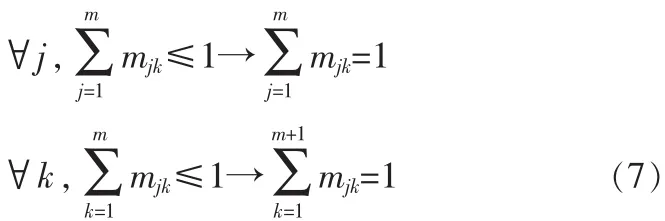
为了求解目标函数（6），选用模拟退火算法进行全局最小值求解。在确定性模拟退火算法中，当温度足够高时，能够很容易求出目标函数的全局最小值。根据优化理论，目标函数应该凸化，为此引入一个阻尼项其中 T是控制模拟温度，这个阻尼项的作用是：

1）在高退火温度下，使目标函数凸化，其凸度由模拟温度T控制；

2）确保匹配矩阵所有的元素非负。

将匹配矩阵的等式约束式（7）和阻尼项加到目标函数式（6）中，可以得到新的特征点匹配问题的目标函数如下所示：

其中 μj和 υk是 Lagrange因子。

通过最小化目标函数（8）可以得到匹配矩阵和点集P和Q之间的变换参数。

3 图像拼接

算法性能验证以Matlab R2007为实验平台，选用两幅标准测试图像进行图像拼接验证，测试图像分别如图3（a），（b）所示。

3.1 图像拼接

具体图像拼接步骤如下：

1）SIFT特征点提取，分别对需要进行拼接的两幅图像提取SIFT特征点集合；

2）按照第2节的方法对提取的特征点集合进行特征点匹配，估计出两幅图像的几何形变参数及图像间的重叠区域，SIFT特征点匹配结果如图3（c）所示；

3）以拼接后的图像尺寸大小，生成一幅区域图像。将两幅图像分别扩展至区域图像大小，扩大了的部分取原图像相应部分填充；

4）灰度校正，由于拍摄角度和曝光时间等条件的不同，拼接图像可能存在光强差异，使得拼接后的图像接缝处存在明显的明暗变化。为了实现无缝拼接，需要对图像拼接处的缝隙进行灰度校正，详细灰度校正步骤如3.2所述。

5）得到两幅图像拼接后的最终图像，本文算法下得到的图像拼接结果如图3（d）所示。

图3 图像拼接示例Fig.3 An example of image mosaic

3.2 灰度校正

光学系统中，在物方亮度均匀的情况下，轴外像点M′的照度可表示为：

根据与光轴成ω′角的像素位上照度按cos4ω′的比例减少这一规律，可以对原始图像乘以1/cos4ω′进行灰度校正。

通常光源照度中心并不严格在图像中心。因此，对于一维照度曲线，可以设 ω′=s（x-x0），其中 s为系数，x 为横向坐标，x0为横轴方向照度中心，则有：

利用非线性最小二乘估计法，按照式（10）对原图背景中x方向进行照度曲线拟合，可得到现场照度中心方向的坐标。

然后再用同样的方法对y方向的照度也进行拟合，这样就得到了现场的照度中心坐标（x0，y0），图像的二维灰度校正函数就可以表示为

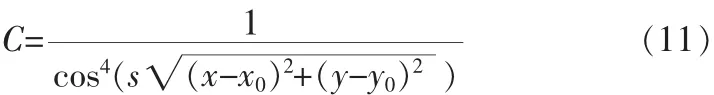
利用式（11）生成与原图尺寸相同的灰度校正曲线，并将该曲线与原图相乘即可对原图进行灰度校正。

4 结 论

本文针对目前基于SIFT的图像拼接算法复杂度较高和特征点匹配不准等问题，提出了一种基于改进SIFT的图像拼接算法。算法在SIFT特征提取过程中简化了SIFT特征描述符，降低了算法的复杂度，同时在特征匹配过程中采用模拟退火算法进行特征点匹配，降低了匹配误差。实验结果表明，本文算法在降低SIFT特征提取的同时，取得了良好的图像拼接效果。今后的工作将从进一步深入探讨SIFT特征点的稳定性以及特征点匹配精度，进一步提高算法整体性能等方面展开。

[1]Kybic J.High-dimensional mutual information estimation for image registration using control point and intensity[J].IEEE Transaction on Image，2004，13（8）：1115-1127.

[2]Zitova B，Flusser J.Image registration methods:a survey[J].Image and vision computing，2003，21（11）：977-1000.

[3]田伟刚，郭雷，黄雷.一种应用于图像配准中的点特征匹配算法[J].微电子学与计算机，2008，25（3）：172-174.TIAN Wei-gang，GUO Lei，HUANG Lei.An algorithm for point pattern matching applied to the registration of images with relatively great affine geometric distortion[J].Microelectronics&Computer，2008，25（3）：172-174.

[4]CHEN Jiun-hung，CHEN Chu-song，Chen Yong-sheng.Fast algorithm for robust template matching with M-estimators[J]．IEEE Trans on Signal Processing，2003，51（1）：230-243．

[5]CHENFu-xing，WANGRun-sheng.Fast RANSACwith preview model parameters evaluation[J]．Journal of Software，2006，16（8）：1431-1437．

[6]Kasar T，Ramakrishnaa A G．Block-based feature detection and matching for mosaicing of camera-captured document images[C]//Proc of IEEE Region 10 Conference，Symposium on Applications of Holography in Mechanics，New York:ASME，2007：1-4.

[7]邹北骥，阮鹏，向遥.一种精确匹配的全景图自动拼接算法[J].计算机工程与科学，2010，32（8）:60-63.ZOU Bei-ji，RUAN Peng，XIANG Yao.An automatic panoramic images mosaic algorithm with precise matching[J].Computer Engineering&Science，2010，32（8）：60-63.

[8]FANG Xian-yong，ZHANG Ming-min，PAN Zhi-geng，et al.A new method of manifold mosaic for large displacement images[J].Journal of Computer Science and Technology，2006，21（2）：218-223．

[9]Lowe D.Distinctive image features from scale invariant keypoints[J].International Journal of Computer Vision，2004，60（2）:91-110.

[10]兰世爽，孙劲光.基于改进SIFT的抗几何攻击的数字水印[J].计算机工程与应用，2011，49（7）:200-203.LAN Shi-shuang，SUN Jin-guang.Geometrical attack digital watermarkingbased onimproved SIFT[J].Computer Engineering and Applications，2011，49（7）：200-203.

[11]金聪，叶俊民，许凯华，等.具有抗几何攻击能力的盲数字图像水印算法[J].计算机学报，2007，30（3）：474-482.JINCong，YEJun-Min，XUKai-hua.Blind image watermarking algorithm resist to geometrical attacks[J].Chinese Journal of Computers，2007，30（3）：474-482.