土壤气相抽提过程中多孔介质扰动的数值分析

范 伟,章光新*,路 莹,杨悦锁,3,董李勤

(1.中国科学院东北地理与农业生态研究所,中国科学院湿地生态与环境重点实验室,吉林 长春 130012；2.吉林大学环境与资源学院,吉林 长春 130026；3.卡迪夫大学地球与海洋科学学院,英国 卡迪夫 CF 103YE)

全球工业化进程中的场地污染问题近年不断凸显、引发了各种环境风险与安全隐患,场地污染修复因而成为全社会关注的热点,污染修复理论、方法与技术的研究作为污染防治工作的科技支撑,是当前环境领域重点关注的课题[1-2].与以往的修复研究聚焦于地下环境条件、污染物性质与系统运行特征对修复过程及机制的影响相比[3-4],近年来一些研究开始关注场地人为修复活动对外部环境的“反作用”,即探讨修复过程可能引起的地下环境物理、化学与生物变化,例如注气修复带来的地下水水丘与侧向迁移[5]、强化生物修复引起的水化学[6]及微生物群落响应[7]等,这些变化会对场地修复过程产生反馈.

土壤气相抽提(SVE)是当前全球广泛使用的土壤与地下水污染高效修复技术之一[8],主要利用真空设备产生负压梯度、驱使一定地下区域内(抽提影响带)的空气在孔隙通道中运移,携带挥发性污染组分流向抽提系统,最后在地面进行收集处理[9].已有研究集中于对比分析土壤介质、污染组分、系统运行参数等因素对SVE过程及其修复效果的影响,揭示了环境特征与系统调控影响下的SVE特征和机理[4,10].作者前期研究发现,在室内及实际污染场地的Air Sparging-SVE联合修复中,还可观测到地下多孔介质颗粒在气流扰动驱替作用下发生迁移,多孔介质的孔隙结构与渗透性均发生改变[11],这一现象与 Kong等[12]的室内观测一致.考虑到多孔介质的颗粒配级、渗透性及非均匀性等与抽提影响带的气体流型、气-液相间接触以及污染修复过程密切相关[4,13],刻画抽提过程对多孔介质的扰动成为SVE机理研究及工程设计不可忽视的关键问题.基于此,本文从理论机理方面开展土壤气相抽提过程中多孔介质扰动的数值分析,为上述有关问题的定量化研究奠定基础.

1 材料与方法

1.1 SVE流动过程理论模型

1.1.1 SVE水气二相流动的连续性方程 假定流体不可压缩,流动过程符合达西定律.在 SVE影响带内土壤水-抽提气流二相流动区选取典型单元体,则根据质量守恒定律在Δt内流入与流出单元体的流体质量差应与其内流体的变化量相等：

式中：mx、my、mz分别为通过各向单位面积的质量;vi为渗流速度;iρ为i相流体密度;φ为单元体孔隙度;Si为i相饱和度.

根据连续介质流体动力学理论,i相的孔隙流速可用Darcy定律表示为：

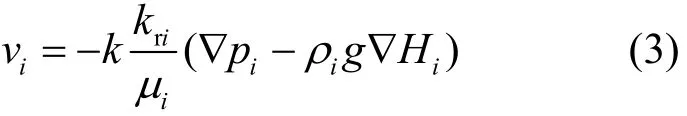
式中：k为介质固有渗透率;kri为i相的相对渗透率;iμ为i相动力黏滞系数;pi为i相的压力;g为重力加速度;∇Hi为i相压力头差.

将渗流速度的 Darcy表达式代入式(2)得到任意i相流体(水/气)的渗流连续性方程：

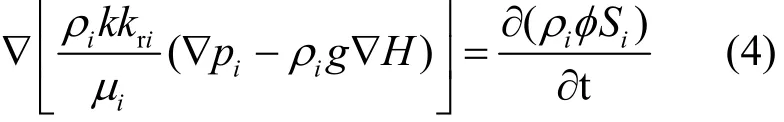
1.1.2 模型变量及其耦合关系 对式(4)中的变量进行定义,并构建不同变量之间的耦合关系[14-15]如下：

式中：Sw,Sg分别为水相和气相的饱和度;Pg,Pw分别为气相和水相的压力;m为 van Genuchten-Mualem 模型常量.由式(4)～式(8)共同组成 SVE二相流动过程模型,联立可实现SVE过程中饱和度、压力场及速度场的求解.

1.2 多孔介质扰动及其定量表征

对于 SVE影响带内体积为Ve的典型单元体,n为孔隙度,SVE运行之前单元体内初始气体及土壤水占据的体积为Vg_0、Vw_0,则初始气、水相饱和度Sg_0、Sw_0为：

式中：tφ与0φ分别为t时刻与初始状态的空隙度.由式(17)可定量识别Δt时段内的渗透率变化.

1.3 SVE过程及多孔介质扰动的概念模型

1.3.1 物理模型及参数赋值 如图1所示,构建单井SVE轴对称物理模型.在(x,y)典型垂向剖面上,包气带厚度为M,单侧宽度为L,地下水面设置为y=0平面,SVE井抽提段在(0,l1)～(0,l2)之间.

图1 场地SVE示意Fig.1 Definition sketch of the SVE physical system

场地相关的模型参数如下表所示：

1.3.2 模型定解条件 模型的定解条件包括初始条件及边界条件两部分：

初始条件

t=0时,空间各处均为二相等势体,水相压力为 ：pw_0=pa+ 5[m]·ρg· g-ρw·g ·y;气 相 压 力为：pg_0=pa+ρg·(5 [ m]-y)·g .

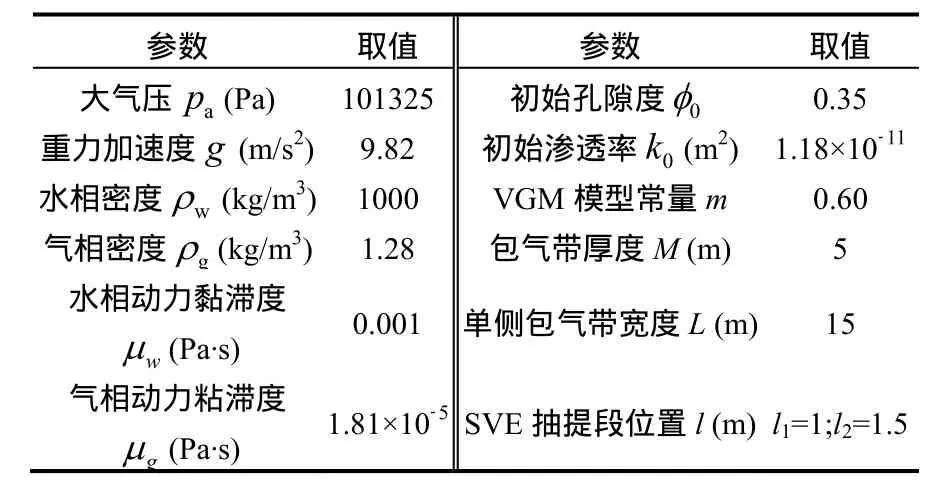
表1 模型常量参数赋值表[11,19]Table 1 Summary of physical characteristics in field SVE experiment

边界条件

其中,Γ1为一类边界,Γ2为二类边界.

2 数值模拟及结果分析

上述数学模型的有限元三角剖分、边界条件和初始条件输入以及偏微分方程的求解均通过Femlab实现.考虑到实际应用中一般SVE抽提真空度 Δp=pa-ps在 10～30kPa之间,故本次分别模拟SVE抽提段压力为0.7×105Pa和0.9×105Pa的两种压力情景(相应的真空度Δp约为 31kPa和 11kPa).参数C与介质特性有关,且由(16)式可知函数 Δφ=f(C)的一阶导数大于 0,本次选取C=0.1、0.3、0.5、0.8不同取值时的4种模拟情景进行对比分析.

2.1 气相压力场及速度场分布

通过二相流动模拟分析可获取稳定状态下模拟区压力场及速度场的空间分布(图 2).结果显示：越接近 SVE抽提段,空间各处气相的真空度、压力梯度及气流速度均越大,以有效真空度为 0.1kPa 为界线,ps=0.7×105Pa(Δp=31kPa)时抽提有效覆盖半径达到9m,ps=0.9×105Pa(Δp=11kPa)时则减小至 8.5m,可知抽提真空度大的条件下SVE影响半径也较大,在半径小于6m范围内,气流速度可达到 0.0001m/s.进一步模拟计算稳态条件下的气相饱和度,如图中短划曲线所示,包气带部分区域出现Sg=0,即抽提作用下地下水位出现一定的抬升,但在两种压力情景下抬升的幅度差异并不明显,短划曲线Sg=0几乎重合.

图2 稳态不同情境下的气相真空度与速度场分布Fig.2 Spatial distribution of air vaccum and velocity at steady stage of SVE

2.2 特定压力及C值情景下孔隙度及渗透率随时间的动态变化

在ps=0.7×105Pa、C=0.8情景下,对上述数学模型进行瞬态模拟分析.选取模拟区内与抽提段距离递增的4个典型点P1(1,1),P2(1.5,1.5), P3(2,2),P4(3,3),则模型求解可分别得到任意时刻各点的孔隙度变幅,并根据孔隙度～渗透率关系得到渗透率随时间的动态变化.结果如图 3所示：SVE过程中孔隙度及渗透率随时间呈现先增加后稳定的动态变化,包气带介质整体达到稳定所需的时长约为 60min;与抽提段距离越近,孔隙度及渗透率变化响应越快、达到平稳所需的时间也越短,增幅越大,如P1点在约40min后达到稳定、孔隙度增幅为0.0387,P4点约在60min后达到稳定、孔隙度增幅为0.0031,相应地,P1和P4点介质渗透率分别增加至 2.22×10-11m2和 1.25×10-11m2.

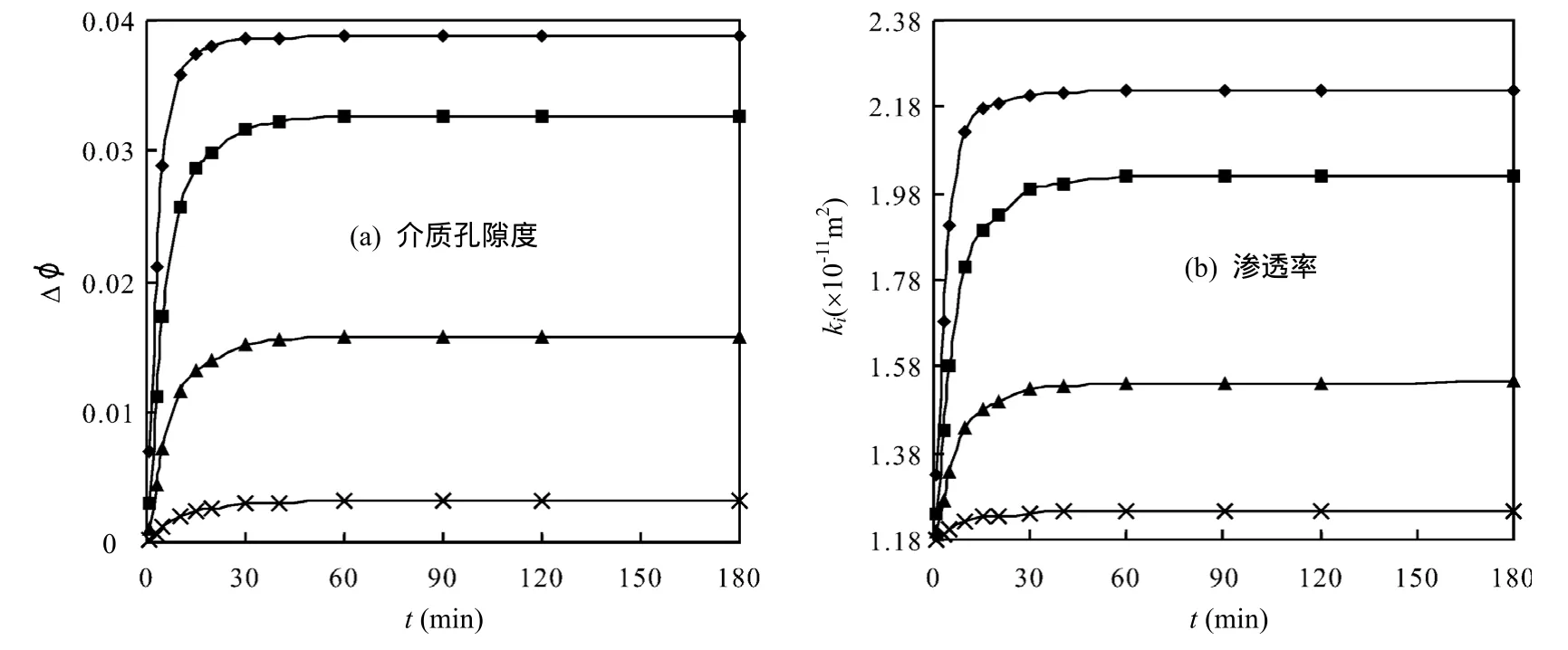
图3 SVE过程典型点介质孔隙度及渗透率随时间动态变化Fig.3 Temporal trends of porosity and permeability at four spatial points during SVE

2.3 不同压力情景参数C不同取值条件下的孔隙度变化

基于上述不同压力情景的模拟分析,结合多孔介质扰动的定量表征,得到参数C不同取值条件下稳定后的孔隙度变化,如图4所示.离SVE抽提段越近,介质孔隙度变化越大.相同抽提压力下,伴随着C值的增加,空间同一位置的孔隙度变幅逐渐增大,ps=0.9×105Pa时,Δφ=0.005分布界线的横向最大距离在C=0.1,0.3,0.5,0.8时分别为1.36,4.04,5.34,6.75m,且C=0.1和 0.8时的最大Δφ分别约为 0.009和 0.055,即影响范围及程度随着C的增加而增大;对比相同C值条件下(C=0.8),不同 SVE 抽提压力情景(ps=0.9,0.7×105Pa),可知形成真空度越大的条件下(抽提压力0.7×105Pa)孔隙度增幅越大,Δφ=0.005分布界线的横向最大距离增加至 7.24m,最大Δφ则达到0.066.综上所述,孔隙度增幅与抽提真空度和参数C取值呈正相关.

3 结论

3.1 对于特定的场地,SVE影响带的空间形态与抽提真空度密切相关,抽提真空度越大,影响半径越大.就本模拟场地而言,SVE抽提段真空度为11kPa和31kPa的2种压力情景下,其影响半径分别约为8.5和9.0m;

3.2 SVE过程中多孔介质的孔隙度及渗透率呈现显著的时空动态,二者随时间呈现先增加后稳定的变化规律,达到稳定所需的时长及其变化幅度则与离抽提段的空间距离成反相关,距离抽提段较近的 P1点在约40min后达到稳定、孔隙度增幅为 0.0387,较远的P4点约在60min后达到稳定、孔隙度增幅为 0.0031,相应地,P1和 P4点介质渗透率分别从 1.18×10-11m2增加至 2.22×10-11、1.25×10-11m2;

3.3 在相同抽提压力下,孔隙度增幅与关键参数C值成正相关,抽提压力为 0.9×105Pa条件下,C=0.1和 0.8时的孔隙度最大增幅分别约为0.009和 0.055;相同参数C条件下,孔隙度增幅与抽提压力成正相关,C=0.8条件下,抽提压力为 0.7×105Pa时的孔隙度最大增幅则达到0.066.

图4 不同抽提压力及C取值条件下的孔隙度增幅空间分布Fig.4 Comparisons of changes in porosity under different SVE settings

[1] Reddy K R. Technical Challenges to in-situ remediation of polluted sites [J]. Geotechnical and Geological Engineering,2010,28(3)：211-221.

[2] 骆永明.中国污染场地修复的研究进展、问题与展望 [J]. 环境监测管理与技术, 2011,23(3)：1-6.

[3] Rogers S W, Ong S K. Inflence of porous media, airflow rate, and air channel spacing on benzene NAPL removal during air sparging [J]. Environmental Science and Technology, 2000,34(5)：764-770.

[4] Qin C Y, Zhao Y S, Zheng W, et al. Study on influencing factors on removal of chlorobenzene from unsaturated zone by soil vapor extraction [J]. Journal of Hazardous Materials, 2010,176(1-3)：294-299.

[5] 范 伟,杨悦锁,路 莹,等.层间地下水污染曝气修复的影响带[J]. 化工学报, 2011,62(9)：2600-2607.

[6] Davis G B, Patterson B M, Johnston C D. Aerobic bioremediation of 1, 2 dichloroethane and vinyl chloride at field scale [J]. Journal of Contaminant Hydrology, 2009, 107(1-2)：91-100.

[7] Kao C M, Chen C Y, Chen S C, et al. Application of insitu biosparging to remediate a petroleum-hydrocarbon spill site： Field and microbial evaluation [J]. Chemosphere, 2008,70(8)：1492-1499.

[8] Soares A A, Pinho M T, Albergaria J T, et al. Sequential application of soil vapor extraction and bioremediation processes for the remediation of ethylbenzene-contaminated soils [J]. Water,Air, and Soil Pollution, 2012, DOI： 10.1007/s11270-011-1051-y.

[9] Høier C K, Sonnenborg T O, Jensen K H, et al. Model analysis of mechanisms controlling pneumatic soil vapor extraction [J].Journal of Contaminant Hydrology, 2009,103(3-4)：82-98.

[10] Albergaria J T, Alvim-Ferrza M da C, Delerue-Matos C. Soil vapor extraction in sandy soils： Influence of airflow rate [J].Chemosphere, 2008,73(9)：1557-1561.

[11] 范 伟.石油类污染场地地下水原位空气扰动修复研究 [D].长春：吉林大学, 2011.

[12] Kong X Z, Kinzelbach W, Stauffer F. Migration of air channels：an instability of air flow in mobile saturated porous media [J].Chemical Engineering Science, 2009,64(7)：1528-1535.

[13] Gidda T, Stiver W H, Zytner R G. Measuring aqueous-air and sorbed-aqueous mass transfer coefficients for application in soil vapor extraction [J]. Journal of Environmental Engineering,2011,137(10)：880-888.

[14] Hoeg S, Schöler H F, Warnatz J. Assessment of interfacial mass transfer in water-unsaturated soils during vapor extraction [J].Journal of Contaminant Hydrology, 2004,74(1-4)：163-195.

[15] 薛 强,冯夏庭,梁 冰,等.水气二相流系统的 K-S-P模型参数反演的最优估计 [J]. 水科学进展, 2005,16(4)：488- 493.

[16] El-Farhan Y H, Denovio N M, Herman J S, et al. Mobilization and transport of soil particles during infiltration experiments in an agricultural field, Shenandoah Valley, Virginia [J]. Environmental Science and Technology, 2000,34(17)：3555-3559.

[17] Tsai Y J. Air distribution and size changes in the remediated zone after air sparging for soil particle movement [J]. Journal of Hazardous Materials, 2008,158(2/3)：438-444.

[18] 路 莹.北京平谷地区雨洪水地下回灌堵塞机理分析与模拟研究 [D]. 长春：吉林大学, 2009.

[19] Leij F J, Russell W B, Lesch S M. Closed-form expressions for water retention and conductivity data [J]. Ground Water, 1997,35(5)：848-858.