天津市轨道交通网络化运营票务清分中的路径确定方法探讨＊

于 航 徐道强

（1.天津理工大学自动化学院，300222，天津；2.天津市地下铁道运营公司，300222，天津∥第一作者，讲师）

1 清分方法的研究背景

天津市轨道交通目前规划共有13条线路，随着新线的建成和运营筹备工作的深入，对无障碍换乘情况下的多线路之间票务收入的清分，成为网络化运营需要解决的一个重要问题。

轨道交通网络化运营情况下的清分方法，可以人为的分为精确法和近似法两类。由于轨道交通线网内每一个乘客的具体乘车路径很难精确得到，因此精确法需要增加建设投资和维护成本，可操作性很低；近似方法对乘客实际乘车路径做近似处理，可以兼顾可操作性和公平合理性。

目前的轨道交通清分方法多属于近似方法。“最短路径法”是一种使用较多的典型近似法，即：在路网中任意两个车站之间找出一条确定的最短路径，然后按照各运营线路在此最短路径中所占的比例对每笔换乘交易的票款收益进行清分，即称为最短路径方法。作为一种经典的寻径方案，最短路径算法已经得到广泛的应用。然而在很多实际环境中，最短路径并不一定是首选的路径。在城市轨道交通或公路交通中，由于路网中理论上的最短路径舒适度不够或比较拥挤，旅客或车辆往往会出于方便及节省时间的目的而实际选择了其他的径路。这就说明，为了解决某些实际问题，有时必须兼顾网络中其他的优选路径。

在轨道交通网络中，确定路径时必须首先确定优选的准则。乘客在乘坐轨道交通出行时往往会选择运营里程最短、换乘总时间最少或换乘站点个数最少的线路。目前影响乘客选择出行径路的因素主要有线路运营里程；乘轨道交通出行的总时间；换乘站点数；换乘步行距离或换乘所需时间；新路服务水平（运营服务时间、行车时间、行车间隔）等。因此，在优选换乘路径的过程中可以以运营里程最短、换乘时间最短或换乘站点数最少作为寻径的标准。此外，考虑到客流分布的概率，还可以在上述标准的基础上，通过影响条件的不同组合来确定更逼近实际情况的寻径方案。

这里需要特别说明的是，不管采用何种清分方法，都只能实现相对的合理和公平。

2 清分原则

清分的实质是计算线网中各条线路（参与服务的线路）的经济贡献。而体现各条线路经济贡献的因素有很多，如建设投资成本、路网的具体属性、运营服务水平、客流量（包括换乘）及行车时间、行车间隔等。在这些主要因素中，建设投资成本主要体现为投资贡献，属于短期因素；其他各类规则则主要体现运营贡献，属于长期因素。因此按运营贡献清分更为合理，更为有效。

在线网的各种属性中，里程、站数、换乘站、换乘便捷性等这些重要属性可变程度低，可视为静态属性；而体现运营服务水平的行车间隔、站间行车时间、运营服务时间等属性可变程度高，可视为动态属性。

从运营贡献的角度来看，票务收入的运营贡献已几乎完全包含了客流量的贡献。按运营贡献对线网票务收入清分时，必须与体现路网结构的静态属性和体现运营服务水平的动态属性结合。

因此，结合以上分析，轨道交通系统线网票务收入的清分原则应为：满足线网的发展趋势，适应路网规划要求；满足票价规定的调整要求；按线路或按运营商清分；体现清分的权重和路网重要属性的相关性；体现清分的权重与运营服务水平的相关性。

3 网络化运营中清分规则的应用

以轨道交通路网结构为基础的清分算法，应该建立在严格的数学模型之上，通用灵活，高效快捷，能够生成一套科学、规则、合理的票务清分规则表；依据清分规则表，清分中心及时、公平地进行票务清分，使清分业者对象能够获得其应该获取的票款份额。

在轨道交通长远规划中，天津城市轨道交通将建成13条线路，这要求清分规则算法在满足现有路网清分要求的同时，必须考虑到增加线路、车站后算法结果是否能符合清分业者对象的利益，因此清分算法模型应具有很强的通用性、合理性、灵活性和扩展性等特点。

在清分算法模型中确定乘车路径是关键，现在确定乘车路径的算法主要有最短路径法和多路径法。在以最短路径的清分算法中只考虑到路径这一关键要素，而实际上时间、换乘车站间步行距离、线路和车站的拥挤情况等都可能成为乘客决定其乘车路线的因素，所以单纯以乘车里程数为要素的最短路径法不符合清分算法模型的合理性及灵活性。多路径法是指路网中任意两个车站之间每条可能的路径都确定一个被乘客选择的概率，在确定参与票款计算的合理选择路径后，按照确定的公式计算各运营线路的各自收益。多路径法充分考虑影响乘客确定乘车路径的各要素，确定一到多条的乘车路径进行清分，这既接近乘客乘车路线的实际选择，也符合运营公司的利益。因此在天津轨道交通路网寻径方案确定时，以多路径法作为确定乘车路径算法。

清分算法模型考虑到通用性以及今后的扩展性，算法模型中的各个算式可以由各运营公司共同设计调整，模型将根据设计出的算式计算各路径上线路的票款分配比例。当某种乘车要素的影响力足够大到能够决定乘客乘车路线的选择并最终涉及到票款分配时，清分算法能够在不修改其算法模型结构的基础上加入此要素，得到合理的清分规则。

以下内容中提及的一些名词解释如下：①线路——指轨道交通路网拓扑图中被标示为不同的线路，并隶属于不同的运营公司；②路径——从站点1出发，到达站点2的路线，因为轨道交通的网状拓扑，存在1站到2站的多条路径；③路段——对于跨越多条线路的换乘路径，是以实际换乘点为断点的线段组成，而每条线段属于且仅属于一条线路，此线段即为路段；④遍历——遍历是指沿着某条搜索路线，依次对网络中每个点均做一次且仅做一次访问，如图1遍历图示；⑤换乘次数——遍历路网拓扑时经过换乘点且发生实际换乘的最大换乘次数。

图1 遍历图示

根据目前的天津轨道交通路网规划建立整个路网模型，以后可根据实际路网建设情况进行部分调整。这种方法可以评估清分模型算法在处理整个路网时的性能，避免设计风险以及未来修改模型所带来的风险。

4 清分算法寻径方案模型的建立

4.1 寻径模型的建立——遍历操作

遍历的目的是找出在轨道交通路网拓扑中一对进站和出站之间可能的路径。因为在网状拓扑图中，换乘车站即是两条线路的交叉点，三个换乘站可能形成环路，所以为避免在遍历时算法线路无穷的循环，需要控制从一条线路换乘到另条线路的次数，即换乘次数控制。对于乘客，一般不会选择超过3次以上的换乘的乘车路径，最终遍历结果得到在换乘次数控制下的一对进站和出站之间所有可能的路径。

遍历结果的数据量取决于车站与线路的数量，并随着线路和车站的增长呈比例增长。根据天津市轨道交通规划的长远目标，最终将有13条线路，338个车站，24个换乘站，因此任意两个可达车站的数量为C2338＝338×（338－1）／2＝56 953（对）。

但对于同条线路的车站，认为乘客是不换乘的，考虑到13条线路，338个车站，平均每条线路26个车站，则不经过换乘的进站和出站为C226＝26×（26－1）／2×13＝4 225（对）。

所以需通过换乘才能到达的车站对大概有52 728对。考虑到换乘次数的控制，则换乘遍历结果的可能路径数目

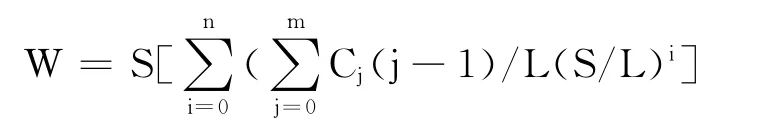
式中：

W——在换乘次数控制下所有换乘路径数目；

S——路网中车站站点总数；

Cj——路网中j条线相交换乘站点总数；

L——路网中线路总数；

n——系统定义的最多换乘次数；

m——路网中相交于同一站点的最多线路条数。

路网结构中2条路线相交的换乘节点23个，3线相交的换乘节点数为1个，且系统定义最大换乘次数为3。路网结构中有13条线路，338个车站，平均每条线路近似有26个车站。假定平均每条线路有换乘车站约为2个，则依据公式，所有换乘路径有338×（26＋2×（26＋2×（26＋2×26））＝131 820（条）。考虑到实际的路网结构中可能有4条线相交一个换乘点的情况，所以路径条数还会有所增长。

4.2 各种特殊路网拓扑的处理方法

4.2.1 交叉线

在路网拓扑结构中存在多条线路在一个换乘点交汇的情况，在遍历算法中是以深度优先遍历的。在遍历完一条线路所有车站后将退回到上一换乘点，再遍历该换乘点上另条线路的站点（如图2交叉线路径遍历所示）。

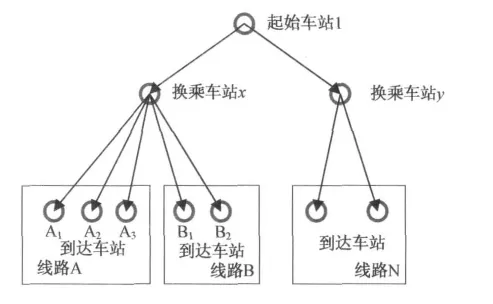
图2 交叉线路径遍历

在遍历算法中，从起始站点1出发的遍历过程如下：1→x，判断x点是否是换乘点；遍历经过x换乘点的线路；遍历该线路所属车站中无换乘点，记录所有遍历的到达车站；退回x换乘点，检查是否还有其他线路经过x点，如果有跳转到3，否则退回到上一换乘点，直到退回到起始站点，结束本起始站点的遍历。

4.2.2 环线

在路网拓扑结构中某条线路成为封闭的环。在遍历算法中的一个重要特点是无向性，只记录起点车站、换乘车站、到达车站，而不记录在该条路径上经过每个车站以及站点顺序，但在权值计算时需要考虑到路径里程和时间的不同。

以图3路网示意图为例，从A1车站进站，B1车站出站，在乘客选择乘车路径时可能的有：路径一——A1→A2→A3→B1；路径二——A1→An→A4→A3→B1；路径三——A1→An→BnA3→B1；

在这里讨论路径一和路径二，在遍历算法中记录的是两个路段：A1→A3、A3→B1，所以对遍历算法而言，这两条路径其实是一条。

4.2.3 共线

在路网拓扑结构中有2条线路甚至多条线路的部分共线重叠的情况，该共线上的车站同属于2条或多条线路。

在遍历算法剔除掉不合理路径的过程中，首先删除起始站点与到达站点在同一条线路的，因此在共线以外共线线路站点出发、在共线范围内出站的票款应属于该线路；如果使用了共线车站其他线路的出站闸机，因为闸机所属线路提供了服务，可以酌情收取相应手续费。对于在共线内车站出发，共线线路车站出站的情况也可做同样处理。对于共线车站进站（出站）、在共线外线路车站出站（进站）的，以及换乘经过共线范围的，共线路段应由共线线路按比例清分此份票款收益。

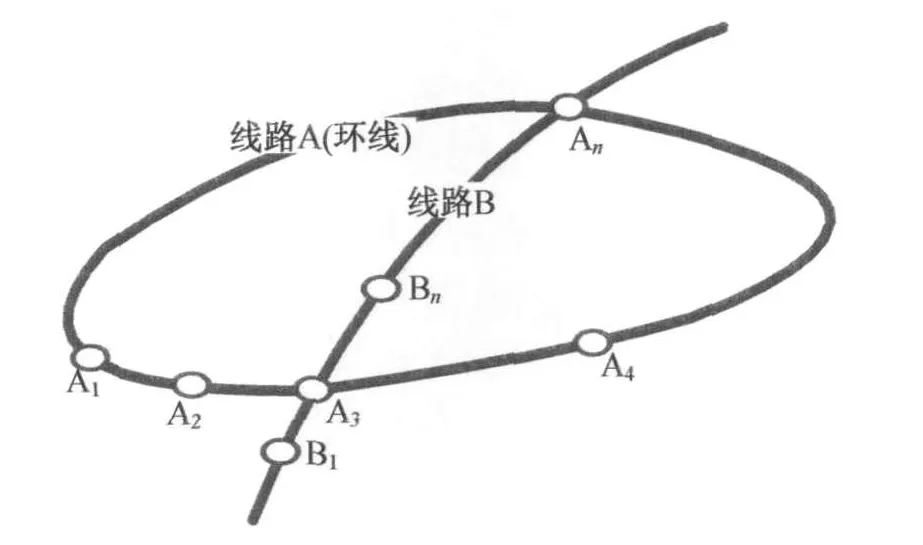
图3 路网示意图

5 天津轨道交通路网路径确定方法简析

天津轨道交通目前有4条线路，呈交叉网状结构，有3个换乘站，其中1个换乘站为1条线路的起止站点。未来规划的路网呈交叉网状放射结构，即包涵交叉线路及环形交叉线路，路网覆盖面较广，两站之间可乘客选择的路径较多，清分算法较为复杂。

在清分模型建立过程中，应用遍历算法计算出路网中任意两站之间的所有换乘路径，但是由于路网中影响乘客出行的因素较多，遍历方法算出的有些路径乘客的选择概率可能是零，因此天津轨道交通路网清分模型在路径选择时采用了多因素修订综合优选的方法，对遍历路径进行甄选。将影响乘客换乘选择的权重因素作为因子，如乘车时间、换乘时间、舒适度、换乘次数等，在因子作用下，利用模型计算出各遍历路径的换乘概率，然后由各受益方共同决策确定可接受的路径选择概率值，最后按照每条被选线路各运营商提供的服务计算出票款的清分比例。

在模型建立过程中，甄选所有遍历路径中参与票款清分计算的有效路径是优化清分寻径方案的关键。在这个方面考虑了以下几个限制条件：①有效路径倍增限制值，超过最短有效路径因子n倍的路径，则放弃该路径；②有效路径增长限制值，超过最短有效路径因子一定数量m的路径，则放弃该路径；③有效路径最大数量，限制每次寻径时最多的有效路径，其余舍弃。通过以上几个限制条件将参与票款清分计算的有效路径减到合理的范围。

6 结语

寻径方案模型的建立是清分算法模型必不可少的一部分，是清分清算的前提。选择路网遍历操作加多因素综合优选法是众多寻径模型中的一种，具有高效、准确的寻径特点，能为清分清算提供有效的乘客动向依据。以上内容对于庞大且复杂的清分算法模型只是冰山一角。每个城市的交通路网都有其特殊性，因此轨道交通寻径模型、清分算法模型必须以当前轨道交通路网为基础来建立。

天津轨道交通清分方法的确定还在探索和研究阶段。在轨道交通网络化大趋势面前，确定轨道交通清分规则和建立清分模型，是公平、公正、合理的服务票款收入清分公正的前提和基础。在清分规则和清分模型确立之后，再根据乘客出行习惯和具体问卷调查的方式，对清分规则进行修订，以期达到更精确、更公平的清分结果。

［1］ 吕利民，黎卓明.城市轨道交通乘客换乘路径分配比例算法［J］.地铁科技.2006，（3）：7.

［2］ 朱沪生.上海城市轨道交通清分系统的建设［J］.都市快轨交通.2006，19（5）：12.

［3］ 毛保华，四兵锋.城市轨道交通网络管理及收入分配理论方法［M］.北京：科学出版社.2007.

［4］ 上海申通轨道交通研究咨询有限公司.城市轨道交通网络化探索和实践［M］.北京：人民出版社.2010.

［5］ 闫彬.城市轨道交通自动售检票系统研析［J］.铁路通信信号工程技术，2004（2）：32.

［6］ 范巍.城市轨道交通自动售检票中央清分系统概论［J］.铁路通信信号工程技术，2004（2）：37.

［7］ 孙波，邱继红，孙泽俊.动态规划在轨道交通清分系统中的应用［J］.城市轨道交通研究，2011（8）：54.