基于宾汉姆流体的海底隧道穿越裂隙岩体注浆扩散半径计算

汪 磊,李 涛

(1.上海工程技术大学城轨学院,上海 201620;2.北京交通大学土建学院,北京 100044)

注浆技术自从发明以来，已经广泛地应用于封堵涌水和改良地层，在基础建设的各个方面起到了良好的作用[1]。而在海底隧道的修建中，由于环境的特殊性，裂隙岩体和无限量的海水补给使得隧道的安全施工更加特殊，隧道突涌水破坏或围岩失稳都会带来不可以挽回的后果，因此对于不良地质段隧道的施工往往采用预注浆对围岩进行超前加固，但目前预注浆加固过程中浆液扩散范围确定困难，同时由于注浆时地质情况复杂，计算参数选取困难等原因，无法得出较为合理的计算结果，继而导致了一些注浆方案无法确定[2-3]。本文以青岛胶州湾海底隧道预注浆加固工程为背景，针对海底不良地质段隧道注浆扩散半径进行计算，分别考虑基于宾汉姆流体的注浆扩散半径进行计算，通过分析各种因素和他们的变化规律，得出海底隧道的较为合理的注浆扩散半径。

1 工程概况

青岛胶州湾海底隧道是我国大陆第二条海底隧道，隧道南接黄岛区的薛家岛，北连青岛团岛，下穿胶州湾湾口海域，隧道全长6 170 m，其中海域段长3 950 m。隧道采用双向双洞6车道，中间设服务隧道，隧道主要采用钻爆法施工。根据前期工程地质勘探的结果，隧道海域段基岩受构造运动影响较严重，破碎岩体及抗风化能力较低的辉绿岩脉较发育，对水敏感的Ⅳ～Ⅴ级围岩所占比例较大，其中，隧道主洞Ⅱ～Ⅲ级围岩约占55.7%，Ⅳ级围岩约占38.1%，Ⅴ级围岩约占6.2%隧道顶部25 m内岩体中的地下水活动痕迹普遍较明显，隧道开挖时的爆破震动和围岩松弛都可能使其透水性加剧，埋深不足25 m的海域段占了相当大的比例。

2 胶州湾海底隧道预注浆方案

根据《胶州湾隧道超前预注浆堵水方案和技术、设备及施工突发涌水情况下应急预案及防治技术研究》现场注浆实施方案及《青岛胶州湾隧道工程地质报告》，可以得出隧道围岩渗透性和孔隙特征和浆液配比参数和注浆加固参数，分别如表1、表2和表3所示。

表1 胶州湾海底隧道围岩渗透和孔隙特性参数

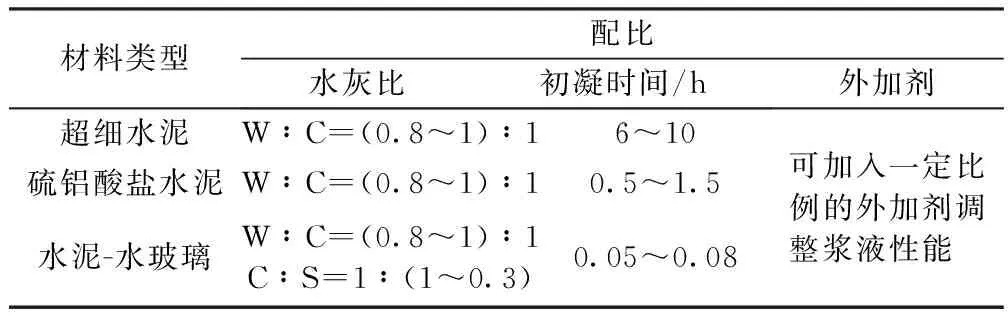
表2 浆液配比参数[2]

表3 胶州湾海底隧道预注浆参数[2]

以下将根据胶州湾海底隧道的注浆方案相关参数，计算断层破碎带裂隙岩体的注浆扩散半径，评估注浆设计是否满足围岩加固的要求。

3 宾汉姆流体注浆扩散规律分析

3.1 浆液特性分析

地下水在地层中流动时，按其流线形态可分为层流和紊流2种。一般情况，浆液在地层中的运动规律和地下水的运动规律非常相似，不同之处是浆液具有黏度，不像水那样容易流动[4]。浆液的流变性反应浆液在外力作用的流动性，浆液的流动性越好，浆液流动过程中压力损失越小，浆液在岩土介质中扩散的就越远；反之，浆液流动过程中压力损失大，浆液就不易扩散。

纯水泥浆的流型随水灰比不同可分为3种。低水灰比(W/C=0.5～0.7)的水泥浆为幂律流体；中水灰比(W/C=0.8～1.0)的为宾汉姆流体；高水灰比(W/C> 2.0)的为牛顿流体[5]。水泥黏土浆液、水泥复合浆液、聚合物水泥浆等水泥基浆液一般为宾汉姆流体，但当聚合物黏度很大使浆液黏度很大时，浆液为幂律流体[6]。随着水灰比的增大，纯水泥浆逐渐趋近于牛顿流体。水泥浆由幂律流体转化为宾汉姆流体的临界水灰比是0.7，由宾汉姆流体转化为牛顿流体的临界水灰比为1.0[7]。

根据以上的规律，由于超细水泥单液浆由极细的水泥颗粒组成，其平均粒径为4 mm，比表面积在8 000 cm2/g以上，这一性质使得超细水泥浆液有很好的可注性，其可注性与化学浆液相似，故可以按牛顿流体来考虑。水泥—水玻璃双液浆中结石体的抗压强度主要受水泥的含量控制，可用于裂隙宽度为0.2 mm以上的裂隙岩体或粒径为1 mm以上的砂层，并且水灰比为W/C=(0.8～1)∶1，所以可将其按宾汉姆流体来考虑。对于一般悬浊液如水泥浆、水泥黏土浆、水泥砂浆等都可以认为是宾汉姆流体。因此，可认为胶州湾海底隧道注浆工程中用到的超细水泥单液浆、硫铝酸水泥单液浆和水泥-水玻璃双液浆为宾汉姆流体。

3.2 裂隙岩体注浆扩散半径公式

鉴于胶州湾海底隧道注浆工程中用到的浆液可视为宾汉姆流体，宾汉姆流体在裂隙岩体中的扩散半径计算主要采用Wittke和Wallner公式与 Lombadi公式，但现有的注浆公式只限于单一裂隙或一组裂隙内浆液的流动，而黄春华公式是考虑了浆液流变性的基础之上推导出来的。

(1)Wittke和Wallner公式[8-9]

在二维平面等厚光滑裂隙中，宾汉姆浆液在注浆压力作用下产生径向流动。Wittke和Wallner根据浆液平衡方程和边界条件，可得浆液的最终扩散半径

(1)

式中，R为浆液的最终扩散半径；p0为注浆孔内的注浆压力；τ0为浆液的屈服强度；δ为裂隙宽度；r0为注浆孔半径。

(2)Lombadi公式[8-9]

对宽为δ的裂缝，Lombadi推导出浆液的最大扩散半径Rmax为

(2)

式中，Rmax为浆液的最大扩散半径；pmax为最大的注浆压力；τ0为浆液的剪切强度；δ为裂缝宽度。

(3)黄春华公式[10-11]

黄春华对裂隙灌浆中宾汉姆流体的扩散能力进行了研究，建立了考虑浆液流变特性的裂隙岩体的注浆扩散模型。假设裂隙灌浆为稳定的宾汉姆流体流动，它们在平面径向等厚裂隙的运动为低雷诺数的层流，不计惯性力和重力作用，可推导出浆液扩散半径的计算公式为

(3)

其中，

(4)

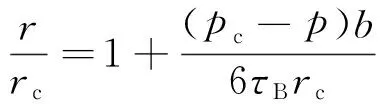
(5)

式中，pc为注浆孔裂隙处的注浆压力；p为半径r处的浆液压力；rc为灌浆孔半径；r为浆液扩散半径；τB为宾汉姆流体的剪切屈服强度；η为宾汉姆流体的塑性黏滞系数；t为注浆时间。参数ξ可以通过文献[5]表3查到。

3.3 宾汉姆浆液的扩散规律分析

宾汉姆流体在计算其浆液扩散范围方面，过去以Wittke和Wallner公式以及Lombadi公式为主，近年来则以广东水利水电科学研究所黄春华推导出的能考虑浆液流变特性的裂隙岩体注浆扩散公式应用较多，但总的来说，宾汉姆浆液在扩散规律方面主要体现如下特点。

(1)注浆压力的衰减和浆液扩散距离、裂隙宽度有关[12]。离注浆孔距离越远，注浆压力越小；裂隙宽度越小，注浆压力衰减得越快。浆液的最终扩散半径与注浆孔内的注浆压力、裂隙宽度有关。注浆孔内的注浆压力越大，裂隙宽度越大，浆液的最终扩散半径就越大。

(2)宾汉姆浆液是塑性浆液，浆液的屈服强度影响注浆压力的衰减快慢和浆液的最终扩散半径。注浆压力的衰减与浆液的扩散距离呈线性关系。

(3)宾汉姆浆液的屈服强度越大，注浆压力衰减越快；浆液的屈服强度越小，浆液的最终扩散半径越大。

4 注浆扩散半径计算

青岛胶州湾海底隧道围岩加固采用硫铝酸盐水泥单液浆或水泥—水玻璃双液浆时，可认为这种浆液为宾汉姆流体。设计时浆液的屈服强度τ0取18 Pa，注浆压力、注浆时间和裂隙宽度按设计资料选取。

4.1 按Wittke和Wallner公式计算

当采用Wittke和Wallner公式计算时，若孔内裂隙面上的压力p0取该处的静水压力400 kPa，注浆孔半径r0取为5 cm，则由计算结果可得浆液最终扩散范围与裂隙宽度之间的关系如图1所示，其中浆液扩散半径的单位为cm，裂隙宽度的单位为mm。

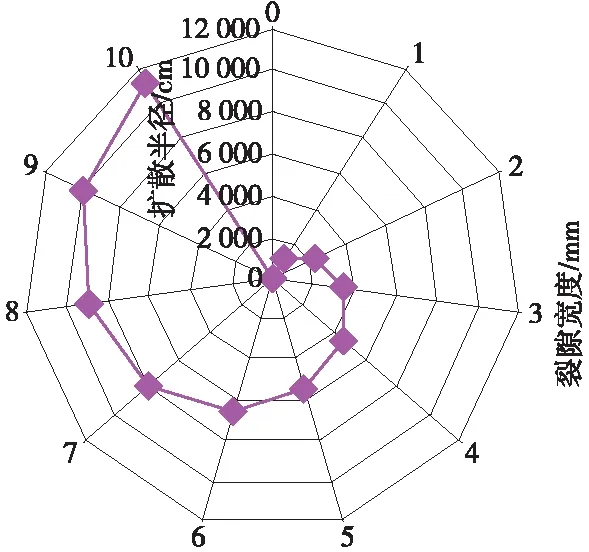
图1 浆液扩散半径与裂隙宽度关系

在公式(1)中，浆液扩散半径与裂隙宽度呈线性关系。从图1可见，当裂隙宽度为1 mm时，浆液扩散半径达到1 116 cm，已大于1.1 m，超过了注浆孔距的一半。但在实际情况下，当裂隙宽度很小时很难实现有效注浆，造成计算结果偏大的主要原因是Wittke和Wallner公式假设宾汉姆浆液在压力作用下在二维的等厚光滑裂隙中流动，即浆液在流动过程中所受的摩阻力为零。

4.2 按Lombadi公式计算

当按Lombadi公式计算时，如果最大注浆压力取3～4 MPa，裂隙宽度取0.01～10 cm，则注浆扩散半径与最大注浆压力和裂隙宽度的关系分别如图2和图3所示，图中注浆压力单位为Pa，注浆扩散半径单位为cm。

图4 浆液扩散半径与有效注浆压力关系

图2 浆液扩散半径与最大注浆压力关系

图3 浆液扩散半径与裂隙宽度关系(单位：cm)

从图2可见，对宽度为0.01 cm的裂隙，最大注浆压力即使取最小值3.0 MPa，浆液扩散半径也达到了1 666.7 cm，远大于注浆孔孔距的一半。

从图3中可以看出，在最小注浆压力3 MPa情况下，当裂隙宽度增加到3 mm时，浆液扩散半径可达500 m。

显然，Lombadi公式只考虑了最大注浆压力、裂隙宽度和浆液的屈服强度，没有考虑注浆时间、注浆岩体对浆液的摩阻力以及注浆压力在裂隙内的衰减等因素的影响，故计算结果也明显偏大。

4.3 按黄春华公式计算

黄春华公式考虑了浆液的流变特性。计算时有效注浆压力(pc-p)分别取3.0、3.5 MPa和4.0 MPa，注浆时间t分别为1 800、2 700 s和3 600 s，裂隙宽度b取0.01～10 cm，浆液的屈服强度τB取18 Pa。当(pc-p)=3.0 MPa，b=0.01 cm，τB=18 Pa，rc=5 cm，η=2.7×10-3Pa，t=3 600 s时，浆液扩散半径的计算过程如下。

(1)计算中间变量

查文献[3]中表3得ξ=4.172

(2)求浆液扩散半径

281.30 cm

类似地，可以计算各种情况下浆液的扩散半径。

图4为对应不同注浆时间的浆液扩散半径与有效注浆压力关系图，其中注浆压力单位为Pa，注浆扩散半径单位为cm。当裂隙宽度分别取0.01、0.05 cm和0.1 cm时，浆液扩散半径随着有效注浆压力的增长而增加，浆液在裂隙岩体内的渗透范围得到扩大。

图5为对应不同有效注浆压力下的浆液扩散半径与注浆时间关系图，其中注浆扩散半径单位为cm，注浆时间单位为s。当注浆压力与裂隙宽度一定时，浆液扩散半径首先随着注浆时间的增长而增加，然后逐渐趋于稳定。当裂隙宽度为0.01 cm、注浆压力为3 MPa及注浆时间为1 800 s时，浆液的扩散半径为2.813 m，大于注浆孔距的一半；而当裂隙宽度为0.1 cm、有效注浆压力为4.0 MPa及注浆时间为3 600 s时，浆液的扩散半径为36.88 m，远大于注浆孔距的一半，所以浆液扩散半径满足设计要求。

图5 浆液扩散半径与注浆时间关系

5 结论

此计算是假设浆液在一定的压力下在预设的裂隙内渗透流动造成的，它没有考虑裂隙在流体压力下的劈裂和扩张。实际上，当裂隙宽度小到一定程度或甚至没有裂隙时，在较大的注浆压力作用下，渗透注浆会变成劈裂注浆，浆液扩散半径会继续增加。对该计算结果进行分析可以得到如下结论。

(1)对于宾汉姆流体型的浆液，在设计注浆压力为3～4 MPa、注浆孔半径为5 cm和注浆时间为1 800～3 600 s时，浆液的扩散半径能满足设计要求。

(2)按宾汉姆流体计算时，浆液扩散半径在注浆开始时一般增长较快，当浆液扩散半径达到一定值后，随着注浆时间的增长，扩散半径会趋于稳定；此外，浆液扩散半径几乎与注浆压力的增长呈线性关系。但在实际地层中，浆液扩散半径不可能长时间随注浆压力呈线性增长，因为它还要受到浆液黏性变化和岩体裂隙特性的影响。

(3)在考虑浆液的流变特性时，采用黄春华公式计算得到结果的规律性与Wittke和Wallner公式和Lombadi公式的基本相同，但浆液扩散半径随注浆时间和注浆压力增长变化的幅度不同，相对来说更接近于实际。

(4)宾汉姆流体浆液扩散公式的推导主要基于浆液的流体特性，而对于裂隙岩体只考虑了裂隙的宽度。实际上，岩体裂隙宽度在围岩环境中不仅是变化的，而且还有一定的方向性，浆液在裂隙中流动时还要受到一定的摩阻力。因此，这些公式的计算结果往往偏大。

[1] 张民庆，彭峰.地下工程注浆技术[M].北京:地质出版社，2008．

[2] 汪磊，李涛,等.海底隧道预注浆加固效果检查与评价[J].铁道标准设计，2010(12):83-88.

[3] 曲立清，王全胜，张文强.胶州湾海底隧道综合超前地质预报与注浆方案选择[J]. 铁道工程学报，2009(9):64-68.

[4] 张玉侠.水泥浆液在裂隙岩体中的流动沉积机理研究[D].山东科技大学，2007(5):13-15.

[5] 邝健政，昝月稳，等.岩土注浆理论与工程实例[M].北京：科学出版社，2001．

[6] 阮文军.基于浆液粘度时变性的岩体裂隙注浆扩散模型[J].岩石力学与工程学报，2005(8):2709-2713.

[7] 阮文军.注浆扩散与浆液若干基本性能研究[J].岩土工程学报，2005(1):69-73．

[8] 郝哲，王介强，刘斌.岩体渗透注浆的理论研究[J].岩土力学与工程学报,2001(7):492-496.

[9] 郝哲.岩体注浆理论与应用[M].北京：地质出版社，2006．

[10] 黄春华.裂隙灌浆宾汉流体扩散能力研究[J].广东水利水电，1997(2): 13-17.

[11] 刘嘉材.裂缝灌浆扩散半径研究[C]∥水利水电科学研究院科学研究论文集(第8集).北京：水利出版社，1982．

[12] 邹金锋，李亮，杨小礼.劈裂注浆扩散半径及压力衰减分析[J].水利学报，2003(3):313-318.