高速铁路混凝土桥梁徐变变形计算分析及控制措施研究

2013-01-17周东卫

铁道标准设计 2013年6期

周东卫

(中铁第一勘察设计院集团有限公司,西安 710043)

无砟轨道能适应高速铁路高平顺性和高稳定性的要求，但可调性很小，其结构的永久变形只能通过扣件进行调整以恢复其设计几何形状[1-3]。对于混凝土桥梁而言，如果后期徐变变形超出无砟轨道扣件调节范围，将对桥上线路的平顺性造成严重危害，甚至可导致轨道扣件破坏失效，对行车安全造成巨大隐患。因此，必须了解并控制铺轨后混凝土收缩徐变引起的桥梁线形和轨道结构的改变，将其限制在无砟轨道扣件可调量程范围内。基于上述工程背景，在分析研究桥梁后期徐变变形对无砟轨道平顺性影响的基础上，提出如下徐变变形工程控制措施：首先通过模拟实际的施工方法与施工过程对结构进行分析，以计算出混凝土桥梁各截面点总的变形量以及每一个时期的变形量，然后采用实物变形测量得到的徐变实测数据修正理论变形量的偏差，最后根据轨道工程各施工阶段的具体情况，在计算底座板、加密基标和道床板断面点坐标时将剩余徐变效应引起的垂直位移量提前预留，从而大大减少桥梁后期徐变变形对无砟轨道铺设后平顺性的影响。本文的研究成果可为我国客运专线无砟轨道混凝土桥梁的工程实践提供参考和技术储备。

1 无砟轨道混凝土桥梁徐变效应的计算方法

1.1 徐变效应的计算方法

为了尽可能减少混凝土徐变变形对轨道铺设后的影响，施工单位进行各工序施工作业的不同阶段，均需由设计单位提供其在综合考虑梁型、梁长、桥梁的施工方法、混凝土的龄期、施加二期荷载的时间、预应力的张拉时间等因素的情况下，计算出由徐变引起的总变形量以及每一时期的变形量的理论值。徐变计算根据加载龄期与徐变系数关系的不同假定，主要有如下几种计算模型[4]：有效模量法、徐变率法、叠加法、流动率法、继效流动理论及按龄期调整的有效模量法等。这些方法都假定徐变与应力关系是线性的，并服从叠加原理。

无砟轨道混凝土桥梁的徐变效应计算过程如下：①将桥梁理想化为在节点处互相连接的平面梁单元的组合，每个单元的龄期、收缩徐变特性、材料特性及截面特性需根据结构尺寸和施工方案具体确定，假设每个单元温度分布相同。②将结构经受收缩徐变的过程划分为与施工过程相适应的时段(如建造新单元、张拉预应力筋、体系转换、施加施工荷载等)。③在每一时段，都对当时已形成的结构进行一次全面的分析，求出该时段内产生的全部节点位移增量和节点力增量(即结构内力和变形的增量)，上述增量与本时段开始时的节点位移、节点力相加，即可得出本时段结束时的节点位移和节点力的状态。按照这一方法，即可得出任意施工阶段结构的内力和变形状态，从而实现对混凝土桥梁从开始施工到成桥以及收缩徐变完成这一整个过程中任意时刻的内力和变形状态的跟踪分析。④计算出各施工放样断面点在相应梁跨的局部坐标系中的位置，然后根据计算出的理论徐变变形分布数据进行内插，即可计算出各施工放样断面点的理论徐变变形值。⑤计算出徐变效应在各施工放样断面点处引起的变形量后，对应施工断面点的放样高程采用该变形量进行改正，即完成了考虑徐变效应的施工断面计算，从而在施工过程中对后期徐变变形的影响提前进行了预留。图1为国内某客运专线32.6 m预制梁终张拉后各节点徐变理论变形值。

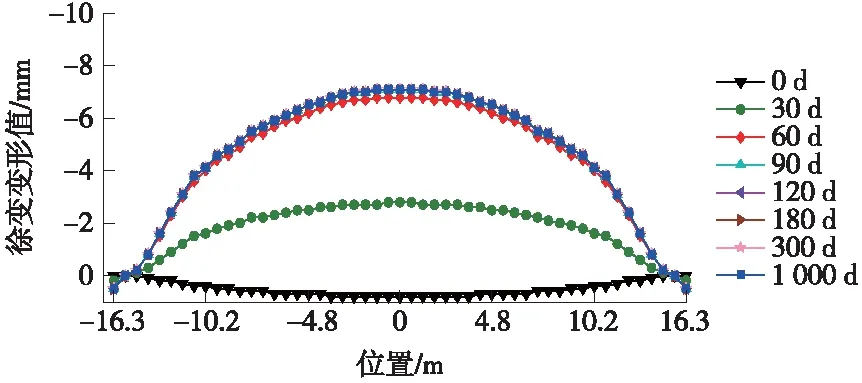
图1 某客运专线32.6 m预制梁徐变理论变形值

1.2 徐变修正系数的计算方法

由于徐变变形的复杂性和计算理论的局限性，通过理论计算的徐变变形值与实际观测存在一定的偏差，实际作业中往往需要借助实物变形测量的方法来修正计算中所得到的数值，提高理论计算结果与实际变形的接近程度。

在无砟轨道不同施工阶段的断面数据计算中，桥梁底座板断面数据、轨道基准点、加密基标数据以及轨道板精调数据和道床板断面数据的计算中，均需考虑剩余徐变效应对上述施工数据的影响。计算时首先需要确定出桥梁各截面点在终张拉后各时间节点的“实际徐变变形值”，然后在计算施工数据时考虑“采用比例”。由于徐变理论变形值计算并非十分准确，因此在实际操作中需要对理论计算值进行修正，通过对桥梁终张拉后各截面点进行定期徐变观测求得其在各时间节点的实测变形值，将实测变形值除以理论变形值即求得修正系数，即实际徐变变形值=理论计算值×修正系数，而实际最终采用值=实际徐变变形值×采用比例。如修正系数=实测值/理论值，即求得该梁在终张拉后60、90 d和180 d的理论变形修正系数。采用比例依据理论徐变计算的准确程度、实测数据的观测频次和精度情况等因素综合确定。

为了保证求取的修正系数具有较高的准确性和可靠性，计算修正系数需遵守如下原则：①应以梁场为单元计算各种梁型的修正系数；②一类梁型的观测数据少于5片梁时，不做分析；③徐变观测时间短于180 d时，不做分析；④观测数据明显不合理时，不做分析；⑤梁型定义不清楚的，不做分析。待修正系数正确求解后，即可将修正系数用于修正该梁场生产的该种梁型理论计算值的偏差，从而可根据不同的施工阶段将剩余徐变变形在轨道铺设后的变化量提前预留，以充分满足轨道扣件可调整量的要求，保证轨道的平顺性和行车安全。图2为某梁场生产的32.6 m预制梁终张拉后60 d理论徐变变形值修正前后各截面点的差异图。

图2 某梁场32.6 m预制梁徐变理论变形值修正前后

2 徐变变形计算分析

为了分析混凝土桥梁后期徐变变形对无砟轨道底座板断面、轨道基准点数据以及轨道板精调放样的影响，以京沪高速铁路为例，按本文阐述的徐变效应计算方法，在综合考虑了梁型、梁长、桥梁施工方法、混凝土龄期、施加二期荷载的时间、预应力张拉时间等因素的基础上，对各种桥梁徐变变形引起的垂直位移变化以及部分梁场混凝土预制梁的修正系数进行了计算与分析。

2.1 理论徐变变形值计算分析

本文对京沪高速铁路部分梁型的理论徐变值进行了计算分析。徐变计算考虑了桥梁终张拉后的时间、混凝土的龄期，但未包括墩台变形、变位及温度变化产生的挠度。时间节点分别为终张拉后0、30、60、90、120、150、180、300、1 000 d(按10 d终张拉、终张拉后90 d二期恒载一期上桥、终张拉后180 d二期恒载二期上桥、终张拉后210 d二期恒载三期上桥考虑，混凝土徐变按1 500 d考虑)，表1统计了每种梁型从终张拉后60 d到180 d的徐变变化最大值。

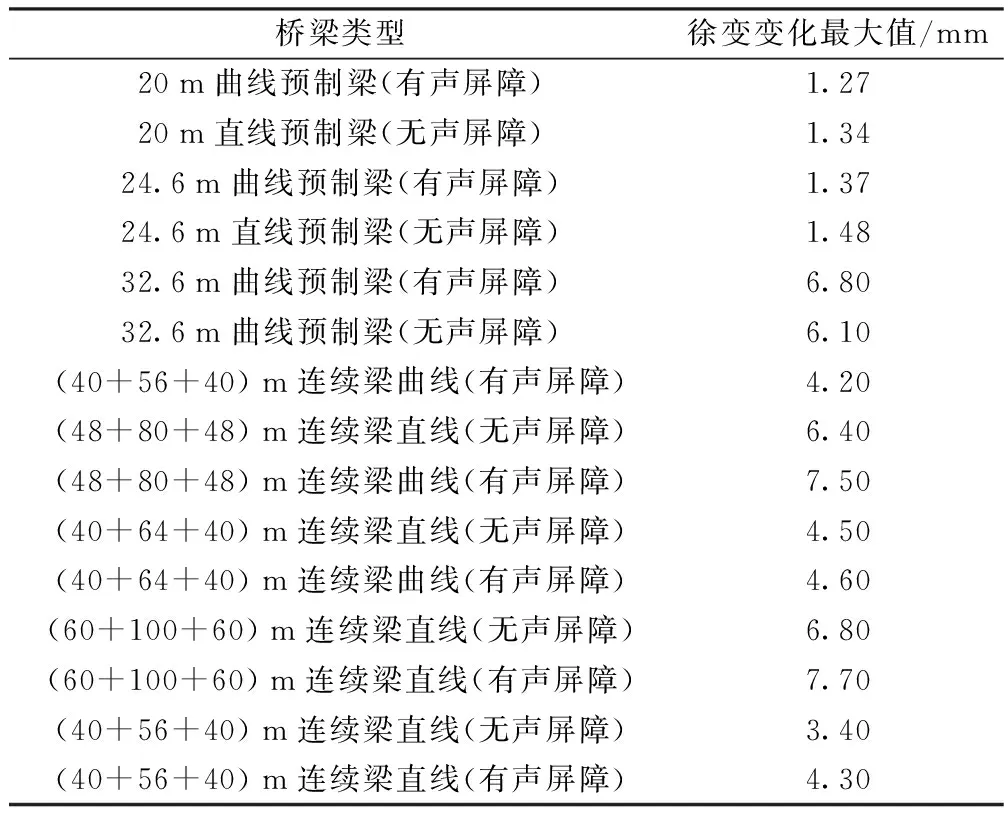
表1 京沪高铁部分桥梁终张拉后60～180 d理论徐变变化值

从表1可以看出，60～180d的理论徐变变化量的最大值达7.70 mm，且大跨连续梁的徐变变形值通常要大于预制梁，说明桥梁结构剩余徐变量对轨道工程会造成较大的影响，终张拉60 d后无砟轨道不同的施工阶段计算底座板断面、轨道基准点数据和轨道板精调断面时，必须顾及桥梁结构剩余徐变量对轨道工程的影响，同时还需考虑未上桥二期恒荷载引起的弹性变形(对已上桥的二期恒荷载的影响不再考虑)。通过对京沪高速铁路徐变变形数据统计分析后发现，70%的徐变变形在终张拉后180d之内发生，因此为了简化计算，一般在终张拉后180d就可不再考虑剩余徐变变形的影响。

2.2 梁场修正系数计算分析

本文以梁场为单位计算了各梁场生产的32.6 m预制梁的理论徐变变形值的修正系数。由于京沪高速铁路全线的预制梁计算修正系数时都已超过2个月，因此，0、30 d的变形采用理论值，不做修正，观测值对理论值的修正时间节点为60、90 d和180 d，即确定该三时间点的修正系数。表2统计了部分梁场的32 m梁的徐变修正系数。表3为采用表2修正系数对32.6 m预制梁终张拉后60～180 d进行修正前后的跨中变形值。

表2 京沪高铁部分梁场32.6 m梁修正系数(无量纲)

表3 京沪高铁部分梁场32.6 m预制梁修正前后徐变变化值统计 mm

从表2、表3可以看出，京沪高速铁路3个预制梁场的32.6 m直线预制梁终张拉后60～180 d某些时间节点的徐变修正系数仅为0.5，变形量差异最大达4.6 mm，这是由于影响徐变效应的因素较多，理论模拟计算值具有一定的误差，因此理论变形值必须经过实测数据修正后才能用于对无砟轨道铺设后剩余徐变变形量的估计，确保后期徐变变形估计的准确可靠。通过在各施工断面点坐标计算时对其提前预留，从而有效控制后期剩余徐变变形对施工或运营期间轨道平顺性的影响。