地铁小半径曲线钢轨波磨影响因素分析
2013-01-17王洪刚
王洪刚,肖 宏,彭 华
(北京交通大学土木建筑工程学院, 北京 100044)
钢轨铺入线路以后,受到车辆的循环荷载,在钢轨表面会产生不同程度的磨损,而波磨是其中影响行车质量的一种轨面磨损。波磨是世界各国城市轨道交通面临的普遍问题,各国铁路研究人员对此问题的研究也由来已久,并且提出了一些相应的整治措施。钢轨的波磨是一个周期性的不平顺缺陷,列车经过波磨钢轨地段时会引起轮对、转向架和车体的上下剧烈振动,加大了轮轨之间的动力作用,加速了机车车辆及轨道部件的损坏,增加了运输设备养护维修费用,缩短了钢轨的更换周期,严重时危及行车安全,此外,钢轨踏面波磨的存在降低了旅客列车的舒适度,并且还是城市噪声的主要来源。
有关钢轨波磨的成因,各国铁路研究工作者曾经提出过各种不同的见解。其中有些解释具有一定的理论依据,也有一些解释尚处于推测阶段。本文应用动态蠕滑理论对其形成的机理进行分析,并通过对某市地铁小半径曲线典型路段钢轨波磨的数值分析进行验证,研究其磨耗的特点和发展规律。
1 滚动接触面蠕滑力分析
车轮通过曲线时,不可能总是出现纯滚动,车轮真实的前进速度并不等于其滚动形成的真实前进速度,车轮相对钢轨会产生很微小的弹性滑动,即蠕滑。轮轨接触面上的切向力与轮轨间蠕滑的大小有关,即蠕滑力[1]。在车轮产生大蠕滑以致打滑的情况下,蠕滑力趋于饱和,最大的蠕滑力即为库仑摩擦力。在小半径曲线上,单靠轮踏面蠕滑导向是不够的,还必须依靠导向轮轮缘力进行导向。
Kalker[1]在De Pater所设想的基础上,完成了两个弹性体滚动接触的线性理论。Kalker在开展线性理论研究时,利用了Halling等人的理论成果[3-4],该理论认为,当各项蠕滑率都很小时,滑动区就很小,其影响可以忽略。在Kalker线性理论中,假定接触区全部为黏着区,且切向力的分部对称,因此纵向蠕滑力与横向蠕滑率无关,而横向蠕滑力也与纵向蠕滑率无关。给出了蠕滑力与蠕滑率的线性公式
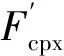
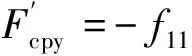
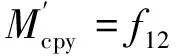
式中f11,f12,f22,f33——轮轨之间的横向、旋转/横向、自旋、纵向蠕滑率系数;
εx,εy,εsp——轮轨之间的纵向、横向、旋转蠕滑率;
ξ——缩减因子。


式中μ——轮轨之间的摩擦系数;
FN——轮轨踏面之间的法向作用力。
f11=G(ab)C22,f12=G(ab)3/2C23
f22=G(ab)2C33,f33=G(ab)C11(6)
式中G——材料的剪切模量;
a,b——轮轨接触斑椭圆的长半轴和短半轴;
Cij——无量纲的Kalker系数,其大小与轮轨接触斑的长、短半轴及材料的泊松比ν有关。
因此可得作用于车轮踏面上3个方向的蠕滑力,这里选取左侧轮轨蠕滑力来说明问题,用Kalker线性理论提供的方法计算蠕滑系数,简便实用,又有一定精度,被广泛应用[5]。左侧车轮蠕滑力如下
x方向FcxL=FcpxL-φωFcpyLcos(δL+φω)(7)
y方向FcyL=φωFcpxL+FcpyLcos(δL+φω)(8)
z方向FczL=FcpyLsin(δL+φω) (9)
式中φω——轮对摇头角;
φω——轮对侧滚角;
δL——左轮轨间接触角。
由Hertz[6-8]理论可以计算两弹性体的接触面积。轮轨接触是两个弹性体接触,两个弹性体可以由不同的材料组成,用Hertz理论求解可以得到轮轨接触斑的形状及接触斑纵向的长半轴a和短半轴b,即
a=m33πP(K1+K2)4K3,b=n33πP(K1+K2)4K3
式中P——轮轨之间的正压力。
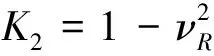


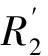
νω,νR——车轮材料和钢轨材料的泊松比;
Eω,ER——车轮材料和钢轨材料的弹性模量。
如果接触体的圆心在物体内部,则认为曲率为正,否则为负。在计算a和b中的m,n系数时取决于K3,K4。K4的计算公式如下


式中ψ——包含两个主曲率1/R1、1/R2法平面之间的夹角。
θ=arccos(K4/K3)(11)
求出θ角以后,可以查表求得m、n,继而可以求出轮轨接触斑的面积。
轮轨间纵横向蠕滑力代表轮轨间相对滑移摩擦产生的作用力,蠕滑力越大,钢轨的磨耗将越严重,当出现持续的饱和蠕滑力时,会造成钢轨波磨现象的出现。
磨耗功率主要反映钢轨波磨的情况,可以由下式表达[9]
W1=Fxεx+Fyεy+Fspεsp(12)
式中,Fx,Fy,Fsp分别为纵向、横向蠕滑力和法向蠕滑力;εx,εy,εsp分别为纵向、横向蠕滑率和自旋蠕滑率。
磨耗功率代表消耗在轮轨接触面上的功,磨耗功率数值越大,钢轨顶面磨耗程度越严重; 当出现持续不衰减的波动时,会造成钢轨波磨现象的出现[10-11];波动的幅值越大,波磨出现越快,程度越严重。
磨耗功率和轮轨间纵横向蠕滑力在实际工程中应用方便,同时精度满足要求,故主要选取二者作为钢轨磨耗的评价指标。
2 模型建立
车辆模型参数选取地铁B型车[12],车长19 m,车体最大宽度2.8 m,高度3.0 m,车体质量22 800 kg,车辆定距12.6 m,轴距2.2 m,轮对质量1 040 kg,转向架质量7 000 kg,一系、二系弹簧(空气弹簧)纵向、垂向、横向刚度按实际B型车参数设定。
分析路段选取某市地铁小半径曲线异常波磨路段,几何参数见表1。典型路段曲线半径350 m,采用剪切型减振器扣件和普通短轨枕道床,扣件刚度为10 kN/mm。钢轨选用60 kg/m钢轨,弹性模量2.07×1011N/m2,泊松比0.3。整体道床采用C30混凝土,密度2500 kg/m3,泊松比0.2,弹性模量3.00×1010N/m2。

表1 典型路段参数
3 曲线半径对钢轨磨耗的影响
选取某市地铁曲线路段半径在300~1 000 m范围内变化,车辆运行速度为60 km/h。曲线半径对磨耗功率波动情况的影响如图1所示。随着曲线半径的增大,第一轮对磨耗功率的波动性逐渐减弱,磨耗功率数值由半径300 m时的3 kN·m/s降低为1 000 m时的0.5 kN·m/s;第二轮对磨耗功率的波动很小,且随曲线半径的增大而减小,由半径300 m时的0.25 kN·m/s降低为1 000 m时的0.025 kN·m/s,减小近10倍。从表2可以看出,半径大于500 m后磨耗功率的波动范围开始明显减小,半径为800 m后磨耗功率的波动性基本消失了,意味着在大半径曲线上钢轨波磨得到了有效的控制。曲线半径从300 m增加到1 000 m,一位轮对磨耗功率降低约83.3%,二位轮对磨耗功率降低约90%。由此可知增加曲线半径可以有效降低钢轨的磨耗。

图1 曲线半径对磨耗功率的影响情况

表2 一位轮对磨耗功率随曲线半径变化的波动范围
曲线半径对横向蠕滑力的影响见图2,曲线半径由300 m增大到500 m时,横向蠕滑力逐渐增加,一位轮对增加量为72.2%,二位轮对增加量为12.5%。曲线半径由500 m增大到1 000 m时,一位轮对横向蠕滑力降低约35.4%,二位轮对横向蠕滑力降低44.4%。这表明在曲线半径为300 m时,轨距加宽降低了轮轨横向蠕滑力的作用,且随着曲线半径的增大,轨距加宽值逐渐减小。当半径为500 m时,曲线地段不再加宽,车辆依靠蠕滑导向的作用最明显,曲线半径大于500 m后,轮轨间的横向蠕滑力逐渐降低,钢轨磨耗也随之下降。
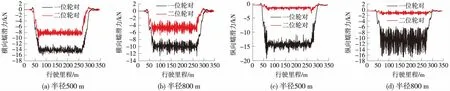
图2 曲线半径对蠕滑力的影响情况
曲线半径由300 m增大至500 m时,一位轮对的纵向蠕滑力受曲线半径变化的影响较为明显,纵向蠕滑力降低36.3%;曲线半径500~1 000 m范围内,纵向蠕滑力趋于平稳,为15~17 kN。二位轮对的变化规律与一位轮对相似,纵向蠕滑力在300~500 m范围内降低较为明显,降低71.4%,500~1 000 m范围内纵向蠕滑力基本没有变化,为2 kN。即地铁曲线半径大于500 m时,轮轨间的纵、横向蠕滑力均明显减小,有利于降低钢轨磨耗。图3为曲线半径对蠕滑力的影响曲线。

图3 曲线半径对蠕滑力的影响曲线
4 运营速度对钢轨磨耗的影响
计算工况与前面第3节相同,典型路段圆曲线长200 m,缓和曲线长60 m,曲线超高为120 mm,线路全长360 m。图4显示速度为50、60、70、80 km/h时,磨耗功率随车速的变化情况。
一位轮对的磨耗功率随着车速的增加而上升,由图5可以看出,30~50 km/h范围内曲线斜率较缓,50~60 km/h范围内的增加量最为明显,约为42.8%,60~80 km/h时磨耗功率增加量约为40%,可以看出速度为60 km/h以后磨耗功率的增加量开始减小。从表3可以看出,车速50 km/h与60 km/h时磨耗功率的波动幅值为0.9~1.25 kN·m/h,当车速为70 km/h时,磨耗功率波动幅值增加到1.6 kN·m/h,速度为80 km/h时波动幅值为2 kN·m/h,即70 km/h之后磨耗功率大幅增加,对钢轨磨耗不利。二位轮对的磨耗功率随车速的变化很小,为0.12~0.25 kN·m/h。基于本研究模型和工况,得出最高运营速度在60~70 km/h对减缓钢轨磨耗有利。
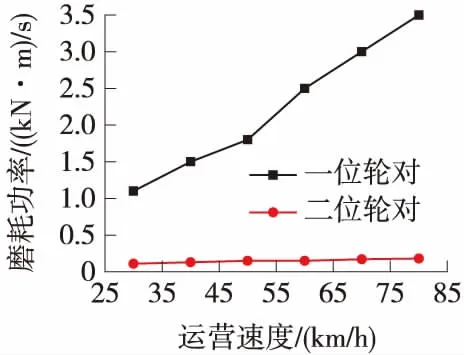
图5 车速对磨耗功率的影响曲线
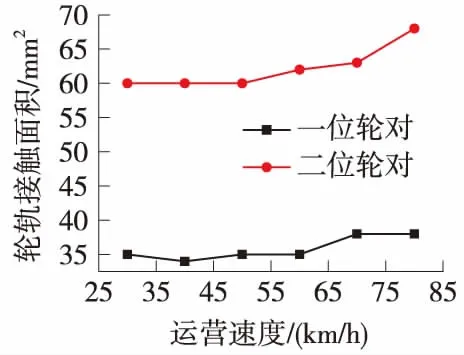
图6 车速对轮轨接触面积的影响曲线
由轮轨接触面积同运营速度的关系曲线图6中可

表3 一位轮对磨耗功率随车速变化的波动范围
以看出,第一轮对轮轨接触面积维持在33~38 mm2,第二轮对轮轨接触面积运营速度在30~50 km/h时保持不变,为60 mm2,当运营速度大于50 km/h时,轮轨接触面积逐渐增大,车辆运行趋于平稳,同样可以得出结论:最高运营速度在60~70 km/h时为宜。
5 结论
针对地铁小半径曲线地段钢轨磨耗的情况,从轮轨蠕滑力和磨耗功率的角度分析钢轨波磨的机理,利用多体动力学仿真软件SIMPACK特有的轮轨模块,从运营条件和曲线参数角度分析了地铁车辆通过小半径曲线时钢轨磨耗的情况。基于计算结果得到以下结论。
(1)曲线半径是影响钢轨波磨的最主要因素,在允许的条件下宜采用大半径曲线。本文数值计算结果表明,曲线半径应尽量大于500 m。
(2)合理设定车辆的运营速度可以降低钢轨的磨耗。由分析结果可知,最高运营速度设置为60~70 km/h,可以在运力与降低钢轨磨耗间找到较好的平衡点。
实际上,钢轨波磨除受以上所探讨的参数影响外,还要受到轨道刚度、轨底坡及车辆构造等其他因素的影响。本文主要从车辆运营条件和线路条件的角度出发,对地铁小半径曲线钢轨波磨问题做了一些对比分析,最终需要将仿真分析与现场试验数据结合验证,确定地铁小半径曲线地段钢轨波磨的成因及有效减磨措施。
[1] Grassie S L. Rail corrugation: Characteristics, Causes and treatments[J]. Rail and Rapid Transit, 2008,223(F):581-596.
[2] 李成辉.轨道[M].成都.西南交通大学出版社,2005:81-82.
[3] 练松良,孙琦,王午生.铁路曲线钢轨磨耗及其减缓措施[M].北京.中国铁道出版社,2001:86-95.
[4] 金学松.轮轨蠕滑理论及其试验研究[M].成都:西南交通大学出版社,2007:32-35.
[5] 张立民.应用蠕滑理论分析钢轨表面磨耗型波浪形磨损[J].中国机械工程,2003,38(1):34.
[6] 沈刚,张学华,郭满鸿.地铁曲线波浪形磨耗的机理分析[J].同济大学学报,2011,39(3):381-384.
[7] 孙坡,张玉明.关于直线钢轨不均匀侧磨的研究[J].铁道标准设计,2011(9):20-23.
[8] 戴春阳,胡华峰,高亮,辛涛.地铁运营条件与线路参数对曲线钢轨波磨的影响[J].都市快轨交通,2011,24(5):6-10.
[9] 陈鹏,高亮,郝建芳.铁路曲线上钢轨磨耗影响参数的仿真研[J].中国铁道科学,2007,28(5):19-22.
[10] 贡照华,张琳.轨道结构状态分析及其控制[J].铁道标准设计,2005(3):72-73.
[11] 王瑞震,于春华.城市轨道交通工程轨道系统设计应注意的相关问题[J].铁道标准设计,2011(7):9-11.
[12] 北京城建设计研究总院.GB 50157—2003 地铁设计规范[S].北京:中国计划出版社,2003.
