基于改进型自适应锁相环的特定次谐波补偿算法在APF中的应用

刘 扬 谭国俊

（中国矿业大学信息与电气工程学院 徐州 221008）

1 引言

随着家用和工业系统中大量非线性负载的增加，导致电力系统中的电能质量逐渐下降。这些非线性负载主要包括电源、软启动、调速装置等，它们产生非正弦电流，导致公共连接点处的电压电流发生畸变。这些畸变的电能不仅会造成输配电设备发生故障，而且会影响生产领域的产品质量。例如设备过热、电容器鼓肚、中性点电流过大、低功率因数等。为了解决电能质量问题，文献[1-4]研究了多种类型的有源电力滤波器（APF），其中电压型并联APF是一种最有效的结构，它由主电路与控制电路两部分组成，控制电路包括谐波的检测、电流跟踪控制等环节。

在有源电力滤波器的控制方法中谐波检测是一项非常重要的环节，检测算法主要有FFT处理算法、基于瞬时无功的p-q和ip-iq法、小波变换等，这些算法需用到锁相环进行相位的跟踪，锁相环性能的好坏直接影响到谐波检测的准确性从而影响后续的补偿效果[5-7]。在有源电力滤波器的谐波检测中相位是一个非常重要的变量，受外部条件影响其可能变化平稳也可能发生突变。在锁相环中由于相位与频率在同一回路中，相位的突变可能引起频率的瞬变。同样频率的瞬变会反作用于相位，造成相位预测和同步延时[6,8]。为提高锁相环的性能，国内外学者进行了大量研究，文献[1]采用小数分频，降低了锁相环的量化噪声；文献[2]采用PID滤波器，设计了基于三态反相器的DCO；文献[3]利用自适应带宽，在宽范围内达到了低抖动。这些研究都是对锁相环的各模块进行改进，提高了锁相环的单项性能指标。未从整体上缩短锁相环的捕获过程。

在一些高电压大容量的场合并联型有源电力滤波器经常与无源滤波配合构成混合滤波装置进行使用。有源电力滤波器滤除特定次谐波，无源滤波装置滤除剩余谐波。研究有源电力滤波器的特定次谐波检测与补偿算法具有一定的实际意义。因此论文在文献[1-3]研究的基础上，主要进行两方面的工作：

（1）针对传统加强型锁相环相位/频率耦合问题，采取自适应方法对锁相环的增益进行调整，在频率预测回路中增加自适应增益以最大限度地降低由相位突变引起的频率瞬变。这种方法在降低频率瞬变和相位震荡的基础上极大地提高了相位信息的获取速度。

（2）在解决锁相环相位/频率耦合问题基础上，针对混合型有源电力滤波器补偿特定次谐波的特点，研究一种新型有源电力滤波器的特定次谐波补偿算法。

2 自适应加强型锁相环

2.1 传统加强型锁相环

图1所示为传统加强型锁相环，u为输入信号，y为预测输出信号，A为幅值，ω是角频率，φ是相位角，ω0为信号的额定频率且为一常数[4]。加强型锁相环的数学模型可以用以下方程表示

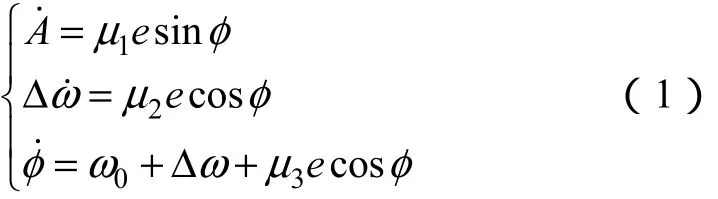
式中e——输入、输出信号之差，e=u-y；

μi——加强型锁相环增益，为正数，i=1, 2, 3。

由式（1）的近似线性化模型，可以得到幅值、相位/频率的传递函数

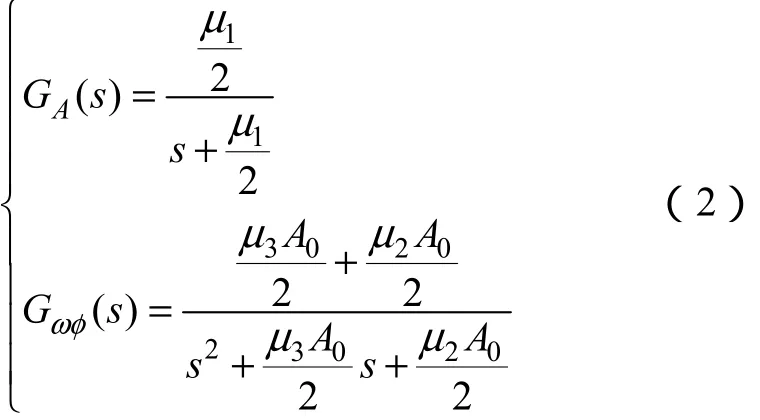
式中，A0为输入信号的幅值；本文中取μ1=μ3=μ=Kω0，μ2=μ2/8。

这样整个系统由单个增益K进行控制，这样K与反馈输出成正比，但是K过大或过小有可能引起系统震荡[3]，建议0.5＜K＜1.5，本文中取K=。

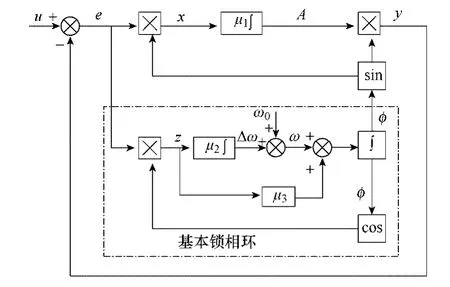
图1 传统加强型锁相环Fig.1 Traditional phase lock loop

从图 1可以看出角频率ω与相位角φ在同一闭环回路中，具有一定的耦合。因此在相位突变或锁相环刚开始工作时刻（此时锁相环未检测到信号的初始相位角），相位的变化会引起频率的变化如图2所示。由于电力系统中存在大量电机组成的旋转机械对频率较敏感，所以有必要对传统加强型锁相环进行改进。

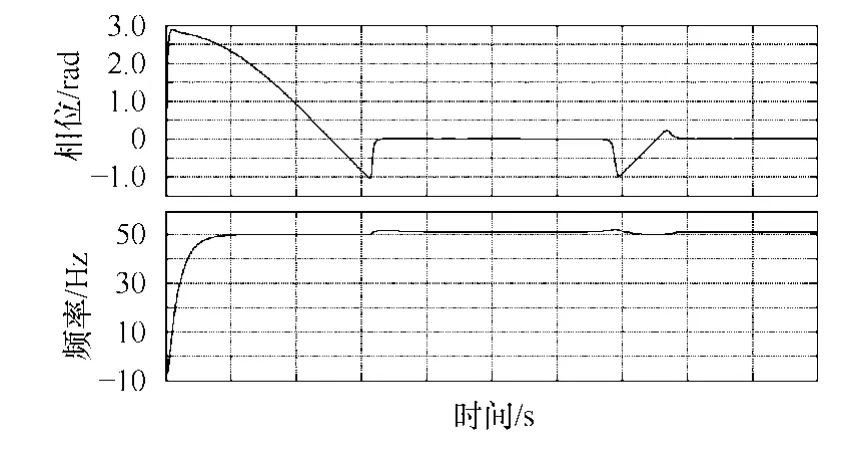
图2 相位变化对频率的影响Fig.2 Phase transformation effect on frequency

2.2 自适应加强型锁相环

增益μ2和μ3控制着相位/频率预测回路的性能，其中μ2反映了回路的带宽，μ2越大，带宽越宽，从而响应速度也越快。但是μ2的增大也加深了频率与相位的耦合。当相位跳变较大时，这种强耦合就会产生一系列问题。为了解决这个问题，驱动频率积分器的信号在相位跳变时必须进行限制，一种解决方法是使增益μ2自适应，即根据相位误差的大小进行调整。理想的解决方法是相位跳变越大，增益就越小，以减小对频率的不良影响。但是这种方法并不能够直接实现，因为相位的变化是未知的变量。但是从图1可以看出相位的跳变会直接反应于信号的误差：相位变化越大，信号输入误差也就越大。因此将μ2用代替可得自适应调整方法

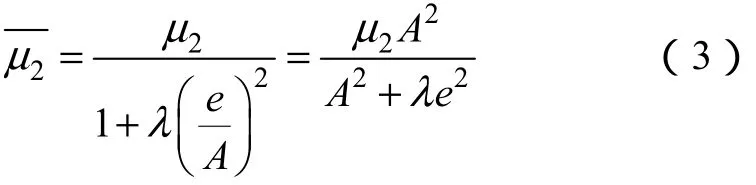
式中，λ是一个正常数；自适应增益随着信号的误差增大而减小，当输入信号差为零时=μ2。

常数λ的选择代表了自适应方法在相位突变过程中抑制频率瞬变的能力。λ越大频率受相位突变的影响也就越小，即调整时间越小[5]。然而如果λ过大，将会影响频率回路的速度。λ与调整时间的关系曲线如图 3所示，从图中可以看出λ越大各对应参数的调整时间就越小，当λ＞50时，调整时间的减小幅度显著减小；当λ＞100时调整时间几乎不随λ的增大而减小。因此λ的取值范围在50≤λ≤100，文中在仿真和实验时选择λ=100。

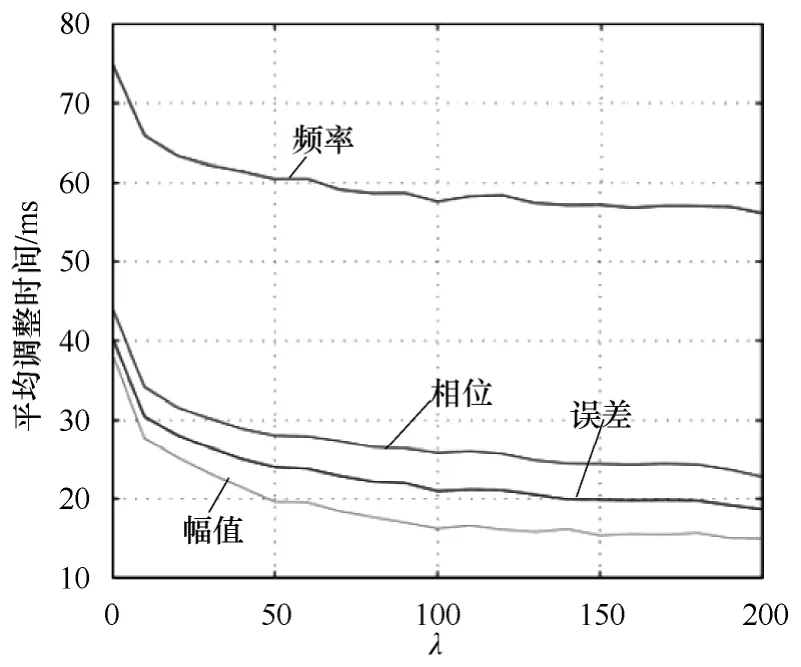
图3 λ 与调整时间的关系Fig.3 The relationship between time adjustment and λ

在实际应用中输入信号含有谐波成分，自适应增益的平均值小于μ2，因此系统的带宽响应变小，稳态精度提高。

图4 三相自适应锁相环控制框图Fig.4 Diagram of self-adaptive three-phase PLL

3 特定次谐波补偿算法

在混合型有源电力滤波器中，有源滤波部分只需补偿特定次谐波，因此需要对非线性负载产生的特定次谐波进行提取和补偿[6]，本文以自适应锁相环为基础，研究了一种新的特定次谐波补偿算法，对三相不平衡、谐波及频率瞬变有良好的补偿性能。

假设非线性负载电流ia(t) 经过傅里叶变换后为

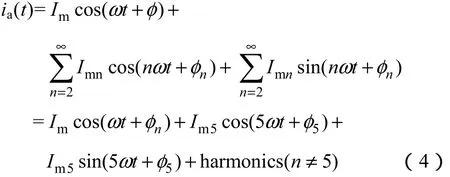
式中Im，Imn——非线性负载产生的基波以及n次谐波的幅值；

φ，φn——基波和n次谐波的相位；

Im5，φ5——5次谐波的幅值和相位。

获得非线性负载产生的5次谐波电流的幅值和相位后。就可以在公共连接点进行补偿。同理根据上述算法可以补偿任意次谐波电流。

4 仿真与实验

4.1 仿真

仿真在 Matlab/Simulink下进行[7,8]，各仿真主要参数见表1。

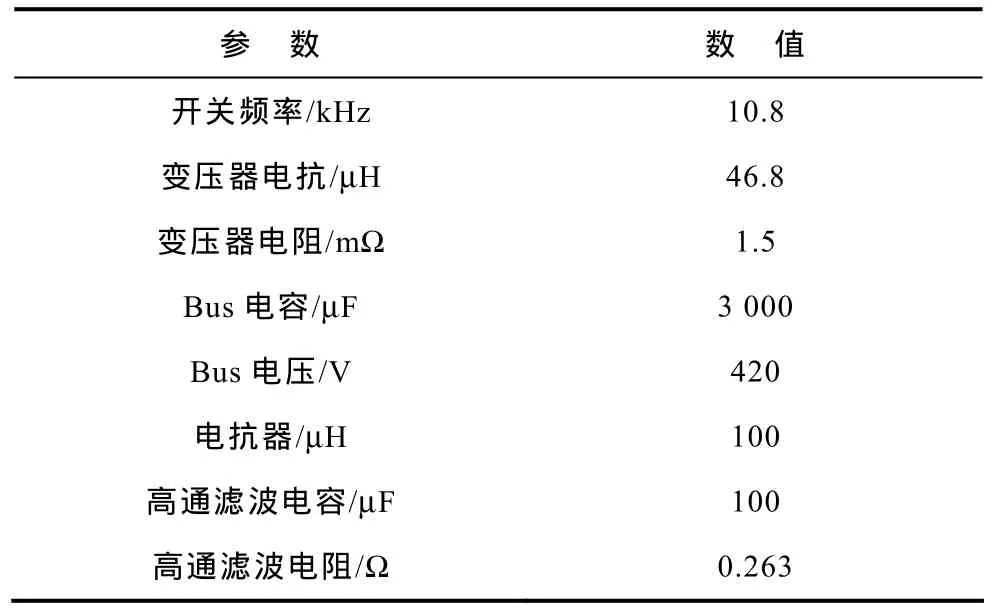
表1 仿真电路主要参数Tab.1 Simulation of electric circuit parameters

图 5a为传统锁相环与自适应锁相环的相位调整对比图，可以看出自适应锁相环在启动时刻调整优于传统锁相环。图5b为传统锁相环与自适应锁相环受相位扰动影响后频率变化对比图。可以看出自适应锁相环在开始阶段频率调整明显优于传统锁相环，且在运行过程中相位变化不会影响频率。图 6为输入信号加入5次谐波后传统锁相环与自适应锁相环跟踪效果对比。从图中可以看出当输入信号加入 5次谐波后，自适应锁相环的相位与频率经过0.05s捕获过程完毕，非常适用于谐波含量高的环境。图7a为补偿5次谐波前后波形对比图，5次谐波在 0.5s处开始补偿，图 7b为相对应的谐波柱状图。通过仿真可看出所提算法补偿效果良好。

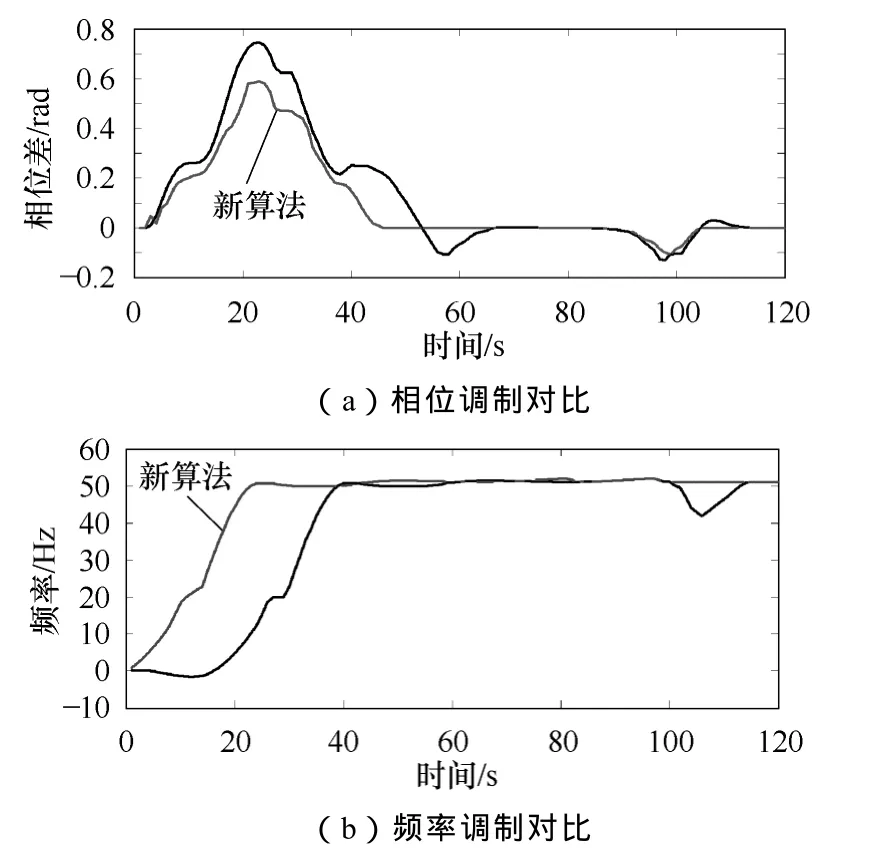
图5 两种锁相环调整对比Fig.5 Adjustment contrast between two PLL

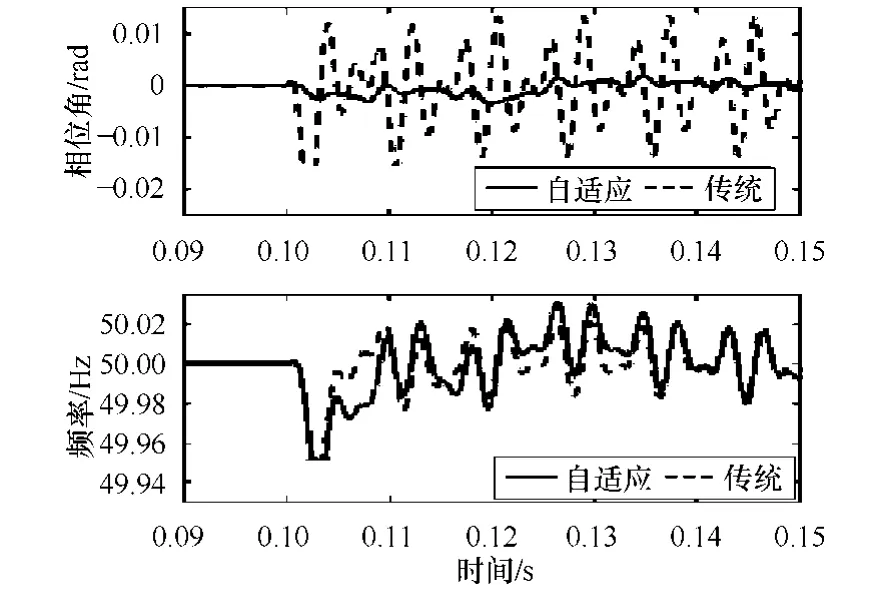
图6 加入5次谐波后传统锁相环与自适应锁相环跟踪效果对比Fig.6 Contrast of tracking results between traditional PLL and self-adaptive PLL after adding 5th harmonic

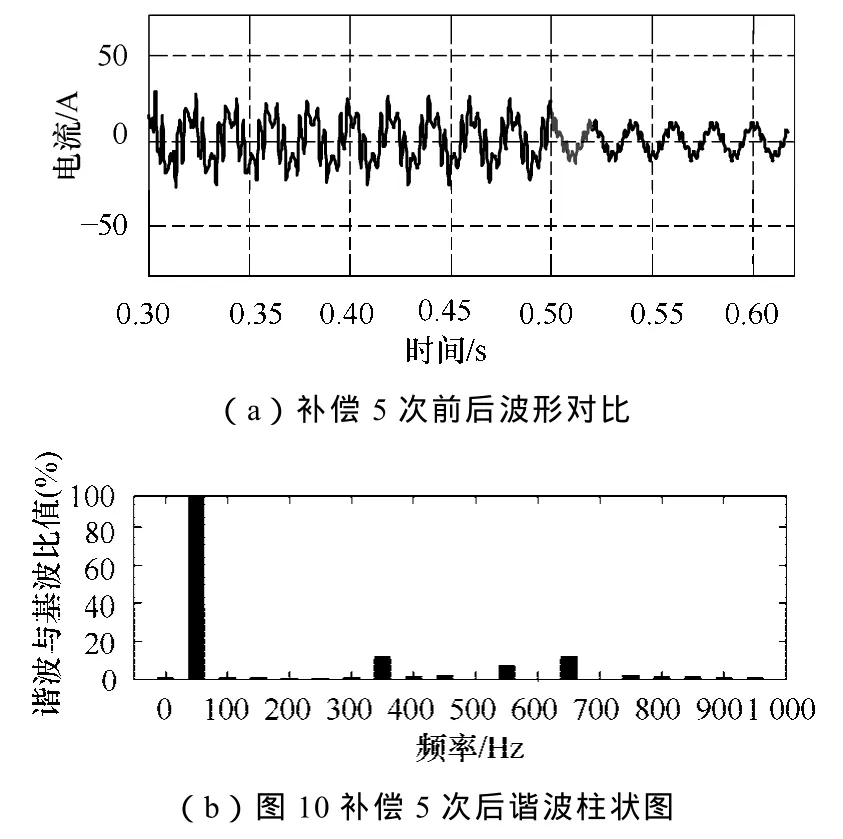
图7 补偿5次谐波对比图Fig.7 Contrast of waveform when the 5th harmonic was compensated

4.2 实验

为了验证仿真的正确性，对所提算法进行了验证性实验。实验在一套额定电流50A的有源电力滤波器实验平台完成，负载为三相三线制6脉波整流器，产生总谐波电流(15±0.6)A，约为有源电力滤波器额定电流的1/3。控制器采用具有DSP处理功能的赛灵思 FPGA，型号为 XC3SD1800A，功率模块采用英飞凌公司Econo Dual封装IGBT。实验系统参数同表1。

自适应锁相环在FPGA中的实现框图如图8所示，u[n]=u(nTs)为输入信号的采样结果，Ts为采样周期，Z-1为一个采样时刻的延时。

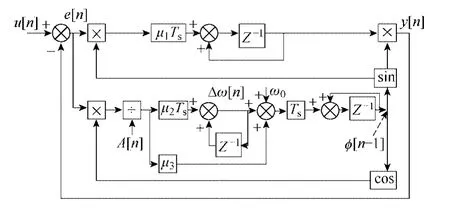
图8 自适应锁相环实现框图Fig.8 Schematic of traditional phase lock loop

选择补偿n次和k谐波的补偿算法控制框图如图9所示。

图9 特定次谐波补偿控制框图Fig.9 Schematic of specific harmonic compensatio n

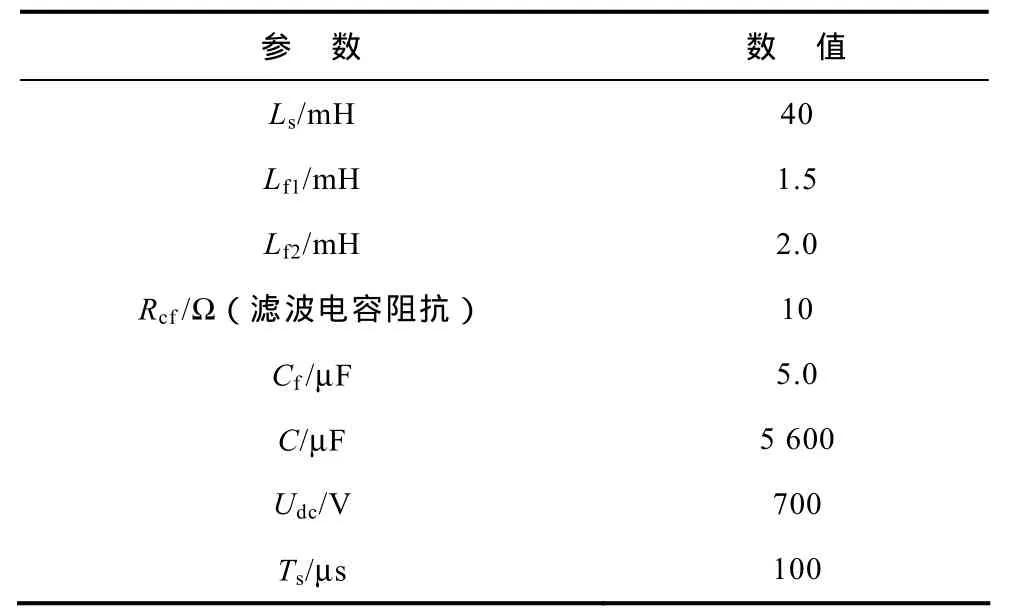
表2 系统主要参数Tab.2 System parameters

图 10为启动时刻相位变化对频率影响在两种锁相环中的对比图。图11为三相不平衡情况下自适应锁相环输出跟踪输入的效果图。图12为特定补偿5、7次谐波的补偿效果图。从图 11可以看出在 A相突变时，自适应加强型锁相环经过约一个工频周期调整结束，无大的波动。由图12也能看出基于自适应锁相环的特定次谐波补偿算法在有源电力滤波器中的应用补偿效果。从图中电流波形的变化可以看出该算法可以对特定次谐波进行补偿，且响应速度快，在一个周期以内完成补偿。

图10 相位变化对频率的影响Fig.10 Phase transformation effect on frequency

图11 三相不平衡情况下自适应锁相环跟踪效果图Fig.11 Tracking results of self-adaptive PLL which was in the unbalanced three-phase

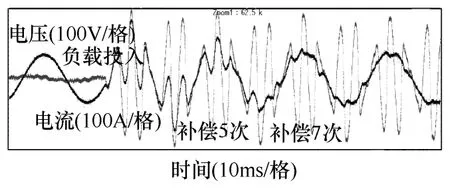
图12 特定5、7次谐波补偿实验Fig.12 Experimentation of specific 5th、7th harmonic compensation

5 结论

本文提出了基于自适应加强型锁相环的特定次谐波补偿控制策略，可用于重点补偿特定次谐波，特别适用于混合APF中。其中自适应加强型锁相环可以有效地降低相位变化对频率的影响，特定次谐波补偿控制策略简单，只需对需补偿的谐波乘以对应的参考电流即可提取出该次谐波。最后在理论分析的基础上对自适应加强型锁相环特定次谐波补偿算法进行了仿真与实验验证，仿真与实验结果证明了算法的正确性与有效性。

[1] Yu X, Sun Y, Zhang L, et al. A 1GHz fractional-N PLL clock generator with low-OSR ΔΣ modulation and FIR-embedded noise filtering[C]. IEEE International Solid-State Circuits Conference, 2008:346-347, 618.

[2] Tierno J A, Rylyakow A V, Friedman D J. A wide power supply range, wide tuning range, all static CMOS all digital PLL in 65nm SOI[J]. IEEE Journal of Solid-State Circuits, 2008, 42(6): 42-51.

[3] Kim J. Adaptive-bandwidth phase-locked loop with continuous background frequency calibration[J].IEEE Transactions on Circuits and Systems-II:Express Briefs, 2009, 56(3): 205-209.

[4] 刘健犇, 陈乔夫, 代少君, 等. 串联混合型有源滤波器直流母线电压控制策略[J]. 电工技术学报,2012, 27(9): 54-61.Liu Jianben, Chen Qiaofu, Dai Shaojun, et al. DC-link voltage control strategy of series hybrid active power filter[J]. Transactions of China Electrotechnical Society, 2012, 27(9): 54-61.

[5] 陶兴华, 李永东, 孙敏, 等. 一种基于同步旋转坐标变换的单相锁相环新算法[J]. 电工技术学报,2012, 27(6): 148-152.Tao Xinghua, Li Yongdong, Sun Min, et al. A novel single-phase locked loop algorithm based on synchronous reference frame[J]. Transactions of China Electrotechnical Society, 2012, 27(6): 148-152.

[6] 丁士启, 帅智康, 罗安. 一种新型注入式混合有源电力滤波器[J]. 电工技术学报, 2012, 27(1): 202-208.Ding Shiqi, Shuai Zhikang, Luo An. A novel injection type hybrid active power filter[J]. Transactions of China Electrotechnical Society, 2012, 27(1): 202-208.

[7] 刘亚梅, 惠锦, 杨洪耕. 电力系统谐波分析的多层DFT插值校正法[J]. 中国电机工程学报, 2012,32(25): 182-188.Liu Yamei, Hui Jin, Yang Honggeng. Multilayer DFT interpolation correction approach for power system harmonic analysis[J]. Proceedings of the CSEE, 2012,32(25): 182-188.

[8] 石磊, 单潮龙, 吴旭升, 等. 并联电压型中频有源滤波器注入电感的计算与分析[J]. 中国电机工程学报, 2011, 31(12): 252-258.Shi Lei, Shan Chaolong, Wu Xusheng, et al.Calculation and analysis of injection inductance for medium frequency shunt active power filter[J].Proceedings of the CSEE, 2011, 31(12): 252-258.