具备电容电压平衡和开关频率优化功能的五电平二极管钳位逆变器快速空间矢量调制

王姿雅 罗隆福 许德伟

（1.湖南大学电气与信息工程学院 长沙 410082 2.加拿大瑞尔森大学电气与计算机工程系 多伦多 M5B 2K3）

1 引言

二极管钳位多电平逆变器（Diode-Clamped Multi-Level Inverter, DCMLI）具有拓扑简单稳定、能提高输出电压波形质量、减小开关器件的电压应力和改善电磁兼容性等优点，在交流驱动、无功补偿、高压直流输电、有源滤波和电能调节储能系统等中高压系统中具有广泛地应用前景。

在理想情况下，DCMLI的直流侧电容均分直流电压，然而在实际运行中电容电压会因为电容的不规律充放电而偏离标准值，这一问题如果得不到有效地控制，将使得部分开关管承受过大的电压应力，最终可能烧毁开关管、并使逆变器无法正常工作。电容电压不平衡是影响 DCMLI应用的主要障碍，对于 DCMLI最简单的形式——三电平中点钳位逆变器，已有大量研究工作致力于解决其电容电压不平衡问题[1-4]。当超过三电平时，电压不平衡问题的复杂程度会显著增加，解决这一问题主要有两种方法：

第一类方法是从硬件方面入手，为 DCMLI的每个电容提供独立的直流电源[5]，或是给逆变器装备辅助电路[6,7]。这类方法不仅增加了额外的投资，同时使得系统更为复杂，对系统的维护和稳定运行都产生潜在的不良影响；第二类方法是利用多电平逆变器开关状态的冗余度通过调制算法选取最合适的冗余量构造开关状态序列从而实现电容电压平衡。文献[8-11]提出了空间矢量调制算法解决电压不平衡问题，这几种算法的基本思路是一致的，即首先建立电容电流与三相输出电流在不同开关状态下的数学模型，然后用一个以电容电流和电容电压为自变量的二次函数（也称能量函数）来反映逆变器的直流侧与交流侧在当前开关周期内所交换的能量，计算该函数在当前所有可选开关冗余状态下的值，取使得该函数值为最小的一组冗余量构成开关序列。文献[12,13]引入一个虚拟空间矢量的概念进行调制，在满足一定条件的前提下实现电压平衡，这一方法不是用常规空间矢量调制（Space Vector Modulation, SVM）的三个最近空间矢量（Nearest Three Vectors, NTV）来合成参考电压，其缺点是加大输出电压谐波含量和开关次数。这些研究为解决电压不平衡问题提供了可行的方法，但这些方法的计算量都非常大，并且它们都未提供能有效降低开关频率的措施。

本文提出了一种五电平二极管钳位逆变器（Diode-clamped Inverter, DCI）的SVM电容电压平衡方法。与上述调制方法不同的是，本文方法不需要进行任何四则运算，而只需要通过一定的逻辑比较运算从预定义的一组开关状态序列中选取最佳的一个序列完成调制。同时，本方法具有开关频率优化功能，可显著降低逆变器的开关频率。

2 五电平DCI的空间矢量调制

五电平 DCI（见图 1）的空间矢量调制是一种利用相关开关电压矢量来合成参考电压矢量Vref的数字调制技术。参考电压矢量和开关电压矢量通常在复平面上表示，所有电压矢量的起点都在复平面的原点上。复平面被均分为6个扇区，每个扇区跨60°，且分为16个三角形，三角形的一个顶点即代表一个开关电压矢量的终点。开关电压矢量用开关状态指示，除了位于扇区最外层的开关电压矢量，其他的电压矢量都具有一个以上的开关冗余状态。开关状态用（o，p，q）表示，其中o、p、q分别代表a、b、c三相连接到直流侧的节点，如图1所示。例如，状态 210表示在该状态下，a、b、c三相分别连接到直流侧的2号、1号和0号节点上。图2和图3分别是五电平DCI的空间矢量分布图和第1扇区的三角形排列图。

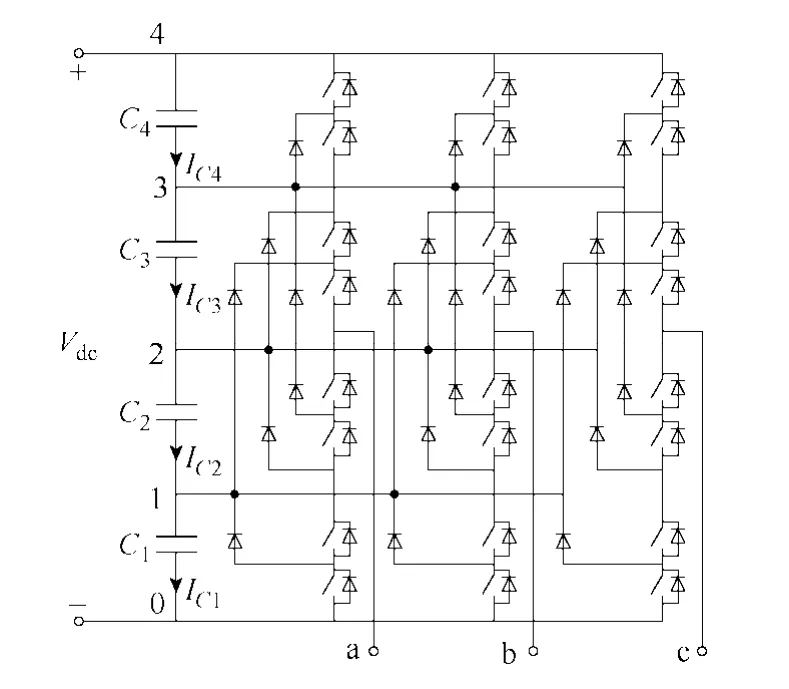
图1 五电平二极管钳位逆变器拓扑Fig.1 Topology of a five-level diode-clamped inverter

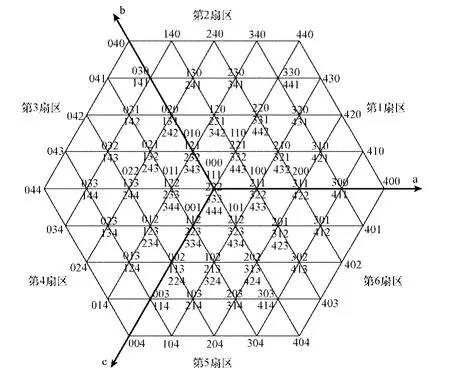
图2 五电平DCI的空间矢量Fig.2 Space vectors of a five-level DCI

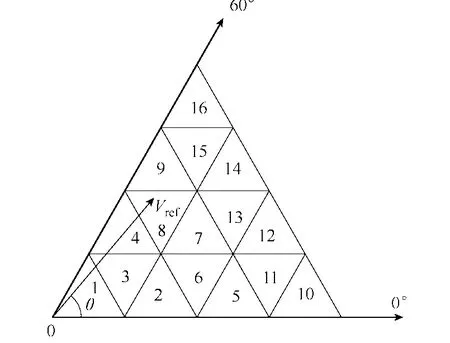
图3 第1扇区的三角形Fig.3 Triangles in sector 1

参考电压矢量Vref可能落在任一扇区的任一个三角形区域内，本文空间矢量调制算法的推导只针对于Vref落在第 1扇区的情形，当Vref落在其他五个扇区时，相应的调制算法能通过一定的映射关系获得，详见后文。进行空间矢量调制的前提是确定Vref的位置，当确定了Vref所在的三角形后，Vref即可由位于该三角形顶点的 NTV进行调制了。确定Vref的位置和NTV作用时间的方法和步骤在其他文献中已有详细介绍[14,15]，本文不再累述。一个空间矢量的不同冗余状态使得逆变器产生的输出电压波形是完全一致的，所不同的是它们对直流侧电容电压产生的影响。例如，对于空间矢量（100, 211, 322,433），状态 100将 a相连接到 1号节点、将 b、c两相连接到0号节点，因此DCI的交流侧和直流侧之间传递的能量都是通过电容C1完成的。当有能量输入 DCI时，C1充电，其电压升高；当 DCI输出能量时，C1放电，其电压降低。同理，状态 211、322和433将分别影响电容C2～C4的电压。正因为同一个开关矢量的不同冗余状态会对四个电容的电压产生不同的影响，因此才有可能通过调制算法选取恰当的开关状态在合成给定参考电压矢量的同时实现电容电压的平衡。

3 基于有功电流的电容电压平衡方案

3.1 电压平衡方案的原理

电容电压偏离标准值是由于电容的不规律充放电造成的，因此，要使偏离的电容电压回归并保持在标准值应从电容的充放电入手。当有能量输入逆变器时，肯定有电容会发生充电导致其电压升高，当能量从逆变器输出时，肯定有电容发生放电致其电压下降。如果能根据当前能量的传递方向和四个电容的电压偏移程度来选取合适的开关状态序列，则有可能实现电容电压的平衡。能量的传递方向可通过判断有功电流Id的方向获取，Id则是由逆变器的三相电流经过派克变换得到的。若Id＞0，则能量输入逆变器，此时电压下降最多的电容应尽可能多地充电，而电压升高最多的电容应尽可能多地放电，满足以上条件的开关状态序列即是最佳选择；同理，若Id≤0可以进行类似的判断。

不同于基于能量函数的平衡方案在每个开关周期内通过计算来选取开关状态组成开关序列，本文方案的开关序列是依据一定的原则预定义好的。首先，本文采用的开关序列是五段式的而非一般常用的七段式序列，这样可以减少每一个开关序列所关联的电容数，方便对电容电压的控制，同时可以降低一个开关周期内的器件开关动作次数。其次，在构造五段式序列时亦要遵循一定的规则，即从一个开关状态变换到下一个开关状态时，只使得位于同一个桥臂上的两个开关器件动作，其中一个导通、另一个关断，这意味着在一个开关周期内的任一次状态变换都只引发某一相的电压产生一级电平的变化，而另外两相的电压保持不变。一旦确定了参考电压矢量所在的三角形，也即确定了用于合成参考电压的NTV，则可能参与调制的开关状态也就确定了，同时，按照前述原则能够构造的开关序列集也就确定了。因此，图3中的每一个三角形都对应着一个确定的开关序列集，作为一个例子，表1给出了第1扇区8号三角形的开关序列集，表中的V1、V2、V3代表8号三角形对应的NTV。不管平衡算法从序列集中选取哪一个开关序列来合成参考电压，都能保证在每一个开关周期内只发生最少次数的开关器件动作，从而有效降低开关损耗，这也是本文算法相较于前述调制算法的一大优势之处。

表1 第1扇区8号三角形对应的开关序列集Tab.1 Sequence group for triangle 8 in sector 1

3.2 第1扇区的电容电压平衡算法

图3中第1扇区的16个三角形各自拥有对应的空间矢量和开关序列集，因而需要为每个三角形编制独立的平衡算法。由于这些算法依据相同的原理，它们的推导过程都是类似的，因此下面仅以8号三角形为例推导其对应的平衡算法。

平衡算法的目标是要通过逆变器与电网之间的能量交换来消除或减小偏移程度最大的电容的不平衡度，实现这一目标的前提是要掌握电容电流在不同冗余状态下的方向。电容电流的正方向如图1中的箭头所定义，若流经一个电容的电流方向为正，则该电容将被充电，其电压升高；反之则电容放电、电压下降。与第 1扇区的 8号三角形相关的 NTV为：V1（320, 431）、V2（210, 321, 432）和V3（220,331, 442），在对应的八个开关状态下四个电容电流用逆变器三相电流表示的关系式见表 2。结合表 1与表2可知，不同的开关序列将对电容电压的变化产生不同的影响。以电容C1为例，表1中的6号序列431-432-442-432-431不会对C1的电压产生影响，因为在构成该序列的三个状态431、432和442下电流IC1都为零（见表 2），C1就既不会充电，也不会放电；而1号序列210-220-320-220-210将直接影响C1的电压，因为在1号序列下IC1都等于Ia+Ib，Ia+Ib的方向为正或为负就决定了在1号序列下C1是一直充电或一直放电的。同时从表2可知，当用8号三角形的NTV进行调制时，四个电容的电流只会有三种可能的取值，即

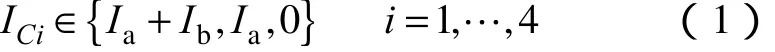
表2 电容电流与相电流的对应关系Tab.2 Relations between capacitor currents and phase currents

通过有功电流不仅可以判断能量传递的方向，同时还可以借助一些特殊的冗余状态确定部分电容电流的方向。这类特殊的冗余状态是指将 a、b、c三相仅连接到直流侧的两个节点上的状态，例如状态220将三相仅连接到直流侧的2号和0号节点上。在状态220下，四个电容的电流分别为

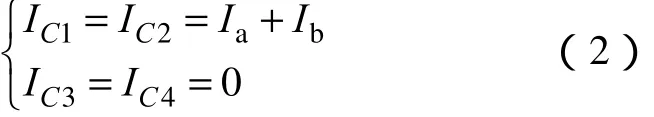
若有功电流Id＞0，则表示有能量输入逆变器，由于流经C3和C4的电流为零，因此能量都注入到C1和C2，此时必有IC1=IC2=Ia+Ib＞0；同理，若Id小于等于零，则有IC1=IC2=Ia+Ib≤0。

基于以上分析，可以推导当有功电流Id＞0时，8号三角形对应的电容电压的平衡算法，针对电压下降最多的电容进行讨论。

当电容C1的电压最低时，1号序列是最佳选择，因为在该序列下流经C1的电流都是正向电流Ia+Ib，因此电压负偏移最严重的电容C1将被注入尽可能多的能量，帮助其电压回归标准值。

当电容C2的电压最低时，由于流经C2的电流IC2此时有三种可能的取值即Ia+Ib、Ia和 0，因此不能直接做出最佳序列的判断，需要增设一个关于Ib的辅助条件来判定Ia+Ib和Ia的大小关系，分情况讨论如下：

（1）若Ib＜0，则有 0＜Ia+Ib＜Ia。结合表 1与表2可知，1号～4号序列在整个开关周期内都使得流经C2的电流为正向电流，并给C2充电、电压升高，其中1号序列还使得较大的正向电流Ia流经C2，因此是对C2最有利的开关序列，此时应考虑其他电容的电压偏移情况以及这四个可选序列对其他电容电压的影响。若当前电容C1的电压最高，则显然1号序列是不合适的，因为它在使C2充电的同时还使得C1在整个开关周期内都充电，进一步加大了C1的电压偏移程度；而4号序列既给C2充电，又不会将能量注入到C1，因此应采用4号序列进行调制。若当前电容C3的电压最高，则应选择1号序列，因为其既尽可能多地给C2充电，又尽可能少地给C3充电。同理，若当前C4的电压最高，也应选择1号序列进行调制。

（2）若Ib≥0，则有Ia+Ib＞Ia且Ia+Ib＞0。若当前电容C1的电压最高，则与（1）中的情况类似，应选取 4号序列。若当前电容C3的电压最高，则此时还需就Ia的方向进行讨论：若Ia是正向电流即Ia＞0，则有Ia+Ib＞Ia＞0，应选取 1号序列在使C2全周期充电的同时只传递最少的能量给C3；若Ia是反向电流，则应选取 2号序列，因为它在使C2最大程度充电的同时还使C3通过反向电流Ia放电。同理，若当前C4的电压最高，也需判断Ia的方向：若Ia是正向电流则选择2号序列，若Ia是反向电流则选4号序列。

当电容C3或C4的电压最低时可进行类似的推导来分析序列选择的条件，具体的判断规则在表 3中予以了总结。类似的，可以推导出当有功电流Id≤0时，8号三角形对应的电容电压的平衡算法以及第1扇区其他三角形对应的电压平衡算法，具体的推导过程不再累述。在五电平DCI的实时调制中，只要先检测四个电容的电压和相电流Ia与Ib的方向，然后应用表3中的规则对检测结果进行判断，即可确定适合的开关序列。由此可见，本文的算法在调制时只需要进行简单地比较运算而不涉及任何的四则运算，因而与基于能量函数的平衡算法和虚拟空间矢量算法相比，能够大大地减小实时运算量，提高计算效率。

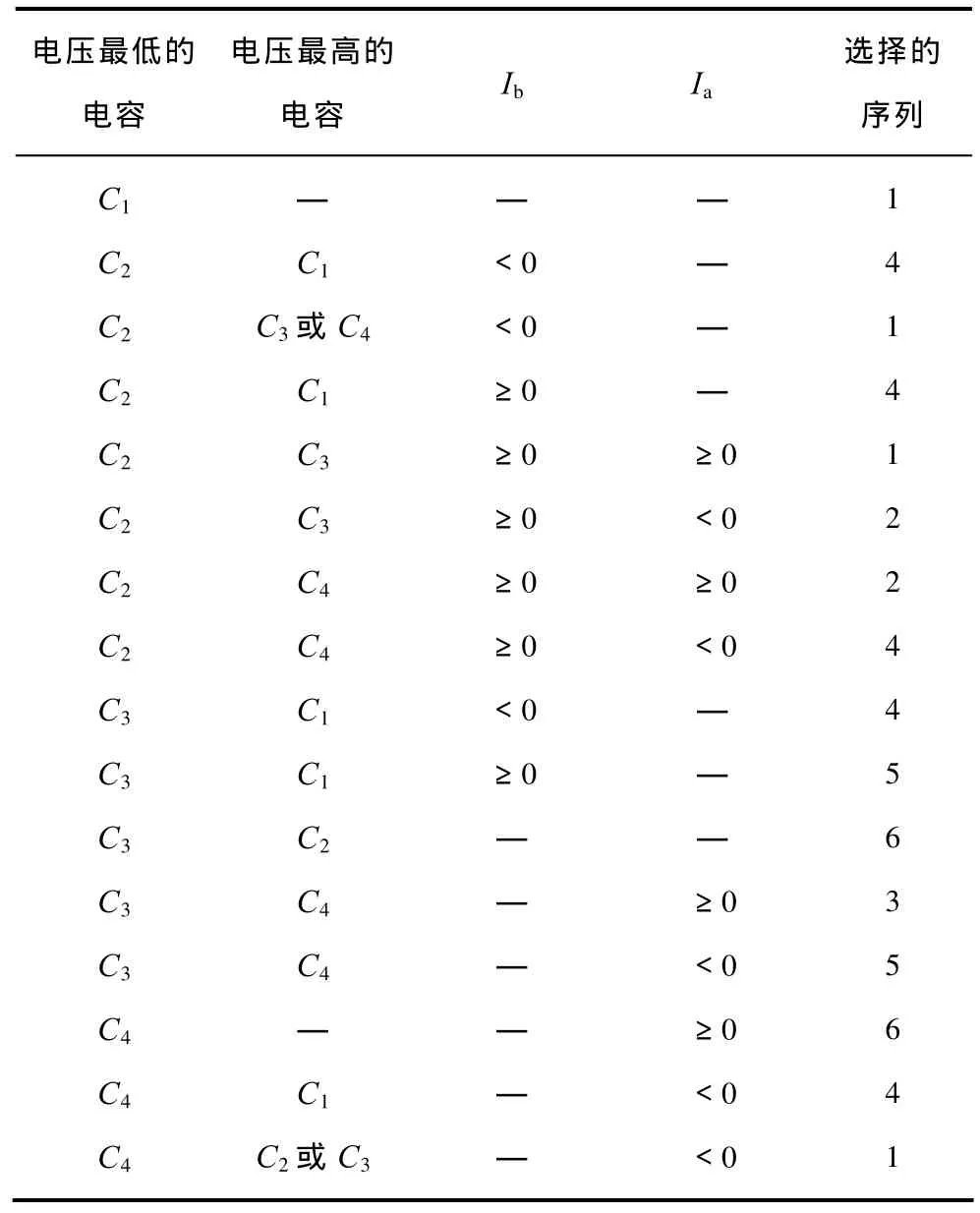
表3 Id＞0时第1扇区8号三角形开关序列的选择规则Tab.3 Sequence selection rules for triangle 8 in sector I when Id＞0

通过平衡算法选择了开关序列之后，调制的最后一步是为五段开关序列的每一段确定执行时间，从而为逆变器提供开关脉冲信号。根据计算得到NTV的作用时间和所选开关序列中三个空间矢量的排列顺序，很容易地确定每段的执行时间。观察表1可知，一个三角形对应的一组开关序列有三种不同的空间矢量排列顺序，对这三种情况应加以区别。图3显示有向上和向下的两类三角形，为了表示开关矢量的排列顺序，需要对这两类三角形的顶点进行编号，具体的编号方式如图4所示，在此基础上表4给出了开关序列类型的定义。作为一个例子，表1给出了第1扇区8号三角形对应的所有开关序列的类型。由于有了三角形顶点的编号方法，对向上和向下两类三角形的序列类型的定义可以统一起来（见表4），换句话说，在确定序列每段的执行时间时不必考虑三角形的类型了。由此，在选定了一个开关序列后，只要按照它的类型将NTV的作用时间分配给每一段即可。例如，若平衡算法选择的是 8号三角形的 1号序列，则按照它的类型（V2-V3-V1-V3-V2）可确定第1～第五段的执行时间分别为：T2/2、T3/2、T1、T3/2和T2/2，其中T1、T2、T3分别为 8号三角形的三个空间矢量V1、V2、V3的作用时间。

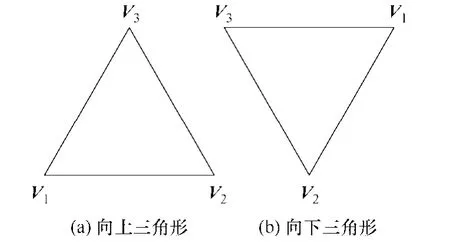
图4 最近三矢量的编号Fig.4 Numbering of the NTVs

表4 开关类型的定义Tab.4 Definition of the three sequence types

3.3 其他扇区的电压平衡算法

在第1扇区和其他五个扇区之间存在有两类对应关系，利用它们可以方便地从第1扇区的平衡算法出发得到其他五个扇区的算法。一类关系是第 1扇区与奇数号扇区，即第3扇区和第5扇区之间的关系，另一类是第1扇区与偶数号扇区，即第2扇区、第4扇区和第6扇区之间的关系。

（1）奇数号扇区的电压平衡算法。要找出第1和第3扇区之间存在的对应关系，关键是找出电流的对应关系，这可通过分析有功电流得到。有功电流Id是由五电平DCI的三相电流Ia、Ib和Ic通过派克变换得到的，当使Id从第1扇区对应到第3扇区时，它将逆时针旋转 120°，则三相电流Ia、Ib和Ic的轴线也将逆时针旋转120°，从而分别转到派克变换的b轴、c轴和a轴上（见图2）。因此，从第1扇区到第3扇区的电流对应关系是将Ia换成Ib、Ib换成Ic、Ic换成Ia，例如，在第3扇区8号三角形的状态 022（V3）下四个电容的电流可通过变换关系式（2）得到

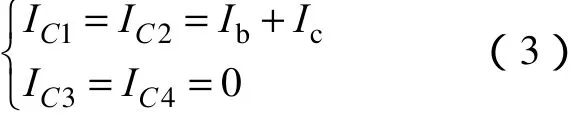
基于以上的分析，可通过两个步骤就方便地得到第3扇区的电压平衡算法：首先把第1扇区中一个三角形例如8号三角形的算法拷贝给第3扇区对应的三角形也即8号三角形，然后根据上述对应关系轮换算法中的电流变量即可，扇区间的三相变量对应关系在表5中进行了总结。

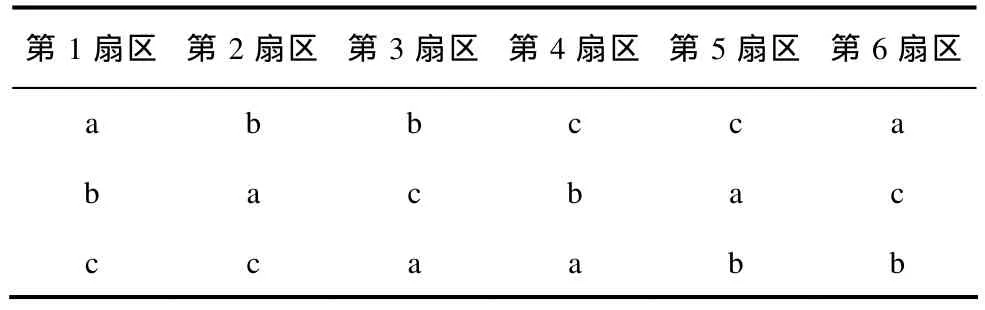
表5 扇区间三相变量的对应关系Tab.5 Phase variable mapping relations among sectors

两个扇区之间三相变量的替换关系同时也体现在开关状态的结构上，对比分属第1扇区和第3扇区的8号三角形的三个空间矢量：第1扇区8号三角形：V1（320, 431）、V2（210, 321, 432）、V3（220,331, 442）；第 3扇区8号三角形：V1（032, 143）、V2（021, 132, 243）、V3（022, 133, 244）。可见，第3扇区中的任一个开关状态是由它在第 1扇区中对应的状态经过表5所示的轮换关系得到的。

需要注意的是，六个扇区中所有的开关序列集都是按照下面两个规则编排顺序的：① 1号序列从三相电平都最低的那个序列开始，如表1中8号三角形的1号序列是从状态210开始的，在8号三角形对应的所有开关状态中，210的三相电平都是最低的； ②其他序列都是从它的前一序列的第二个状态开始。这样编排的好处是，对于两个扇区的两个对应三角形，如第1扇区的8号三角形和第3扇区的8号三角形，序号相同的序列其构成状态也是彼此对应的，因此在由第1扇区的算法构造第3扇区的算法时，不需要对开关序列号作任何修改。

第5扇区中各三角形的算法可用类似的步骤得到，只是由于 a、b、c三相的轴线是顺时针旋转，因此三相变量的替换关系是将Ia换成Ic、Ib换成Ia、Ic换成Ib，见表5。

（2）偶数号扇区的电压平衡算法。第1扇区与偶数号扇区之间的对应关系可通过它与第2扇区间的关系分析取得。当Id从第1扇区对应到第2扇区时，它将旋转60°，旋转后a、b、c三相的轴线与旋转前并不重合，因此第2扇区的算法不能通过直接轮换三相变量的方式得到。但观察图2可见，第1扇区与第2扇区关于派克变换的c轴呈镜像对称，例如第2扇区的6号三角形与第1扇区的8号三角形镜像对称，第2扇区的空间矢量（130, 241）与第1扇区的空间矢量（310, 421）镜像对称。通过这一观察结果可分析得到第2扇区算法的构造步骤：首先把第1扇区中一个三角形例如8号三角形的算法复制给第2扇区镜像对称的三角形也即6号三角形，然后将a相与b相电流变量互换并保持c相电流变量不变即可。

第1扇区与第2扇区相对应的开关状态之间也存在有类似的联系，对比第1扇区的8号三角形与第2扇区的6号三角形的空间矢量：第1扇区8号三角形：V1（320, 431）,V2（210, 321, 432）,V3（220,331, 442）；第 2扇区 6号三角形：V1（230, 341）,V3（120, 231, 342）,V2（220, 331, 442）。可见，将第1扇区的一个开关状态的a、b两相互换并保持c相不变，即可得到与它呈镜像对称的第2扇区的开关状态。同时，第1扇区8号三角形的空间矢量V2、V3分别与第 2扇区 6号三角形的空间矢量V3、V2呈镜像对称关系，这一关系也存在于两扇区中其他呈镜像对称的三角形之间。这种空间矢量的对应关系改变了第2扇区开关序列中V2与V3的排列顺序，如第1扇区8号三角形的1号开关序列为210（V2）-220（V3）-320（V1）-220（V3）-210（V2），而第2扇区6号三角形的1号开关序列为120（V3）-220（V2）-230（V1）-220（V2）-120（V3）。表 4对开关序列类型的定义考虑到了奇、偶数号扇区开关序列中空间矢量排列顺序的不同并进行了统一的定义，因此在构造偶数号扇区算法时不需要修改开关序列的序号和类型。

第4和第6扇区分别与第1扇区就派克变换的b轴和 a轴呈镜像对称关系，它们的电压平衡算法可由前述的方法和步骤得到，在此不再累述，三相变量的对应关系可参见表5。

4 仿真对比分析

本节在与基于能量函数的电压平衡算法进行比较的基础上，评估了本文提出的基于有功电流平衡算法的性能。基于能量函数的算法利用一个二次能量函数计算在当前所有可选开关状态下传输给所有电容的总能量，从而在NTV中各选出一个开关状态合成参考电压，使得当前开关周期内传输给电容的总能量最小[10,11]。

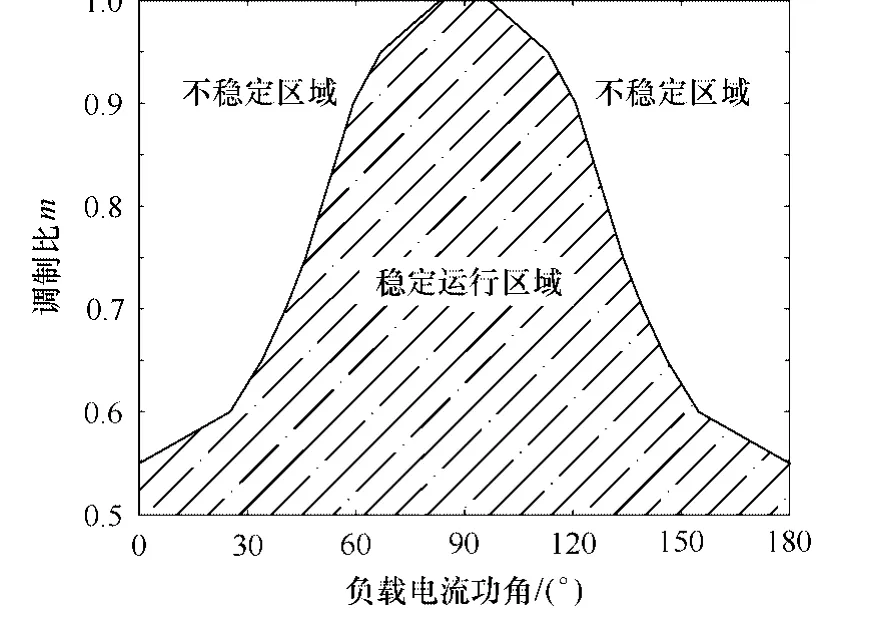
图5 五电平DCI在本文算法下的稳定运行区域Fig.5 Stability boundaries of the proposed scheme for a five-level DCI

DCMLI的SVM算法都使其运行受到交流侧功率因数和调制比的限制，只能在一定的区域内稳定工作[16-17]，本文所提算法也不例外。为此，本文对所提算法在多组功率因数和调制比取值下进行了仿真研究，获得了五电平DCI在本文算法下的稳定工作区域，如图5所示。从图上可见，本文算法与基于能量函数的 SVM 算法一样不适合于有较大有功功率交换的应用，但可用于进行无功补偿。因此，两种算法的仿真比较是在五电平DCI交流侧功率因数等于 0.3的情况下进行的，这是 DCI作为STATCOM（static synchronous compensator）运行时典型的功率因数值。在Matlab/Simulation中仿真的主要参数设置如下：C=1 000μF，f=60Hz，Vdc=8kV，fs=2 880Hz。对于以下所有的仿真实验，DCI直流侧四个电容的初始电压均设定为：VC1=2 200V，VC2=1 900V，VC3=2 100V，VC4=1 800V。两种算法的比较是在完全相同的仿真实验条件下进行的，以确保取得公平有效的比较结果。

首先比较的是五电平DCI在两种算法下的开关频率。由于五电平DCI有 24个开关器件且它们运行时的开关频率并不完全相同，因此本文定义了平均开关频率的概念

式中，fi是五电平DCI中第i个开关器件的频率。

基于能量函数的算法也采用五段式开关序列，同时还对开关序列进行了优化，以尽量减小开关频率。例如，若算法为当前开关周期选定的三个最佳冗余状态为310、200和321，则由它们构成的开关序列为200-310-321-310-200，因为这一排列顺序所引起的开关切换次数最少。表6是两种算法在功率因数为 0.3且调制比分别为 0.9、0.55和 0.3时五电平DCI开关频率的比较结果，从中可见本文算法在开关频率的指标上明显优于基于能量函数的算法。同时可见当调制比较小时这一优势更加明显，这是因为当调制比较小时，可用来合成参考电压矢量的冗余状态就更多，基于能量函数的算法选择电平跨度大的冗余状态的机会就会增大，导致开关频率随之增大。

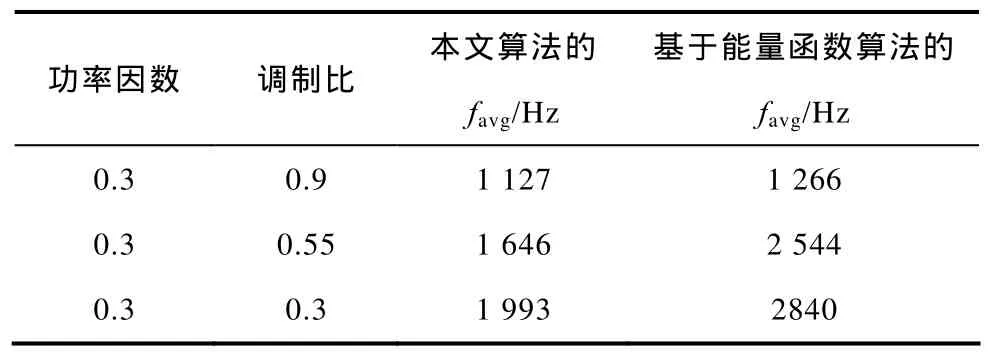
表6 两种算法开关频率的比较Tab.6 Comparison on switching frequency of the two schemes

其次对比了两种算法的计算量。表7是两种算法在任一扇区的16个三角形中或者说在16组NTV下产生最佳开关序列所需要的运算次数，其中对于基于能量的算法只计及乘法的次数而省略了加法次数。从表中可见本文算法可大大降低计算量，因而在同等硬件实现条件下势必具有更高的运算效率。

表7 两种算法运算量的比较Tab.7 Comparison on operation volume of the two schemes

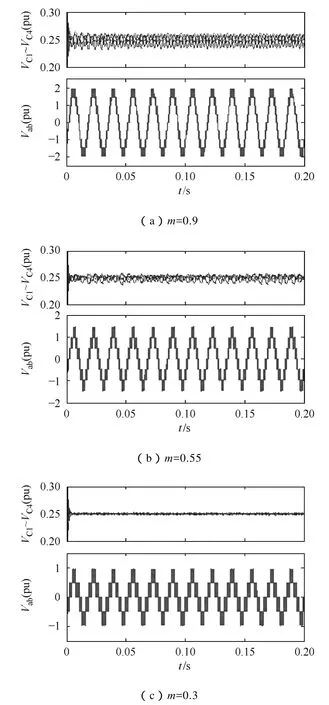
图6 五电平DCI在功率因数为0.3的对称负载下的仿真结果Fig.6 Simulation results of the proposed scheme with a balanced sinusoidal load of 0.3 PF

随后给出了本文算法在不同工况下的四个电容电压VC1～VC4和输出线电压Vab的波形。图6是五电平DCI在不同调制比下接三相对称正弦负载时的图形，由图可见四个电容的电压从初始的偏移状态达到了平衡状态，且线电压的波形在调制比分别为0.9、0.55和0.3时显示为典型的9级、7级和5级阶梯形状。图7显示的是本文算法分别在不对称负载和谐波畸变负载下的性能。图 7a是五电平 DCI在不对称负载下的运行结果，逆变器交流侧三相电流的幅值分别是200A、230A和150A；图7b是当逆变器交流侧电流中注入5%的5次谐波和8%的7次谐波的结果，波形图表明本文算法在不对称负载和畸变负载下亦能很好地平衡电容电压。

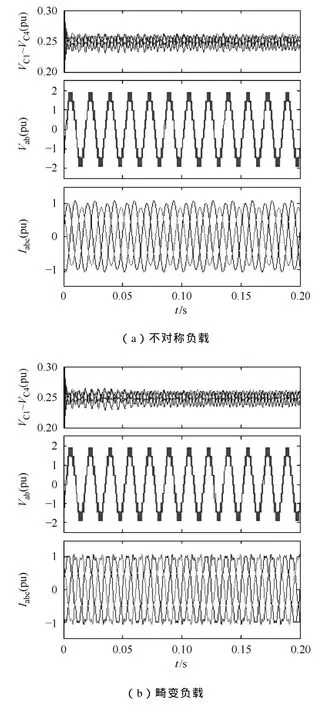
图7 五电平DCI在不对称负载和谐波畸变负载下的仿真结果Fig.7 Simulation results of the proposed scheme with an unbalanced load and a distorted load respectively

最后，考虑到实际电容的大小总是与其标称值之间存在一定的误差以及标称值相同的电容实际损耗可能不同的情况分别进行了仿真实验。图8a是将电容C1～C4的大小分别浮动-9%、+10%、-5%、+6%来模拟实际电容误差情况的电容电压仿真结果。图 8b是将四个阻值分别为 0.4Ω、0.2Ω、0.3Ω和 0.5Ω的电阻分别与电容C1～C4串联来模拟这四个电容不同损耗情况的仿真结果。两个仿真实验都是在调制比为0.9、功率因数为0.3的条件下进行的。仿真结果表明本文所提算法在电容存在误差和电容损耗不同的情况下均能使得电容电压从初始的偏移值出发维持在了平衡状态。

图8 考虑实际电容参数情况的仿真分析结果Fig.8 Simulation results of the proposed scheme considering the characteristics of actual capacitors

5 结论

本文提出了一种不需借助任何辅助电路或独立电源的空间矢量调制算法来实现五电平DCI的直流侧电容电压平衡。算法利用有功电流来判断DCI交流侧的能量传输方向，通过分析能量传输方向与不同的开关序列对电容电压的影响，算法从一组预定义的开关序列中选取使得偏离标准值最多的电容电压尽可能回归的开关序列。该算法在实时调制中只需要通过比较运算来选择最佳开关序列而不需要进行任何四则运算，因而能有效减小运算量，提高算法效率。除此之外，本文算法通过对开关序列的组织实现了开关频率优化，跟现有的基于能量函数的算法相比显著降低了DCI的开关频率，从而能有效降低开关损耗。仿真分析同时表明，本文算法在不对称和谐波畸变等负载条件下以及电容值存在误差和电容损耗不一致的情况下仍能实现电容电压的平衡。尽管DCMLI的SVM算法受到运行区域的局限，但本文算法对于DCMLI作为STATCOM的应用仍是非常适合的。

[1] Celanovic N, Boroyevich D. A comprehensive study of neutral-point voltage balancing problem in three-level neutral-point-clamped voltage source PWM inverters[J]. IEEE Transactions on Power Electronics, 2000, 15(2): 242-249.

[2] Saengseethong A, Sangwongwanich S. A new modulation strategy for capacitor voltage balancing in three-level NPC inverters based on matrix converter theory[C]. Proceedings of the 2010 International Power Electronics Conference, 2010: 2358-2365.

[3] Yazdani A,Iravani R. An accurate model for the DC-side voltage control of the neutral point diode clamped converter[J]. IEEE Transactions on Power Delivery, 2006, 21(1): 185-193.

[4] 赵辉, 李瑞, 王红君, 等. 60°坐标系下三电平逆变器 SVPWM 方法的研究[J]. 中国电机工程学报,2008, 28(24): 39-45.Zhao Hui, Li Rui, Wang Hongjun, et al. Study on SVPWM method based on 60° coordinate system for three-level inverter[J]. Proceedings of the CSEE,2008, 28(24): 39-45.

[5] Menzies R W, Steimer P, Steinke J K. Five-level GTO inverters for large induction motor drives[J]. IEEE Transactions on Industry Applications, 1994, 30(4):938-944.

[6] Hasegawa K, Akagi H. A new DC-voltage-balancing circuit including a single coupled inductor for a five-level diode-clamped PWM inverter[J]. IEEE Transactions on Industry Applications, 2011, 47(2):841-852.

[7] Shukla A, Ghosh A, Joshi A. Flying-capacitor-based chopper circuit for DC capacitor voltage balancing in diode-clamped multilevel inverter[J]. IEEE Transactions on Industrial Electronics, 2010, 57(7): 2249-2261.

[8] 洪春梅, 王广柱. 五电平逆变器直流侧电容电压的平衡与控制[J]. 电机与控制学报, 2003, 7(3): 202-206.Hong Chunmei, Wang Guangzhu. DC bus voltage balancing and control in five-level inverters[J].Electric Machines and Control, 2003, 7(3): 202-206.

[9] Pou J, Pindado R, Boroyevich D. Voltage-balance limits in four-level diode-clamped converters with passive front ends[J]. IEEE Transactions on Industrial Electronics, 2005, 52(1): 190-196.

[10] Saeedifard M, Iravani R, Pou J. Analysis and control of DC-capacitor-voltage-drift phenomenon of a passive front-end five-level converter[J]. IEEE Transactions on Industrial Electronics, 2007, 54(6):3255-3266.

[11] Khajehoddin S A, Bakhshai A, Jain P K. A simple voltage balancing scheme for m-level diode-clamped multilevel converters based on a generalized current flow model[J]. IEEE Transactions on Power Electronics,2008, 23(5): 2248-2259.

[12] Busquets Monge S, Alepuz S, Rocabert J,et al.Pulsewidth modulations for the comprehensive capacitor voltage balance ofn-level three-leg diodeclamped converters[J]. IEEE Transactions on Power Electronics, 2009, 24(5): 1364-1375.

[13] 李国丽, 史晓锋, 姜卫东, 等. 二极管钳位型多电平逆变器脉宽调制时电容电压均衡方法[J]. 电工技术学报, 2009, 24(7): 110-119.Li Guoli, Shi Xiaofeng, Jiang Weidong, et al.Unbalancing capacitor voltage for diode clamped multi-level inverter[J]. Transactions of China Electrotechnical Society, 2009, 24(7): 110-119.

[14] Wu B. High-power converters and AC drives[M].New Jersey: Wiley & IEEE Press, 2006.

[15] Bakhshai A R, Rad H R S, Joos G. Space vector modulation based on classification method in three-phase multi-level voltage source inverters[C].Proceedings of IEEE Institute for Advanced Studies,2001: 597-602.

[16] Marchesoni M, Tenca P. Theoretical and practical limits in multilevel MPC inverters with passive front ends[C]. Proceedings of 9th European Conference on Power Electronics (EPE), 2001: 1-12.

[17] 高跃, 李永东. 二极管钳位型五电平逆变器电容电压平衡域研究[J]. 电工技术学报, 2008, 23(1): 77-83.Gao Yue, Li Yongdong. Voltage balance boundary of five-level diode clamped inverters[J]. Transactions of China Electrotechnical Society, 2008, 23(1): 77-83.