支持向量机和B P神经网络在水轮发电机轴承故障诊断中的应用

张锋利，陈文献，贾海英

（1.陕西地方电力设计有限公司，陕西西安 710065；2.安康供电局，陕西安康 725000；3.广东技术师范学院天河学院，广东广州 510540）

支持向量机是Cortes和Vapnik在1995年首先提出的，它是以统计学理论为基础专门研究小样本情况下的机器学习方法，在解决小样本、非线性及高维模式识别中表现出许多特有的优势[1]。支持向量机以训练误差为主要的优化约束条件，以置信范围最小化作为优化最终目标，可以应用到数据的分类和回归。BP神经网络是一种模拟人脑中神经元之间在对问题做决定的过程。也是一种常用的模式识别和信号处理的工具，它一般是由3层前馈型网络构成，结构简单，作为一种自适应的模式识别技术，神经网络具有很好的适应能力和学习能力，但存在容易陷入局部极值的问题。目前的研究中对支持向量机和BP神经网络在模式识别应用中的性能比较较少。本文通过对滚动轴承的故障特征量在支持向量机和BP神经网络中作故障模式识别的比较，来比较在小样本集上支持向量机和BP神经网络的逼近能力以及泛化能力。

水轮发电机滚动轴承广泛应用于各种卧式水轮机当中。由于经常会受到交变载荷反复作用，轴承会不断承受剧烈变化的碰撞，随着机组运行时间的不断增加而产生疲劳损伤。当主轴和轴承在运动过程中，主轴会周期性的撞击轴承的故障部位，产生冲击力，从而会激励轴承座产生共振，形成周期循环的冲击振动。这些冲击振动的信号是非线性、非平稳的振动信号。要诊断轴承故障的首要任务就是要从这些非平稳信号中提取出故障特征向量[2]。

本文采用的经验模态分解（简称EMD）来自Hilbert-Huang变换中的Huang变换[3]，是由美国华裔科学家Norden E.Huang在1998年提出的一种对非线性、非平稳信号非常有效的一种处理方法[4]。EMD分解方法可以将混杂各种频率的原始信号直接分解为若干个从高频到低频分布的固有模态函数（简称IMF）。

本文采用支持向量机和神经网络对经验模态分解得到的轴承故障特征量进行训练和故障识别，对支持向量机和BP神经网络进行对比分析。

1 基于EMD的特征值提取

经验模态分解（EMD）克服了快速傅里叶变换在处理非线性、非平稳性信号中的不足[5]。从理论中来说，EMD是对非平稳信号进行平稳化处理，利用局部特征时间的尺度，将原始信号中混杂这不同频率的波动逐级提取出来，得到一系列不同特征尺度的数据序列。这些序列被称作固有模态函数IMF（Intrinsic Mode Function）以及一个残余分量，每一个IMF都含有不同的频率成分，其阶数越低，其波形的频率越高，体现了原始数据中的局部特征。其每个IMF都满足以下两个特点：①在整个波形序列中，极值点的数目和波形与零点交叉点的数目相等，或最多相差一个；②在波形中的任何一点，由最大值点形成的上包络线与最小值点形成的下包络线均值须为零。对提取出的每个IMF分量作进一步的运算，本文中采用求各IMF的总能量E，可以得到原始信号的特征信息。最后再将这些特征量输入到神经网络或支持向量机进行训练，从而实现轴承的故障诊断。

EMD算法由以下几个步骤组成[6]：

1）找出原始信号的所有局部极大值点以及局部极小值点，然后将这些极值点分别用三次样条函数进行拟合，得到原始信号x（t）的上包络线和下包络线，并计算上下包络线的均值并循序连接得到。上下包络线均值曲线记为m1（t）。

2）用原信号序列x（t）减去均值线m1（t）得到

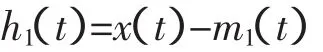
判断h1（t）是不是固有模态函数，即是否满足固有模态函数的两个条件。如果不是，则把h1（t）作为原函数重复上述步骤，知道第k次得到的hk（t）是一个固有模态函数为止。记作c1（t）

3）由上述步骤分解得到的第一个固有模态函数c（1t），然后计算剩余信号得到

4）把r1（t）作为新的原始信号重复以上分离过程，得到所有的固有模态函数rj（t）

5）通过以上分解原始信号被分解为个IMF分量及一个n阶残差rn（t）之和

通过以上的EMD分解过程，包含着混叠频率的原始信号就分解出了n个ci（t）分量，其中阶次越小的IMF分量所包含的频率成分越高。所以，原始信号的主要信息都是包含在前几个分量中。因此在后面的提取特征向量的计算中只选取前几个分量进行计算[7]。

2 诊断方法

2.1 BP神经网络

神经网络是通过对已知输入数据的不断训练，从而调整整个网络的权值，使满足精度条件的网络具备模式识别的功能。目前应用于故障诊断的神经网络多采用误差反向传播的BP神经网络，该网络的权值调整规则采用由后向前不断传播，以使其达到规定的输出误差精度[8]。BP神经网络一般由一个输入层、一个或多个隐含层以及一个输出层组成，每层均包含若干神经元[9]。

隐含层中神经元输入函数为

式中，x1，…，xn为输入的训练数据；wji为神经元之间的连接权值，θi为神经元的阈值；隐层神经元输出函数为f（ui）（i=1，2，…，q），f（ui）通常使用sigmod函数。

输出层函数为

式中，wjk表示输出层神经元之间的连接权值。

通过给以上网络输入数据进行训练，不断求得网络输出与期望输出之间的误差，再通过计算局部梯度来修正网络权值，直到所得误差符合预定目标，从而使训练后的网络具备对新输入数据进行准确分类的功能[10]。但是，BP网络也存在收敛速度慢，容易陷入局部极小的缺点。

2.2 支持向量机

支持向量机SVM实现的基本思想是通过事先选择好的某一个非线性变换，将输入向量由低维样本空间映射到高维或无穷维的特征样本空间[11]。在这一样本空间中构造一个最优分类超平面。

在考虑非线性映射方面，即x圯准（x），准函数即内积核函数的是否存在，可由Mercer定理得到保证。通过样本空间的非线性变换得到的线性样本空间之后，SVM就可以通过求解最优解的方法来寻找最优划分超平面的支持向量[12]。

SVM的工作就是要找到分类面两边的向量使样本分开并且达到间隔最大化。

最优超平面推导过程如下：设训练样本{xi，yi}Ni=1，其中xi是输入样本，yi是待分类的两个类别。

分类超平面可用以下方程表示

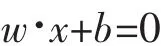
式中，w是超平面的法向量；b是超平面的常数项。

现在寻找最优超平面，也就是寻找最优w和b。两类待分的样本都满足|w·x+b|≥1，因此|w·x+b|=1，就是离分类平面最近的样本点。这样，问题就可归纳为求

寻找最优超平面也就最终归结为一个二次规划问题[13]。

3 故障诊断仿真研究

水轮发电机滚动轴承疲劳损伤主要是在内圈和外圈表面点蚀、裂纹，以及滚动体失圆、滚道产生压痕[14]。本文采取美国西储大学轴承实验室提供的滚动轴承故障数据。本次试验选取的故障数据包括轴承正常以及内圈、外圈和滚动体上的故障数据。内圈、外圈和滚动体上的故障均是人为通过电火花加工技术布置的单点故障，故障点直径分别为0.007、0.014、0.021 in（1 in=2.54 cm下同）。数据的采样频率为12000 Hz，在轴承转速为1797 r/min下采集了10 s的数据。

在确定试验诊断数据之后，开始进行故障特征向量的提取。本实验提取故障特征向量采用前文叙述过的经验模态分解EMD。由于EMD分解中在用3次样条插值进行包络线拟合时容易产生端点飞翼现象，而解决此问题多采用端点延拓方法，但考虑轴承振动数据量大等特点采用将波形边界点归为极值点来进行拟合处理，可以达到解决端点飞翼现象的问题。下面以内圈在转速为1797 r/min故障点直径为0.007 in的数据为例，来进行故障特征向量提取。图1为采集时间为一秒内振动的原始信号。

图1 原始振动信号Fig.1 The original vibration signal

用EMD进行分解得到12个IMF及一个余项，考虑原始信号的信息主要包含在前几个分量中，于是选取前8个分量进行特征向量提取[15]，分解图形如图2所示。

得到IMF分量后，选择各IMF的平均能量作为故障特征向量，其计算公式为

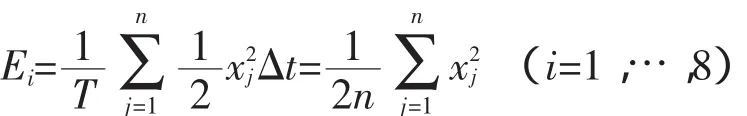
式中，x为波形的振幅，n为采样点数。再经过归一化后，特征向量为

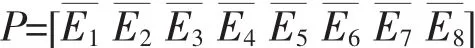
图2EMD分解后的前8个IMF分量Fig.2 The first eight IMF components after EMD decomposition

进过计算后得到的特征向量如表1所示。

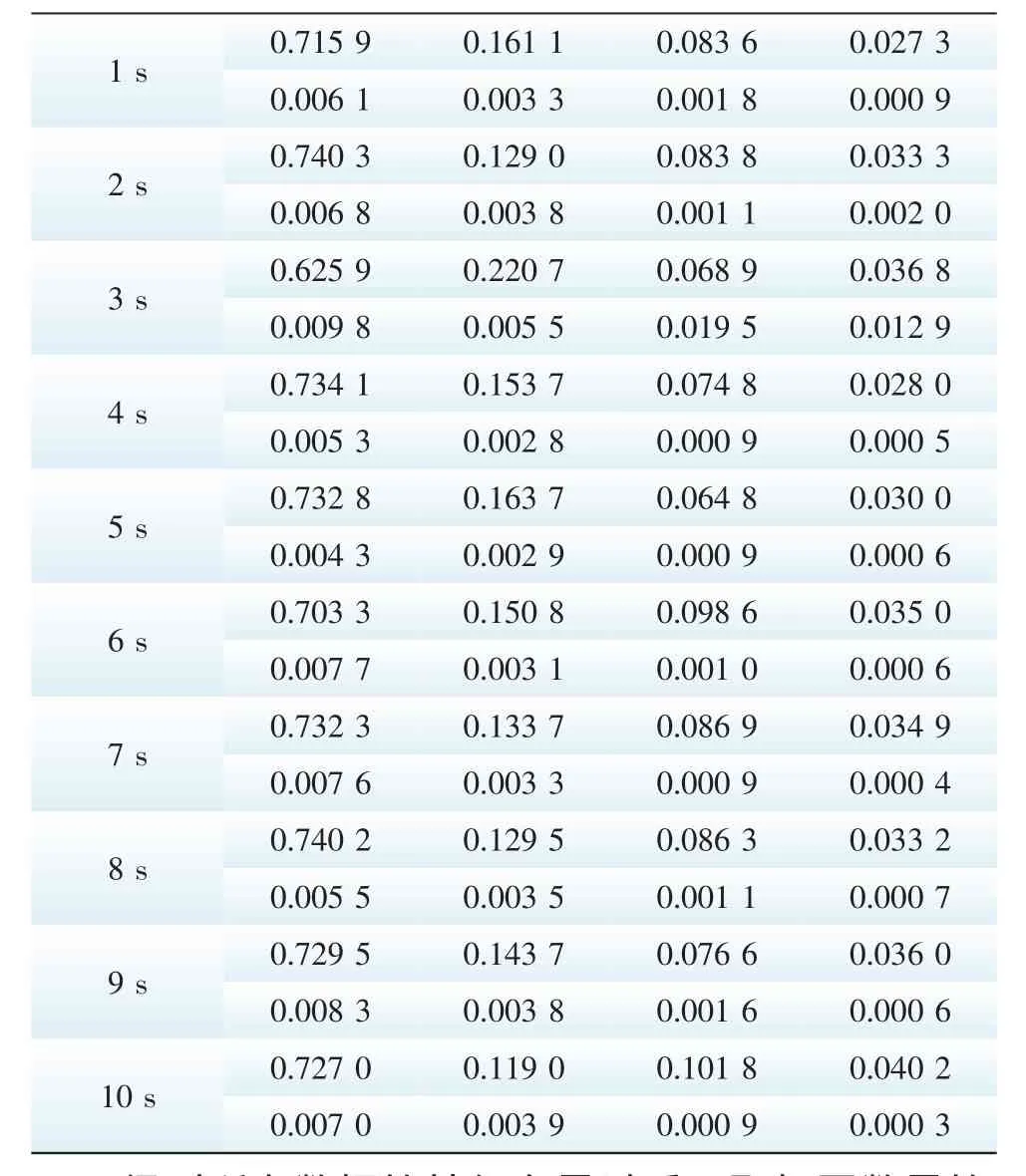
表1 10 s故障特征向量Tab.1 10 s fault feature vectors

得到所有数据的特征向量以后，取相同数量的特征向量分别输入到支持向量机和BP神经网络进行训练，再将训练好的网络输入相同数量的测试值来进行诊断，在考虑使用BP神经网络可能会陷入局部极值的问题[16]，采用了遗传算法优化后的BP神经网络，这里对其优化算法不在具体阐述。试验得到的对比结果表2所示。

表2 诊断准确度结果对比Tab.2 Comparison of the diagnostics accuracy results

通过表2的结果计算准确度之间的均方根误差可得：支持向量机方法的均方根误差为0.0115；而BP神经网络的均方根误差为0.0529；可见BP神经网络受样本训练数目影响很大，而支持向量机受到样本数的影响却较小。从准确度的比较中可以看出SVM在小样本故障诊断中的准确度要高于BP神经网络的准确度。

4 结语

支持向量机和BP神经网络在水轮发电机滚动轴承诊断中得出的结果可以看出，支持向量机的逼近能力比BP神经网络的逼近能力更具优势。当训练样本变化时，虽然支持向量机与BP神经网络的准确度均有变化，但是支持向量机准确度的变化幅度小于BP神经网络的变化幅度。而且，支持向量机的准确度也是高于BP神经网络，可见在小样本学习中支持向量机有较好反应数据变化趋势的能力。因此，在选用水轮发电机滚动轴承故障诊断方法中可优先考虑使用支持向量机作为故障诊断的模型。

[1] 阎辉，张学工，李彦达.支持向量机与最小二乘法的关系研究[J].清华大学学报，2001，41（9）:77-80.YAN Hui，ZHANG Xue-gong，LI Yan-da.Relation between a SVM and the least square method[J].Journal of Tsinghua University，2001，41（9）:77-80（in Chinese）.

[2] 张贤达，保铮.非平稳信号分析与处理[M].北京：国防工业大学出版社，1991.

[3] 杨宇，于德介，程军圣.基于Hilbert-Huang变换的特征量法及其在滚动轴承故障诊断中的应用[J].计算机工程及应用，2004，28（2）:26-33.YANG Yu，YU De-jie，CHENG Jun-sheng.The feature energy method based on hilbert-huang transform and its application to roller bearing fault diagnosis computer[J].Engineering and Applications，2004，28 （2）:26-33（in Chinese）.

[4]HUANG N E，SHEN Z，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear nonstationary time series analysis[J].Proceeding of the Royal society，1988，454（1971）:903-995（in Chinese）.

[5] 卢艳军，刘颖，国凤娟.基于经验模态分解与支持向量机的旋转机械碰磨故障识别方法研究[J].制造业自动化，2010，32（12）:7-10.LU Yan-jun，LIU Ying，GUO Feng-juan.Study on rub and impact fault of rotating machinery identification method based on EMD and SVM[J].Manufacturing Automation，2010，32（12）:7-10（in Chinese）.

[6] 杨勇.EMD和模糊神经网络在滚动轴承故障诊断中的研究和应用[D].太原：太原理工大学，2008.

[7] 罗奇峰，石春香.Hilbert-Huang变换理论及其计算中的问题[J].同济大学学报，2003，31（6）:637-640.LUO Qi-feng，SHI Chun-xiang.Hilbrt-Huang transform and several problems in its calculation method[J].Journal of Tongji University，2003，31（6）:637-640（in Chinese）.

[8] 陈向东，赵登峰.基于神经网络的滚动轴承故障检测[J].轴承，2003，23（2）:16-51.CHEN Xiang-dong，ZHAO Deng-feng.Diagnosis of rolling bearing based on neural network[J].Bearing，2003，23（2）:16-51（in Chinese）.

[9] 王丽，王红梅，吴振洲.基于神经网络和支持向量机的电能质量组合评价[J].华北水利水电学院学报，2009，30（3）:61-64.WANG Li，WANG Hong-mei，WU Zhen-zhou.Based on neural network and SVM power quality portfolio evaluation[J].Journal of North China Institute of Water Conservancy and Hydroelecrtic Power，2009，30（3）:61-64（in Chinese）.

[10]申东日，冯少辉，陈义俊.BP网络改进方法概述[J].化工自动化及仪表，2000，27（1）:13-16.SHEN Dong-ri，FENG Shao-hui，CHEN Yi-jun.Survey of improved method for BP network[J].Chemical Instrument and Automation，2000，27（1）:13-16（in Chinese）.

[11]赵海洋，王金东，刘树林，等.基于神经网络和支持向量机的复合故障诊断技术[J].流体机械，2008，36（1）:39-43.ZHAO Hai-yang，WANG Jing-dong，LI Shu-lin，et al.Compound fault diagnosis technique based on artifical neural network and SVM[J].Fluid Mechnics，2008，36（1）:39-43（in Chinese）.

[12]Vapnik V.The nature of statistical learning theory[M].New York:springer-verlag，1999（in Chinese）.

[13]Achmad widodo，Bo-suk young.Support vector machine in machine condition monitoring and fault diagnosis[J].Mechanical System and Signal Processing，2007，21（6）:2560-2574（in Chinese）.

[14]屈梁生，何正嘉.机械故障诊断学[M].上海:科学技术出版社，1986.

[15]胡倩.基于BP神经网络的滚动轴承缺陷诊断研究[D].武汉：华中科技大学，2006.

[16]丁福焰，邵军，张生玉，等.神经网络在滚动轴承故障诊断中的应用[J].振动工程学报，2004（17）：423-425.DING Fu-yan，SHAO Jun，ZHANG Sheng-yu，et al.Neural network in fault diagnosis of rolling bearing and application[J].Journal of Vibration Engineering，2004（17）：423-425（in Chinese）.